Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 2

Подождите немного. Документ загружается.

391

 



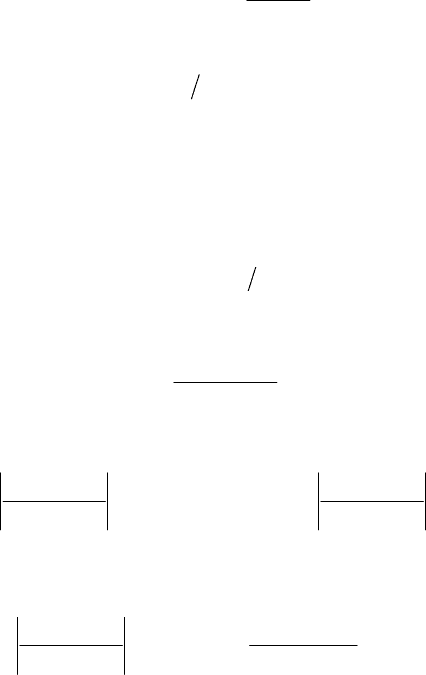
M T

d M

















. (12.65)

Поскольку в исходное уравнение движения системы

(12.62)

производные

d M dt

i i

 не входят, то они не войдут и

в приводимый ниже лагранжиан. Поэтому следует ожидать,

что экстремум функции







M t

может достигаться на раз-

рывной функции







M t

, скачком меняющий свое значение

(модуль) в любую сторону в двух противоположных направ-

лениях [432].

Следовательно, экстремум в неравенстве (12.64) будет

достигаться на границе









 

M t M t

c c

макс

 1 , т. е. где это

неравенство переходит в равенство:

 



M t

dt T

c макс

















. (12.66)

Действительно, если

 



M t

макс

 1, то при





 



M t

макс

  ;

если же наоборот, хотя на сколь угодно малом участке,

 



M t

макс

1 , то

 



M t

dt T

макс

















Таким образом, приходим к общей задаче Лагранжа [563]:

найти функции







M t

или







M t







M t

, доставляющие

максимум интегралу (12.65) при заданном уравнении связи

(12.62) и верхнем пределе области (12.66).

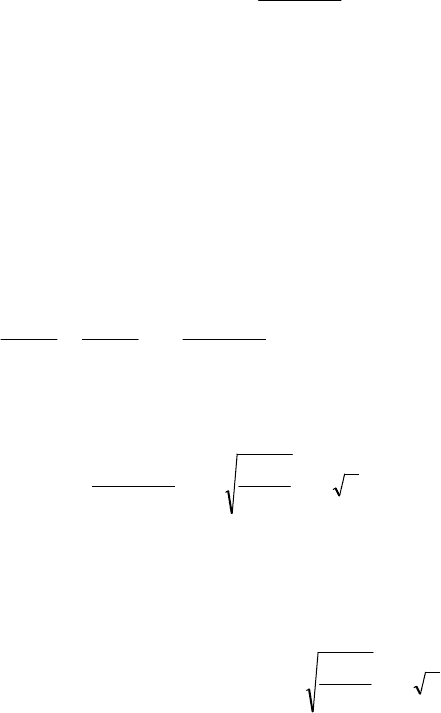
392

Искомые функции







M t







M t







M t

, должны

удовлетворять, как было упомянуто, двум уравнениям Эйле-

ра для промежуточной функции [469, 549]:

L p M

 

















12 0



макс









    

p p M M

012

12 02

2     . (12.67)

Здесь 

— постоянный множитель Лагранжа, определя-

ется при граничных условиях решения уравнения Эйлера для

функции 

;



—

множитель Лагранжа — независимая

функция от 

, определяется решением второго уравне-

ния Эйлера для функции







M t

Определим из (12.67) решение уравнения Эйлера для











 

M M

c c



































макс

из которого следует, что





M m

макс

 



2 1

2 

 .

Переходя к пределу, получим искомую функцию возму-

щения







 , доставляющую максимум упругому моменту

для принятого по (12.64) условия:

 

lim lim

c c

M M

 



  





макс

2 1

, (12.68)

393

но при





корень степени 2

т—

1 из любого числа равен

единице и совпадает по знаку с этим числом, т. е.



2 1





  , если





 и 

2 1



  , если    0 .

При любом соотношении параметров реальной системы

электропривода 

0 , так как не может быть отрицатель-

ного момента инерции или жесткости упругого вала, одно-

временно и 2 0

  , так как

и 

— положительные и

действительные величины. Поэтому сомножитель правой

части в (12.68)



2 1





  ,

следовательно, знак и модуль искомой функции 

по

(12.68) будет зависеть от единичной нелинейной функции

sign

при





 

 







1 0

;

и определяться выражением:





 

M M

c c

  

макс

sign . (12.69)

Решение (12.69) в явном виде находим после определения







по второму уравнению Эйлера:

   









i i

 

12 12

0 1 2













 , , .

Это уравнение для вспомогательной зависимости (12.67)

будет

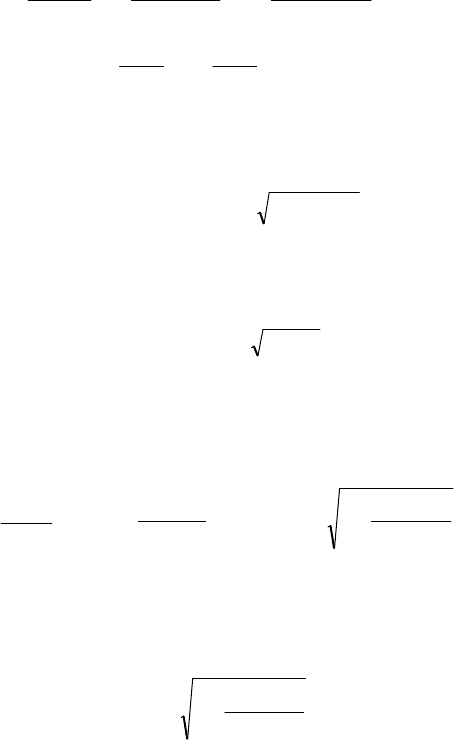
394

   







p M

  

 

     

1 2

012

 





  (12.70)

или





 

p p t

012

2 0    .

Корни этого уравнения

1 2

012

     указывают на

возможность двух характерных случаев опасного воздействия

динамической нагрузки на упругое звено системы электро-

привода с возрастанием по экспоненте.

Так, например, при слабом затухании в упругом элемен-

те, т. е. при   

012

(или

p c J

1 2 12



эк

), что наиболее ве-

роятно для рассматриваемой системы электропривода, ре-

шение







будем искать в виде

 





 



t Аe t

 sin 

где 





экв

;

J J

экв

1 2





;  

12 012

 



С J

экв

;





,  

— постоянные амплитуда и фаза







Следовательно,

 









t Ae

С J

 



























sin  

экв

и, соответственно,

395

 

  

M t M Ae

С J

c c

  















макс

экв





012

2 1

sin .

(12.71)

Воздействие на максимум искомой по (12.71) функции

возмущения двух первых сомножителей подкоренного ввиду

тождества lim







 



2 1

экв

исключается,

поэтому нали-

чие экспоненциального сомножителя в (12.71) с положитель-

ной степенью не приводит к возрастанию максимального

возмущающего воздействия на упругое звено. Это позволяет

упростить последнее выражение







M t

и получить оконча-

тельно

 

   

M t M

С J

c c

  













макс

экв

sign sin .

012



 (12.72)

Полученное значение







M t

указывает, что в общем

случае наиболее опасным динамическим воздействием на

упругий валопривод двухмассового агрегата с соединитель-

ной муфтой является кусочно-постоянное (несинусоидаль-

ное) воздействие со стороны механизма либо электродвига-

теля, меняющее знак через время

 

С J







1 4

экв

равное полупериоду собственных циклических колебаний ва-

лопривода с упругой муфтой.

При относительно большом затухании, когда   

012

(или



12 12

2

С J

экв

), переходная характеристика валопривода по

(12.71) имеет апериодический характер и относительно опасным

воздействием следует считать максимальную статическую на-

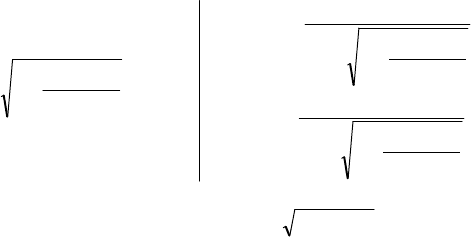
396

грузку механизма, вызывающую наибольшую деформацию (уп-

ругий момент) в упругом элементе (см. ниже).

Максимального значения упругого момента, приклады-

ваемого к выходному концу вала двигателя или к приемному

концу вала механизма, следует ожидать в случаях длительно-

го воздействия возмущающего момента





M t

определяемо-

го по (12.72). Для определения максимума упругого момента

(или момента деформации) найдем периодическое решение

(12.70) с учетом (12.72).

Исходное уравнение для отыскиваемого решения







M t

будет:





   





p p M t M t

012

2       

макс

sign sin , (12.73)

где

sign =

+1 при

-1 при

экв

sin

;



012

 

































С J

Решение уравнения (12.73) при 

4

С J

экв

равно сум-

ме его частного решения







M t

и общего решения







M t

соответствующего однородного уравнения (т. е





  

M t

0), представляющего периодическое решение.

Таким образом,













  

M t M t M t

12 12

  ,

или

 









   

M t А e t M t

12 1 02 1 02

   



 sin ,

макс

sign sin

(12.74)

где

, 

— соответственно амплитуда и фаза свободного

колебательного процесса по (12.74).

397

Значение этих постоянных определяем по начальным ус-

ловиям. При этом учитываем, что характер функции







M t

является кусочно-непрерывным при



, sign sin

  1 ;





 

M t M

c c



макс

Значения постоянных будут соответственно:

С J

12 12





экв



;





12 12





arctg

экв

С J

и, согласно (12.74), момент

 

  

M t M

С J

e t

12 12











 



макс

экв

sin













+ sign sin



 

. (12.75)

Это уравнение показывает, что наибольший упругий момент,

который имеет место при условии

С J











012

экв

определится по формуле

 

M M

С J

12 12

макс макс

экв















, (12.76)

а динамический коэффициент упругого вала привода

398

С J

экв

 



12 12





(12.77)

Для малых 

, т. е. 

12 12

2

С J

экв

, и следовательно,

при малом затухании энергии упругой деформации в вало-

проводе:

 

 



012

lim

M M

С J

макс макс

экв



Таким образом, получается, что при кусочно-постоянном

воздействии на упругий валопровод, находящимся в резо-

нансе с периодом свободных колебаний двухмассовой меха-

нической системы ( 

012

), наибольший упругий момент (или

упругая деформация 

12 макс

) в





С J

экв





раза пре-

восходит 

макс

, если бы это было статической нагрузкой.

Отметим, что при абсолютно жесткой конструкции со-

единительной муфты и валопривода в целом, т. е. при



0 , свободная составляющая упругого момента будет

изменяться по гармоническому закону со сдвинутой по фазе

на угол  2 радиан циклической частотой свободных коле-

баний этого валопровода ( 

012

) и с амплитудой 

макс

то время как воздействие принужденной составляющей ос-

танется неизменным, поэтому

 

   

M t M t t

12 012 012

 













 













макс

sign sin(sin )



 .

Для сравнения

, полученного невариационным методом, см.

[564]. С.73.

399

Максимум момента в этом случае имеет место при



;

 

012

; 2

012

  ; ...

 

012

и равен 

макс

При 

12 12

2

С J

экв

решение уравнения (12.73) будем ис-

кать в виде

 





  

M t M t A Bt e

12 2

   



макс

sign sin( 



) , (12.78)

где

— постоянные, которые в соответствии с упомя-

нутыми выше начальными условиями будут соответст-

венно:

A M t

   

макс

sign sin( ) ;





B M t

  

макс

sign sin(  ) 1 ;





 

экв

;   

012



С J

экв

Общее решение (12.78) перепишется в виде:

 





  

M t M t

  

макс

sign sin 

 













 













































 

1 1

12 12

t e

 



экв экв

экв

. (12.79)

Анализ (12.79) показывает, что в этом случае момент







M t

при



равен нулю, а своего максимума достигает

при









lim  

M t M



макс

, т. е. процесс в упругом

валопроводе имеет монотонный характер и динамический

коэффициент этого звена электропривода достигает своего

критического значения, равного единице.

К аналогичному выводу можно прийти, рассматривая опас-

ное динамическое воздействие в валопроводе электропривода

(электромеханической связью в электродвигателе пренебрегаем)

при 

12 12

2

C I

экв

400

Рассматривая кривые, построенные по (12.79) для кон-

кретного электропривода с различными эквивалентными

моментами инерции и с различной степенью жесткости со-

единительной муфты валопровода (рис. 12.19, 12.20, 12.21),

можно заключить, что при малом затухании в упругом эле-

менте (

0 ) коэффициент динамичности достигает сво-

его максимума

 2

а затем по мере увеличения 

за

счет снижения жесткости упругого элемента полумуфты

(

) монотонно убывает, достигая единицы при критиче-

ском коэффициенте демпфирования, соответствующем



12 12

к эквр



C J

При 

12 12

к эквр



C J

даже при отсутствии ограждения

темпа нарастания момента сопротивления (т. е. темпа пуска

электропривода при

 





M t f n

c e

  , или кратковременных

перерывах в системе питания электродвигателем, динамиче-

ский коэффициент не превосходит единицы и, следователь-

но, колебания отсутствуют.

Запишем дифференциальное уравнение малых вынуж-

денных колебаний упругой системы валопровода (12.62),

считая заделанным приемный конец вала механизма, и в ка-

честве обобщенной периодической внешней силы или воз-

мущающего момента примем переменную составляющую

электромагнитного момента вентильного двигателя по [13]

(см. п.11.3, рис. 12.19), получим:













p p M t M t

012

12 01

2       , (12.80)

где переменная составляющая электромагнитного момента

вентильного двигателя [354]:

 

 

M t M t





























tg -

2 6 2

sin sin

  

 ;