Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 2
Подождите немного. Документ загружается.

281
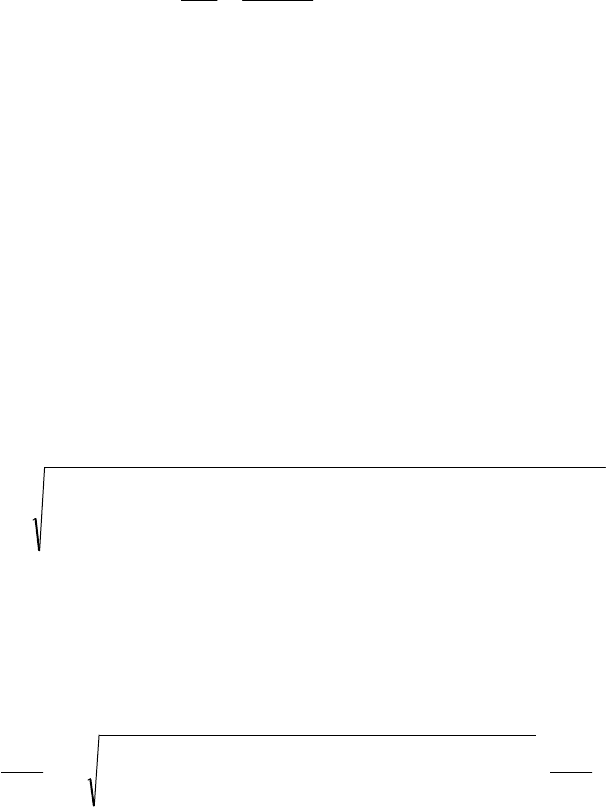
b L L I L L
F i
b L L I L L
F i I L F i
b L
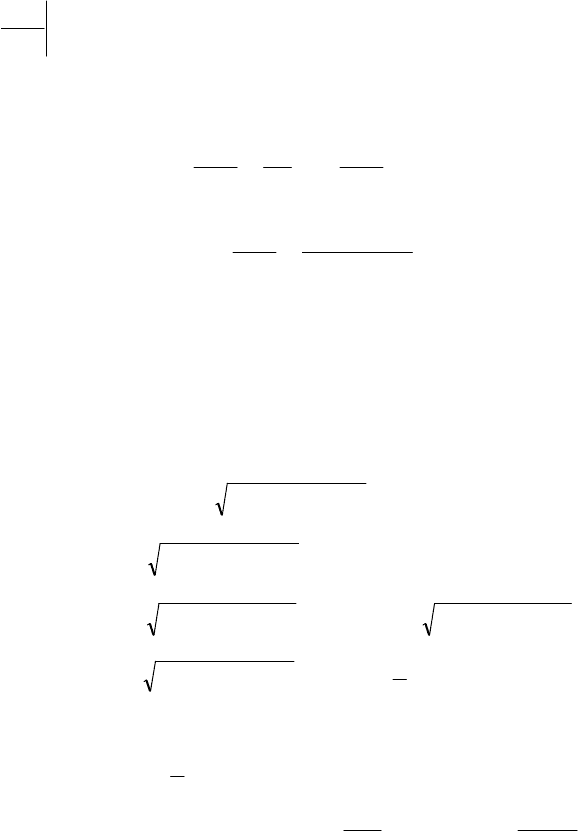
d q
ad d
f
d q
ad d
f
ad
f
4 6
4 2 2
1
2 2
1
3
1
2
1
4 7
4 2 2
1
2 2
1
2 3
1
2 2 2
1
1
4 8
2 2
9
2
9
4
2
2
9
2
.
.
.
( ) sin cos ( )
( ) sin cos ;
( ) sin cos ( )
( ) sin ( ) ( ) sin ;
( )
п
п
п
ad
f a d d
d q ad f
d q ad f
F i L L I
b L L r I L F i r
b L L rI L F i r I
b L
3
1
2
1
4 9
4
1
3
1
2
1
410
4 2
1
3
1
1
1
4 11
3
9
4
2
9
4
2 2
2
9
2
( ) sin cos ;
( ) ( ) sin ( ) ( ) cos
cos ;
( )( ) sin ( ) ( ) cos
sin ;
( )
.
.
п
п
п п
ad
rI
b r r R I r R
U U
b rI
r R I U U I
R
п
экв п экв
п в
п
экв п п в п
экв
cos cos ;
( ) cos ( ) ( )
( );
( ) sin
( ) ( ) .
.
.
1
2
1
4 12
4 2 2
1
2
4 13
4 2
1
1
2
9
4
2 2
2
9
4
2
2 2 2
Для получения окончательного выражения коэффициента
чувствительности по (11.197) в явном виде необходимо реа-
лизовать подстановку (11.198) неизвестных частных произ-
водных: входного тока инвертора
I
п
, угла опережения отпи-
рания вентилей инвертора
1
, нелинейной аппроксимирую-
282
щей функции
F i
f
( ) и эквивалентного сопротивления
R
э к в
по управлению.
Определив частную производную входного тока инверто-
ра по управлению из решения (11.182) с учетом равенств
a a
i i
4 2
(где
i
0 1 2; ; ), получим:
I
i
a
a
i
a
a
i
a
a
i
f f f f
п
4 3
4 0
4 4
4 1
4 5
4 2
.
.
.
.
.
.
, (11.199)
где постоянные коэффициенты при производных правой
части
a a
4 3 4 4. .
; и
a
4 5.
определены уравнениями коэффициен-
тов (11.192), а функциональные коэффициенты
a a a
4 0 4 1 4 2. . .
; ;
уравнениями коэффициентов (11.182) соответственно. Вос-
пользуемся выражениями функциональных коэффициентов
уравнения (11.182) и определим их частные производные по
управлению, получим:
a
i
a
i
a
i
a
i
L
F i
i
a
i
a
i
f f
f f
ad
f
f
f f
4 0 2 0
4 1 2 1
1
4 2 22
0
0
. .
. .
.
;
( ) cos
( )
;
.
(11.200)
Следовательно,
I
i
a L
F i
i
a
F i
i
f
ad
f
f
f
f
п
4 4 1
4 6
.
.
( ) cos
( ) ( )
. (11.201)
Частную производную угла
1
и эквивалентного сопро-
тивления
R
э к в
примем по выражениям п.11.7.2:
283
1
4 7 4 8 4 9
a
i
a
R
a
i
f f
. . .
; .
э к в
(11.202)
где коэффициенты при частных производных правой части
(11.202) определяются по соотношениям коэффициентов
(11.194) (см. п.11.7.3):
a a a a a a
4 7 3 9 4 8 3 10 4 9 3 8. . . . . .
; ; .
Частную производную нелинейной аппроксимирующей
функции
F i
f
( ) определяем согласно приведенному алгорит-
му расчета коэффициента чувствительности, пользуясь ана-
литической формой задания этой функции и ее коэффици-
ентов, приведенных в [350].
Выполнив необходимые подстановки в (11.198), най-
денных частных производных по (11.201) и (11.202), получим:
b
i
b
i
a b b
F i
i
b
i
b
b
i
b
i
a b b
F i
i
b
i
b
b
i
b
i
a b
f f
f
f f
f f
f
f f
f f
4 0
4 7
4 6 4 6
4 8 4 7 4 14
4 1
4 10
4 6
4 9 4 11 4 10 4 15
4 2
4 13
4 6
4
.
.
. .
. . .
.
.
.
. . . .
.
.
.
( )
( )
;
( )
( )
;
. .
.
( )
.
12 4 13
4 16
F i
i
b
i
b
f
f f
(11.203)
Определим коэффициент чувствительности (11.197) после
подстановки (11.203) и приведения подобных членов. Полу-
чим:
i
b b b b b b
i
b b b b b b b
i
b
f f
f
( )
( ) ,
. . . . . .
. . . . .
.
. .
4 3 4 7 4 4 4 10 4 5 4 13
4 3 4 14 4 4 4 15 4 5
4 16
4 17 4 18
(11.204)
284
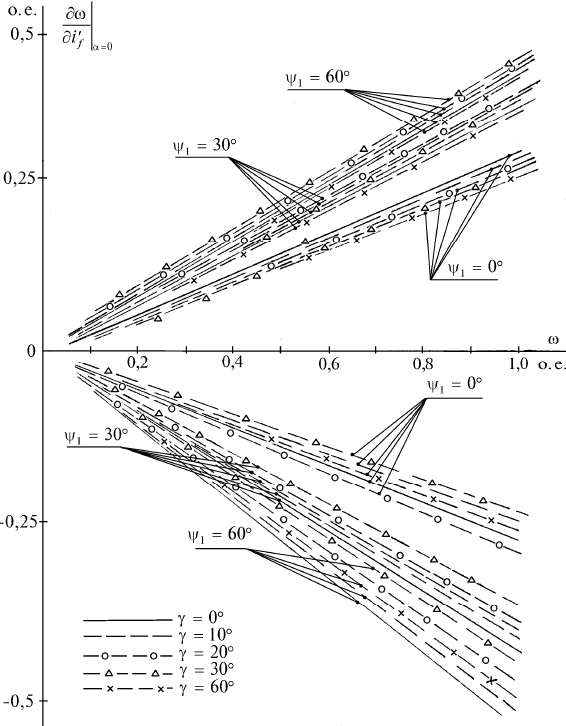
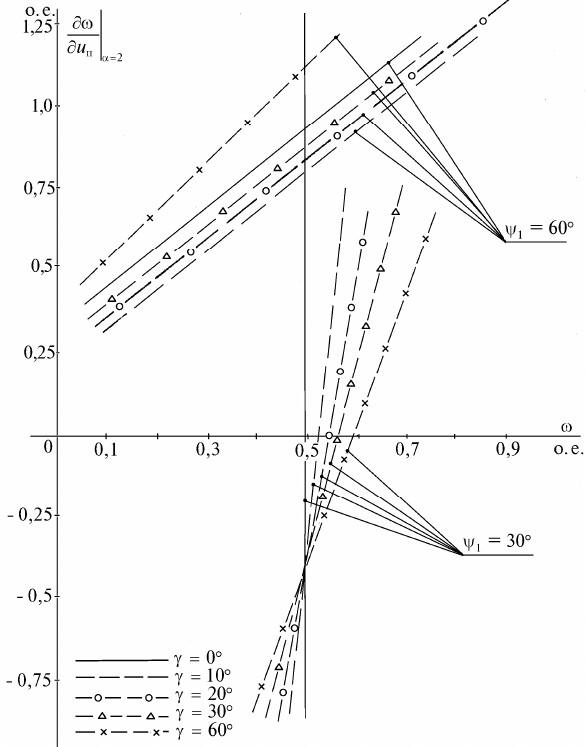
Рис. 11.25. Рассчетные коэффициенты чуствительности регулирова-
ния скорости ВД по управлению током
i
f
при постоянном момен-
те статического сопротивления
285
откуда
i
b
b
b
f
4 18
4 17
4 19
1
.
.
.
( ),
где
b b b b b b b
b b b b b b b
4 17 4 3 4 7 4 4 4 10 4 5 4 13
4 18 4 3 4 14 4 4 4 15 4 5
4 16
. . . . . . .
. . . . . .
.
;
.
Расчетный коэффициент чувствительности
b
4 19.
( ) по
(11.204) определяется алгоритмом расчета, рассмотренным
выше. Расчетные характеристики приведены на рис. 11.25.
11.7.5. Чувствительность регулируемой координаты
по
управлению по U
п
при моменте статического сопротивления
с
2
Решив уравнение (11.178) при
2
относительно регу-
лируемой координаты, получим:
L F i I L L I M
M M
ad f d q co
c co
( ) ( ) cos ( ) ( ) sin
.
п п1
2 2
1
1
2
(11.205)
Уравнение (11.179) и все соотношения коэффициентов
остаются неизменными.
Определив частную производную регулируемой коорди-
наты
по управлению
U
п
по изложенной в п.11.7.2. мето-
дике, получим:
U
L F i I
L L I M
M M
U
ad f
d q co
c co
п
п
п
п
2
2
1
2 2
1
1
( ) ( ) cos
( ) ( ) sin
.
(11.206)
286
Осуществив подстановку в (11.205) значений
U
п
1
по (11.206) и (11.185) и заменив квадратный ко-
рень в (11.206) значением
, как это следует из (11.205), по-
лучим:
U
b
U
b
п п
1
2
5 2 5 3. .
откуда
U
b
b
п
5 3
5 4
2
.
.
( )
. (11.207)
Коэффициенты
b
5 2.
и
b
5 3.
определяются соотношениями:
b a a a a a a b
b a a a a b
5 2 5 1 5 4 5 2 5 5 5 3
5 6
5 1
5 3 5 4 5 7 5 2 5 8 5 1
. . . . . .
.
.
. . . . . .
;
;
где
a a a a a a a a
5 1 2 0 1 1 2 1
2
2 0 2 2 2 0 2 2
4 2
. . . . . . . .
2 4
2 0
2
2 1
2
2 0 2 2
1
a a a a
. . . .
;
a a a a a a a a a
5 2 2 1
2
2 0 2 2 2 2 2 0
2
2 1
2
2 0 2 2
1
4 2 4
. . . . . . . . .
;
a a a a
5 3 2 1
2
2 0 2 2
1
4
. . . .
;
a
5 4
4
9
4
.
( )
r L L r L L
d q
d q
2 2 2 2
1
2 2
1 1
2 2 ( sin cos ) ( ) sin
cos ( ) ( sin cos )
2
1
4 2 2 2 2
1
2 2
1
9
4
r L L
d
q
r L L r R
R
d q
( ) sin sin ( ) ;2 2
1
2
1
1
э к в
экв
287
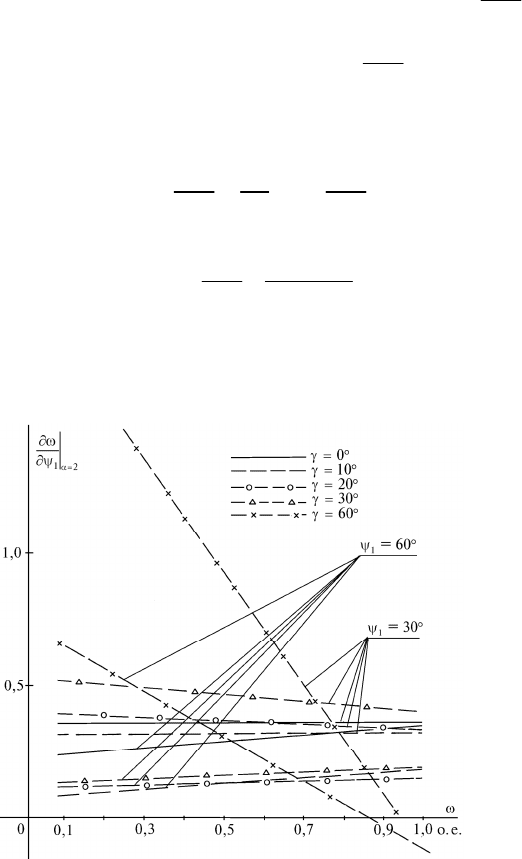
Рис. 11.26. Расчетные коэффициенты чуствительности регулирова-
ния скорости ВД по управлению направлением U
п
при вентиля-
торном характере момента статического сопротивления

288
a L F i L
L F i r L
r R
R
a r R a L F i
L F i
ad f d
d f d
ad
f
ad
f
5 5
3 2
1
2
1
3
1 1
2
1
1
5 6
5 7
2 2 2 2 2
1
2 2 2 2 2
1
9
2
9
2
2
2
9
2
9
2
.
.
.
( ) ( ) sin cos
( ) ( ) cos sin
sin ( ) ;
( ) ; ( ) ( ) cos
( ) ( ) sin
экв
экв
экв
1
5 8
2
; .
.
a U U
п в
b L F i L L I
ad f d q
5 1 1
2
1
2
.
( ) ( ) cos ( ) ( ) sin
п
M M
c co
1
.
Расчет коэффициента чувствительности по (11.207) про-
водится по алгоритму, изложенному выше. Расчетные харак-
теристики приведены на рис. 11.26.
11.7.6. Чувствительность регулируемой координаты
по управлению
1
при моменте статического сопротивления
с
2
Определим частную производную координаты
по
управлению из (11.205):
1
1
2 2
1
1
1
2
2
L F i I L L I M
M M
ad f d q co
c co
( ) ( ) cos ( ) ( ) sin
,
п п
(11.208)
где
1
1
1
1 1
L F i
I
I
ad f
( ) ( ) cos sin
п
п
289
( ) ( ) cos sin
.
. .
L L I I
I
b
I
b
d q
c co
2 2
1 1
1
1
6 1
1
6 2
2 2
п п
п
п
После соответствующих подстановок в (11.208) с учетом
(11.205) получим:
1
6 3
1
6 4
1
2
b b
. .
,
откуда
1
6 4
6 3
6 5
2
b
b
b
.
.
.
( ) . (11.209)
Расчет коэффициента чувствительности по (11.209) про-
водится по алгоритму, изложенному выше. Расчетные харак-
теристики
b
6 5.
( ) приведены на рис. 11.27.
Рис. 11.27. Рас-
четные коэф-
фициенты чуст-
вительности ре-
гулирования
скорости ВД по
уп-равлению
углом
1
при
вентиля-торном
харак-тере мо-
мента статиче-
ского сопро-
тивления
290
11.7.7. Чувствительность регулируемой координаты
по
управлению
i
f
при моменте статического сопротивления
с
2
Частная производная координаты
по управлению
i
f
при
2
может быть получена по аналогии с п.п. 11.7.5. и
11.7.6. из (11.205):
i
L F i I
L L I M
M M
L F i L L I
I
i
L I
F i
i
M M
f
a d f
d q co
c co
ad f d q
f
a d
f
f
c co
2
2
2
1
2 2
1
1
1
2
1
1
1
( ) ( ) cos
( ) ( ) sin
( ) ( ) cos ( ) ( ) sin
( ) cos
( )
.
п
п
п
п
п
Выполнив все операции по определению функциональных
коэффициентов и их производных по аналогии с п.11.7.4. и реа-
лизовав соответствующие подстановки, получим:
i
b
i
b
f f
1
2
7 3 7 4. .
откуда
i
b
b
b
f
7 4
7 3
7 5
2
.
.
.
( ), (11.211)
где
b b
7 3 6 3. .
;
b b
7 4 6 4. .
. определяются соотношениями, по-
лученными в п.п. 11.7.6.
Расчет коэффициента чувствительности по (11.211) про-
водится по алгоритмам, изложенным в п.11.7.4. и 11.7.5.
