Antontsev S.N., Kazhikhov A.V., Monakhov V.N. Boundary Value Problems in Mechanics of Nonhomogeneous Fluids
Подождите немного. Документ загружается.


238
Chaoter
5
where
E
i
0
is
an arbitrary number. The
last
relations together
with
(5.30)
results finally to Gronwall inequality
(
b2 ch.
1)
from which according to (2.18)
s2
ch.
1
it
follows that
s
f
i).
4.
Singular problem
(0
5s
5
I).
In this case
as
it
has been shown in 33 reduced saturation
is
a
mesurable function in
Q
and satisfying the identity (2.2)
and
in-
equal
it
ie e
LE
s(x,t>
5
1,
(la
)v
s
12111,
%<
I,.
.
(5.33)
Nevertheless
for
the known summed filtration velocity being
limi-
ted, this distribution
of
saturation
is
found to be unique.
Theorem 5.7 (uniqueness
of
solution). Let the conditions (i)
-
(iv)
3
2
be satisfied
(of
the existence
of
a
generalized solution) and
suplementary
3
then the generalized solution (in the sense
of
the definition
(2.1))
of
the problem (5.2)
-
(5.4)
(0
5s
51
)
is
unique when
The proof
is
made from the oppositie.
Let
two solutions
s(x,t)
,
eeist. Composing the difference of the
r=
r‘
(or
when
P=r’
and
B=O
).
i
=1,2,
s
=
s
1
-
s2
respective identities (2.2) we obtain that
s
satisfies inequa-
lity
(5.35)

Filtration
of
Immiscible Liquids
239
Here
Now let
K
(x)
be a consequence of smooth functions converging
almost
everywhere in
Q
to
Ko(x)
and satisfying (i)
9
2,
and let
an admitted function Cp(X,t> be sufficiently smooth. (5.35) takes
the form
06
Uere when
r
=I7'
the
last
term in
(5.36)
is
absent because
s(x,b)
on
S
is
almost everywhere equal to zero, and
v
Cpis
bounded.Consi-
der the sequence of boundary problem solutions
3
'Pt+
A,
"KO6 DO)+
G
v(p
=
p
,
(x,
t)
E
<
,
(5.37)
1
cp
(x,T)=O,
x
E
a;
(pis=
0
(Kob
v'pn
-0
in
the case
I'
=1
),
(5.38)
1
s-
where
Ae(x,t)
is
a
sequence
of
smooth functions converging
to
A(x,t)
almost everywhere in
Q
and such that
A,
I
h
+&
,
and
S
p=J
a(x,
<)%
.
From the results
of 1,2
it
follows
that
the
so-
lution
of
the problem (5.37), (5.38) for
E
>
0
always exists and
at least
cp(x,t)
E
vJ2
"(k).
Obtain for
cp
evaluations independent
of
E,
6
*
To
do
this
we multiply (5.37)
by
V(IiobV
(p)
and
usual
transformations yield inequality
s1
4
for which
dition of the theorem
1'
=
1"
is
used in the case
P
Ir
=
0.
But under the con-

240
Chapter
5
Therefore (5.39) results
in
inequality
or
after applying inequality (2.18)
Y
2
ch.
1
for
y
E
11
v
qII:,Q
2
(5.41)
II
vcp(
2)
II
+
llhl'z
V(ICO6
vcp)
5
C(Il>
.
Now introduce
cp
(XI*>
in inequality (5.36). Then
it
takes the
form
=
J-
((
hE-
A)
V(I{
vq),ms
(P,
us)
=
J+
J,
%
'LI:
and obviously
from which
it
follows that
inequality (5.35) can be established for a derivative by time.
Theorem
5.0.
Let the conditions (i)
-
(iv)
92
be satisfied,
I?
E
A'
s=
sl-,s,
-0
almost everywhere
in
VL*
In
case when
I
=
1'
(or
I'
=
r
)
the analogue
of
the second
and in addition
--t
-3
--t
(
IIps
i
bs
v
llm,4
IIavsol12,q
;
IIdiv
p
l12,u
15
'$1
9
(5.42)
here
sotlr
=
0.
Then there exists a gene-
ralized (by definition
s2
)
solution
s(x,t)
of
the problem
(5.2)
-
(5.4),
on which the bounded function
z(x,t)=
sad5
E
1,'=
I'
or
P2=
1'
and
0
and in addition
to
(5.33)
zt
E
L2(%)*
We begin the proof from the estimates for regular problem, when
-
a,(s)=
a(x,s)/
Fc(x)
+
E,
E
>
0.
The function
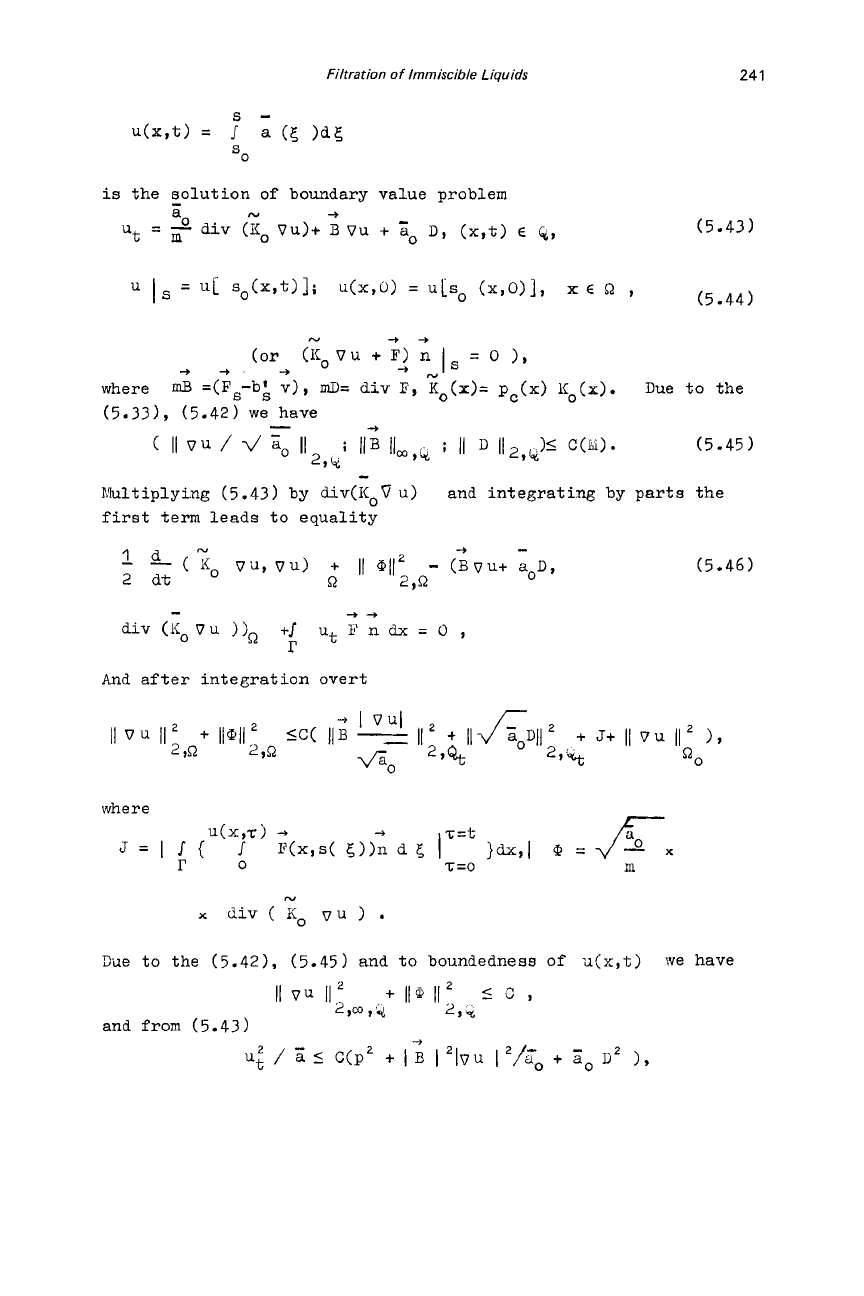
Filtration of Immiscible Liquids
241
is
the Bolution
of
boundary value problem
N
+
(5.43)
0
a
ut
=
;a
div
(KO
vu)+
B
vu
+
go
D,
(x,t>
E
6,
(5.44)
u
Is
=
u[
so(x,tll;
u(x,ii>
=
UCS,
(x,O)],
x
E
Q
,
(or
(KO
Vu
+
F)
n
ls=0
>,
++
-3
+-
where
(5.33), (5.42) we have
mE!
=(Fs-bk
v),
mD=
div
F,
'Ko(x)=
p,(x)
K0(x).
Due to the
-
-
Multiplying (5.43) by
div(KoV
u)
first
term leads
to
equality
and integrating
by
parts the
++
-
div
Vu
I),
+I
ut
b'
n
dx
=
o
,
r
hd
after integration overt
where
u(x,z
J=lJ{
I
r
0
div
Sue to the (5.42), (5.45)
End
to boundedness of
u(x,t)
we have
II
vu
112
+
112
5
c
,
ZY"9.1
2,U
and from (5.43)
-3
ut
/
a
5
C(y2
+
1
B
I
'1vu
I
'/k0
+
go
D2
),

242
Conse quent ly
r-
Chapter
5
(5.47)
Thus, the sequence
of
the functions
z(x,t)=
Is
God
g(
v
z
=
=+ao
v
s=
v
u~~'/')
is
uniformly bounded
in
l!i:(~)(ll
zll
rv;(y)
5
C>.
To complete the proof one
is
to transit fully to the
limit
for
Remark.
In
a
one-dimensional case
(n
=I
)
the
first
of the
in-
equalities (5.47) provides
u(x,t)
over
a
variable
x,
since
0
E
-+Osimilarly
as
in
b3.
lu(xpt)
-
u(x,
,t>
I
5
I
x,
-xp
I
'I2
11
vu
(1
2,
m,%
It
will
be shown in
68,
that this
is
enough according to the
known results 192 ]to solve singular equations
of
the kind (5.43)
for
~(~,t)
and over
a
variable
t,
So,
in
the considered case
u(x,t>
EC@'
(T)
and
s(x,t)
E
c(:)
respectively. In addition
if
6.
ON
A
JOINT
PROBLl3M
1.
Problem design
It
is
shown here how and
to
what extent the results ofb 4,
5
can
be used
for
the study of smoothness
of
joint problem solution
(stationary and non-stationary) of two-phase liquid filtration in
inhomogenious anisotropic ground. The detailed discuosion
of
this
problem
is
presented
in
9,
8.
now we are going to consider the
further smoothness of the generalized solution
s(x,t),
p(x, t)
of
a
boundary problem obtained in
b
3.
+-+
mst
=
div(
iio
a
vs-
b
v
+
p),
(x,t)
E
Q,
(6.1
1
-+
-$
-+
div
(K
Vy+
f
)=
0;
1
v
=
LVp
+
f,
(x,L)
E
sG
,
which coefficients are defined by formulas (1.19) and satisfy the
conditions (i)
-
(iv)y 2 (of existence of
a
generalized solution).
2. Regular problem
which the qonditions (2.6) are-+satfsfied
(x,t)
E
a;
F
n
=
0,
(x,t)
E
S1
(0
<
So
I
s(x,t)
5
1
-
6,
<
1). Let's begin with the problems in
(6.5)
div
F
=
0
,
and
a
given function
so(x,
t)
satisfies inequalities

Filtration
of
Immiscible
Liauids
243
0
<
bo
5
s0(x,
t)
5
1
-
6,
<
1.
(6.6)
Then in agreement with the maximum principle from
2
almost every-
where in
4:
0
<
6,
5
S(X,
t)
5
1
-
6,
<
1
(6.7)
and consequently, there don't exist regions
with
residual values
of
eaturation
in
the flow, equation (6.1)
is
parabolic
in
Q
,
and
problems
(6.1)
-
(6.4)
is
called regular.
Theorem 6.1. Let conditions (i)
-
(iv)B
2
be satisfied (of exis-
tence of a generalized solution) and
IIKolIc(~)
5
Ido.
Then for
any generalized solution
(s,
p)
problems (6.1)
-
(6.4) in two-di-
mensional case
n
=
2
the following inequality
is
valid:
where
C
only depends on constants in conditions (i)
-
(iv),
Additionally
if
I?
E
If:
and
hio,
bi
>
0
in
(6.7) and on a distance from
k*
to
&.
q>n+2,r>n,
(6.9)
then
for
any
generalized solution
at
n
= 2
11s;
PI1
c"(,>
5
c,
>
0.
(6.10)
In
a
three-dimensional case (n
=
3)
estimations (6.81, (6.10) are
true
if
the function
k(s)
=
kol
+
k,,
satisfies the inequality
(6.11)
where
A,
is
a
constant
in
lemma
4.1.
The proof
is
commenced by obtaining
a
more complicated estimate
(6.10).
In
agreement with the theorems (4.11, (4.2)
in
a
iven
case
for
a
generalized solution p(x, t) problems (4.11, 74.2)
with the inserted saturation
s(x,
t)
there exist evaluations
-+
-3
IlVIlpq
,q
=
IIKVP
+
fllr,m,q
5
C,
r
>
n.
Then
with
the problem-+(5.2)
-
(5.4)
in
view (with
a
given summed
filtration velocity
v(x,
t))
by theorem 5.4
we
obtain s(x,
t)
E
-3
E
C"(,)
and IIs(x, t)IIcuC:)
5
C.
Consequently
{k[x,
s(x,
t)],
f[x, s(x, t)]}
EC($
and already the theorem 5.5 results in

244
Chapter
5
5
c.
Internal estimate
(6.8)
is
proved in an absolutely
similar
way.
Theorem 6.2. Let conditions
(i)
-
(iv)
9:
2
and given functions of
variables
x
E
9,
s
t
[0,
I]
satisfy the conditions
then for any generalized solution
(s,
p)
,
s
E
C
a
(Q~)
of
the
problem
(6.1)
-
(6.4)
estimates are valid
-
(6.12)
where
C
is
dependent on
a,
y,
hi
of variables in conditions (i)
-
(iv)
bi
>
0
(6.7) and on a distance from
k1
to
h.
For
1
=
2
s(x,
t)
E
c2+a
,I+
(%O,
P(X,
t)
EC
a+a91+a(~*)
i.e. the solution
would
be
classical..
In addition
if
((ID,s;
1
$1
I
i
IIDlxf's;
DF'P~~~,~,)
5
C,
q1
c
q,
c
(t
1
r
E
dtl-2
and the respective agreement conditions are satisfied (see 51,
then (6.12) occurs
in
Q
generalized solution
(s,
p),
s(x,
t)
E
C
"(,).
d
=
((x,t)
E
%:
uiinlx-yl
L
b
>
0)
for any
Y
EslnsZ
++
Proof.
As
it
follows from the theorem
(ICoa,
K,
F,
f,
b)E
C"(kl).
Then by the theorem 6.1
D
p
(v(x,
t))
respectively)
belongs
to
Lq,m(d')
theorem
5.2
that
0s
E
L
(%I)
means due to (5.21) and
D$
E
L
theorems 5.2
-
5.5 provides
(vs,
ted for
1
=
2.
Similarly evaluation
is
establishing in
C;
.
Remark.
It
follows from theorems 6.1
-
6.2 that the
initial
point
for increaRing the
further smoothness of
a
generalized solution
(s,.p)
of
a
regular problem (6.1)
-
(6.4)
"in
whole" over
t
E
10,
'I']
and
1
5
nS
3
is
s(x,
t)
in
Q.
In
a
three-dimen-
sional case the proof
of
continuity
s(x,
t)
for
all
1;
E
LO,
T]
imposes the condition (6.11)
on
the coefficient
k(s)
=
k,,
+
lc,,
of the equation (6.3).
If
this condition
is
not satisfied
s(x,
t)
can be
only
proved for
t
E
LO,
To]
is
defined
by
a
given problem.
assuming the theorem for
S(X,
t)+
we obtain from the
i.e.
(Dg;
DZ)
E
L
Y,
O0
9
which
9
(y1),Dxv
E
I,
?,I).
This
due to
p)
and everything can be repea-
6
where
0
<
To
<
T

Filtration
of
immiscible Liquids
245
Theorem
6.3.
Let the conditions (i)
-
(iv)§
2
and (6.9) be
satis-
fied, where
I?
E
Hz .
Then there exists
To
>
0
stants from conditions (i)
-
(iv)s
2,
Id,
6i
>
0
such that for any generalized solution
(s,
p)
of the problem
(6.1)
-
(6.4)
defined by con-
from (6.7)
is
5
c.
Proof. Let present
a
s)
in the form
N
k(x,
S)
=
k(x)k-'(so),sO=
so(x,
O),
N
and notice,
that
k(x,
so)
=
1,
Vx
E
Q.
Consider an auxiliary problem
in
which k(x,
s)
kE(x,
s)
=
1
+
Ask[x,
so
+
xE(Ass)],
has
been changed by
N
where
xE(<>
=
5,
E;
E
[O,
€1
and
xE(<)
=
E,
<
>
E
for which
x(g)
=
-x(-B,
5
5
0
andAsf
=
f(s)
-
f(so)
Vf(s)
E
C[0,
IJ.
N
Assuming that
kE(x,
s)
together with
k(s)
is
continuous over
s,
choose fixed
E
2
0
from thewcondition
11
-
kEIA,
=
lAs
kElA3
<
1.
N
Here due to continuity of
A
over
q
for
kE
the ineguality
(4.15) with
9,
>
5
holds and consequently
vp
and
v
belong to
L
(-1.
Then considering the equation (6.1 for saturation, on
the basis of the theorem
5.4
we obtain
that
s(x,
t)
E
C
"(G),
a
>
0
and particularly
4
b'
(6.13)
0
IA,s~
=
Is(x,
t)
-
s
(x)l
<-
C(E,
i,,)t",
a
>
0.
Supposing
To
=
(E/C)
we find
that
lAsSl
5
E
Vt
xE(Ass)
=
Ass.
Consequently
E
[O,
Toit
and
so
N
N
kE(X,
s)
=
k(x,
s),
t
E
10,
To],
and
a
solution of an auxiliary problem
is
at the same time
a
solu-
tion of an initial one. The theorem has been proved.
Theorem 6.4.
In
a regular problem the further smoothness
of
a ge-
neralized solution
(s,
2)
obtained in
$33
for
all
t
E
Lo,
T]
is
defined forn
=
2
ints
(x,
t)
E
S'
nS2)for
all
t
[O,T]In
a
three-dimensional case
when the condition p6.11
is
satisfied and undoubtedly for
0
<
t
<
To
only by smoothness
of problem data (exept po-
(n
=
3)
a shilar roperty of generalized solution
is
kept only
whereT,
>
0
is
defined by the problem data.

246
Chapter
5
3.
Degenerat i.ng problem
In
the presence
of
regions with the residual saturation value8
in
a
flow
as
it
has been proved in
B
3,
for the generalized solution
of the problem (6.1)
-
(6.4) the next estimates are valid
Now
we show that this solution
is
integrally continuous in Hb'lder
sease.
Theorem
6.5.
Let in addition to conditions (i)
-
(iv) !$2 inequali-
ties hold
(I
-
s)"sP
<-
ilia,
2
<
s,
<
q,
v
>
0,
I
<
A
<
a.
Then
(6.15)
(6.16)
where
s
z
,il
=
s(x+h,
t+
z)-s(x,t),
I*
=I
+
a
+
p
)
H
<
nq,
/(n-yo),
n
2%;
M
=
m
9
'io
>n,
Po
=I*
(
A,'b
,
"1
>
0.
0
Proof. The inequality (6.15)
is
a consequence
of
the compactness
principle from
32.
To
rove (6.16)
it
is
enough to refer to in-
equalities (4.251, (4.29) take into account that in
a
given case
+
(I
KT
I)
IfT
1)
<cI
sz
I
.
7.
STATIONARY
PROBLEMS
1.
Existence of generalized solutions
Formally assuming
in
equalities
lil
=
0)
a-
(S~,~-',,R)
=
0,
x
E
a
(
aB
5
r1
n
r'),
at
we come
to
the following stationary boundary problem for
(s(x),
p(x))
:
++
3
3-3
div
(ioa
vs-
bv
+
F)=
-
div vl=
0;
s
(7.1)
Theorem 7.1. Let the assumptions (i)
-
(iv) be satisvied8
2
on
coefficients
of
equations and boundary values
of
the problem
(7.11, (7.2). Then there exists a generalized solution
~(x),
p(x>

Filtration
of
Immiscible Liauids
247
of this problem
(in
terms of the definition 2.1 for
U=
0,
a%
(so,
R)
0
,
for
which under
n
I
2
the estimates are
valid
VSY
v
P
IlZ&
i
(I
P
II
(
lla1'2
)
6
C(bJ,
0
6s
'I
.
(7.3)
M,Q
If
in addition the conditions (2.7) are satisfied, then
0
<
6,
5
s(X)
5
1
-
6,
<
I
.
The roof
is
similar to $3. Searching for the problem solution
(7.17, (7.2)+i.n the
form
of decompositions
(3.1)
with
unknown co-
efficient8
a''
=
(a;
,...,
a;i
>,
bLY
=(byl..
.,bfi
),
we come to the
following analogue
of
the equation system (3.21, (3.3):
y
II
+,,
(7.4)
+:~T
+
+,-
-+
k
a"
+
p
=
i)
,
B
b"
+
y
=
i)
,
where squared matrices
(ITx
1:)
ii
={a,
},
B
=
{p.
}
and vectors
B
=
(P
9
- -
,pi{>
9
y=(
y,
a
-
2
ylJ
1
Jk,re continuous functions of
simply solvable in respect to
b'"
dependent
on
zl'
=
ZN(2''
)
and
3''
dent
of
2". Substituting
%I'
=
%"(%"
)
in coefficients
of
the
first
equation (7.4) we get that
A=
A&'
)
are continuous over
$'
here
+
3
+
Z'',
3'
-In
agreement
with
1s
3
the
second equation (7.4)
is
its
solution
is
continuously
bounded by a constant Fndepen-
and
p
and
3
=$(@
)
-t
+ii
--t
--tlJ
+--t
(A
a
+
p
,
a
I
~~(11,
c)(J'
,
a")
-
c
11
s,li~~
11
'
. (7.5)
$;(
Q
1
Inequality (7.5) provides the solvability of the
system (7.4) for
all finite the evaluation (3.8) independent of
N,E,
h
has already been obtained. Prom
the
analogous identity (3.4) cor-
respondi.ng to a stationary problem
it
follows
that
(7.6)
Inequalities (,3.6), (3.8) and (7.6) enable
us
to isolate subsequ-
ences from
{
S''
,p14
}
converging almost everywhere to
Q
and on
r
which derivatives weakly converge in
L
(
a)
limit
for
14
--f
m
Due to the maximum psinciple for
s(x)
(3,
52)
and the theorem
4.1
we obtain
that
the limited functions
(s,p)
are bounded.
N.
For
PI'
I(
VSI!
(1
5
C(h,
E
1
11
SG
,Po
11
3
c
(il,
E,
!,I
).
2
,a
+i;
(a
1
and to
transit
to
the
4
Now
using estimate (3.8)(1[
v
l12,QS
C
which means
[Ivhl12
5
C)
from
the inequality
,Q
+
--t
-
(Lo
tl
VS
+
F,
0s)
=
(C
vll
V
s,
5
C(
E,
I,.
)
.
find
I1
0s
II
2,Q
The latter makes
it
possible
to
transit
get the identity
S) (7.7)
(7.a)
to the
limit
over
h
and
