Antontsev S.N., Kazhikhov A.V., Monakhov V.N. Boundary Value Problems in Mechanics of Nonhomogeneous Fluids
Подождите немного. Документ загружается.


208
Chapter
5
The theorem requires both addends in the right side to be equal to
zero, then,
in
analogy with the previous, we get
proved.
Let
s(x)
be
a
boundary solution
of
the corresponding auxiliary
stationary problem, for whichvraimaxsdd<mWe show that actually,
-
s
1
0
(s
=max{bO-
-
s,
0
}
P
0
).
The theorem for the non-stationary case has been
61
=
max
s
=
M
5
1.
1
r'l
Admit
the opposite: Let
vrai
nax
s=
hi>
id,
.
tion
s
'=
0
on r2AVith
s
Vbeing substituted in
(2.5*),
and
F4
taken
into account, we are led to the equation analogous to
(2.8)
Consider the func-
a
s
"(x)
=II~~X
{
s(x)-u
,0
}
where
Ll
>
v
L
MI
and obviously,
-b
-
+
(lc0
a
v
s,
v
s
'
+
(c
VhV
s,
s
"
ov=
{X€
a
,
s(x)
>
u
}
.
Hence, bearing
in
mind inequality
(2.23)
ch. 1
it
appears
and since
ales
Qv+
0
for
u
-t
id,
there exists
v
<
111
such that
U
su
E
0
it
means (due to the condition
svI
sz
=
3)s
=
0
,
i.e.
s
5
u
<
valid. Inequalities
s
20
and (2.6*) under conditions (2.7)
Remark
1.
Taking into consideration
formulas
(1.21, (1.19) we have
Iii.
So,
the assumption
vrai
xnds
=
i~
>
ivil
is
not
Regularity conditions
(2.7)
correspondingly take the form
imposing
limits
only on the known beterogeneity and anisotropy
of
the medium and on the location
of
I".Conditions
(2.7*)
in the

Filtration
of
Immiscible Liquids
209
assumption
lowing
physical interpretation. Equalities
(2.7
)hold,
if
1)
plan filtration
is
considered, gravity being not taken into
2)
liquids are of the
similar
density;
3)
a
medium
is
isotropic
an
homogeneous in the direction
of
a
ng
IF,
=
0.
Remark
2.
From the theorem
it
follows that identities (2.5),(2.5*)
actually hold with coefficients
=
a+
E
and
C
=
bs
but not
those extended over
s
.
Remark
3.
If
an initial and boundary saturation distribution
sa-
tisfies the conditions
v
Ec=
0
frequently used
in
filtration admit the fol-
account
;
+-3
-3
vector
(s
for which
0
<
6,
5
so
(x, t)
5
1-
6,
<
1
,
then, when assumptions (2.7*) are realized according to inequali-
ties (2.6*) there are no stagnant zones in the flow, where
limit
values
s=i),'l
are reached. Problem
I
in
this case
is
called a
regular problem (in equation (1.7)
a
2
6
>
0
)
are regular.
Generally only inequalities (2.6) hold
and
stagnation zones with
residual values
of
saturation may appear
s
=
0,l
Equation (1.7)
degenerates
(a
2d)
and, accordingly, problem
I
is
called sin-
gular.
4.
Compactness principle for a non-stationary problem solution
The solution of
a
singular problem
I
is
found as a
limit
of a
solution sequence
s
'(x,t) of regular problems a(x,s)
I
E
>
0
for
+
c).
For this upurpose we show that one can isolate
a
con-
vergence subsequence from the sequence
(5'
(x,t)
}
.
Theorem
2.2
(compactness principle). Let the sequence
of
functions
sE
(X,T;J
dimensional
in
Q
satisfy inequalities
and
its
aolutions
and for any
cp
(x,bI
E
vi:(q),
cp(x,t)=
9,
(x,t)
ES',
cp(x,T)
=
0,
-3
x
E
B
integral identity
E
(ms
'-
mso,
cpt
)
r,
=
(B
,
v'p
.
(2.10)
holds. Here
a,(-c)
is
a continuous strictly positive function
(ao(a>
=
ao(l
>=
0,
a
=
a,(z>Ec(x)) for
o
<
T
<
I
and
(2.11
1
Then from the sequence
that due to the
first
of the inequalities (2.9) and in any
L
Is
aO<g
)d
5
sE
(x,t)one can isolate
a
sub-sequence
s
"(x,t>
convergent almost evermere in
Q
and on
s
(it means
1
5q
<
m
Q'
and a sub-sequence on which
Vuv=
0

210
Chap
fer
5
weakly
in
L,(Q)
converges
Fn
v
u
.
If
in addition
Proof. Under the condition of the function homogeneity
M(s)=
a(s>l
compactness results from the known
[96].
In two phase filtration a problem homogeneity condition doesn't
exist (for example
a
=
s
(I-
s
)P
For convenience we consider
a
vector
BE(X,t)
in (2.10) to be given
02
%
=
!J
x(-
m, m
)
BE
=
0,
t
$i![O,
!I!]).
Put
cp(x,t>
=
q(t>
5(x)
in (2.10),bwhere
V(t)
is
an arbitrary smooth finite function, and
rewrite
(2.10)
in the following way:
I
V
s
I
'(M(
As)
#
hhl(s))
0:
--t
inequality
(2.9)
being kept (for example
<(XI
6
iV;(
a)
Hence, from the definition
of
the generalized derivative over
t
it
follows that for almost all
t
E
[O,
!!?I
+
d
dt
-
(
ms
'-
mso
,
51,
=
(B
',
05)
.
IntegratLng the last equality over
t
€[
t,
T+
AT
1
c
[
0,
F]
(-c
>
0,
At
>
0
are fixed numbers),
we
obtain
-
s(x,
-L
)
.
Further, we introduce the function
(2.14)
Since
z(s)
is
a monotone function because
dz
ds
I
-
=
dw
>
0,
s
E
(0,
1)
,

Filtration
of
lmm
iscible
Liquids
21
1
are fixed, then due to (2.141, (2.15)
We replace.
t=
AT.
u
+
T
in the last integral and integrate the
over
t
E
10,
'l'
-
A,].
This leads to
Changing the integration order over
T
and
a
and using Hb'lder
inequality
we
finally find:
But due to (2.91, (2.111, (2.15)
i.e. taking into account (2.11)
II
A,
zE
112,k05
II
A,
zo
Il&b+
On
the other hand,
it
follows
from the
that
E
(1
Ax
z
Ilr,z
1.1
/AX
1,
AxZ
=
Z(X+
A
$Lo
5
c
la,
I
.
(2.16)
second inequality (2.15) tha
(2.17)
x,t)-
z(x,
t).

212
Chapter
5
Moreover, on the base
of
inequality (2.23) oh. 1
II
AT
z'II~,~
5~
II
VA~
from which considering
I1
AT
zE
I1
Ax
ZE
In complete analogy we
(2,151, (2.16) for
q
=2,
cc
=
I/
2
obtain that
Thue, sequence
tions and consequently,
it
is
compact in
L,(y)
means that because
of
finitary (limitation) and in
as well
in
L
(Q)
and
L
(5)
because
it
is
a compact image under
continuous mapping
2
'(x,t)satisfies all the
Riss
criterion condi-
and
L,(S)
S
'(x,t>
is
strongly compact
and
it
L
(4)
and
9
L4(s>>
(1
2
1
But then the sequence
4
s
=8(z).he to the strong compactness from
s
'(x,t>
one can isolate a sub-sequence
(we keep
signation), converging almost everywhere
in
Q,
S.
quence functions
N
SE
2
=
I
.ao(
5)d
5
0
"
converge almost everywhere to
z
=
z[s(x,
t)]
and
is
weakly compact in
Applying the diagonal process, now we isolate the
s
V(x,t) convergent almost everywhere
in
Q
and
S
L,
(L~).
N
I.
its
former de-
On this subse-
N
besides
{v
zE
j
subsequence
to
s(x,t)
and
the sequence on which
v
z
'
in
L,(%)
are weakly convergent to
N
S
v
z
=
V
I
ao(c)g
.The
first
part of the lemma has been proved.
0
To prove
(2.13)
it
is
enough to use (2.161, (2.17) and the inequa-
lity
Remark
4.
Condition (2.12)
is
satisfied
if
IA,
sI
<C
InT
elkresulting
from
(2.12).
ao(s)
L
~~(1-
s>"
s
8,
z0=
const,
u,
p
>
~i.
3.
THE THEOREM
OF
EXISTENCE
OF
GENERALIZED
SOLUTIONS
In this paragraph problem
I
(see
when stagnation zones with residual values
s=
0,l are admitted
in the flow region and thus equation (1.7) can degenerate. In this
case problem
I
is
called degenerative (see remark
3
92).
Theorem 3.1.
At
least one generalized solution
of
degenerative
problem
I
exists under (i
-
iv) being satisfied. This solution
possesses
(in
addition to the definition) the following proper-
ties:
$2)
is
studied in a general case,

Filtration
of
Immiscible Liquids
213
a>o,
q=2+c,
E>0.
The proof
of
the theorem begins with the non-stationary case and
it
will
be carried out in a few steps.
1.
Galerkin approximations in an auxiliary problem
I
We
will
look
for
the approximated solutions
of
an auxiliary prob-
lem
I
in the form
(3.1)
where, fundamental systems
of
functions and in
Y:(Qy1'2)=
{cp(x)
E
(pk,
+1<
E
bi2(Q),
cp(x)=O,
x
E
P2
}
are set in the following way
'Pk
%
'Pi
=
diilc
?
(v
$k,
V(biIQ
=
6ik
(
Sik
are Kronecker symbols).
To
determine the unknown functions
b:
we
get a nonlinear evolution-stationary equation system:
.-
(3.3)
Here
(.,-)
Prove the solvability
of
the problem
(3.21,
(3.3).
In
view of the
made assumptions the coefficients
of
this auxiliary system are con-
tinuous over
a:,bt
functions
pjk,
vk,
CL
are bounded and
pk
being integrated over
t
€10,
21
for all values
a:,
bk.
Substi-
tute
and
(.,
.)I,2
are scalar products in
L(
Q)
and
L,(rj
2
Jk
IU
1
=
c
2;
'pk
+
so
in
pJk
Then to determine
b:
in
each

214
Chapter
5
instant of time we obtain a linear algebraic equation system.Since
due to (i)
S
2
and
+k
being orthogonal
N
N
N
B
jk
gj
Ek=
(K
C
cj
VG.9
C
gkvGk)Q
Z
v(hiyi)
C
Cstt
V
>
0,
v
I
J1
1
then the last one is always solvable and its solution
is
continuo-
usly dependent
on
2:-
Substituting
-9
+
1-
-9
vh
=
-
[K(x,~)
D
(
C
"1:
+,
+
Po>
+
f
(X,Z)]
5vh(
2
9x9
t)
1
in
(3.2)
we are led to the Cauchy problem
of
ordinary differential
equations. The latter, due
t-o
the above mentioned coefficients, is
solvable for
all
t
E
[O,
TI.
2.
Compactness
of
Galerkin's approximations
and
a limit transition
Let's obtain a priori estimates independent of
N
for
s'\'(x,t),
Multiplication
of
(3.2)
by
a:
and integrating of
(3.2)
over
t
results in equalities
over
N
PIT
(x,
tl.
(3.3)
by
b!
followed by
eumming
Let's integrate by parts in the second addend
(3.41,
then with the
help of the Young inequality and the condition (i)
Y
2
from
(3.4)
and
(3.5)
and bearing in mind that
a
1
E
i
=
d,l
(hi
E
h),
-t
and
I
c
vh
I
5
c0
(hi
1,
we come
to
the inequalities
which result in the following estimations:

Filtration
of
Immiscible
Liquids
21
5
--t
k(t)
=
II
BPo
II:,Q
+
IIf
Ili&
and now
it
is
still
assumed that
sot
E
L2(k)
ditions
in
3).
For
an
arbitrary function
v
which turns into
the boundary
r'
inequality
(2.23)s
2
ch.
1
;In
y=qlL
=
-
,
o<CL51
n-
1
n
-2a
and, consequently, from
(3.6)
finally we have
I
(we avoid this con-
zero in
a
part of
is
valid
(3.7)
(3.8)
-#
II
VP'III
5
~(lbi)
(
11
VP,
112,p
+
II
f
II~,Q
+
11
R
11~,r2
2,Q
Assuming in
(3.6)
that
y(t>
f
lIs''(t)
IIZ,n
rential equation
y'(t)
5c,(IVo+
y(t)),
~(0)
=
o
,
we come to the diffe-
from which
and,
f
inally,
We note tha+t fro: the definition of the auxillary problem coeffi-
cients
(
1
F
I
,
If
1
IC(lilhd the variable in
(3.8)
depends only
on
M,
in
(3.9)
it
depends on
id,
E
,
hi but both are independent
of
N.
Now we carry out the finite transition for
+
w
and fixed
E
t
hi-With the estimation
(3.8)
assume
vh
in
(3.2)
to be the
given function (i.e. consider the system
(3.2)
as corresponding to
one parabolic equation). Then, according to the results already
known[
921
the sequence
sense
-
one can
choose
a
subsequence (with the previous designa-
tion)
S"
in wich
s"(x,t)
--t
s(x,t)
almost everywhere
in
Q,
sN(x,
t)
is
compact in the
following
v
sli
-#v
s
is
weak in
L2(d)
and for almost
all
t
(I&'
9
CP),
--t
--t
(ms
9
'p)Q
N
Functions
p
(x,t)
strongly converge on the chosen sequence
then from
(3.3)
we have
s"(x,t).
Actually, let
w
=
pN-
p

216
Chapter
5
N
where
KN=
Ii(x,s
),
K
=Y;(x,s).
Hence
II
vw
112,(i
5
C(Ibl>
(I1
(KN
-
K)
VP
112
2
2
,Q.
-3
(3.11)
since
K,
f
are boundary continuous over a function
(V
P
is
boun-
ded
in
LZ,~
,
and
sN
converge to
s
almost everywhere in
Q.
Multiply each equation (3.2) by
dk(t)
sum
over
k
and Integ-
rate over In the same way each
of
the equatpns
[T3.3)
we multiply by
%
and
sum.
As
a
result
we
get, that
(s
,
p
)
satisfy identities
(2.51,
(2.3) with
+
-
"f
1
-+
0,
t
6
[0,T].
V
V
(pv=
c
dk
(t)
'pk
9
GV
=
c
bk
(/Jk)
1s
V
5
.
1 1
14
For instance, for
s
(x,t)
we obtain the identity
-i
(,Ii,
ph,
CpV)
5
-(us
I'
"Pt
v,
+
(KO
a
v
2
+
E'
9
v
CpV)
-
(c
v
v
sN
)
(pv
)
=
(
mso
cp
>-,
I
-
Q%
(3.12)
-3
vt
'
%
In this identity one can transit to the limit on the sequence
chosen-above
sly
(x,
t>
(
v
is
fixed), since
s",
a(x,s"),?'U,CT'!
(
a,
h;
c are limited) are convergent almost everywhere;
Sn
strongly to
L,(d
all
t.
Thus the limiting function
s(x,t)
will
satisfy the identity
written above
for
all
cp(x,t)
of
the kind
and besides
sN
weakly to
L2(Q)
for almost
V
(3.13)
V
cp
(x,t)
= C
4
'pk
(x),
I
jc_
v
<a
.
1
But these
'pv,(/Jv
are dense
in
Y)ii(G),
Wi(
Q)
Consequently, for
all admitted functions the identities
(2.31,
(2.5)
will
be satis-
fied.
3.
A
priori estimates independent
of
h
In
agreement with the maximum principle proved in
there exist evaluations
0
I
s(x,t>
6
I
(3.14)
and
it
means that
all
integral identities hold with rather initial
than expanded coefficients. Now we obtain a priori
estimates
inde-
pendent
of
h
and
E
using
(3.14).
In the way similar to the proof
of
the maximum principle we come
to the equality
b2
for
s(x,t)
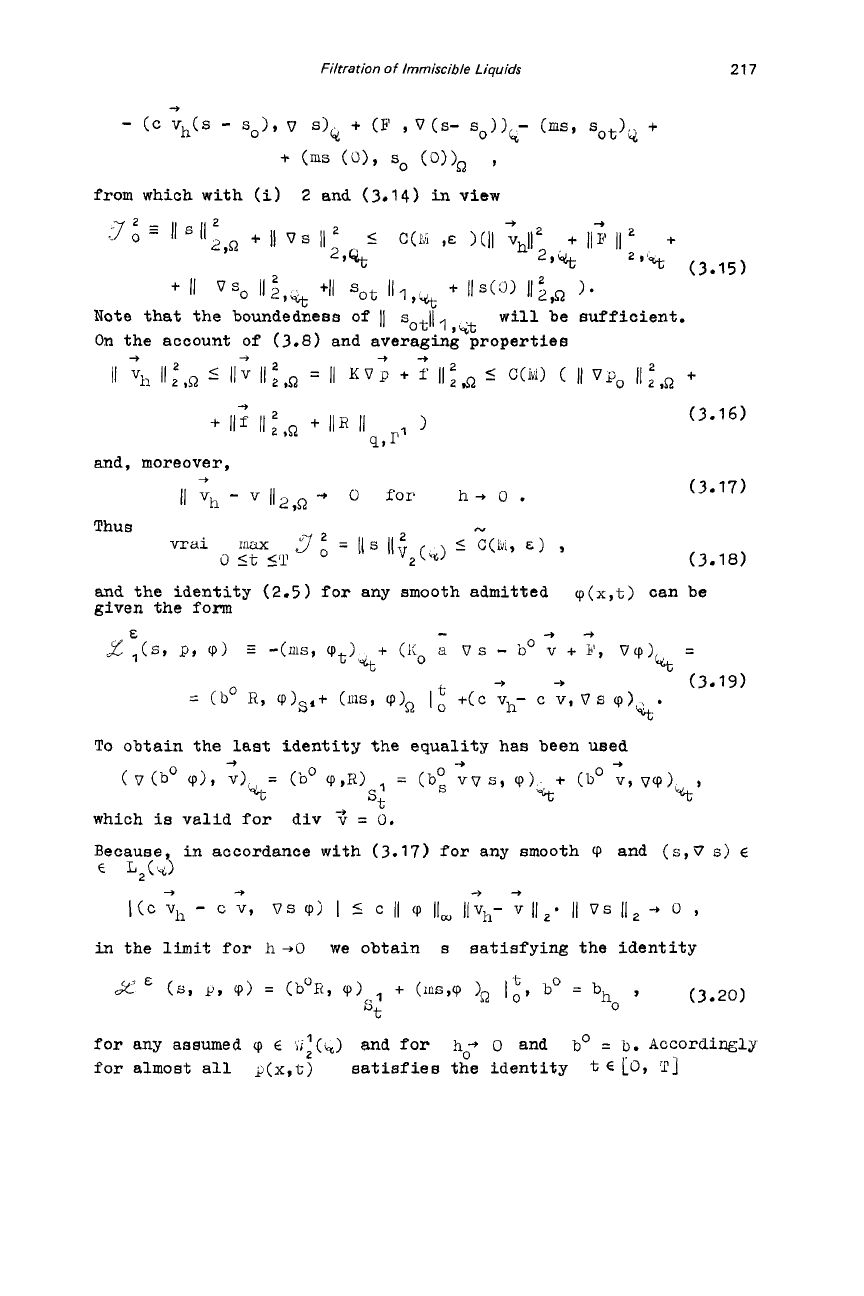
Filtration
of
Immiscible Liquids
217
and, moreover,
--f
11
vh
-
v
1(2,Q
-t
0
for
ht
0
.
and
the identity
(2.5)
for
any smooth admitted
given the form
cp(x,t)
can be
Vcp)%
=
$z
p,
cp>
I
-(rIls,
(4,)
+
(Iio
il
vs
-
b0
V
+
ii',
E
-
33
%
-+
(3.19)
tt
%'
=
(bo
R,
cp)Sd+
(ms,
'PIs1
1,
+(c
vh-
c
V,
V
s
cp)
To
obtain the
last
identity the equality has been used
t
-+
+
(V(bo
cp),
V)
=
(bo
cp,R)
,
=
(bi
VVS,
cp)
+
(bo
v,
vcp)
-+t
%
'
".t
St
which
is
valid for div
"v
=
0.
Because in accordance with
(3.17)
for any smooth
CP
and
(s,J
s)
E
6
L,(J
--f
-9
3t
I(c
Vll
-
c
v9
vs
(4)
I
5
(1
cp
(Icu
IIVh-
v112g
11
OS
112
+
'
2
in
the
limit
for
h-0
we obtain
s
satisfying the identity
t
2
(s,
P,
cp>
=
(b'Ii,
W)
+
(ins,cp
JQ
I,,
bo
=
b
,
(3.20)
for any assumed
cp
E
I,,:(~)
and
for
h;
0
and
bo
=
b.
Accordingly
for almost
all
r(x,t)
satisfies the identity
t
E
LO,
T'J
St
ho
