Antontsev S.N., Kazhikhov A.V., Monakhov V.N. Boundary Value Problems in Mechanics of Nonhomogeneous Fluids
Подождите немного. Документ загружается.


248
Chapter
5
(7.9)
and for
cp
=
s
-
so
the equality respectively
-i
(Keg
0s;
VsJQ
=
-(R,u)
+(
v
v~~,b(s)-
b(so))Q
+
r"
Due to the imbedding compactness
:ii(Q)
Lm(Q)
in
Lq(
Q)
and
L
(I?),
1
5y.
<
my
inequalities (7.10) make
it
possible to choose
ii
sE
from
sequences
almost everywhere in
8
and on
I'
which derivatives weakly converge
to
L
(Q).On these subsequences similar to
4,
~3
one can transit to
the
limit
for
E
--f
0
and thus, finally complete the proof of the
theorem.
2.
Choice of other searched functions
It
is
often convenient due to the degenerating character
of
equa-
tion (1.7) to use another pair of unknown functions instead of
s
and
p.
For
this purpose one can choose potentials
9,=p,+
pi
Ji
,
(p
&(XI,
u
E(-<)=
I
blio2d
<)subsequences converging
0
2
--
i=
1
,
2
satisfying the following boundary problem equivalent
to
(7.1
1,
17.2):
3
+-+
uiv(iii
v
si>
a-AV
vi
=
o;G~~
I,2
=
QI~
,
vi
n
--
koL
H
y
lY1
-
k
i
=
I,
2.
(7.11)
s= s(
G,
,
0
)
is
clearly defined from the rela-
Here, dependence
tion (see
1.1
)
Yc(",s)
=
P2-
iJl
=
Q2-
C,
+
gh(
P2
-
PI
)
y
(7.12)
a
P,
since according to the assumption
(i)
s.2
I
as
-
I
>
0.
The second of the previous couple of searched functions
is
restored

Filtration
of
Immiscible Liquids
249
by the formula
La
=
Q
1
Note that from
(7.73)
the
know
values
I’*
c
an
and
s=so,
p=p,
on
the
is
defined, then from (7.12) and surface
from
(7.13)
G: .
In some cases
it
is
sufficient to change only one unknown function
SO:)
on
any of the potentials
a.
adding to
the
respective equa-
lities (7.1) (for
i
=
1
or
2)
relations (7.2) for
p(x)
l
3.
Regular generalized solutions
Generalized solutions
of
the problem
(7.11,
(7.21,
for which in-
equalities occur
-
2
<
6,
i
&(x)
51-
6,
<
1,
XE
a
,
will
be called regular. Existence
of
such solutions
is
provided
from the theorem 1.1 by satisfying conditions (2.7)
of
problem
regularity.
For
regular solutions
and
(d
E
,J’(
n)
.
Investi ating the smoothness of regular generalized solutions
(7.11,
v7.2)
in
is
convenient to pass over
to
the unknown func-
tions
uniformity elliptic and their coefficients depend on
x,
and
through
s
on
gj2-
v1
.
Theorem 7.2. Let
W
=
(5,
1.1
be
a
regular generalized solution of
the problem (7.11, (7.2), in addition
to
the condition of the
theorem 7.1 the assumption being satisfied
-
ll
of the equation
(l.l@)
(yIL
=
~y~~
-
=
13
)
for vhich are
(vj
I
=
1”
u
I2
E
1.2
,
I’,(x>
E
C(
a)

250
Chapter
5
then
in
the region
Q
b
={x:x~~,
rninlx-y1>_6>0, y~r''nr*)
evaluations
occw
Proof. Let
?2
=
(
Ql
,
Qi,,)be
a
searched vector-function, satiefying
the boundary problem (7.11). Since each of the potentials
nuity of
smoothness of function pc(x,s>
follows a Hb'lder continuity
of
w(x)
=
(s(x), p(x)>. Therefore
tLi[x,s(x)]
E
C
"(
8)
and from the theorem
4.3
V
(Pi
E
L
(
Q'),
5'
c
Q,
I
<
y<m
and
Vmi
E
L
(a),
1
<
%<uin(q,
y-d
n
).
Qi
Y
i
=
1,
2, satisfies the same problem as
p(x>
the IIb'lder conti-
from relations (7.121, (7.13)
it
~~(2:) results from the theorem
4.1.
Then becRuse of the
9
il
cLlroi
VS
4
koi
VI<~
E
Ly(
a')
(Lq
(
Q))
Now
v
K.
=
i<
O
ds
and consequently theorem
4.3
yields that
Qi
E
i/'(
H)
and
so
on.
4.
Degenerating case
Introduce
in
equations (7.11, (7.2)
a
new unknown function
J(X)
connected with
s(x)
by relations
S
j
a.
(
g)d
gzu(s),
s
=
u
0
4
-1
(7.17)
u
=
(u)
=
s(ii)
,
u.
as
where
ao(s)
=
-];I
.Now
the equalities (7.1) take the form
-
-t
+
j-9
div(
ii0
vu
+
i';
)
E
-div
v4
=
0,
u
1
,2=
uo
'
vnlI1
(7.18)
-
-
*
--f
where
Theorem 7.3. Let
0
5
s(x)
51
and in addition to the assumptions
(i, ii)
from
9
2
we have
Lo
(x)
=
ito
[pc
1-l
,
I&
=
I:,
vp
+
fo
.
(vii)
~(x)
E
L~(I~'
>,
r
>
n
-I;
wo(x)
E
.Jil(
I-,'
),
9
y
>n
,
r
E
MI,
and in the equality (7.17)
s(u)
EC
B~O,u(l)],
@
>
0
(for the
latter
it is
enough to demand
that
ao(s)
LC
s
"(1-s)
p,
(C,
v,p>
>
>O)
Then
in
a
two-dimensional case n
=
2
any generalized solution
in
u'xi
only
if
the additional condition
is
satisfied
of the problem (7.11, (7.2)
is
continuous due to Holder
and in
a
three-dimensional case n
=
3
this fact
is
valid

Filtration
of
Immiscible Liquids
25
1
sup
lK(s)
-
Ilh,
<
1,
(7.19)
Ylhereh3(A2
case only one-sided degeneration of the problem (i.e.
for
0
5
s
5
51-6,
<
1
or
0
<
b0
5
s
5
I).
Proof. Notice beforehand that the function
u(x)
introduced by the
formular (7.17) together with
p(x)
is
a
generalized solution of
the problem (7.141,
(8.18).
Here d5e to theorems
4.1,
4.2
p
E
6
C
cI(z)
n
and with then
I?*
E
Ly(h),q
>
2.
In accordance
with '$he theorem 7.1 for
a
lIglder continuity
u(x)
it
is
sufficient
that
E
L
6)
,il
>.
n.
Consequenly for
n
=
2
this condition
is
satisfied.
Fbr
the inequality to be true
y
>
2
for
n
=
j
by
the
theorem 4.2 ch.
I11
the condition (7.19) must be satisfied.
Now
let saturation
s(x)
in the problem being considered reach
only
one
of the finite values
0
or
1
(for exactness
0
<
6,
5
s
5
I).
Then considering the boundary problem
(7.21,
(7.11) for
I
=
1
and
for
(Q,,
i;)
satisfying uniformly elliptic equation system,
ve obtain similarly to the previous, that
(Ql(x),
l>(x))
E
C
@(E)
and in the case whenn
=
3
without any additional condition (7.19).
The
theorem has been proved.
5.
Uniqueness
of
regular solutions
Theorem
7.4.
Let the assumptions
(v)
of
the
theorem 4.2 be
satis-
fied and
=
1)
is
a constant
in
inequality (4.15) or in the
Iq(Q)
++
Ibs,
Is,
.Lost
iCS'
Kqs
1
5
6
(7.20)
Then
a
regular generalized solution
w
=
(6,
y)
of the problem
(7.11,
(7.2)
is
unique,
if
(7.21)
where
C,
and
XI
are constants in inequality
(7.15).
C
is
a
con-
stant in
(2.23)
J
2
ch.
1
with
a
=
1
and
p
2
IFo,
K,
Iill
and
regular generalized solutions
of
the problem and
u
=
ul
-
up,
p=p
-
p,.
Then subtracting the integral identities (2.2*),
(2.3*) which correspond them from each other we come to the equa-
lities
-3 -3
(KO
v
u
+
GU
+
Kl(U1)O
p,
VqQQ
=
(h,
cp)
(7.22)
r1

252
Chapter
5
(7.23)
Here+
~
-b
-b
GU
=
Af
0
+
AH,Vp,,
1)U
=
AKV
P,
+
Afl
BU
=
-
R
Abl
(7.24)
where
Af(u)
=
f(u,)
-
f(u,).
Assuming
further that
with the help of the
Young
inequalities from (7.221, (7.23) find
that
cp
=
U)
J,
=
Q
n
1
+
I
vp21
E
z,
But bearing in mind (2.23)
g
2
ch.
1
and
consequently
On
the other hand due to (7.151, (7.21)
k,
5
8,
<
1.
V
u
E
O(
v
s
0)
and
it
means
u
=
s
E
0.
From
(7.25)
similar
assumption
is
true
for
p.
ilemark 1.
As
it
is
seen from (7.25)
for
b
5
0
(B
5
0)
one cen
deny
Remark
2.
It
is
easy to aee that the ine uality (7.21) always
holds for
a
"weakly related" system (7.17, (7.21,
i.e.
for
6
>
0
being
mall
in
the inequality (7.20).
Therefore
the condition (7.20) on
lbsl
8.
FURTHER
SMOOTHNESS
OF
REGULAR NON-STATIOI'JARY
PROBLZLI SOLUTIONS
1.
Introduction
This paragraph investigates further smoothness of generalized
so-
lutions
(6.4)
s(x,
t),
p(~,
t)
of an initial-boundary problem (6.1)
-
-b
L,s
=
-
inst
+
div(KoaV
s
+
%,
V
p
+
fo)
=
0,
(8.1)
-b
L2p
5
div(kVp
+
f)
=
0, (x,
i;)
E
Q
=
52
x
(0,
T),
(8.2)

Filtration
of
Immiscible
Liquids
253
++
-+-+
(I<
vp
+
f)n
=
-R(x,
t),
(Koa
0s
+
K,
vp
+
fo)n
=
-
bH,
(x,
t)
E
sl.
(8.4)
-+
n
-
normal to
r
1
(8.5)
which coefficients are defined by formulas
(1.19)
9
1
ch.
1
and
satisfy the conditions (i)
-
(iv)
9
2
(of
existence
of
a
generali-
zed solution).
The properties
of
the smoothness of a summed filtration velocity
with a given saturation field and vice versa have been studied
in
4,
5.
Due
to
the peculiarities
of
the initial system (8.1),
(8.2)
(degenerating equation
for
S(X,
t)
and absence of
a
temporal
derivative
of
i~(X.,
*))investigations of each
of
these rather com-
plicated problems make
it
possible
to
study rather completely the
cmoothness
of
solutions
of
a
joint
regular, non-stationary problem
for
11
=
2
(see
Y
6).
However just for
n
=
3
consecutive conside-
ration of separate problems leads to the existence of strong (in-
cluding classical) solutions only
in
flsmalll'
over
t
or
for
small
fluctuation of the function
k
=
kol
+
ko2
.In accordance with the
theorems
6.1
-
5.4
the smoothness
of
generalized solutions
of
a
joint non-stationary problem
for
n
2
3
is
determined inside the
region
Q
only by the smoothness of system coefficients, and res-
pectively in also by the smoothness
of
the boundary condi-
tions, if in this solution
s(x,
t)
is
continuous due to Holder
over
a
variable
x.
In this paragraph Holder estimates
s(x,
L)
over a variable
x
and evaluations
of
all
derivatives
of
the
so-
lution for nny finite
t
E
[O,
?]entering the system are establi-
shed in the present paragraph. Further propertLes of the smooth-
ness of
a
solution now results from
YG.
Stability with respect
to
the boundary values, uniqueness and asymptotic behaviour of regu-
lar solutions of a joint problem are psrellely investigated.
2.
fiuiliary evaluations and inequalities
I-:ere some specific inequalities are dpresented and estimates
of
hieher derivatives of "reduced" pressure
p(~,
L)
with
the deri-
vatives of saturation
s(x,
t)
Ere established.
Lemma
8.1.
(92,
page
111).
Let
u(x)
be a boundary function from
product u
5
turns into zero in the boundary
P
of the region
a.
Then
di(Q)
n
sViu+2
(a),
u
2
O,~(X)
is
a smooth function such that the
The last term being bounded by the
Young
inequality,
(8.6)
takes
one of the following
forms
:

254
Chaprer
5
2(V+l)
-2v
6
v+l
x
(32v-
IV
5,
5
Idx,
(8.7)
Further the inequality
U+l
2
V+l
v+l I-v
Q
I
Iuxyl
5
dx
5
C
Q
I
{lA
ulV+'5'
+
bXI
15,l
5
+
+
l~lv+'~15x12V+25-2~
+
1<,1
v+l
<
I-v
)
}dX,
(8.8)
will
be often used, where
C
=
C(Q,
v).
Now consider the equation (8.2) dependent on the parameter
t
E
LO,
J]
the function
s(x,
t)
in a sphere
u
=
{x:(x,
x,)
E
Q,
Ix
-
xol
<
p}
c
Q.
Assume that in (8.2) coefficients,
a
given func-
tion
s(x,
C)
and a solution
p(x,
t)
are rather smooth functions
of their arguments.
Lemma 8.2. Let
p(x,
t)
be
a
boundary solution(lp1
5
hi)
of
the
equation
(8.2).
Its
coefficients satisfy the conditions
P
0
<
P-'
5
((KO
5,
5)/
Ill2,
k)
5
CL
<
m,
(8.9)
(8.10)
-B
IIfllq,m,c
5
1\19
9
>
no
Then for
p(x,
t)
the estimate
is
valid with
some
9'
>
2,
>
0
and
a
constant
C,
dependent
only on
P,
iu
and on the distance from
52'
to
rT
The proof results directly from the theorem 4.1, 4.2.
Lemma
8.3.
Let in addition to
(0.91,
(8.10)
(lk;I,
llKo
IlC(Q))
5
k*
(8.12)
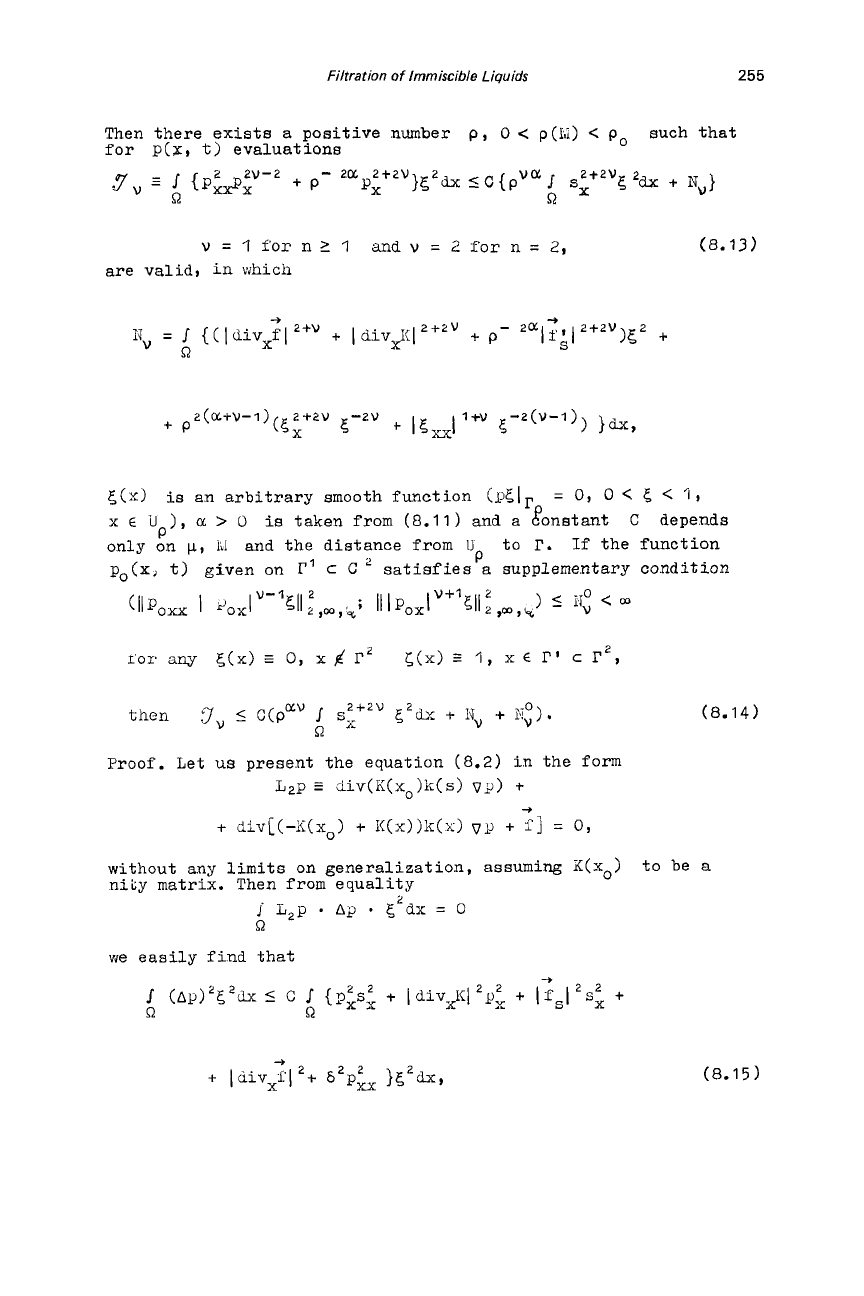
Filtration
of
Immiscible Liquids
255
Then there exists
a
positive number
p,
0
<
p(1i)
<
po
for
p(x,
t)
evaluations
such that
5
dx
+
Nu)
yv
5
I
{P&y
+
p
B,
}$dx
C_C{pV"J
2+2v
-
20:
2+2v
Q
s2
sx
v=Iforn>l
a.ndv=;!f'orn=Z,
are valid,
in
which
(8.13)
I&,
l+v
<-2(v-1>
+
p2(cL+v-1)
(<:+2V
5-2v
f
l<,l
<(XI
is
an arbitrary smooth function
(Ug1
=
0,
0
<
5
<
I,
x
E
il
),
0:
>
0
is
taken from
(8.11)
and argonstant
C
depends
only on
p,
bl
and the distance from
u
to
I?.
If
the function
po(x,
t) given on
I"
c
C
'
satisfies
a
supplementary condition
P
P
5
i1:
<
m
(8.14)
Proof. Let us present the equation
(8.2)
in
the form
L2p
E
div(K(x,jk(s)
02)
+
+
+
div[(-X(xo)
+
IC(x))k(x)
vp
+
€1
=
0,
without any
limits
on generalization, assuming
X(xo)
niLy matrix. Then from equality
Q
to be
a
j
~,p
.
~p
.
c'dx
=
o
we easily find that
-+
I
(~p)'<~ilx
5
c
I
{pis:
+
IdivxI<12pt
...
+
(fS12si
+
Q
B
(8.15)

256
Chapter
5
where
c
=
c(p,
1%;)
and
6(P)
=
ma
IK(xo)
-
K(x)l
.The
first
three
addends in the right side
(8.15)
are estimated by the Chauchy in-
equality with random
E
>
0
in the following way:
2PX
SX
I
ES;
+
E
21
div
Kl
p,
I
p,
+
I
div
i;14,
22
-1
4
22
4
d,,
Applying further inequalities
(8.17)
Now
assuming
E
=
p"and choosing
p
to be too small to satisfy
the inequality
2C,(P"('I
+
p")
+
b2>
5
1,
due
to
(8.161,
(8.17)
and we come to the necessary estimate
(8.13)
with
u
=
1
To
prove the estimate up
to
the boundary
it
is
enough
to use insteRd of
(8.16)
the inequality
with
5
#
0
In the case
of
v
=
2
one must consider in the similar way the
inequality
on
P.
The
last
one
is
a
consequence
(8.8)
for
u=p-
lJo
and use
(8.7)
after integrating by parts with
u
=
2.
The lemma
has been proved.

Filtration
of
Immiscible Liquids
257
3.
Continuity
of
regular solutions
by
Halder
We'll assume the coefficients
of
the system
(8.11,
(8.2)
to
posses
the properties
(8.19)
(8.20)
In
accordance with lemma 2 conditions (8.20) and (8.18) on
Lo,
1.;
provide bounds
for
with some
(1'
>
2
and a constant
C
dependent
on
p,
id,
llpl[m,k
and the distance
from
Q
to
r.
Using (8.2) give equation
(8.1)
the
form
-
--t+
L
s
z
-st
+
div(iCavs
+
A)
+
'3vs
+
g
+
Dvsvp
=
0
(8.23)
++-3-+-t+
+
Here
-
~14(
=
KO,
-A
=
A,
+
K2,
'
InAl
-
-
I'o,
rail,
=
-
bf,
=
vmz
.
To,
lAL6
=
-bi'VU,
1liD
=
b'
I(.
--f
->
-,
-9
--f
-9-9
-3
-3
I!
=
iij
+
Lib,
LI'A~
=
K
~VIU,
i~h
=
-bi
i;,
=
li,
+
A6,
-3
-3
-+
+
L12il
s
It
is
easy
to
verify that due to (8.18)
-
(8.20) coefficients
(8.23) satisfy the conditions
P-%
5
(Ea
(;>/1512,
5
p2,
(8.24)
(IIqI,
,r
,
*9
*
llum'~)
5
C(lU.9
PI,
(8.25
in which
q
r
j
=
1,
4
are connected by relations (8.21 and
for
j
=
5,
6
by equalities
-
JJ
J'
J'
l/r
+
n/2ciJ
=
I
-
xJ,o
<
x
<
(8.26)
PTotice that
for
n
=
2
according
to
the first of the inequalities
(8.22)
p,
E
L
(%),
(1'
>
2
and for
a
coefficient
D
vp (8.21)
is
satisfied. These conditions on coefficients
of
the equation
(8.23)
(X,
A,
B,
g,Dvp)
are considered
as
being given functions)
3
J
Y
