Антонова Н.Б., Вечер А.В. Прогнозирование и планирование экономики
Подождите немного. Документ загружается.

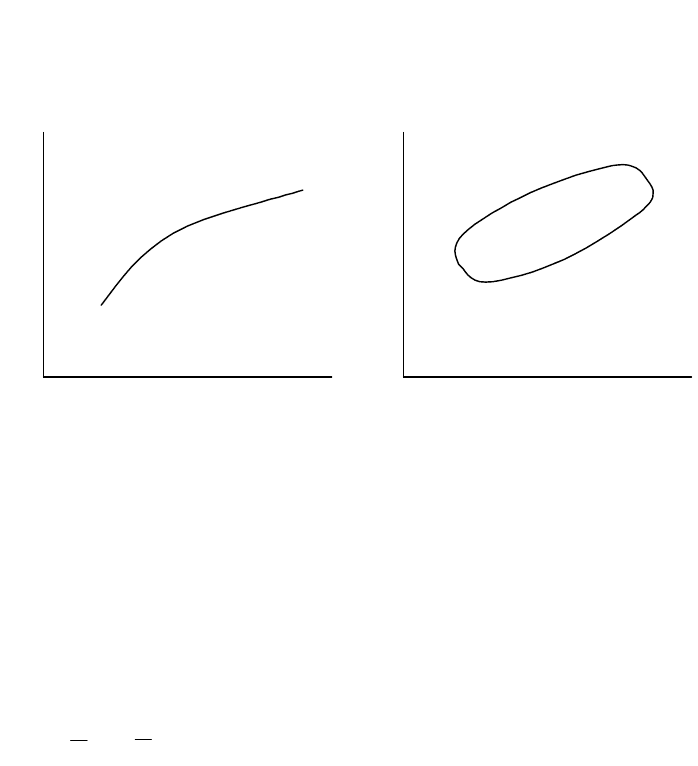
Будем обозначать искомую прогнозируемую величину
через У и называть зависимость переменной, а влияющие на нее
переменную через Х и называть независимой переменной.
Связь между зависимой и независимой переменными может
быть функциональная, в этом случае каждому значению
независимой переменной соответствует одно определенное
значение зависимой переменной, графически такая связь
выражается линией на графике. Второй вид связи –
вероятностная (стохастическая) связь, в этом случае одному
значению независимой переменной соответствует несколько
значений зависимой переменной. Графически вероятностная
связь может быть представлена как некое облако точек (рис.12).
Причем частота появления различных значений переменной Y
при одном и том же значении
i
x
подчиняется какому-то закону,
т.е. имеет определенный тип распределения, одинаковый во всем
диапазоне значений независимой переменной.
x
y
x
y
Рис.12. Функциональная (а) вероятностная (б) связь
переменных.
Для описания вероятностной связи переменных
используются уравнение регрессии. В идеологии регрессионного
анализа лежит представление о всех возможных значениях
переменных Х и У как о случайных отклонениях от их средних
значений
x
и
y
. Регрессионное уравнение устанавливает связь
между отклонениями зависимой и независимой переменных от
своих средних значений. Следует особо отметить, что в
101

регрессионном анализе речь идет именно о связи (определенной
степени совместности изменения) Y и X, а не зависимости Y от
X. Иными словами регрессионный анализ не устанавливает факт
влияния X на Y, фактически это может быть и противоположное
влияние - Y влияет на X, или обе переменные Y и X зависят от
третьей или третьих переменных. Во всех этих случаях будет
наблюдаться некоторая согласованность изменения значений X и
Y, и эту согласованность можно установить с помощью
уравнения регрессии.
Термин регрессия был введен в позапрошлом веке в
результате изучения влияния роста родителей на рост детей.
Повсеместно бытует мнение, что у высоких родителей высокие
дети. Проверка на большом статистическом материале показала,
что в среднем дети высоких родителей имеют рост меньший, чем
рост родителей, т.е. рост детей высоких родителей регрессирует,
имеет тенденцию возвращаться к среднему росту. А рост детей
невысоких родителей прогрессирует – имеет тенденцию
приближаться к среднему росту.
Наиболее часто на практике для описания связи между X и
Y применяется линейный закон. Соответственно говорят о
парной линейной регрессионной зависимости, с ее помощью
взаимосвязь между зависимой и независимой переменными
описывается следующим образом:
xy *
где:
,
- коэффициенты регрессионного уравнения;
- остаточный член.
Таким образом, случайная величина Y представляется
состоящей из двух частей:
теоретического значения, которое можно рассчитать по
известному значению X с использованием формулы
xy *
;
и остаточного члена
который представляет собой
случайную составляющую которую предсказать невозможно и
102

благодаря которой связь между зависимой и независимой
переменными носит вероятностный характер.
Среди причин появления случайной составляющей
могут
быть следующие:
- отсутствие в уравнении регрессии других независимых
переменных влияющих на зависимую переменную и не
включенных в уравнение вследствие их незнания или отсутствия
возможности надежного измерения;
- агрегирование зависимой переменной из нескольких
однородных, но все-таки отличающихся друг от друга
переменных (прибыль по предприятию представляет собой
сумму прибыли по отдельным продуктам производимым этим
предприятием, а это схожие, но все-таки разные экономические
категории);
- несоответствие избранной теоретической зависимости
между зависимой и независимой переменной фактической
зависимости;
- ошибки измерения как зависимой, так и независимой
переменных.
Во всех этих случаях возникают ошибки, которые приводят
к возникновению случайной составляющей.
Общая схема прогнозирования с использованием
регрессионной зависимости выглядит следующим образом. По
имеющемуся набору
n
пар значений
i
y
и
i
x
необходимо найти
параметры уравнения регрессии, а затем с помощью
полученного уравнения и нового значения независимой
переменной
1n
x
, рассчитать прогнозное значение зависимой
переменной
1n
y
. Поскольку при этом случайную составляющую
предсказать не удается, то дополнительно необходимо оценить
точность полученного прогноза.
Оценка параметров уравнения регрессии
103

Для прогнозирования с помощью уравнения регрессии
необходимо вычислить коэффициенты
и
уравнения
регрессии. И здесь существует еще одна проблема
сказывающаяся на точности прогнозирования. Она заключается
в том, что обычно нет всех возможных значений переменных Х и
У, т.е. генеральная совокупность совместного распределения в
задачах прогнозирования не известна, известна только выборка
из этой генеральной совокупности. В результате этого при
прогнозировании помимо случайной составляющей возникает
еще один источник ошибок – ошибки, вызванные не полным
соответствием выборки генеральной совокупности и
порождаемыми этим погрешностями в определении
коэффициентов уравнения регрессии.
Иными словами вследствие того, что генеральная
совокупность не известна, точные значения коэффициентов
и
уравнения регрессии определить не возможно. Используя
выборку из этой неизвестной генеральной совокупности можно
лишь получить оценки
a
и
b
истинных коэффициентов
и
.
Для того чтобы ошибки прогнозирования в результате
такой замены были минимальными, оценку необходимо
осуществлять методом который гарантирует несмещенность и
эффективность полученных значений. Метод обеспечивает
несмещенные оценки, если при неоднократном его повторении
с новыми выборками из одной и той же генеральной
совокупности обеспечивается выполнение условия
a
и
b
.
Метод обеспечивает эффективные оценки, если при
неоднократном его повторении с новыми выборками из одной и
той же генеральной совокупности обеспечивается минимальная
дисперсия коэффициентов a и b, т.е. выполняются условия
min
2
a
и
min
2
b
.
В теории вероятности доказана теорема согласно которой
эффективность и несмещенность оценок коэффициентов
104

уравнения линейной регрессии по данным выборки
обеспечивается при применении метода наименьших квадратов.
Суть метода наименьших квадратов заключается в
следующем. Для каждой из
n
точек выборки записываются
уравнение вида
i
xba
i
y
*
. Затем находятся ошибка
i
e
между
расчетным и фактическим значениями
i
y
i
y
i
e
. Решение
оптимизационной задачи по нахождению таких значений
a
и
b
которые обеспечивают минимальную сумму квадратов ошибок
для всех n точек, т.е. решение задачи поиска
min
2
)(
i
e
, дает
несмещенные и эффективные оценки коэффициентов
и
.
Для случая парной линейной регрессии это решение имеет вид:
2
)(
))((
x
i
x
y
i
yx
i
x
b
xbya *
Следует отметить, что полученные таким образом по
выборке несмещенные и эффективные оценки истинных
значений коэффициентов регрессии для генеральной
совокупности вовсе не гарантируют от ошибки при однократном
применении. Гарантия заключается в том, что, в итоге
многократного повторения этой операции с другими выборками
из той же генеральной совокупности, гарантирована меньшая
сумма ошибок по сравнению любым другим способом и разброс
этих ошибок будет минимален.
Полученные коэффициенты уравнения регрессии
определяют положение регрессионной прямой, она является
главной осью облака образованного точками исходной выборки.
Оба коэффициента имеют вполне определенный смысл.
Коэффициент
a
показывает значение
y
при
0x
, но в многих
случаях
0x
не имеет смысла, кроме того часто
0a
также не
имеет смысла, по этому приведенной трактовкой коэффициента
a
нужно пользоваться осторожно. Более универсальная
трактовка смысла
a
заключается в следующем. Если
0a
, то
относительное изменение независимой переменной (изменение в
105

процентах) всегда меньше чем относительное изменение
зависимой переменной.
Коэффициент
b
показывает насколько единиц изменится
зависимая переменная при изменении независимой переменной
на одну единицу. Коэффициент
b
часто называют
коэффициентом регрессии подчеркивая этим, что он важнее чем
a
. В частности, если вместо значений зависимой и независимой
переменных взять их отклонения от своих средних значений, то
уравнение регрессии преобразуется к виду
)( x
i
xby
i
y
.
Иными словами в системе преобразованных координат любая
линия регрессии проходит через начало координат (рис 13) и
коэффициент
a
отсутствует.
x
y
xx
i
yy
i
x
y
Рис 13. Положение регрессионной зависимости в системе
преобразованных координат.
Параметры уравнения регрессии говорят нам о том, как
связаны между собой зависимая и независимая переменная, но
ничего не говорят о степени тесноты связи, т.е. показывают
положение главной оси облака данных, но не ничего не говорит
о степени тесноты связи (насколько узко или широко облако).
О степени тесноты связи можно судить по линейному
коэффициенту корреляции
xy
r
:
2
2
y
x
b
xy
r
Коэффициент корреляции меняется в пределах от –1 до +1.
Чем он ближе по абсолютному значению к единице, тем сильнее
зависимость (тем сильнее облако данных прижато к своей
106
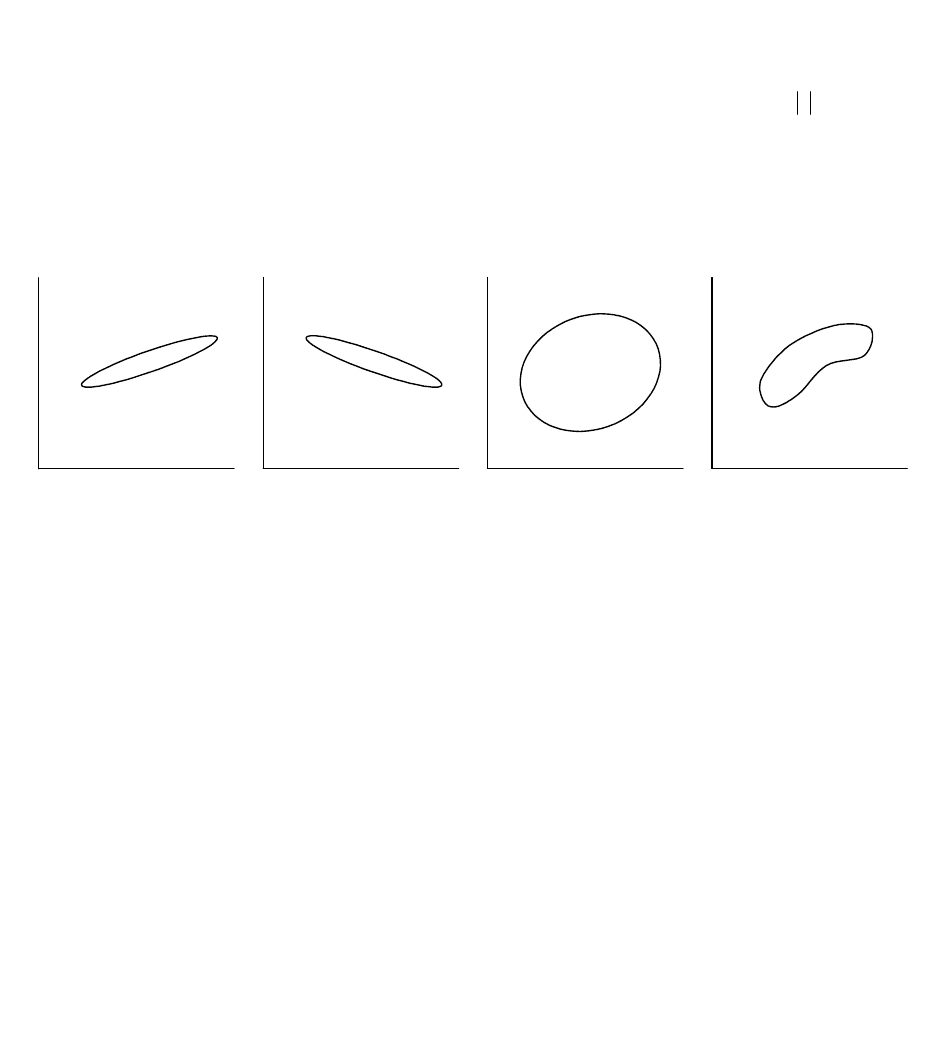
главной оси). Если
0
xy
r
то наклон линии регрессии
отрицателен, чем ближе он к 0 тем слабее связь, при
0
xy
r
линейной связи между переменными нет, а при
1
xy
r
связь
переменных является функциональной. Влияние коэффициента
корреляции на форму и положения облака данных
проиллюстрировано на рис 14.
x
y
1
xy
r
x
y
1
xy
r
x
y
0
xy
r
x
y
xy
r
не имеет
смысла
Рис 14. Влияние формы и положения облака данных на
парный линейный коэффициент корреляции.
Коэффициент корреляции позволяет получить оценку
точности уравнения регрессии - коэффициент детерминации
2
R
. Для парной линейной регрессии он равен квадрату
коэффициента корреляции, для многомерной или нелинейной
регрессии его определение сложнее. Коэффициент детерминации
2
R
показывает, сколько процентов дисперсии зависимой
переменной объясняется уравнением регрессии, а
2
1 R
- сколько
процентов дисперсии осталась необъясненной (зависит от
неконтролируемого нами случайного члена
).
Проверка значимости уравнения регрессии
После того как уравнение регрессии построено и с
помощью коэффициента детерминации оценена его точность,
остается открытым вопрос за счет чего достигнута эта точность
и соответственно можно ли этому уравнению доверять. Дело в
том, что уравнение регрессии строилось не по генеральной
совокупности, которая неизвестна, а по выборке из нее. Точки из
107
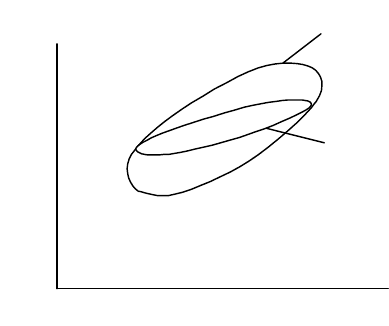
генеральной совокупности попадают в выборку случайным
образом, по этому в соответствии с теорией вероятности среди
прочих случаев возможен вариант, когда выборка из “широкой”
генеральной совокупности окажется “узкой” (рис. 15).
x
y
генеральная совакупность
выборка
Рис. 15. Возможный вариант попадания точек в выборку из
генеральной совокупности.
В этом случае:
а) уравнение регрессии, построенное по выборке, может
значительно отличаться от уравнения регрессии для генеральной
совокупности, что приведет к ошибкам прогноза;
б) коэффициент детерминации и другие характеристики
точности окажутся неоправданно высокими и будут вводить в
заблуждение о прогнозных качествах уравнения.
В предельном случае не исключен вариант, когда из
генеральной совокупности представляющей собой облако с
главной осью параллельной горизонтальной оси (отсутствует
связь между переменными) за счет случайного отбора будет
получена выборка, главная ось которой окажется наклоненной к
оси. Таким образом, попытки прогнозировать очередные
значения генеральной совокупности опираясь на данные
выборки из нее чреваты не только ошибками в оценке силы и
направления связи между зависимой и независимой
переменными, но и опасностью найти связь между переменными
там, где на самом деле ее нет.
108

В условиях отсутствия информации обо всех точках
генеральной совокупности единственный способ уменьшить
ошибки в первом случае заключается в использовании при
оценке коэффициентов уравнения регрессии метода,
обеспечивающего их несмещенность и эффективность. А
вероятность наступления второго случая может быть
значительно снижена благодаря тому, что априори известно одно
свойство генеральной совокупности с двумя независимыми друг
от друга переменными – в ней отсутствует именно эта связь.
Достигается это снижение за счет проверки статистической
значимости полученного уравнения регрессии.
Один из наиболее часто используемых вариантов проверки
заключается в следующем. Для полученного уравнения
регрессии определяется
F
-статистика - характеристика
точности уравнения регрессии, представляющая собой
отношение той части дисперсии зависимой переменной которая
объяснена уравнением регрессии к необъясненной (остаточной)
части дисперсии. Уравнение для определения
F
-статистики в
случае многомерной регрессии имеет вид:
))1/(
2
)((
)/)
2
)((
mn
i
y
i
y
my
i
y
F
где:
m
y
i
y
2
)(
- объясненная дисперсия - часть дисперсии
зависимой переменной Y которая объяснена уравнением
регрессии;
1
2
)(
mn
i
y
i
y
- остаточная дисперсия - часть дисперсии
зависимой переменной Y которая не объяснена уравнением
регрессии, ее наличие является следствием действия случайной
составляющей;
n
- число точек в выборке;
m
- число переменных в уравнении регрессии.
109

Как видно из приведенной формулы, дисперсии
определяются как частное от деления соответствующей суммы
квадратов на число степеней свободы. Число степеней свободы
это минимально необходимое число значений зависимой
переменной, которых достаточно для получения искомой
характеристики выборки и которые могут свободно
варьироваться с учетом того, что для этой выборки известны все
другие величины, используемые для расчета искомой
характеристики.
Для получения остаточной дисперсии необходимы
коэффициенты уравнения регрессии. В случае парной линейной
регрессии коэффициентов два, по этому в соответствии с
формулой (принимая
1m
) число степеней свободы равно
2n
.
Имеется в виду, что для определения остаточной дисперсии
достаточно знать коэффициенты уравнения регрессии и только
2n
значений зависимой переменной из выборки. Оставшиеся
два значения могут быть вычислены на основании этих данных,
а значит, не являются свободно варьируемыми.
Для вычисления объясненной дисперсии значений
зависимой переменной вообще не требуются, так как ее можно
вычислить, зная коэффициенты регрессии при независимых
переменных и дисперсию независимой переменной. Для того
чтобы убедиться в этом, достаточно вспомнить приводившееся
ранее выражение
)( x
i
xby
i
y
. По этому число степеней
свободы для остаточной дисперсии равно числу независимых
переменных в уравнении регрессии (для парной линейной
регрессии
1m
).
В результате
F
-критерий для уравнения парной линейной
регрессии определяется по формуле:
))2/(
2
)((
)
2
)(
n
i
y
i
y
y
i
y
F
.
В теории вероятности доказано, что
F
-критерий уравнения
регрессии, полученного для выборки из генеральной
110
