Ames W.F., Harrel E.M., Herod J.V. (editors). Differential Equations with Applications to Mathematical Physics
Подождите немного. Документ загружается.


120
F.
Gesztesy
&
R.
Weikard
(4.24)
becomes
(4.28)
QI
=
(XI,
-61
Ikin+l(XI
+
iO)”2J)
61
E
{t,
->,
1
5
1
I
N.
In this particular contest it can be shown that
(4.23)-(4.25)
extend
to the case
AN
5
Eo
(in addition to
(4.22)).
The single commutation method has the obvious drawback that
A1
in
(4.15)
is confined to being below
EO
=
inf[a(IIo)] since for
A1
>
inf[a(Ho)],
$0
in
(4.17)’ (4.19)
would have at least one zero by
Sturm’s oscillation theory and hence
Vl
in
(4.19)
would necessarily be
singular.
In
order to overcome this drawback and insert an eigenvalue
A1
into any spectral ga.p
of
If0
one is led to the double commutation
method (going back at least to [23] and described in detail in
[13],
[14], [22], [25-271,
[38]),
a
refinement
of
two
single commutations
at
the same spectral point
XI.
Assuming
one factors again
A1
E
R\o(Ho)
(4.29)
(4.30)

Spectral Deformations and Soliton Equations
121
$O,*Pl,.)
E
L2((K
*4>,
E
IR,
Ho
$O,*,(Al)
=
A1
$O,*(Al)
and
V1,*
are now singular in general. Introducing
@f(4
=
q1,*(4/%,*(4?
(4.35)
B*
=
-
d
+
a*,
Bf
=
--
d
+
a*,
(4.36)
dx dx
one infers
by
inspection that
A
further commuta.tion of
Bh
and
Bf
then leads to
(4.38)
+
Vrl,*
is in the limit point case
d2
One can prove that
T?],*
=
--
dx2
at foo and that
Hence
71,k
E
(0,oo)
represents the non-isospectral case. The
two
cases
71,k
=
0,oo
on the other hand represent the isospectral case,
i.e.,
a(Hm,*)
=
Wo),
(4.41)
where
(4.42)
d2
Hm,*
=
--
dx2
+
Vm,f,
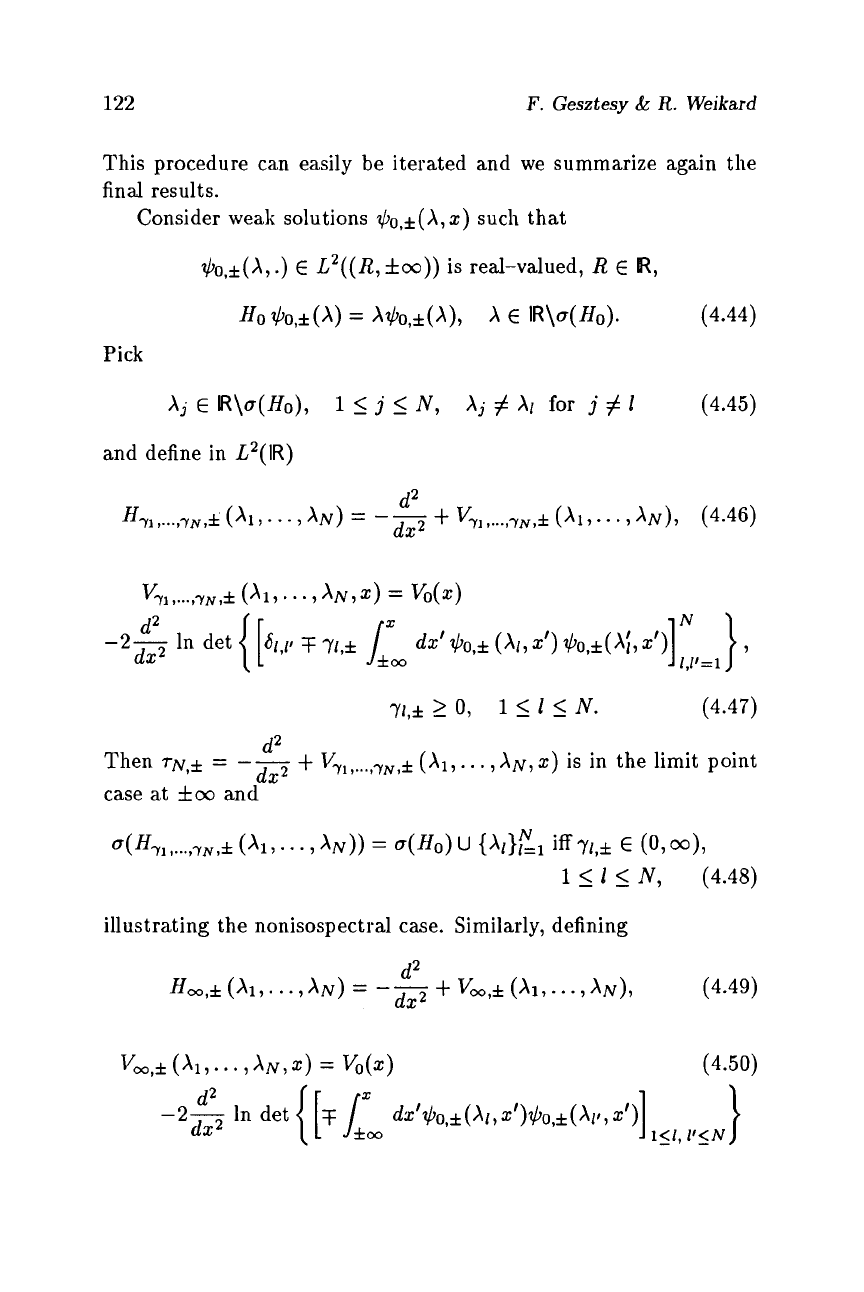
122
F.
Gesztesy
&
R.
Weikard
This procedure can easily be iterated and we summarize again the
final results.
Consider weal; solutions
$o,*(X,
x)
such that
Xj
E
IR\a(Ho),
1
5
j
5
N,
Xj
#
XI
for
j
#
1
(4.45)
and define in
L2(
IR)
71,k
2
0,
1
5
1
5
N.
(4.47)
y1
,...,
yr,f
(XI,..
.
,
AN,
x)
is in the limit point
Then
TN,~
=
--
+
V
case
at
foo
and
d2
dx2
illustrating the nonisospectral case. Similarly, defining

Spectral Deformations and Soliton Equations
123
yields the isospectral counterpart, i.e.,
(actually, one can show that
H,,i(X1,.
. .
,A,)
and
Ho
are unitarily
equivalent
[25]).
In the particular case where
VO
is the finite-gap potential
(4.27),
equation
(4.50)
becomes
In
n
Voo,i(X1,**.,XN,x)
=
C
Em
-2C
Xj
(4.52)
m=O
j=1
QI
=
(XI,-
Ii2n+1(~1
t
,
1
I
1
5
N.
A
comparison of
(4.52)
and
(4.28)
reveals that in the finite-gap
context one double commutation at
X1
corresponds to two single
commutations at
A1
and
X2
in the limit
X2
+
XI.
Actually this fact
is independent of the finite-gap context and holds in general. Indeed,
taking into account the identity
dx’
+O,&(Al
,
X/)$O,i(X2,X/>
(4.53)
=
(A1
-
x21-l W+O,&(Xl), +O,i(X2))(2>,
X1,
A2
E
IR\a(ffo),
A1
#
A2
L
and the fact that
lV(+o,+(Xl), &,-(XI))
is
a
nonzero constant, one
infers, e.g.,
(4.54)
€1
=
-€2
XzfXl
{
7::l)iAl,2),
€1
=
€2.
Finally, with
a
slight adjustment only, one can also use directly
formulas
(4.39)
resp.
(4.47)
to produce potentials isospectral to
VO.

124
F.
Gesztesy
&
R.
Weikard
E.g., if
A1
is already an eigenvalue of
Ho,
A1
E
a,(Ho)
(4.55)
then
Ifrl,*
in
(??)
and
(??),
with
$o,+(Xl,z)
=
c$o,-(A~,z)
the
corresponding eigenfunction of
Ho,
are well defined. In this case
one only changes the corresponding norming constant of the eigen-
function of
Hrl,* associated with
A1
and hence
ITrl,*
and
Ho
are
isospectral
Wr1,*)
=
Wo).
(4.56)
(A
further extension, allowing
=
-
I[$o,*(A1)11~,
removes the
eigenvalue
A1
from
110,
i.e.,
a(Hrl,*)
=
a(Ho)\{A}
in this case.)
These facts are illustrated, e.g., in
[l],
[58].
It should perhaps be pointed out again at this occasion that the
substitution
$o,i(
Aj
3
z)
-
$o,*
(Aj
9
2,
t
)
(4.57)
in
(??),
(??),
(??),
where
+o,*(Aj,z,t)
satisfies
HO
$o,&(Aj)
=
Aj
$o,?~(~j)7
at
+o,*(Aj)
=
P2n+1
$o,k(Aj),
1
I
j
I
N
(4.58)
and
Vo
satisfies the n-th KdV equation
lidVn(Vo)
=
0,
(4.59)
Vr1
....,
9
?N,f
(A1
,...,
AN,
2,
t),
voo*
(A1
,...,
AN,
2,
t)
ofthe n-th KdV equa-
produces again solutions
V(A1,
€1,.
.
.
,
AN,CN,
z,t)
and
tion.
5
Isospectral Sets
of
Quasi-Periodic
Finite-Gap Potentials
In this section we fix
a
real-valued quasi-periodic finite-gap potential
Vi(z)
satisfying Hypotheses (H.3.1) and (H.3.2) and
n
in+l,z(vO)
=
C
cn-j
fj+l,z
(1’0)
=
0
(54
j=O
for some fixed
{cj}Y=o
c
IR,
co
=
1

Spectral Deformations
and
Soliton Equations
125
with the associated noiisingular compact hyperelliptic curve
Kn
=
Icn
(
VO
)
(cf.
(2.23), (2.26),
and
(2.27)).
Thus
VO
can be represented by the
Its-Matveev formula
(4.27)
2n
n
VO(Z)
=
c
Em
-2c
xj
m=O
j=1
The isospectral set
IIR(
I+,)
of
real-valued quasi-periodic finite-gap
potentials of
VO
is then defined by
I~(v0)
=
{V
E
Cm(IR),
real-valued
fn+1,i(V)
=
0,
I*
I<n(V)
=
Iin(Vo)},
(5.4)
where
fn+l,,
is given in terms
of
the sequence
{~j}j”,~,
co
=
1
in
(5.1)
and
Iin(V)
=
I<,(Vo)
denotes the fixed hyperelliptic curve
(5.2).
In order to give an explicit realization of
I~(v0)
we need to in-
troduce the following sets
DR*
c
on
I<,,
of positive divisors in “real
position” (see Section
3
for the terminology employed)
where
K
denotes some permutation of
{
1,.
. .
,
n}.
The Its-Matveev formula
(3.36)
and the fact that Dirichlet divi-
sors
D;,(,)+...+8n(r)
are nonspecial then yields the following theorem
(see, e.g.,
[4], [51, [IT], [211,
WI,
[441, [48l, [5Ol, [571).

126
F.
Gesztesy
&
R.
Weikard
Theorem
5.1
The map
is bijective, where
2n
n
m=O
j=1
and the associated Dirichlet divisor
Dbl
(t)+...+fin(l)
is
obtained from
(3.40)
by
solving the system
(2.29)
with initial conditions
(3.41).
Next we state the following "real" version
of
the Jacobi inversion
theorem
(3.33).
Lemma
5.2
Denote
by
[4]
the equivalence class
ofg
€an
in
J(Kn)
=
an/L,.
Then
Sketch
of
proof.
Due to the fact that
I[i2n+l(t)1/2
is real-valued
iff
z
E
U
ijj
and
n
j=O
one can show t1ia.t
(5.10)

Spectral Deformations and Soliton Equations
127
(5.9)
then follows from
(3.33)
by restricting
'ypm
to
DR
-
.
Next we introduce the notion of admissibility
of
divisors:
a
pos-
itive divisor
Dpl
+
e
-
+
Pn
E
onKn
is called admissible iff there is
no pair
(P,P*)
E
{PI,
...,
Pn}
with
P
E
lin\{P,}.
The set of
all
admissible divisors is denoted by
A.
We note that admissible divisors
Dp,+...+p,
E
A
are either non-
special
or
their speciality stems from one
or
more points P, con-
tained in
{&,
.
.
.
,
P,}.
Lemma
5.3
Given
Dfi~+...+fi~
E
DR,
and
Dcl+
...+I;,
E
DR,
there
exists
Q
unique divisor
~Q~+...+Q,,
E
DR
-
fl
A
such that
gPm
(Dfi1+...+fin)
=
EPm
('by+
...+fi
0,)
-
EPm
(DQI+...+Qn).
(5.12)
n
j=1
Sketch
of
proof.
Since i2n+l(t)1/2 is real-valued
if
z
E
U
pj,
(5.12)
is equivalent to
n
'YP-
(DQ~+...+Q~)
=
-
C
~fiy
(Lr(j))
E
{[:I
E
J(I{~)
I
z
E
IRn
}
j=l
(5.13)
for some permutation
A
of
(1,.
.
.
,
n}.
Thus the existence of some
DQ~+
...+Q,
E
DIR
-
satisfying
(5.12)
follows from Lemma
5.2.
If
DQ]+
...+Q,
is nonspecial then
DQ]+
...+Q~
E
A
is clearly the unique
solution of
(5.12).
If on the other hand
n
2
2
and
{QI,
...
,Qn}
contains
a
pair
(P,
P*)
with
II(P)
E
(-00,
Eo], say Q1
=
P,
Q2
=
P*,
then simply replace Q1 and Q2 by
P,
since
'Ql+Qz+Q3+..*+Qn 'f'-+pm+Q3+.*.+Qn
(5.14)
by Abel's theorem
(3.32).
By continuing this process of replacing
pairs
(P, P*), P
#
P, by
(P,,
P,) one finally ends up with
a
unique
admissible divisor linearly equivalent to the original
DQ]+
...+Q,.
Our new main result on
I~(lf0)
then reads
Theorem
5.4
[27]
The
n1a.p
(5.15)

128
F.
Gesztesy
&
R.
Weikard
is bijective, where
DQ~+
...+Q~
E
VR-
n
A
is the unique solution
of
h!foTeoveT,
2n
n
=
c
Em-2CXj
m=O
j=1
where
Sketch of proof.
Existence and uniqueness
of
DQ~+
...+Q,,
E
DR-
n
A
in (5.15) associated with
Vfilr...,fin
by
(5.16) follows from Lemma
5.3. (5.17) and (5.18) are
a
consequence of
(4.24)
and
(4.28).
Remark
5.5
An explicit realization of
I*(Vo)
in the case where
VO
is
a
real-valued periodic finite-gap potential has first been derived
by
Finkel, Isaacson, and Trubowitz [21]. We also refer to [9], [35], [37],
[51]-[53], [59], and
[G2]
for
further investigations in this direction.

Spectral Deformations and Soliton Equations
129
Our
realization
(5.17)
of
I~(v0)
differs from the one in
[21]
in two
respects. First of all, for fixed genus
n,
(5.17)
involves at most an
n
x
n
Wronskian as opposed to
a
2n
x
2n
Wronskian in
[all
(involving
n
additional Dirichlet eigenfunctions) and secondly,
(5.17)
does not
assume periodicity but applies to the quasi-periodic finite-gap case.
The upshot of
(5.17)
is the following: the entire isospectral torus
I~(v0)
of the given base potential
Vo
is generated by
at
most n-single
commutations associated with
(XI,
€1,.
.
.
,A,,
en),
where the points
Qj
=
(Aj,-~jI&~+l
(Xj
+
iO)li21),
1
5
j
5
n
vary independently of
each other on both rims of the cut
Po
=
[-00,Eo]
(avoiding pairs
of
the type (QYQ'),
Q
#
f'co
in {Q1,.-.,Qn)).
One can prove an analogous representation for
I~(v0)
by using
the isospectral double commutation a.pproach
(4.49)-(4.52) [27].
6
Some Generalizations
In our final section we comment
on
some
natural generalizations of
the approach in Sections
4
and
5
and mention some open problems.
a)
The case where
Vo
E
(I"(IR)
is real-valued and periodic of period
a
>
0
with infinitely many spectral gaps in
a(H0)
is well understood
Infiiiitely Many Spectral Gaps in
c(W,,):
WI,
WI,
[371,
WI,
P71, [541, P51, [591,
If
~(110)
=
IJ
[~2(j-1),
~2j-11,
(6.1)
jclN
then
Vo
can be approximated uniformly on
IR
by
a
sequence of real-
valued finite-gap potentials
T~o,~
(of the same period
u)
associated
with
K,
in
(5.2)
as
n
-+
00.
In
this context determinants of the type
(4.24)
and
(4.50)
converge to Fredholm determinants as
n
+
00
(we
shall illustrate this in some detail in
a
similar context
at
the end of
this section).
These results have been extended to particular classes
of
real-
valued almost periodic potentials
VO
E
P(R)
with suitable condi-
tions on the asymptotic behavior of
Ej
as
j
-+
00
in
[lo],
[39]-[44].
