Ames W.F., Harrel E.M., Herod J.V. (editors). Differential Equations with Applications to Mathematical Physics
Подождите немного. Документ загружается.


90
D.
Fusco
and
N.
Manganaro
2
The
Governing
Model and
Similarity
Reduct
ion
Flows in fluid-filled elastic tubes can be described by the following
system of equations
[13]
S
vsx
+
Q
SP
SP
Pt
+
vpx
+
-
v,
=
-
vt
+
kpx
+
VVX
=
f
-
kPx
(2.2)
where
p
is the transmural pressure,
v
is
the fluid velocity,
S
=
S(p,
x)
is the cross-sectional area and it is assumed
S/S,
>
0,
P
=
P(z,t)
is the external pressure,
k
=
l/p
with
p
being (constant) density,
Q
=
Q(p,
v,
z)
represents the outflow function and
f
=
f
(p,
v, x,
t)
is
the viscous retarding force.
S,
Q
and
f
are the concerned material
response functions which have to be specified in the present case. In
general they depend upon the field variables
p
and
v
as
well
as
upon
the independent variables
x
and/or
t
so
that the governing model
(2.1), (2.2)
results to be nonautonomous.
In
[14]
there has been shown that the system of equations un-
der interest
is
invariant with respect to infinitesimal transformation
groups if the involved response functions obey the restrictions
f
=k(ap+b)+
:v2+kPx+H(II,w)exp
(/+)
(2.5)
where
l-I
=
(P-Po)exP
(-
J
a(z)dx)
-1
b(z)
exp
(-
/
a(x)dz) dx
(2.6)
w
=
vexp (-/idx)
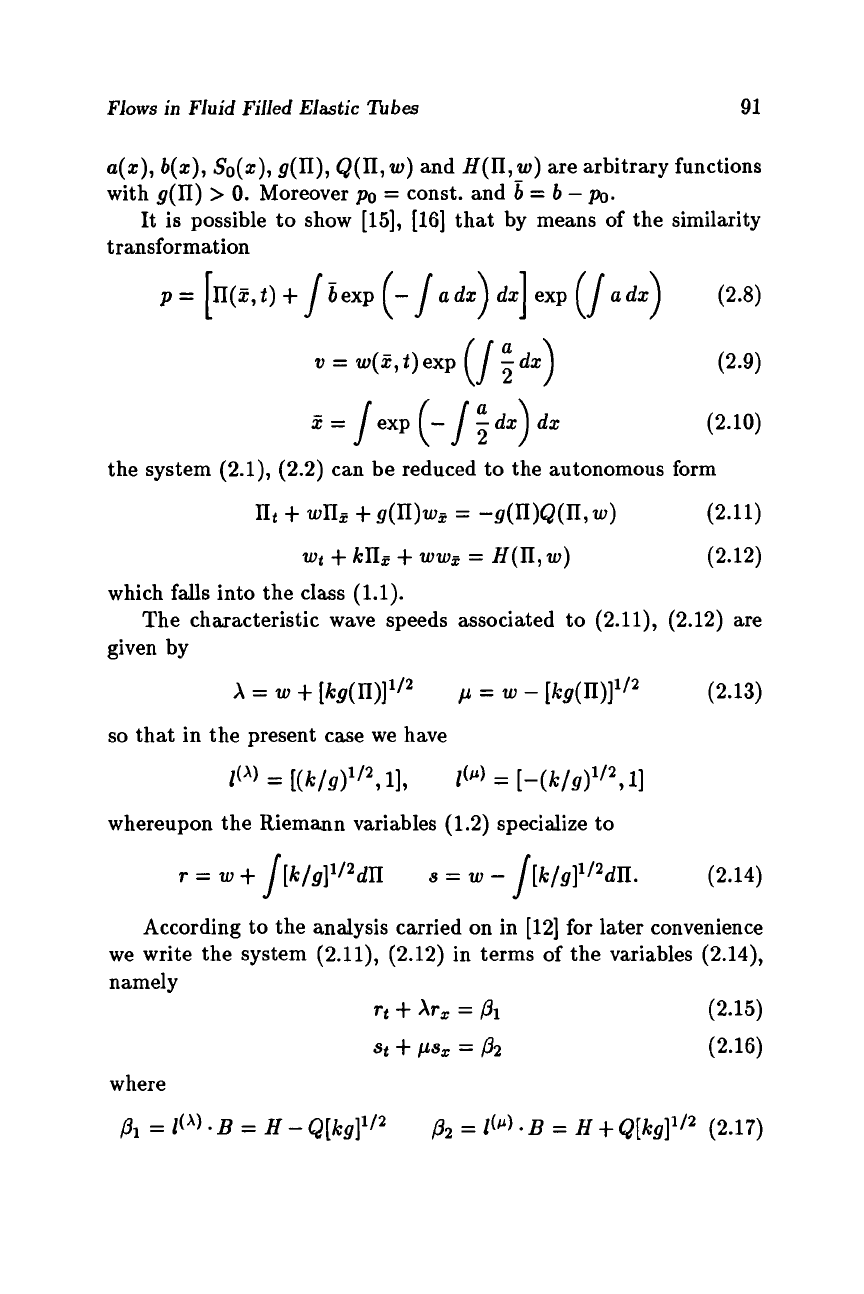
Flows
in
Fluid Filled Elastic
nbes
91
a(x),
b(z),
So(z),
g(II),
Q(II,
w)
and
H(II,
w)
are arbitrary functions
with
g(II)
>
0.
Moreover
po
=
const. and
6
=
b
-
po.
It is possible to show
[15], [16]
that by means of the similarity
transformation
p=
[n(z,t)+/6exp(-/odx)dx]
exp(/adx)
(2.8)
v
=
w(3,
t)
exp
(1
;
dx)
5
=
/exp
(-/:dx) dx (2.10)
the system
(2.1), (2.2)
can be reduced to the autonomous form
nt
+
wnz
+
g(n)wz
=
-g(n)Q(n,
w)
wt
+
kIIz
+
wwz
=
H(II,w)
(2.11)
(2.12)
which falls into the class
(1.1).
given by
The characteristic wave speeds associated to
(2.11), (2.12)
are
x
=
w
+
[kg(II)]'/2
/I
=
w
-
[kg(II)]1/2
(2.13)
so
that in the present case we have
P)
=
[(k/g)l/2,1],
I(@)
=
[-(k/g)1/2,1]
whereupon the Riemann variables
(1.2)
specialize to
T
=
20
+
/[k/g]1/2dII
s
=
w
-
/[k/g1112dn.
(2.14)
According to the analysis carried on in
[12]
for later convenience
we write the system
(2.11), (2.12)
in terms of the variables
(2.14),
namely
rt
+
xr,
=
PI
(2.15)
St
+
/Is2
=
P2
(2.16)
where

92
D.
Fusco and
N.
Manganaro
3
Existence
of
Riemann-Like Invariant
Quantities and Exact Solutions
It is
well
known that if the wave speeds
A
and
p
satisfy the excep-
tionality conditions
[3]
VA
*
&)
=
0
vp
*
d(P)
=
0
(3.1)
where
V
=
z,
then
T
=
p
and
s
=
A.
Consequently, for
2
x
2
homogeneous hyperbolic and completely exceptional (CEX) systems
the Riemann invariants are given by the characteristic speeds.
A
classical example is given by the system of isentropic fluid-dynamics
supplemented by
a
V6n-Karman-like
p
-
p
law.
Bearing in mind
(2.15)
and
(2.16)
the aforementioned result con-
cerning Riemann invariants is no longer true for
2
x
2
nonhomoge-
neous CEX systems (otherwise it turns out to be
B
=
0).
Within the
theoretical framework outlined in the introduction let us require the
system
(2.15), (2.16)
to be consistent with two additional equations
of the form
(1.3)
and
(1.4)
where
F
=
p
and
G
=
A,
respectively,
so
that
(1.5)
is fulfilled.
Of
course, taking into account the remark
made above about nonhomogeneous
2
x
2
systems, we assume that
the characteristic wave speeds do not satisfy the exceptionality con-
ditions
(3.1).
Looking for solutions
of
(2.11), (2.12)
(or
equivalently of
(2.15),
(2.16))
such that
#
#
0
and owing to
(1.5)
we can perform the
following change
of
variables
(a a)
Z
=
2(F,G)
=
ii(A,p)
t
=
t(F,G)
=
t(A,p)
(3.2)
whereupon the set
of
equations
(2.11), (2.12), (1.3), (1.4)
takes the
form
(3.3)
P1
=
-
zx
=
Xtx
i3P
=
pt,
(3.4)
TA
5P
P2
=
-
tx
t
P
Cross differentiation in
(3.4)
produces the wavelike equation
tx,
=
0
(3.5)
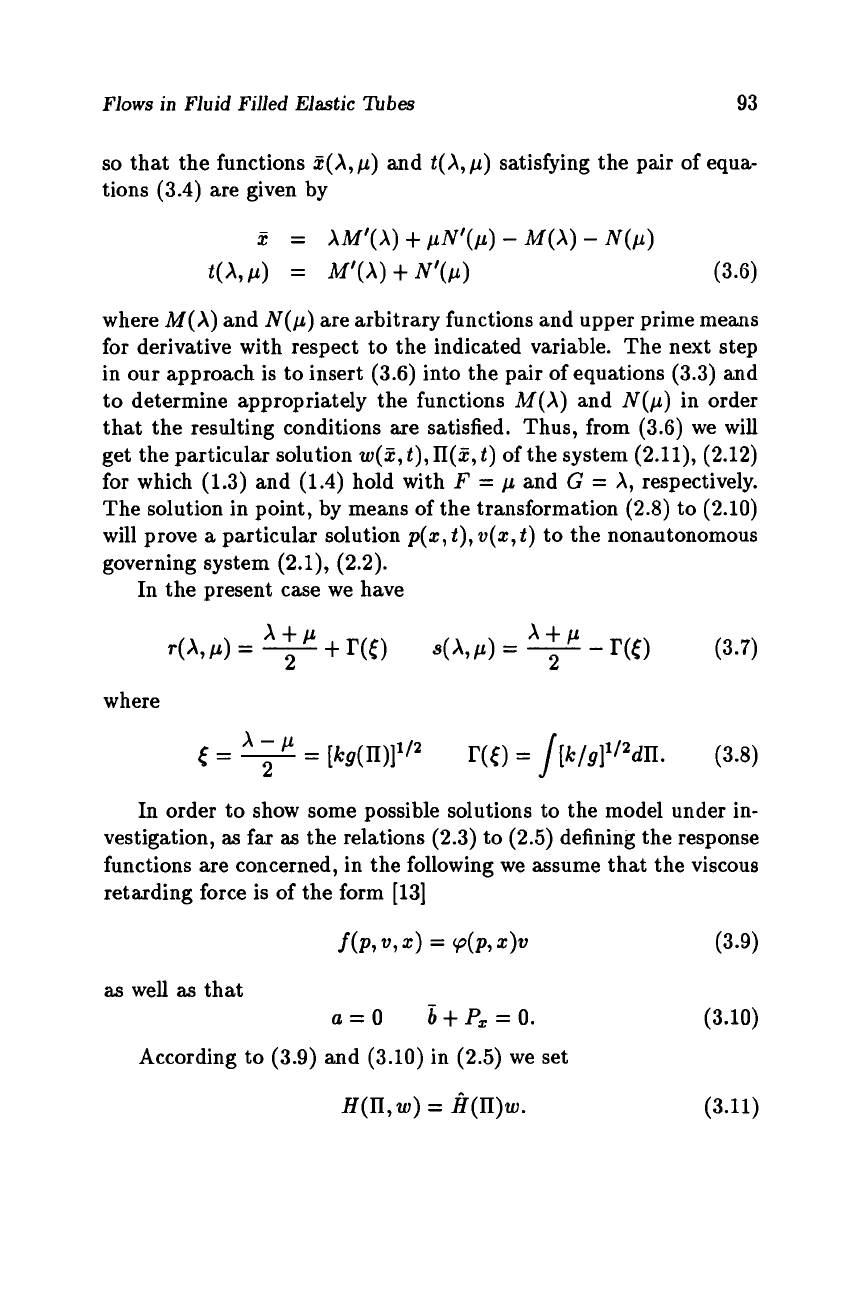
Flows
in
Fluid Filled Elastic
nbes
93
so
that the functions
i?(X,p)
and
t(X,p)
satisfying the pair of equa-
tions
(3.4)
are given by
where
M(X)
and
N(p)
are arbitrary functions and upper prime means
for
derivative with respect to the indicated variable. The next step
in our approach is to insert
(3.6)
into the pair of equations
(3.3)
and
to determine appropriately the functions
M(X)
and
N(p)
in order
that the resulting conditions
are
satisfied. Thus, from
(3.6)
we will
get the particular solution
w(i?,t),
n(i?,t)
of the system
(2.11), (2.12)
for which
(1.3)
and
(1.4)
hold with
F
=
p and
G
=
A,
respectively.
The solution in point, by means of the transformation
(2.8)
to
(2.10)
will prove
a
particular solution
p(z,
t),
v(z,
t)
to the nonautonomous
governing system
(2.l), (2.2).
In the present case we have
where
In
order to show some possible solutions to the model under in-
vestigation,
as
far
as
the relations
(2.3)
to
(2.5)
defining the response
functions are concerned, in the following we assume that the viscous
retarding force is
of
the form
[13]
as
well
as
that
a=O
5+Pz=0.
(3.10)
According to
(3.9)
and
(3.10)
in
(2.5)
we set
H(ll,w)
=
@(n)w.
(3.11)

94
D.
Fusco
and
N.
Manganaro
Relations
(2.17)
yield
Q
=
&@
and
H
=
9
so
that owing
to
(3.6), (3.7)
the pair of equations
(3.3)
specializes to
(3.12)
(3.13)
where
m(X)
=
MTJ
1
and
n(p)
=
A
direct inspection shows that the system of equations
(3.12),
(3.13)
are satisfied if
M(X)
and
N(p)
fulfill the relations
m(X)
=
mo
+
mlX
+
m2X2
n(p)
=
-mo
+
mlp
-
m2p2 (3.14)
where
mo,ml,m2
are constant and in turn the functions
Q
and
fi
involved there adopt the form
(3.16)
with g(n) arbitrary. In deducing
(3.15)
and
(3.16)
use has been made
of relations
(3.8).
By prescribing
g(II),
i.e., through
(2.3)
the cross-sectional area
law, the insertion of
(3.15)
and
(3.16)
into
(2.4)
and
(2.5)
will define
possible model laws for the outflow functions and for the viscous
force
f
(linearly dependent upon velocity according to
(3.9)).
In particular by assuming
(3.17)
n
=
with
h
#
0
constant,
(2.3)
specializes to
(3.18)

Flows
in Fluid Filled
Elastic
nbes
95
with
SO(X)
and
IIo
=
const. arbitrary, whereas (2.4) and (2.5),
re-
spectively, reduce to
dx
}
+
(f
+
h)
(t
)
112
(p
-
po
+
P)+
1
x
[
(t>
(p
-
Po
+
P)l12
+
1
t
m2v2)
1/2
(3.19)
f(p,
0,
x)
=
(f
+
h)
{m,
+
2mz(Ln0/h)'/~(S/So)'IZh)
v.
(3.20)
Within the present framework
as
far
as
the exact solutions to
system of equations (2.11), (2.12) are concerned, from (3.6) several
possibilites arise in connection with different choices
of
the parame-
ters
mo,
ml
and m2 involved
in
relations (3.14)
as
well
as
in (3.19)
and
(3.20).
Here we will consider only two cases where explicit solu-
tions to the system under investigation can
be
obtained.
i)
mo
=
0, ml
#
0
and m2 arbitrary. By inverting (3.6) and
making use
of
the variable transformation (2.8) to (2.10) we gain
where
x=x+M
r=t-N
(3.23)
and
i$f
and
fi
are arbitrary constants coming out from integrating
(3.14).

96
D.
Fusco
and
N.
Manganaro
ii)
mo
=
0,ml
=
O,m2
arbitrary. Here an approach similar to
that above yields
emZx
-
e-mZX
v(x,t)
=
2m2r
(3.25)
In
both cases i) and ii) considered above there are no restrictions
on the function
P(x)
simulating external pressure in the governing
model
(2.11), (2.12).
4
Conclusions and Final Remarks
The method of approach we developed herein in order to determine
exact solutions to the nonautonomous system governing flows in
fluid-filled elastic tubes was essentially based on two steps. First, by
considering the general classes of material response functions
(2.3)
to
(2.5)
allowing for the existence of group symmetries to the model
in point as shown in
[14],
we used the similarity-like variable trans-
formation
(2.8)
to
(2.10)
in order to reduce the system of equations
(2.1), (2.2)
to the autonomous form
(2.11), (2.12).
Furthermore for
the latter system we worked out
a
procedure for finding out the con-
cerned solutions for which the model
(2.11), (2.12)
is consistent with
two additional equations like
(1.3)
and
(1.4)
with
a
prescribed form
of
F
and
G
suggested by
a
well established result for
2
x
2
quasilinear
homogeneous hyperbolic systems of first order.
Of
course, along the
same lines of the analysis worked out hitherto other forms of
F
and
G
can be considered. In these cases
a
leading idea to prescribe
F
and
G
is to achieve, by means of the transformation
(3.2),
a
hodograph-like
system (see
(3.4))
which can be reduced to
a
canonical form dowing
for an explicit integration
[4], [5].
In the process we have been able to
provide
a
vehicle for characterizing possible model constitutive laws
to the governing system under interest. About that concern we re-
mark that we have some freedom to choose the function
g(n)
which
characterizes the cross-sectional area law and which is involved also

Flows
in Fluid Filled Elastic
’Ibbes
97
in
(3.15)
and
(3.16).
Finally, we showed some (explicit) exact solu-
tions to
(2.1), (2.2)
which can be obtained by means of the present
method of approach. Nevertheless, the relations
(3.6)
with
M(X)
and
N(p)
defined by
(3.12)
may provide further exact solutions
to
the model in point although they will be determined in general in an
implicit way. Apart their own theoretical value these solutions can
be used for testing numerical procedures to the system
(2.1), (2.2)
as
well as for studying wave propagation into nonconstant states repre-
senting nonuniform tube flow regimes where dissipation is taken into
account.
This work was partially .supported by
M.U.R.S.T. through “Fondi per
la
Ricerca Scientifica
40%
and
60%”
and by C.N.R. through G.N.F.M.
Acknowledgements.
Bibliography
[l]
C. Rogers and
W.
F.
Ames,
Nonlinear Boundary Value Prob-
lems in Science and in Engineering,
Academic Press, New York
(1989).
[2]
C. Rogers and
W.
F.
Ames,
Nonlinear Equations in Applied
Sciences,
Academic Press, New York
(1992).
[3]
A. Jeffrey,
Quasilinear Hyperbolic Systems and Waves,
Pitman,
London
(1976).
[4]
C.
Currb and
D.
Fusco,
Reduction to linear canonical
forms
and genemtion
of
conservation laws
for
a class
of
quasilinear
hyperbolic systems,
Int.
J.
Non-Linear Mech.
23, 25-35 (1988).
[5]
C. Currb and
D.
Fusco,
On
a class
of
quasilinear hyperbolic
re-
ducible systems allowing
for
special wave interactions,
Z.
Angew.
Math. Phys.
38, 580-594 (1987).
[6]
B.
Seymour and
E.
Varley,
Ezact solutions describing soliton-
like intemctions in a nondispersive medium,
(SIAM)
J.
Appl.
Math.
42, 804-821 (1982).

98
D.
Fusco
and
N.
Manganaro
[7]
B.
Seymour and
E.
Varley,
Exact solutions for large amplitude
waves in dispersive and dissipative systems,
Stud. Appl. Math.
72, 241-262 (1985).
[8]
D. Fusco and
N.
Manganaro,
Linearization of
a
hyperbolic
model for non-linear heat conduction through hodograph-like
and Bicklund transformations,
Int.
J.
Non-Linear Mech.
24 (2),
99-103 (1989).
[9]
D. Fusco and
N.
Manganaro,
Prominent features of
a
variable
tmnsformation for
a
class of quasilinear hyperbolic systems of
first order,
Nonlinear Wave Motion, edited by A. Jeffrey, Long-
man,
71-82 (1989).
[lo]
D. F’usco and
N.
Manganaro,
Recent contributions to wave prop-
agation
in
nonlinear dissipative media,
Numerical and Applied
Mathematics, edited by W.
F.
Ames, Baltzer Scientific Publish-
ing,
101-105 (1989).
[ll]
D. Fusco and
N.
Manganaro,
A
class of linearizable models and
generation of material response functions to nonlinear hyperbolic
heat conduction,
J.
Math. Phys.
32, 3043-3046 (1991).
[12]
D. F’usco and
N.
Manganaro,
Generation of exact solutions to a
class
of
quasilinear hyperbolic models via reduction techniques,
to appear.
[13]
T.
J.
Pedley,
The Fluid Mechanics of Large Blood Vessels,
Cam-
bridge University Press, Cambridge
(1980).
[14]
D. Fusco,
Group analysis and constitutive laws for fluid filled
elastic tubes,
Int.
J.
Non-Linear Mech.
19 (6), 565-574 (1984).
[15]
N.
Manganaro,
Linearization of non autonomous models de-
scribing fluid-filled elastic tubes and nonlinear elastic
rods
with
variable cmss section,
in print on Acta Mechanica.
[16]
A. Donato and
F.
Oliveri,
When non autonomous equations
are
equivalent to autonomous ones,
to
appear.

Flows
in
Fluid Filled Elastic
nbes
99
[17]
G.
Boillat
and
T.
Ruggeri,
Characteristic
shocks:
completely
and strictly exceptional systems,
Boll.
U.M.I.
5 (15-A), 197-204
(1978).
