Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics

Подождите немного. Документ загружается.

This page intentionally left blank

Sunden CH006.tex 10/9/2010 15: 39 Page 217

6 Time-accurate techniques for turbulent heat

transfer analysis in complex geometries

Danesh K. Tafti

Department of Mechanical Engineering, Virginia Polytechnic

Institute and State University, VA, USA

Abstract

With the large increase in computational power over the past two decades, time-

dependent techniques in turbulent heat transfer are becoming more attractive and

feasible.Thechapter describes the numericaland theoretical background to enable

the use of these methods in complex geometries.

Keywords: Heat exchangers, Large-eddy simulations (LES), Parallel computing,

Turbomachinery, Unsteady CFD

6.1 Introduction

Heattransferdevicesspanawiderangeofapplicationsintheautomotive,aerospace,

electronics, powergeneration, and biomedical industries with characteristiclength

scales ranging from a few hundred microns to meters. The characteristic Reynolds

numbers (Re) can range from low and largely viscous (Re< 10) to high and fully

turbulent(Re> 2,000).Whilepredictionsin thelaminar regime donot posesignif-

icantcomputationalchallenges, barringstrongpropertyvariations,non-Newtonian

ﬂows, or signiﬁcant body forces, predictions in the transitional and turbulent

regime pose considerable challenges. In these ﬂow regimes common techniques

employed are direct numerical simulations (DNS), large-eddy simulations (LES),

Reynolds-averagedNavier–Stokes(RANS)orunsteady RANS(URANS).DNSby

deﬁnition requires that the full spectrum of turbulence down to the smallest dis-

sipative scales be resolved in the calculation. As the Reynolds number increases

beyond O(10

−10

) in wall-bounded ﬂows, resolving the full spectrum becomes

exceedingly expensive, which limits the application ofDNS. LES extendsitsprac-

tical range to Reynolds number of O(10

−10

) by resolving scales only up to the

inertial range and modeling the smaller scales via a subgrid stress model. RANS

extendsthisrangefurthertoveryhighReynoldsnumbersbymodelingthefullspec-

trum of turbulent scalesand incorporating theirtime-averaged effectinto the mean

Sunden CH006.tex 10/9/2010 15: 39 Page 218

218 Computational Fluid Dynamics and Heat Transfer

momentum and energy balance. URANS is used in cases where external forcing

is present at a given frequency or the ﬂow has an intrinsic characteristic frequency

(as in shedding of large-scale structures). By resolving only the large-scale time-

dependent structures and modeling the smaller-scale turbulence, the required grid

density is still much less than other time-dependent methods.

ThehighcomputationalcostofDNSandLESontheonehandandtheprediction

uncertainty of RANS on the other has led to the development and application of

hybrid RANS-LES methods, which have tried to combine the low cost of RANS

withthesuperioraccuracyofLES.Outofthisfamilyofhybridtechniques,detached

Eddysimulation(DES)hasgainedpopularitysinceitwasproposedbySpalartetal.

[1] in 1997 for external ﬂows with massive separation. DES involves sensitization

of aRANSmodel to grid length scales, thereby allowing it tofunction as a subgrid

stress model in critical regions.

Alltheabovemethodsarevalidintherangeofﬂowsencounteredinheattransfer

devices.For example, RANS and URANSand maybeDES are more readily appli-

cableto system-levelsimulations, whereas DNS and LES aremoreappropriate for

component-level simulations.

Thechapter focusesonthe applicationofthese techniquestocomplexturbulent

ﬂows highlighting the related theoretical and computational background from the

author’s research experience. It starts with the transformed conservation equations

in general coordinate systems and their solution in a multiblock computational

framework.The nonstaggeredgridpressureequation isrelated toits staggeredgrid

counterpart giving perspective to different approximations used in the literature

and the formulation ﬁnally used. A section is also devoted to the discretization

of the convection term and its effect on solution accuracy. This is followed by a

section on subgrid modeling in LES and the DES method. Finally, the solution of

linear systems and parallelization strategies on modern computer architectures are

discussed. The chapter is closed by referring to some recent application of these

techniques to complex heat transfer problems.

6.2 General Form of Conservative Equations

The continuum conservation of mass, momentum, and energy and the ideal gas

equation of state are described by the following time-dependent, conservation

equations (the superscript * is used to denote dimensional variables throughout

this chapter):

Mass conservation:

∂ρ

∗

∂t

∗



∇·(ρ

∗

u

∗

) = 0 (1)

Momentum conservation:

∂(ρ

∗

u

∗

)

∂t

∗



∇·(ρ

∗

u

∗

u

∗

) =−



∇P

∗



∇·

⎛

⎜

⎝

∗

(



∇u

∗



∇u

∗T

)

−

∗

(



∇·u

∗

⎞

⎟

⎠

+ ρ

∗

g

∗

(2)

Sunden CH006.tex 10/9/2010 15: 39 Page 219

Time-accurate techniques for turbulent heat transfer analysis 219

Energy conservation:

∂(ρ

∗

)

∂t

∗



∇·(ρ

∗

u

∗

) =



∇·(κ

∗



∇T

∗

) +



∂P

∗

∂t

∗

+u

∗



∇P

∗



+

∗

+ ρ

∗

g

∗

·u

∗

(3)

where



∗



∗

(



∇u

∗



∇u

∗T

) −

∗

(



∇·u

∗





∇u

∗

is the viscous-dissipation term.

Equation of state:

∗

(4)

Targeting applications in free and forced convection with variable ﬂuid prop-

erties, the equations are cast in nondimensional form by using the following

parametrization:

ρ =

∗

ref

µ =

∗

ref

κ =

∗

ref

∗

p_ref

x =

x

∗

ref

u =

u

∗

ref

t =

∗

ref

∗

ref

P =

∗

− P

∗

ref

∗

ref

∗2

ref

T =

∗

− T

∗

ref

∗

Thereferencetemperature,T

∗

ref

andpressureP

∗

ref

areusedforcalculatingallref-

erence property values, whereas T

∗

is the nondimensionalizing temperature scale.

The dynamic viscosity µ

∗

/µ

∗

ref

and thermal conductivity κ

∗

/κ

∗

ref

variations with

temperature are represented by Sutherland’s law for gases (White [2]).While these

twoquantities varysubstantiallywithtemperature, speciﬁcheat hasamuch weaker

dependence. For example, viscosity and conductivity for air in the temperature

range240to960Kvarybymorethan100%,whereasc

∗

onlyvariesby12%.Hence,

assuming that c

∗

p_ref

=1, and that g

∗

e

, the nondimensional equations are

written as:

Mass conservation:

∂ρ

∂t



∇·(ρu) = 0 (5)

Momentum conservation:

∂(ρu)

∂t



∇·(ρuu) =−



∇P +



∇·(µ(



∇u +



∇u

) −

µ(



∇·u)I)

(T)

e

(6)

Sunden CH006.tex 10/9/2010 15: 39 Page 220

220 Computational Fluid Dynamics and Heat Transfer

Energy conservation:

∂(ρT)

∂t



∇·(ρuT) =

RePr



∇·(κ



∇T) +Ec



∂P

∂t

+u ·



∇P









ρ e

·u

(7)

Equation of state:

ρ =

∗

ref

∗2

ref

P + P

∗

ref

∗

ref

(T · T

∗

+ T

∗

ref

)

(8)

where T in equation (6) is the characteristic nondimensional temperature

difference that drives the buoyant ﬂow,

Re =

∗

ref

∗

ref

∗

ref

∗

ref

,Pr=

∗

ref

∗

p_ref

∗

ref

,Ra=

∗

(T

∗

∗3

ref

∗

ref

∗

ref

Ec =

∗2

ref

∗

p_ref

∗

, and Fr =

∗2

ref

∗

ref

specify the Reynolds, Prandtl, Rayleigh, Eckert, and Froude number, respectively,

and β

∗

is the thermal expansion coefﬁcient.The reference velocity U

∗

ref

is selected

based on the dominating convection force. In forced convection, the reference

velocityis speciﬁed from the driving ﬂow, e.g., the free-stream velocity in external

ﬂow. In the case of pure natural convection, the reference velocity is calculated

from thecharacteristic length andthe drivingtemperature difference, as deﬁnedby

the following (dimensional) equation:

∗

ref



∗

ref

∗

T

∗

(9)

In equation (6), the nondimensional coefﬁcient of the gravitational body force

term, Ra/(Re

Pr), determines theg ravitationaleffecton theﬂowﬁeld. Inpure natu-

ral convection, the term takes on a value of unity after substitution of the reference

velocity (equation (9)), into the Reynolds number, whereas in forced convection,

when Re>> Ra, the coefﬁcient would be negligibly small. In mixed convection,

both the speciﬁed driving temperature difference and reference convective veloc-

ity determine the relative magnitude of the gravitational source term and hence of

natural versus forced convection.

6.2.1 Incompressible constant property assumption

Low-speed incompressible ﬂow with constant ﬂuid properties results in a number

of simpliﬁcations in the conservation equations. One of the main numerical con-

sequences of this assumption is the decoupling of density from pressure and the

Sunden CH006.tex 10/9/2010 15: 39 Page 221

Time-accurate techniques for turbulent heat transfer analysis 221

implicit assumption that pressure waves travel at inﬁnite speed relative to the ﬂow

velocities(Machnumber,Ma→0).TheEckertnumber,Ec=Ma

(γ −1)→0,and

the pressure work term in equation (7) makes a negligible contribution to energy

conservation and can be neglected. In addition it is also customary to neglect the

viscous dissipation term (Ec/Re→0) and the potential energy term (Ec/Fr→0).

However, it is notewor thy that for very low Reynolds number highly viscous ﬂow

conditions might exist at which the viscous dissipation term can no longer be

neglected.After simpliﬁcations, the nondimensional equations take the form:

ρ =

∗

ref

= 1; µ =

∗

ref

= 1; κ =

∗

ref

= 1; c

∗

p_ref

= 1

x =

x

∗

ref

; u =

u

∗

ref

; t =

∗

ref

∗

ref

; P =

∗

− P

∗

ref

∗

ref

∗2

ref

T =

∗

− T

∗

ref

∗

Mass conservation:

∇·u = 0 (10)

Momentum conservation:

∂u

∂t



∇·(uu) =−



∇P +



∇·





∇u



+ ge

(11)

Energy conservation:

∂T

∂t



∇·(uT) =



∇·



Re Pr



∇T



(12)

where g =1/Fr=g

∗

ref

∗2

ref

For small temperature and density differences ( ρ

∗

= ρ

∗

ref

+ ρ

∗

) with other

properties held constant, the Boussinesq approximation can be accommodated in

equation (11) by replacing the last term with ge

(1 −T)ifT

∗

ref

= T

∗

Fully developed assumption

Inanumberofapplicationsthegeometrylendsitselftoconsiderablecomputational

simpliﬁcation by consideringa singleperiod ofarepeating featurein spacesuch as

in an array of ﬁns and in ducts with repeating roughness elements.This is done by

invoking afully-developed assumption in the ﬂow direction, thus allowing simula-

tion of a characteristic unit of the ﬂow.This formulation was developed for steady

ﬂow by Patankar et al. [3] for both a constant heat ﬂux and a constant tempera-

ture boundary condition. Because ofthe usefulness of thisformulation for detailed

analysis of ﬂow physics and heat transfer with time-dependent techniques, it is

repeatedhereforaconstantheat ﬂuxboundary conditioninthecontextof unsteady

ﬂow and heat transfer under conditions of a ﬁxed pressure gradient and a develop-

ing ﬂow ﬁeld. Under these conditions, the wall friction velocity u

∗



∗

/ρ

∗

Sunden CH006.tex 10/9/2010 15: 39 Page 222

222 Computational Fluid Dynamics and Heat Transfer

used as thereference velocity to nondimensionalizethegoverning equations. For a

fully-developed ﬂow a mean momentum balance in the ﬂow direction (x) gives the

following relationship:

∗

ref

= u

∗



∗

/ρ

∗



(−P

∗

)(D

∗

/4ρ

∗

) (13)

where τ

∗

is an equivalent mean wall shear which also includes form losses in the

domain, P

∗

is the mean pressure drop in the ﬂow direction across the computa-

tional domain length of L

∗

, and D

∗

is the hydraulic diameter. The characteristic

temperature scale is deﬁned as T

∗

ref

/κ

∗

, where −q

∗

is the applied wall

heat ﬂux. Since both pressure and temperature have a x-directional dependence,

the assumed periodicity of the domain in the streamwise or x-direction requires

the mean gradient of pressure and temperature to be isolated from the ﬂuctuating

periodic components as follows:

∗

(x,t) = P

∗

ref

− β

∗

+ p

∗

(x,t)

∗

(x,t) = T

∗

ref

+ γ

∗

(t) ·x

∗

+ θ

∗

(x,t)

(14)

where β

∗

=−P

∗

is the mean pressure gradient, p

∗

is the periodic pressure

ﬂuctuations, γ

∗

is a time-dependent temperature gradient, and θ

∗

is the ﬂuctuating

or periodic temperature component. Nondimensionalizing equation (14) gives

P(x,t) =−βx + p(x,t)

T(x,t) = γ (t)x + θ (x,t)

(15)

where β =4/D

from equation (13).

Substituting equation (15) in the nondimensional conservation equations (10)–

(12) gives the following modiﬁed momentum and energy equations:

Momentum conservation:

∂u

∂t



∇·(uu) =−



∇p +



∇·





∇u



+ ge

+ βe

(16)

Energy conservation:

dγ

∂θ

∂t



∇·(uθ) =



∇·



Re Pr



∇θ



− γu

(17)

with modiﬁed boundary conditions

φ (x,t) = φ (x + L

,t),φ =u,p, and θ

and

−



∇θ ·n =−1 + γe

·n

Sunden CH006.tex 10/9/2010 15: 39 Page 223

Time-accurate techniques for turbulent heat transfer analysis 223

0 5 15 2010

Time

5.5 × 10

−4

5.4 × 10

−4

5.3 × 10

−4

5.2 × 10

−4

5.1 × 10

−4

5.0 × 10

−4

Time-dependent formulation

Quasi-steady formulation

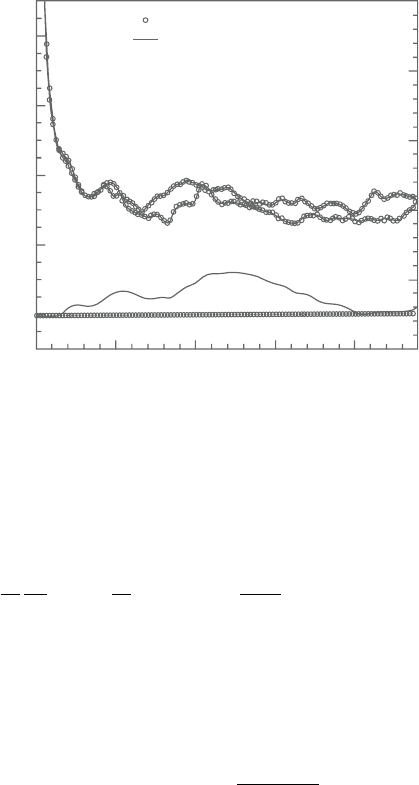
Figure 6.1. Time evolution of γ using the unsteady and quasi-steady procedure.

The time-varying Nusselt number calculated on the two walls is

identical between the two formulations.

The time evolution of γ is obtained by a global integration of equation (17).

Under impermeable wall conditions



dγ



∂θ

∂t

d

=−



RePr

(−1 + γe

·n)d

− γQ

(18)

where 

is the ﬂuid volume in the computational domain, 

is the heat transfer

surface area, and Q

is thex-directional ﬂow rate.Theleft-hand side represents the

time-dependent terms and under assumed quasi-steady conditions the expression

for γ is given as:

γ =



RePrQ

(19)

which represents an instantaneous energy balance between the heat added to the

domain at heat transfer surfaces and that removed volumetrically by the (sink)

term in the energy equation (−γu

). The reduction of equation (18) to (19) uses



e

·nd

=0 for closed heat transfer surfaces.

Figure 6.1 plots the time variation of γ in the heat transfer calculations of tur-

bulent channel ﬂow at Re=Re

=180 (based on friction velocity u

and channel

half-widthδ).Inonecalculation, γ iscalculatedbasedonthetime-dependentevolu-

tion using equation(18) and in theotherit is based onthe quasi-steady assumption

given byequation (19).The temperature ﬁeld is initiated atTime=0 with constant

heat ﬂux boundary conditions at the channel walls after the turbulent velocityﬁeld

Sunden CH006.tex 10/9/2010 15: 39 Page 224

224 Computational Fluid Dynamics and Heat Transfer

is fully developed. Whereas the quasi-steady formulation is affected by the instan-

taneous variations in the ﬂow rate, the unsteady formulation exhibits near constant

values of γ. In spite of these differences, the instantaneous average Nusselt num-

bersbasedonchannelhalf-widthonthetwochannelwallsareidenticalbetweenthe

two calculations.From theseand othersimilar results,the quasi-steadyassumption

in calculating γ can be deemed adequate for most cases when there is no extreme

drivingunsteadinessintheappliedwallheatﬂuxorintheappliedpressuregradient.

6.2.2 Modeling turbulence

For turbulent ﬂows, the appropriate ensemble averaged equations for RANS or ﬁl-

tered equations for LES are constructed in physical space to obtain the Reynolds

stress terms and the subgrid terms, respectively. For a RANS formulation the

Reynolds stresses to be modeled take the form:

[τ];τ

= u



(20)

whereas the subgrid stresses take the form:

[τ]τ

= u

− u

+ u



+ u



+ u



Or τ

= u

−u

(21)

where the overbar represents the Reynolds-averaging operator for RANS and the

ﬁlteringoperationforLES,respectively. InﬁlteringtheLESequationsitisassumed

that the ﬁlter is commutative, i.e.,

∂f /∂x =∂f /∂x. Similarly, u



represents the tur-

bulent ﬂuctuating quantities for RANS and u



the unresolved subgrid velocities.

In equation (21) the underlined term is the Leonard stress term, which denotes

interactions betweenthe resolvedscales contributingto subgrid terms, followedby

the interaction between grid and subgrid scales, and between subgrid scales only.

Withintheframeworkofalinearisotropiceddy-viscositymodelforincompressible

ﬂow, both stress tensors are modeled as:

= τ

−

=−

(22)

where 1/Re

is the nondimensional turbulent eddy viscosity for RANS and

the subgrid eddy viscosity for LES and

=1/2(∂u

/∂x

+ ∂u

/∂x

)or[S] =

1/2





∇

u +



∇u



is the mean or ﬁltered strain rate, respectively. The energy

equation is treated analogously to the momentum equations to give

=−

∂T

∂x

=−



∇

T (23)

wherePr

istheturbulentPrandtlnumber.Forconvenience,intherestofthechapter

the overbar notation is dropped in the rest of the chapter being mindful of the fact

that the same set of equations are used for RANS and LES, which are ensemble

averaged for RANS and ﬁltered for LES.

Sunden CH006.tex 10/9/2010 15: 39 Page 225

Time-accurate techniques for turbulent heat transfer analysis 225

6.3 Transformed Equations in Generalized Coordinate

Systems

For generalization to complex geometries, equations (10–12) are mapped from

physical coordinates (x) to logical/computational coordinates (



ξ) by a boundary

conforming transformation x =x(



ξ), where x =(x,y,z) and



ξ =(ξ,η,ζ). Based on

thedevelopments inThompsonetal. [4], asetofcovariantbasis vectorsaredeﬁned

which are tangents to the coordinate curves ξ

a

=x

, i = 1,2,3

Also deﬁned is the symmetric covariant metric tensor



G, whose elements are

=a

·a

= g

where

√

g =

det|g|=a

·(a

×a

) is the Jacobian of the transformation, which

is the ratio of element volume in physical space to that in computational space.

Deﬁned further are a set of contravariant vectors that are perpendicular to

coordinate surfaces, ξ

=const.,

a



∇ξ

√

(a

×a

), i = 1,2,3 and (i,j,k) are cyclic

where

√

ga

is a measure of the area of the coordinate surface ξ

=const. The

corresponding symmetric contravariant metric tensor with elements:

=a

·a

= g

is then deﬁned.

Under these transfor mations the conservative divergence operator is deﬁned as



∇·



A =

√

∂

∂ξ

(

√



A ·a

), i = 1,2,3

the conservative gradient operator as



∇φ =

√

∂

∂ξ

(

√

ga

φ), i = 1,2,3

and the conservative Laplace operator as:



∇·



∇φ =

√

∂

∂ξ



√

∂

∂ξ

(

√

φ)



, i,k = 1,2,3