Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics
Подождите немного. Документ загружается.


Sunden CH005.tex 10/9/2010 15: 0 Page 186
186 Computational Fluid Dynamics and Heat Transfer
1
2
8
7
6
5
4
3
Streamline
f
down
x
z
y
f
up
D
S
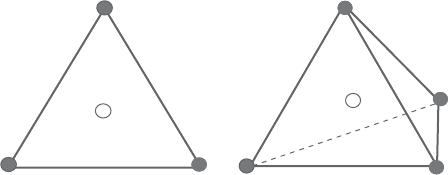
Figure 5.2. Streamline upwind approach for 3D brick element.
where
h
1
=a ·
V, h
2
=
b ·
V, h
3
=c ·
V (29)
Takinganexampleofaeight-node brickelement,theelementdirectionvectors,
a =(a
x
,a
y
,a
z
),
b=(b
x
,b
y
,b
z
), and c=(c
x
,c
y
,c
z
) are calculated using the brick
element nodal coordinates as shown in Figure 5.2.
a
x
=
1
2
(x
2
+ x
3
+ x
6
+ x
7
− x
1
− x
4
− x
5
− x
8
)
a
y
=
1
2
(y
2
+ y
3
+ y
6
+ y
7
− y
1
− y
4
− y
5
− y
8
)
a
z
=
1
2
(z
2
+ z
3
+ z
6
+ z
7
− z
1
− z
4
− z
5
− z
8
)
b
x
=
1
2
(x
5
+ x
6
+ x
7
+ x
8
− x
1
− x
2
− x
3
− x
4
)
b
y
=
1
2
(y
5
+ y
6
+ y
7
+ y
8
− y
1
− y
2
− y
3
− y
4
)
b
z
=
1
2
(z
5
+ z
6
+ z
7
+ z
8
− z
1
− z
2
− z
3
− z
4
)
c
x
=
1
2
(x
1
+ x
2
+ x
5
+ x
6
− x
3
− x
4
− x
7
− x
8
)
c
y
=
1
2
(y
1
+ y
2
+ y
5
+ y
6
− y
3
− y
4
− y
7
− y
8
)
c
z
=
1
2
(z
1
+ z
2
+ z
5
+ z
6
− z
3
− z
4
− z
7
− z
8
)

Sunden CH005.tex 10/9/2010 15: 0 Page 187
Equal-order segregated finite-element method 187
Diffusion term
The diffusion term is obtained by integration over the problem domain after it is
multiplied by the weighting function.
[A
diffusion
e
] =
&
N
∂
∂x
φ
∂φ
∂x
d
e
+
&
N
∂
∂y
φ
∂φ
∂y
d
e
+
&
N
∂
∂z
φ
∂φ
∂z
d
e
(30)
Once the derivative of φ is replaced by the nodal values and the derivatives
of the weighting function, the nodal values will be removed from the integrals,
∂φ
∂x
=
∂N
i
∂x
φ, for momentum equations, the diffusion terms in x,y,z direction are
treated in similar fashion, a typical diffusion item in momentum equation will be
K
ij
=
/
e
µ
∂N
m
∂x
j
∂N
n
∂x
i
d
e
.
Source term
Source term consists of merely multiplying the source terms by the weighting
function and integrating over the volume as follows:
S
e
φ
=
&
N
i
S
φ
d
e
(31)
5.3.3 Stabilized method
Thedifficultiesmostlyencounteredinfinite-elementmethodarefromthemeshthat
isgenerated bygeneralautomatic meshengine. Given athree-dimensional compli-
cated geometry, which is usually from CAD package, e.g., the amount of elements
for automatic generated purely brick could be huge and makes the model analysis
impractical. So hybrid meshes are practically used, but this approach involves lot
of nonbrick elements such as tetrahedron, wedge, and pyramid.This also happens
in two-dimensional hybrid element with quadrilateral and triangle elements.
However,since allthetwo-dimensional andthree-dimensionaldegeneratedele-
mentsdonotsatisfytheLBBcondition, thefluidflowvelocityandpressuresolution
gets locked. The LBB condition restricts the type of element that can be used for
theGalerkinFEMformulation. Bothtwo-dimensionallineartriangularelementand
three-dimensionallineartetrahedral,wedge,andpyramidelementdonotsatisfythis
condition.
Approaches to handle LBB condition
Therearetwoapproachestoovercometheabovedifficulties:oneistousehigh-order
elements and the other to use stabilized FEM based on mixed formulation.
Approach one: high-order elements. High-order elements use midside nodes to
perform quadratic interpolation over elements, but the big disadvantage is that the
total unknowns will increase greatly due to the extra mid-nodes at the element
edges, making the model size limitation to be more restricted – for this reason, the
high-order element is rarely used in commercial finite-element codes.

Sunden CH005.tex 10/9/2010 15: 0 Page 188
188 Computational Fluid Dynamics and Heat Transfer
Approach two: stabilized mixed FEM formulation. Although the mixed for-
mulation requires the elements to be LBB type, there are lot of research work and
effortstodevelop newtechniquesthat circumventthis restriction.Thesetechniques
includebubblefunctionmethod,two-levelmeshmethod,andtheGLSformulations.
These techniques allow the usage of those types of elements that do not satisfy the
LBB condition, such as two-dimensional triangular element (linear velocity/linear
pressure) and three-dimensional tetrahedron, wedge, and pyramid element (lin-
ear velocity/linear pressure interpolation); this is also referred to as equal-order
formulation.
Step 1: Taking three-dimensional incompressible flow as an example for the
mixed FEM–based fluid flow formulation:
⎧
⎪
⎪
⎨
⎪
⎪
⎩
F
1
F
2
F
3
0
⎫
⎪
⎪
⎬
⎪
⎪
⎭
=
⎡
⎢
⎢
⎣
M0 00
0M00
00M0
0000
⎤
⎥
⎥
⎦
⎧
⎪
⎪
⎨
⎪
⎪
⎩
˙u
1
˙u
2
˙u
3
˙
P
⎫
⎪
⎪
⎬
⎪
⎪
⎭
+
⎡
⎢
⎢
⎣
C(u) 000
0C(u) 00
00C(u) 0
0000
⎤
⎥
⎥
⎦
⎧
⎪
⎪
⎨
⎪
⎪
⎩
u
1
u
2
u
3
P
⎫
⎪
⎪
⎬
⎪
⎪
⎭
+
⎡
⎢
⎢
⎣
2K
11
+ K
22
+ K
33
K
12
K
13
−Q
1
K
21
K
11
+ 2K
22
+ K
33
K
23
−Q
2
K
31
K
32
K
11
+ K
22
+ 2K
33
−Q
3
−Q
T
1
−Q
T
2
−Q
T
3
0
⎤
⎥
⎥
⎦
⎧
⎪
⎪
⎨
⎪
⎪
⎩
u
1
u
2
u
3
P
⎫
⎪
⎪
⎬
⎪
⎪
⎭
(32)
A more compact form of this equation is given as
M0
00
$
˙u
˙
P
%
+
C(u) + K(u) Q
T
−Q
T
0
$
u
P
%
=
$
F
0
%
(33)
or in a more symbolic format as
M
˙
U + KU = F (34)
Thenatureofthematrixissparse,generallyunsymmetric,andpositivesemidefi-
nite.Thezeroentriesonthediagonalofthematrixleadtodifficultiesforthesolution
ofthesystemofalgebraicequations. Directsolverneedstohavepivotingtechnique.
Step2:Implementationofequal-orderelementsforthemixedFEM–basedcode
first, in terms of the implementation of so-called bubble function to stabilize the
scheme.
In this approach, the basic formulation is still the Galerkin FEM, but velocity
interpolation is carried out with one additional DOF, which is the centroid of tri-
angular element (2D) and tetrahedral element (3D). The bubble function for the
central node velocity can be chosen as a piecewise linear, with its value being zero
at the element boundaries and piecewise linear on two-dimensional subtriangles
Sunden CH005.tex 10/9/2010 15: 0 Page 189
Equal-order segregated finite-element method 189
Figure 5.3. Bubble function for linear triangular and tetrahedral elements.
or three-dimensional subtetrahedron. The pressure is interpolated linearly over the
element (Figure 5.3).
Step 3: Implementation of stabilized FEM formulation GLS for two-
dimensional and three-dimensional fluid flow using two-dimensional and three-
dimensional degenerated elements, i.e., using equal-order interpolation (linear
velocity/linear pressure) for both velocity and pressure.
The GLS variation form of the momentum and continuity equation is given by
&
w · (ρ
0
u ·∇u)dx +
&
∇w · (−P + 2µD(u))dx −
&
ρ
0
wfdx + Q∇·udx
+
nel
n=1
&
n
R
GLS
dx =−
&
wT
i
ds (35)
Here, w and Q are the weight functions for the momentum equation and the
continuity equation, respectively.The element residual is defined as
R
GLS
= (τ
SUPG
ρ
0
u ·∇w +τ
PSPG
∇Q − τ
GLS
2µD(w))
· (ρ
0
u ·∇u +∇P − 2µD(u)) (36)
The τ coefficients are weighting parameters, which could be functions of the
element size, element Reynolds number, and/or element average velocity. If these
coefficients are selected properly, equal-order elements can be used and LBB
condition is not necessary.
For momentum equation, the final equations are given by
(C(u) + C
SUPG
(u) + C
GLS
(u))u + (K +K
SUPG
+ K
GLS
)u
−
(
Q +Q
SUPG
+ Q
GLS
)
P=F (37)
For continuity equation, we have
−Q
T
u −Q
PSPG
P +C
PSPG
(u)u + K
PSPG
u = 0 (38)

Sunden CH005.tex 10/9/2010 15: 0 Page 190
190 Computational Fluid Dynamics and Heat Transfer
Galerkin/least-squares formulation
The stability of the mixed Galerkin finite element for incompressible flows can be
enhanced by the addition of various least-squares terms to the original Galerkin
variational statement. The Galerkin/Least-squares approach is sometimes termed
a residual method because the added least-squares terms are weighted residuals
of the momentum equation; this form of the least-squares term implies the con-
sistency of the method since the momentum residual is employed. The GLS – a
Petrov–Galerkin method – is also known as a perturbation method since the added
terms can be viewedas perturbations to theweightingfunctions.Developmentand
popularization ofthe GLSmethods for flowproblemsareprimarilydue toHughes,
Tezduyar, and co-workers and are a generalization of their work on SUPG and
PSPG methods.
The usualapproach to theGLS beginswith the discontinuousapproximation in
time Galerkin method and considers a finite-element approximation for a space–
time slab. Continuous polynomial interpolation is used for the spatial variation
whileadiscontinuoustimefunctionisusedwithinthespace–timeslab.Theassumed
time representation obviates the need to independently consider time integration
methods.To simplifythe presentdiscussionof theGLS,thetimeindependent form
of the incompressible flow problem is considered which avoids the complexity of
the space–time finite-element formulation. Using vector notation and following
the weak form development, the GLS variational form for the momentum and
continuity equations can be written as
&
N
m
(ρu ·∇u)dx +
&
∇N
m
· ( −P +2µ∇D(u)dx −
&
ρN
m
f
x
dx +
&
N
n
∇·u)dx
+
nel
n=1
&
R
GLS
=−
&
N
m
τ
i
dsdx (39)
where N
m
and N
n
are the weight functions for the momentum and continuity
equations and the element residual is defined by
R
GLS
= (δ + ε +β) ·(ρu ·∇u +∇(P − 2µ∇D(u)) (40)
δ =τ
SUPG
u ·∇N
m
ε =τ
PSPG
1
ρ
∇N
n
β =−τ
GLS
2µ∇(D(N
m
))
The τ coefficients are weighting parameters; if the definitions for δ,ε, and β
are substituted into equation (40) and the various weighting parameters are made
equivalent to a single parameter τ, the R
GLS
will be
R
GLS
= τ[ρu ·∇N
m
+∇N
n
−2µ∇·D(u)]· [ρu ·∇u +∇(P −2µ∇·D(u)] (41)

Sunden CH005.tex 10/9/2010 15: 0 Page 191
Equal-order segregated finite-element method 191
This isthe standard definitionfor the residualcontribution to theGLSformula-
tion.The splitting of the first residual into three separate contributions in equation
(41) was done to allow the original SUPG and PSPG formulations to be easily
recovered.
If β and ε are set to zero, the stabilized SUPG method is recovered.
If β and δ are set to zero, the stabilized PSPG method is recovered.
If only β is set to zero, both SUPG and PSPG stabilization methods are
recovered.
Notethatin equation(39)thefirstfourintegralsand theright-handsidedefine a
standardGalerkin-weightedresidualmethod thatiswrittenintermsofglobalshape
functions; the integrals are over the simulation domain which is composed by the
discretizedfinite elements.Theaddedresidualterminequation(39)isdefined over
the interior of each element and basically contains the square of all or parts of the
momentum residual. The various τ parameters are positive coefficients that have
the dimension of time. The forms of these parameters are usually developed from
errorestimates, convergenceproofs, anddimensionalanalysis.Particularconstants
within each parameter are selected by optimizing the method on simple problems
and generalizing to multidimensions. It should be noted that the development of
the τ parameters is not a unique process. For the steady problems considered here
a typical τ for the GLS method is
τ =
2
u
h
2
+
4ν
h
2
2
−1/2
(42)
where h is an appropriate element length. For the SUPG and PSPG formulations,
the τ values are the function of an element Reynolds number and the ratio of an
element length to a velocity scale.
The error and convergence analyses for the GLS and PSPG methods have
demonstrated that the equal-order velocity and pressure interpolation for these
methods is viable and the LBB condition is not required [6]. In finite-element
implementation, convenient elements, such as the bilinear Q1/Q1, linear P1/P1,
biquadratic Q2/Q2, and quadratic P2/P2, are now useful approximations while
being unstable inthe Galerkin finite-elementcontext.Thelow-orderelements have
an advantage over their higher-order counterparts because some of the stabiliza-
tion terms associated with viscous diffusion are identically zero.This considerably
simplifies the element equation building process.
The matrix form of velocity–pressure equations
The matrix form of the stabilized GLS formulation could be summarized as the
Momentum equation and Continuity equation, respectively.
Momentum: (C(u)+C
δ
(u)+C
β
(u)}u+(K +K
δ
+K
β
)u−(Q +Q
δ
+Q
β
)P =F
Continuity: −Q
T
u−Q
ε
P +(C
ε
(u)+K
ε
)u=0
Expended discretization form of equations for velocity–pressure coupling and
SUPG stabilization, which are summarized in Table 5.3, will be used as the base

Sunden CH005.tex 10/9/2010 15: 0 Page 192
192 Computational Fluid Dynamics and Heat Transfer
Table 5.3. Element-level matrices
M =
&
e
ρN
m
N
n
d
e
C(u)=
&
e
ρN
m
¯u
j
∂N
n
∂x
j
d
e
Su(u)=
&
e
ρτ
s
¯u
i
∂N
m
∂x
i
¯u
j
∂N
n
∂x
j
d
e
Sp
i
(u) =
&
e
τ
s
¯u
j
∂N
m
∂x
j
∂N
n
∂x
i
d
e
K
ij
=
&
e
µ
∂N
m
∂x
j
∂N
n
∂x
i
d
e
Q
i
=
&
e
∂N
m
∂x
i
N
n
d
e
Sδ
ij
=
&
e
ρδ
∂N
m
∂x
i
∂N
n
∂x
j
d
e
K
τ
i
(u)=
&
e
τ
p
∂N
m
∂x
i
¯u
j
∂N
n
∂x
j
d
e
Q
τ
=
&
e
τ
p
ρ
∂N
m
∂x
j
∂N
n
∂x
j
d
e
SF
i
(u)=
&
e
ρτ
s
¯u
j
∂N
m
∂x
j
d
e
f
bi
SF
4
=
&
e
τ
p
f
bj
∂N
m
∂x
j
d
e
F
i
=
&
∂
e
N
m
i
d
e
+
&
∂
e
ρN
m
f
Bi
d
e
for our further segregated formulation in the next chapter.
⎡
⎢
⎢
⎣
M
1
M
2
M
3
0
⎤
⎥
⎥
⎦
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
˙
ˆu
˙
ˆv
˙
ˆw
˙
ˆp
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
+
⎡
⎢
⎢
⎢
⎣
C(u) + Su(u) Sp
1
(u)
C(u) + Su(u) Sp
2
(u)
C(u) + Su(u) Sp
3
(u)
−K
τ
1
(u) −K
τ
2
(u) −K
τ
3
(u)0
⎤
⎥
⎥
⎥
⎦
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
ˆu
ˆv
ˆw
ˆp
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
+
⎡
⎢
⎢
⎢
⎣
2K
11
+ K
22
+ K
33
K
12
K
13
−Q
1
K
21
K
11
+ 2K
22
+ K
33
K
23
−Q
2
K
31
K
32
K
11
+ K
22
+ 2K
33
−Q
3
−Q
T
1
−Q
T
2
−Q
T
3
0
⎤
⎥
⎥
⎥
⎦
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
ˆu
ˆv
ˆw
ˆp
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
+
⎡
⎢
⎢
⎢
⎣
Sδ
11
Sδ
12
Sδ
13
0
Sδ
21
Sδ
22
Sδ
23
0
Sδ
31
Sδ
32
Sδ
33
0
000−Q
τ
⎤
⎥
⎥
⎥
⎦
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
ˆu
ˆv
ˆw
ˆp
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
=
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
F
1
F
2
F
3
0
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
+
⎧
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎩
SF
1
(
u
)
SF
2
(
u
)
SF
3
(
u
)
−SF
4
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
(43)
It is noted that since all of the SUPG τ parameters depend on the element
size, in the limit as the element size gets smaller, the stabilized method reduces to
Sunden CH005.tex 10/9/2010 15: 0 Page 193
Equal-order segregated finite-element method 193
the Galerkin form. In another words, stabilization plays a significant role only for
coarse mesh.
5.4 Formulation of Stabilized Equal-Order
Segregated Scheme
This section discusses the strategies for the solution of large systems of equations
arising from the finite-element discretization of the formulations. To solve the
nonlinear fluid flow and heat transfer problem, particular emphasis is placed on
segregated scheme in nonlinear level and iterative methods in linear level. The
realityof velocity–pressure couplingformulation inthelast sectionnotonlyresults
inalargedimensionedsystembutalsogeneratesastiffnessmatrixradicallydifferent
to the narrowband type of matrix, which is inefficient to solve and the advection
term causes solution instability.
Thefirstpartinthesectionisthekernelpart;itisauniformedconsistentsolution
scheme for nonlinear and linear level to support any fluid flow/heat transfer and
transport phenomena.The combination of “segregated scheme,” “iterative solver,”
and “BlockI/O”composes the whole solution picture ina very efficientand robust
way. First, the decoupled pressure–velocity segregated scheme is discussed and
expended in very detail under finite-element method by nonlinear level, and then
the Generalized Minimum Residual Method (GMRES)-based iterative technique
andmatrixpreconditionersareusedtosolvelinearequations.Withrespecttoimple-
mentation, thecondensed storageandblockI/Otechniqueis demonstratedto boost
solution efficiency especially for large systems.
5.4.1 Introduction
Several categorizations can be made by using finite-element method to solve the
Navier–Stokes equation for fluid flow and thermal problems. They are mainly
(a) velocity–pressure coupling and (b) orders of interpolation functions for
velocity and pressure.
The first categorization is based on how the primitive variables of velocity
and pressure are treated. The solution schemes are categorized into three groups:
velocity–pressure integrated method, penalty method, and segregated velocity–
pressure method. The velocity–pressure integrated scheme treats velocity and
pressuresimultaneously; itneedslessiterationnumberinnonlinearlevel,butlarger
globalmatrixrequireslongerexecutiontimeandalargememoryinlinearlevel;and
usuallyits overall runtime performance is slow.The penalty scheme eliminates the
direct pressure computation by introducing penalty function, thus speeding up the
executiontimeandmemoryrequirement; however,pressurefieldfromsimplepost-
process is not satisfying especially for large Reynolds number fluid flow problem.
Recently, muchattentionhasbeenpaidtothesegregatedvelocity–pressurescheme,
where velocity and corresponding pressure field are computed alternatively in an
iterativesequence.Thisschemehastheadvantageofspeedandmemoryusagewith
Sunden CH005.tex 10/9/2010 15: 0 Page 194
194 Computational Fluid Dynamics and Heat Transfer
the price of complicated formulation and possible less solution robustness due to
velocity–pressure decoupling (addressed later).
The secondcategorization is basedon the mixed-order interpolation andequal-
orderinterpolationaccordingtotheordersofinterpolationfunctionsforthevelocity
and pressure in element level.The mixed-order interpolation attempts to eliminate
the tendency to produce checkerboard pressure pattern and to satisfy LBB condi-
tion; the velocity in this method is interpolated linearly, whereas the pressure is
assumed to be constant; this interpolation is referred to as Q1P0. The equal-order
interpolationin Ref. [5]useslinear interpolation forvelocity–pressureformulation
(referred to as Q1P1) without exhibiting spurious pressure modes, by employing
nonconsistent pressure equations (NCPEs) for pressure correction. This method
makes the solver more effective than constant element pressure in an element for
Q1P0 method.
Theobjectiveofthischapter istoexplorefurtherthemeritsofthefinite-element
methods in simulating the flow where the upstream effects play important roles.
Thus, we are presenting the details of making use of both the segregated velocity–
pressure and equal-order formulations on the basis of SUPG method.
The basic idea of segregated algorithms is to decouple the pressure calculation
from the velocity calculation by taking the divergence of the vector momentum
equation and applying some clever insights regarding incompressible flow. Early
motivationforthisapproachwaslargelytwofold: tomitigatememoryrequirements
of fully coupled algorithms and to enable semi-implicit time integration.
Pressure–velocity segregation methods have been reviewed by several
researchersin thecontextofthefinite-element method; mostnotableare thepapers
by Gresho and Haroutunian et al. [2]. Basically, all current segregated algorithm
variants are distinguished by the way in which the pressure is decoupled and pro-
jectedfromonetimesteptothenext.HaroutunianandEngelman[2]proposedthree
consistent finite-element counterparts to the SIMPLE and SIMPLER algorithm.
To further reduce the size of the submatrix systems, each individual component
of the momentum equations was solved separately and successively by iterative
techniques. Overall at each Newton iteration or Picard iteration they solved four
matrix subsystems, one for each of three velocity components and one for the
pressure. Interestingly, the most challenging matrix system to solve happens to be
one arising from the discretization of the pressure equation; here, the right-hand
side SF
4
in equation (5.43) is lagged from the last iteration so that this equation
is solved solely for the pressure. The resulting matrix, despite being symmet-
ric, is actually very poorly conditioned due to poor scaling. Nonetheless, these
challenging matrix systems can be readily solved by modern iterative solvers and
reordering/preconditioner strategies, andthesuccess of this algorithm over thelast
decade has been enormous.
In our view this approach is still a compromise to the favorable convergence
properties ofafullycoupledtechnique advocated here.Convergencetostablesolu-
tions at successive time steps is linear at best case and sometimes asymptotic,
sometimes resulting in large number of required segregation iterations (albeit fast
iterations). Moreover, the method introduces several relaxation parameters that
Sunden CH005.tex 10/9/2010 15: 0 Page 195
Equal-order segregated finite-element method 195
must be tuned to the application. If one chooses alternatives to the primitive vari-
able formulation, then boundary conditions on velocity become challengeable to
applyaccurately. Finally, codescenteredaroundthisalgorithmaremorecomplexin
structure, as they stillcontain theintricacies ofmatrixsolutionservicesbut involve
morethan onedatastructure(for themixedinterpolation) andmoreinner andouter
iteration loops.
5.4.2 FEM-based segregated formulation
ThisformulationisbasedonthealgorithmofRiceandSchnipke’s[5]andShaw’s[7]
pioneerworks;theyuse non-consistentpressure equations(NCPE)forthepressure
stepandpressurecorrectionstepratherthantheconventionalweakformoftheflow
equations resultingfrom Galerkin finiteelement context.This approach hasgained
popularity inrecent yearswith the very desirable advantage of precludingspurious
pressure modes from pressure solution. This consequently allows them to employ
the desirable feature of “equal-order interpolation for the velocity and pressure.”
Forthisreason, the algorithmcan solvethe flow withoutusing very refinedmeshes
andhybridelementtypeshighlydesirableforcommercialcodeobtainedfromCAD
model. However, the expanse ofthis algorithmincludes theextrawork ofimposing
boundary conditions properly and their complex formulation. In this section, we
show the formulation derivation details starting from the N–S equation.
Bilinear interpolation
The fluid flow continuity equation and the momentum equation follow same form
as listed in Section 3.1. For implementation using finite-element method, velocity
and pressure at arbitrary position could be interpolated using “equal-order bilinear
interpolation” to adapt brick or other degenerated elements.
u(x,y) = N
i
u
i
(44a)
v(x,y) = N
i
v
i
(44b)
w(x,y) = N
i
w
i
(44c)
p(x,y) = N
i
p
i
(44d)
Discretization and system assembly
Using the standard Galerkin approach, the momentum equation is multiplied by
weighting functions, and using the Green–Gauss theorem, the diffusion terms are
integrated by parts in x momentum equation as follows:
&
ρN
u
∂u
∂x
+ v
∂u
∂y
+ w
∂u
∂z
d =−
&
N
∂p
∂x
d +
&
NF
x
d
(45)
+ µ
&
N
∂
2
u
∂x
2
+
∂
2
u
∂y
2
+
∂
2
u
∂z
2
d
