Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics

Подождите немного. Документ загружается.

Sunden CH005.tex 10/9/2010 15: 0 Page 206

206 Computational Fluid Dynamics and Heat Transfer

XXX

XX XX

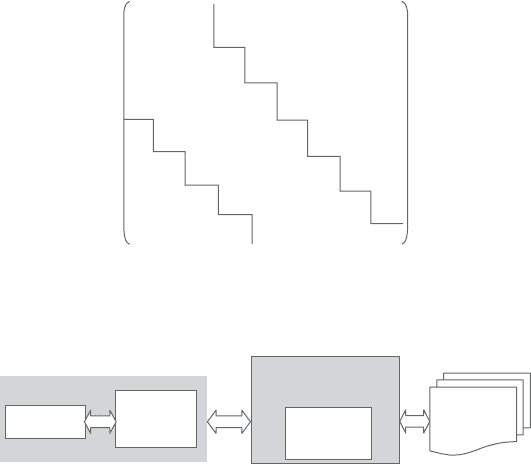
Figure 5.5. Skyline matrix structure.

Program

buffer

Operation system

area

System

cache

Output

file

Figure 5.6. Block buffer I/O for disk writing.

Block I/O process

Improving overall disk I/O performance can minimize both device I/O and

actual CPU time. The techniques listed here can signiﬁcantly improve FEA code

performance.

Theslowestprocess(routines)couldbedetectedbyusingproﬁlingtoolssuchas

AQTIME.Afterrunning a typical size of FEA model, the routinesusingmost time

in analysis, the top routines, and even lines are the processor bottleneck.These are

the targets to be improved for better perfor mance.

“Block I/O” is a cost-efﬁcient record buffer technique for large amount of data

in the FEA processor. For writing, it saves a ﬁxed number of element matrix infor-

mation into buffer, and then writes the whole buffer into disk if the buffer is full,

whereasreading isthe reverse procedure.Thebuffersize isrelated to ﬁlesystem in

operation system and disk cache; we found that the optimal buffer size is 8 kbytes

for Windows XP WIN32 NTFS ﬁle system.

Here is an example for storage size calculation of one block element stiffness

matrix with three-dimensional brick element (eight nodes) (Figure 5.6).

Block size

=128 matrices* (8*8 entries/matrix) * 8 bits /entry

=65,536 bits

=65,536/8 bytes

=8,192 bytes

Sunden CH005.tex 10/9/2010 15: 0 Page 207

Equal-order segregated ﬁnite-element method 207

Table 5.4. Data structure for Block I/O

Part ID Element type Data mapping Block numbers

Simulation Part 1 Tetrahedral Block 1 (32 kB) 6 blocks

domain elements Block 2

(4 nodes) Block 3

Block 4

Block 5

Block 6 Block 6

Other Block 1 (32 kB) 5 blocks

hybrid Block 2

elements Block 3

(8 nodes) Block 4

Block 5 Block 5

Part 2 Tetrahedral Block 1 (32 kB) 7 blocks

elements Block 2

(4 nodes) Block 3

Block 4

Block 5

Block 6 (32 kB)

Block 7 Block 7

Other hybrid Block 1 (32 kB) 3 blocks

elements Block 2 (32 kB)

(8 nodes) Block 3 Block 3

ThedatastructureforblockbufferI/OisshowninTable5.4.Theﬂuiddomainis

composedofmultipleparts,whileeachpartis decodedastheagroupof tetrahedral

elements and the a group of hybrid elements, hybrid element could be the com-

bination of any brick, pyramid, wedge elements which could be considered as the

degraded element from eight-node brick element. For each group, 128*4 matrices

from tetrahedral element composed a block; each matrix has 4*4 element entries,

which also has the block size of 8 kbytes.

Because the ﬂuid domain is composed of parts and each part has a different

number of brick element and tetrahedral element while the number may not be the

eventimes oftheoptimalblockelementnumber,aspecialcounterwasusedifthere

were a remainder of element number over block size number.

Sunden CH005.tex 10/9/2010 15: 0 Page 208

208 Computational Fluid Dynamics and Heat Transfer

Apart from the efﬁcient use of record buffers and disk I/O, some other tips as

the following were used in the code implementation:

(a) Using unformatted ﬁles instead of formatted ﬁles.

(b) Writing whole arrays.

By using the above-mentioned comprehensive methods, the I/O performance

can be dramatically improved, but when compared to other operations, it becomes

trivial.

5.5 Case Studies

This section shows two examples of conjugate heat transfer problems where both

solid and ﬂuid are involved in the heat transfer analysis. The results are obtained

byusingﬁnite element–basedequal-order segregatedsolution schemediscussed in

this chapter, and the SUPG stabilization term is enforced in both ﬂuid and thermal

processors.

For simple geometry, the high cell Peclet number did not cause severe problem

for the simulation results. That is because the temperature gradient in the ﬂow

direction happened to be small for the natural boundary condition applied at the

exit. Consequently, the numerical diffusion introduced by the discretization also

becomes small. For complexgeometry, however, heat transfer occurs through both

convection and diffusion in all directions. Whenever the convection effects are

strong, the numerical oscillation of the computed temperature would happen if the

Galerkin formulation were used.

The reason for this numerical difﬁculty has been well described. The conclu-

sion basically is that the Galerkin formulation is of the same nature as the central

ﬁnite difference scheme. It does not consider the inﬂuence of the ﬂow velocity on

the temperature distribution in a cell through its basic interpolation functions. To

overcome this difﬁculty, either an upwind scheme or optimized upwind scheme

(SUPG) should be adopted for the convection term. In the upwind schemes, a bias

is given to the upwind nodal temperature by modifying the interpolation functions

according to the local ﬂuid ﬂow velocity, both the direction and the magnitude.

5.5.1 Two-dimensional air cooling box

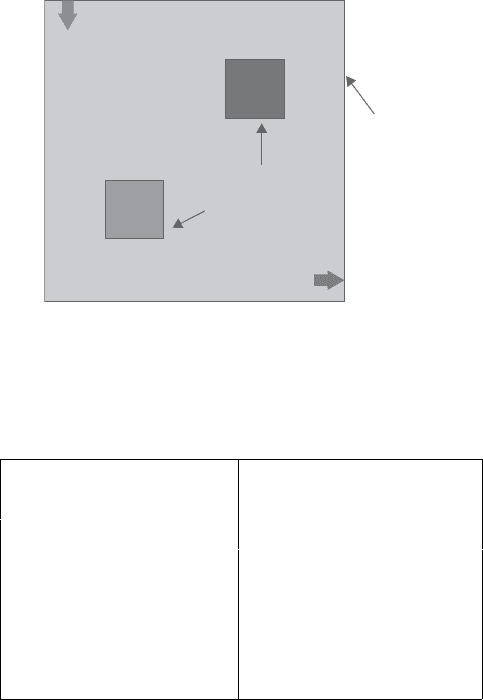
TheﬁrstexampleshowninFigure5.7isatwo-dimensionalsquare-shapedelectronic

boxwith airﬂow cooling.Twosmall copper blocks are heat sourceswith a constant

volumetric heat generation rate. The airﬂow comes in from an opening at the top

edge near the left corner, and the outlet is located at the right side edge near the

bottom corner. The ﬂow rate and the temperature at the inlet are speciﬁed. The

inﬂuence of the inlet ﬂow rate on the maximum temperature in the entire system,

Sunden CH005.tex 10/9/2010 15: 0 Page 209

Equal-order segregated ﬁnite-element method 209

Outlet

Inlet

cooling air

T  25°C

Heat

generation

blocks

Convection

boundary

Figure 5.7. Schematicillustrationforairﬂowcoolingintwo-dimensionalelectronic

case.

Table 5.5. Summaryofparametersforairﬂowcoolingsystem

Inlet velocity U 0.01 or 0.001 (m/s)

Inlet temperature T

25 (

◦

Case dimensions 5by5(mbym)

Heating block 1 (1, 1) to (2, 2) (x, y) – (x, y)

Heating block 2 (3, 3) – (4, 4) (x, y) – (x, y)

Convection ﬁlm coefﬁcient 0.2 (J/m

◦

Ambient temperature 25 (

◦

Heat generation rate 20 (J/s/m

)

caused by the twoheat sources, can bepredicted.Toverify theeffects ofthe SUPG

formulation, this case has also been analyzed using the Galerkin formulation.

The mesh used for the entire domain is 100×100, so the number of elements

for this model is 10,000. Two element g roups are used in order to specify heat

generation rate for the two heat sources. The ﬂow media is dry air and the two

heating blocks are copper. The edges of the two-dimensional box transfer heat

to the ambient atmosphere through the natural convection. The convection ﬁlm

coefﬁcientis assumed as a known value.A summary of the parameters used inthis

case study is given inTable 5.5.

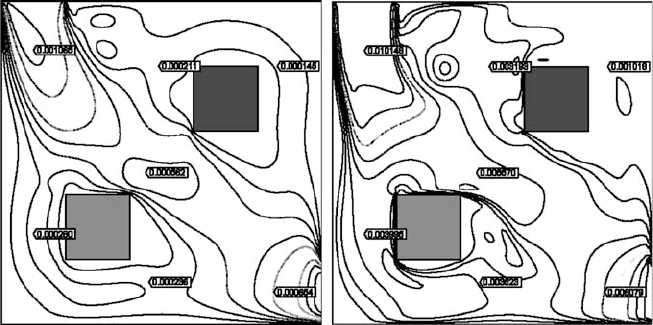
ThecomputedresultsfortwodifferentinletﬂowvelocitiesshowninFigure5.7a

and b are obtained if the simulation was carried out based on the Galerkin formu-

lation. For (a) the cell Peclet number is about 20.0, while for (b) it is about 200.0.

Temperature oscillations in some area of the ﬂow domain may become severer for

the higher cell Peclet number case if SUPG stabilized term is not enforced.

Sunden CH005.tex 10/9/2010 15: 0 Page 210

210 Computational Fluid Dynamics and Heat Transfer

Inlet velocity U  0.001 m/s

(a) (b)

Inlet velocity U  0.01 m/s

Figure 5.8. Velocity isolines in cooling box.

The cooling effect can be observed by comparing Figure 5.8a and b.The result

was achieved by using SUPG stabilized Galerkin discretization; the temperature

oscillations were completely eliminated by the optimized upwind SUPG scheme.

The higher inlet velocity makes more effective cooling result, the maximum

temperature for (a) is about 113.76

◦

C if inlet velocity is 0.001m/s, while for

(b) it is only about 64.50

◦

C if inlet velocity is 0.01m/s. Relatively regular velocity

and temperature patterns are maintained at smaller velocity since the ﬂow stays in

laminar range.With increase in velocity, the ﬂow becomes irregular and more vor-

texes aredeveloped, and the ﬂow convectionmakes thecorresponding temperature

patterns.

Because the inlet velocity enters the box from the top side, the momentum

lets the ﬂow to hit the bottom heat generation block easily. This effect becomes

more obvious with increase in velocity, so that the temperature in the bottom heat

generation block is lower than the top heat generation block even if the two blocks

have the same amount of heat generation rate (Figure 5.9).

5.5.2 CPU water cooling analysis

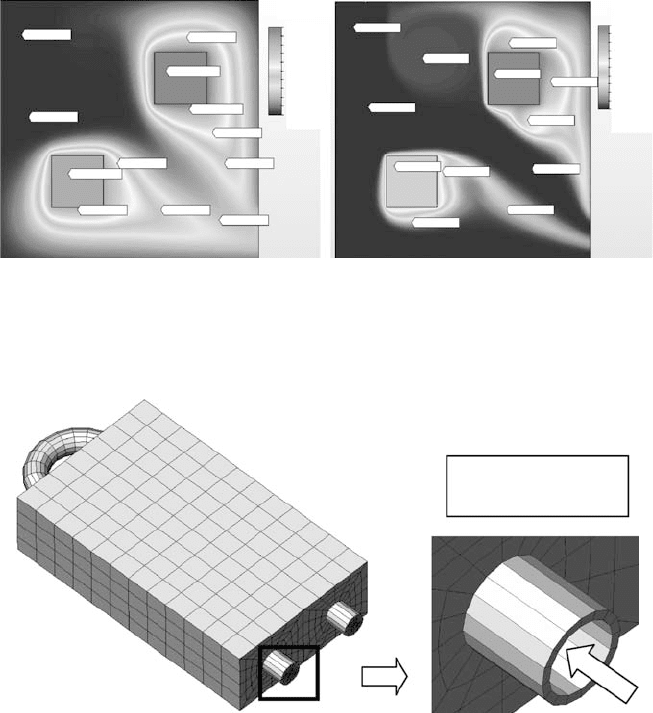
A three-dimensional ﬁnite-elementanalysis is established for a CPUwater cooling

system, as shown in Figure 5.10.The bottom surface of the heat exchange block is

actually in contact with the surface of a CPU chip.

A constant heat ﬂux is therefore speciﬁed for this surface. It is assumed that

the CPU has 130 W power dissipation and the heat is dissipated through the base

surface of the heat exchangeblock. Depending on the surface size and total power,

the heatﬂux boundary condition issetas 38.5. Otherexternal surfacesofthe block

areexposedtotheambientatmospherewithagivenconvectionﬁlmcoefﬁcientof5.

Sunden CH005.tex 10/9/2010 15: 0 Page 211

Equal-order segregated ﬁnite-element method 211

25.000057

80.396443

25.000000

50.908382

45.792520

33.506713

33.527300

25.014191

49.412597

55.707212

64.494155

53.733615

26.881897

Temperature

°C

Temperature

°C

113.7605

104.8845

96.00844

87.13238

78.25633

69.38027

60.50422

51.62816

42.75221

33.87605

64.50332

60.55251

56.6017

52.65089

48.70008

44.77927

40.79846

36.84765

32.89684

28.94603

24.99522

113.755978

104.314131

76.834744

60.974225

47.293483

62.560818

76.045629

101.168845

96.056686

25.008885

Inlet velocity U  0.001 m/s

(a) (b)

Inlet velocity U  0.01 (m/s)

Figure 5.9. Temperature contours in cooling box.

Mesh for the tube

(enlarged view)

Figure 5.10. 3D model for a CPU water cooling system.

The tube wall is also modeled in this analysis, a part of the tube surface is exposed

to the ambient atmosphere, and it has the same convection ﬁlm coefﬁcient as that

of the block surfaces. Both the block and the tube are made of the same material,

which is aluminum in this case.

Coolingwaterwithaveragevelocityof0.06m/satinletgoesthroughthetubeto

convecttheheatoutofthesystem; thevelocityproﬁleinthewatertubeiscalculated

by ﬂuid ﬂow analysis and then passed to thermal analysis as the convection term.

The temperature at the entrance of the tube is speciﬁed as 25

◦

C in the analysis.

The steady-state conjugated heat transferproblem is calculated by using the equal-

order segregatedsolution schemeand SUPGstabilizedtermdiscussed earlier.This

example illustrates effective water cooling in the electronic system.

Sunden CH005.tex 10/9/2010 15: 0 Page 212

212 Computational Fluid Dynamics and Heat Transfer

Temperature

°C

61.75961

58.08365

54.40769

50.73173

47.05577

43.37981

39.70384

36.02788

32.35192

28.67596

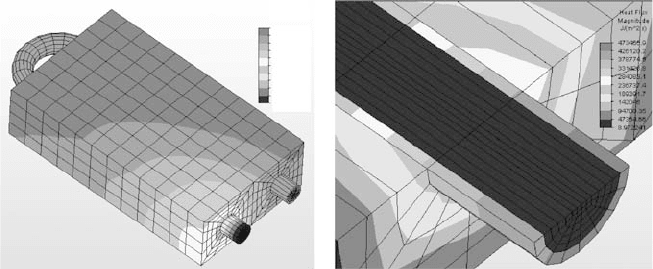
Figure 5.11. Result contour for the CPU water cooling system.

ThecomputedtemperaturecontoursareshowninFigure5.11a.Thetemperature

ranges from 25

◦

Cto61

◦

C. The numerical oscillation of the temperature solution

in traditional Galerkin formulation has been eliminated by using the SUPG term.

This indicates that the SUPG formulation does provide a much better solution

over the Galerkin formulation, especially for convection-dominated heat transfer

problems. The heat ﬂux contour in the vicinity of the cooling ﬂow inlet is shown

in Figure 5.11b. It is noticed that the maximal heat ﬂux is located in the vicinity of

the inlet tube wall, which implies the maximal temperature gradient is there since

the heat ﬂux is proportional to the temperature gradient.

References

[1] Choi, H. G., andYoo, J.Y. Streamline upwind scheme for the segregated formulation

of the Navier-Stokes equation. Numerical HeatTransfer, Part B, pp. 145–161, 1994.

[2] Haroutunian, V., Engelman, M. S., and Hasbani, I. Segregated ﬁnite element

algorithms for the numerical solution of large-scale incompressible ﬂow problems,

International Journal for Numerical Methods in Fluids, 17, pp. 323–348, 1993.

[3] Hill,D.L.,andBaskharone,E.A.Amonotonestreamlineupwindmethodforquadratic

ﬁnite elements, International Journal for Numerical Methods in Fluids, 17, pp. 463–

475, 1993.

[4] Reddy, J. N., and Gartling, D. K. The Finite Element Method in Heat Transfer and

Fluid Dynamics, 2nd Edition, CRC Press, 2000.

[5] Rice, J. G., and Schnipke, R. J. A monotone streamline upwind ﬁnite element

method for convection-dominated ﬂows, Computer Methods in Applied Mechanics

and Engineering, 48, pp. 313–327, 1985.

[6] Rice,J.G.,andSchnipke, R. J.Anequal-ordervelocity-pressureformulationthatdoes

not exhibit spurious pressure modes, Computer Methods in Applied Mechanics and

Engineering, 58, pp. 135–149, 1986.

[7] Shaw, C. T. Using a segregated ﬁnite element scheme to solve the incompressible

Navier-Stokes equations, International Journal for Numerical Methods in Fluids, 12,

pp. 81–92, 1991.

Sunden CH005.tex 10/9/2010 15: 0 Page 213

Equal-order segregated ﬁnite-element method 213

[8] Schunk, P. R., and Heroux, M. A. Iterative solvers and preconditioners for fully-

coupled ﬁnite element formulations of incompressible ﬂuid mechanics and related

transportproblems,SandiaNationalLaboratories,Albuquerque,NewMexico,87185–

0835, 2001.

[9] Tezduyar,T., and Sathe,S.Stabilizationparameters in SUPG and PSPGformulations,

Journal of Computational andApplied Mechanics, 4(1), pp. 71–88, 2003.

[10] duToit, C. G.A segregated ﬁnite elementsolution for non-isothermal ﬂow, Computer

Methods inApplied Mechanics and Engineering, 182(3), pp. 457–481(25), 2000.

[11] Van Zijl, and duToit, C. G. A SIMPLEST ﬁnite element solution of the incompress-

ible Navier-Stokes equations, In: Proc. Symposium of Finite Element Method, South

Africa, 1992.

[12] Vellando, P. On the resolution of the viscous incompressible ﬂow for various SUPG

ﬁnite element formulations, Europeancongress onthe Computational Methodsin the

Applied Sciences and Engineering – (ECCOMAS) 2000, Barcelona, 2000.

[13] Wang, G. A fast and robust variant of the simple algorithm for ﬁnite-element sim-

ulations of incompressible ﬂows, Computational Fluid and Solid Mechanics, 2,

pp. 1014–1016, Elsevier, 2001.

[14] Wang, G. A conservative equal order ﬁnite element method using the collo-

cated GALERKIN approach, 8th AIAA/ASME Thermo-physics and heat transfer

conference, St. Louis, Missouri,AIAA 2002-3206, 2001.

[15] Wansophark, N. Enhancement of segregated ﬁnite element method with adaptive

meshing technique for viscous incompressible thermal ﬂow analysis, Science Asia.

29(2), pp. 155–162, 2003.

[16] Xie, J. Equal-order segregated ﬁnite element formulation for ﬂow and phase change

problems, Doctoral Dissertations, University of Wisconsin, 2007.

This page intentionally left blank

Sunden CH006.tex 10/9/2010 15: 39 Page 215

III. Turbulent Flow Computations/Large

Eddy Simulation/Direct Numerical

Simulation