Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics

Подождите немного. Документ загружается.

Sunden CH006.tex 10/9/2010 15: 39 Page 236

236 Computational Fluid Dynamics and Heat Transfer

equation should satisfy Gauss divergence theorem, i.e.,



D ·(Gp)d



(Gp) ·nd

and



D ·ud



u ·nd

(48)

where D and G are the discrete divergence and gradient operators, u is the nondi-

mensional velocity vector, n is the outward pointing unit normal at the surface 

bounding the computationaldomain of volume

.This simply states thatthedis-

crete divergence operator when summed over the domain must reduce to a surface

integralatthedomainboundaries.Thisisalwayssatisﬁedwhenaﬁnite-volumeform

ofthedivergenceoperatorisusedintheformofequation(42). However,deviations

fromthe effectivelysecond-orderdivergenceoperator(high-orderapproximations)

are difﬁcult to reconcile and result in artiﬁcial mass sources/sinks in the compu-

tational domain and incomplete convergence. It is noteworthy that equation (48)

places no restriction on the discrete gradient operator. Following from equation

(48) isthe additionalcondition that resultsfrom Gaussdivergence theoremapplied

to the discrete pressure equation



(Gp) ·nd

t



u ·nd

(49)

Hence,iftheintermediateincompressiblevelocityﬁeldinthefractionalstepmethod

satisﬁes global mass conservation, which it should, then the LHS of equation (49)

should sum to zero. The use of a zero gradient condition on pressure at inhomoge-

neous boundaries for known boundary velocities is consistent with this equation.

The condition is also satisﬁed at homogeneous or periodic boundaries.

Underthe requirementsofeliminating gridscale oscillationsona nonstaggered

grid and satisfying the integrability constraint and discrete continuity, one formu-

lation that is quite effective is to interpolate the nodal Cartesian velocities to the

cell faces (˜u

) to obtain the contravariant ﬂuxes

√

. However, the interpolated

contravariant cell face ﬂuxes are treated as velocities on a staggered grid and are

corrected by using thecompact form ofthe pressure gradient.The net result ofthis

formulation is that the spuriouspressureterms in equations (45)and(46) are elim-

inated. However, the equivalent nodal momentum equation still carries the burden

of the spurious third derivative pressure term (see equation (41)). In spite of this,

the problem of grid scale oscillations is considerably reduced and in sufﬁciently

well-resolved ﬂows is non-existent.This is referred to as “current formulation” in

the following discussion.

The different formulations are tested in turbulent channel ﬂow at Re

=180 on

a64× 64 × 64 mesh with z

=8.8 and x

=35.2. The pressure spectr um is

Sunden CH006.tex 10/9/2010 15: 39 Page 237

Time-accurate techniques for turbulent heat transfer analysis 237

0.01

0.001

−5

0.0001

1 10 100

0.1

staggered

nonstaggered (L22)

nonstaggered (L23)

nonstaggered (current)

−8

−7

−6

−5

0.01

0.1

0.001

1 10 100

staggered

= 5

= 120

nonstaggered (L22)

nonstaggered (L23)

nonstaggered (current)

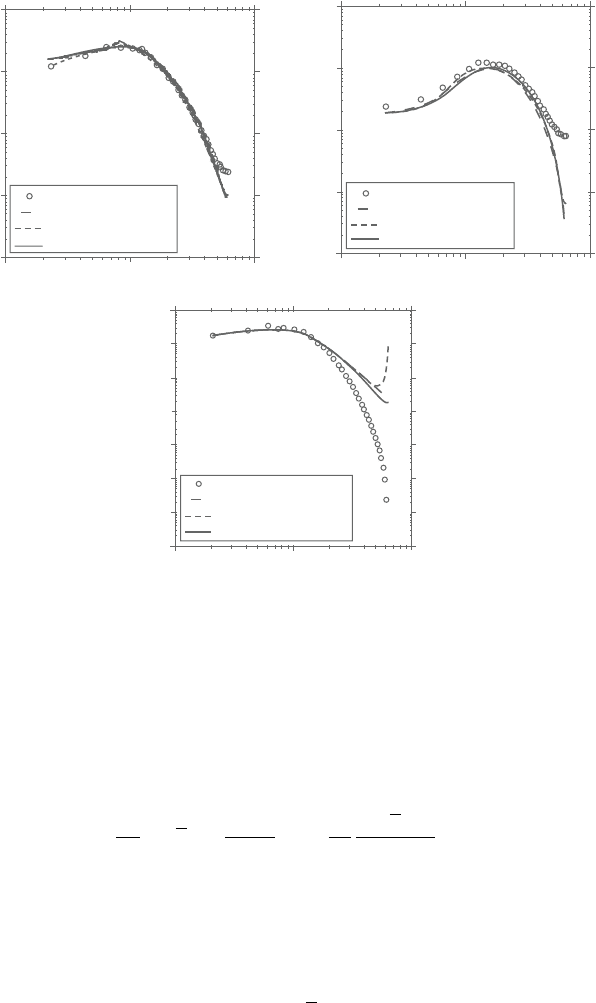
Figure 6.5. One-dimensional pressure spectra in turbulent channel ﬂow at

=180 for different pressure formulations.

calculatednearthe wall aty

=5and toward thecenter ofthe channel aty

= 120

andplottedinFigure6.5.Differentnonstaggeredgridformulationsarecomparedto

thestaggeredgrid. L

isthedefaultnoncompactformoftheLaplacianconstructed

onanonstaggeredgrid[14],L

istheLaplacianconstructedbyTaftietal.[14], and

lastlythe current formulation is shown.The pressure spectrum at the two locations

showthatwhilethereissomeenergyaccumulationinthenear-gridscalesforall the

nonstaggered grid formulations, the current formulation prevents a large buildup.

Between the default formulation L

and the designed formulation L

somewhat better. At the same time, the presence of spurious oscillations near and

at grid scales in pressure do not necessarily carry through to the power spectrum

of the velocity components as seen in Figure 6.6. In fact it is only in the spanwise

velocity that any accumulation of energy is present.

Hence, the following series of steps are used in the corrector step. First, the

intermediate cell face contravariant ﬂuxes are constructed as follows:

√

g(a

)

˜u

(50)

by interpolating the nodal velocities at the cell face. The contravariant ﬂux is then

conserved at nonmatching boundary faces to obtain 

√

. Then, the correc-

tion form of the nodal Cartesian velocities and cell face contravariant ﬂuxes are

written as:

n+1

=˜u

− t(a

)

∂P

n+1

∂ξ

(51)



√

g(U

)

n+1

=

√

−t

√

∂P

n+1

∂ξ

(52)

Sunden CH006.tex 10/9/2010 15: 39 Page 238

238 Computational Fluid Dynamics and Heat Transfer

.01

0.01

0.001

0.0001

100

= 5

Staggered

non-staggered (L

)

non-staggered (L

)

non-staggered (current)

0.01

0.001

0.0001

= 5

−5

−6

100

Staggered

non-staggered (L

)

non-staggered (L

)

non-staggered (current)

.01

0.01

0.001

0.0001

Staggered

non-staggered (L

)

non-staggered (L

)

non-staggered (current)

= 5

−5

−6

−7

−8

100

Figure 6.6. One-dimensional velocity spectra in turbulent channel ﬂow at

=180 for different pressure formulations.

Using the ﬁnite-volume divergence operator in the mass continuity equation to

satisfy the integrability constraint and substituting equation (52) for the cell face

contravariant ﬂuxes, the pressure equation takes the form:

∂

∂ξ



√

∂P

n+1

∂ξ

7

t

∂

√



∂ξ

(53)

The calculated pressure ﬁeld at level n+1 is then used to cor rect the nodal

Cartesian velocities and the cell face contravariant ﬂuxes using equations (51)

and (52), respectively. The use of  on the pressure gradient term implies the

integral conservation of this quantity at nonmatching interf ace boundaries, dur-

ing the solution of equation (53). Hence,

√

g(U

)

n+1

is automatically conserved

when the correction in equation (52) is applied to the conserved intermediate

ﬁeld.

Sunden CH006.tex 10/9/2010 15: 39 Page 239

Time-accurate techniques for turbulent heat transfer analysis 239

6.5.3 Integral adjustments at nonmatching boundaries

To eliminate the buildup of small interpolation errors, integral adjustments at non-

matching interfaces are used for conserved variables. At the beginning of each

time step, momentum and energy ﬂuxes are conserved at nonmatching bound-

aries by imposing the equality of mass or volume ﬂuxes. With reference to

Figure 6.2,





√

φ =





√

φ (54)

in the ξ-η direction, where φ =u

or T are the interpolated values. The equality is

used to obtain the conserved quantity <φ>.

The intermediate contravariant ﬂuxes in equation (50) are ﬁrst calculated from

the interpolated intermediate velocities. The calculated ﬂuxes, however, do not

exactlysatisfytheintegralbalanceacrossthenonmatchinginterface.Theconserved

ﬂuxes 

√

 are obtained by imposing the integral balance across the two faces

as in



√



√

(55)

There are two choices available in imposing equality of the conserved quan-

tity in equation (54). One is proportional scaling and the other is an additive

adjustment. Proportional scaling may have difﬁculties when the mean mass ﬂux

across the boundary is close to zero, whereas additive adjustments may smear

weak recirculation zones at or near the interface. Since most of the time in

a well-resolved ﬂow, the interpolation error is small, the contravariant ﬂux is

adjusted linearly for the sake of robustness. However, for small values of

√

in equation (54), even an additive adjustment has the potential of leading to

instabilities, since to obtain <φ> the total ﬂux needs to be divided by this

quantity.

For the pressure equation (53), the pressure at the ghost cell is ﬁrst inter-

polated from the relevant boundary that serves as a boundary condition for the

interior values. Since in incompressible ﬂows the pressure gradient is the relevant

quantity that drives the ﬂow, this quantity is conserved at nonmatching interfacial

boundaries. For each iteration in the pressure equation solver, the normal gradi-

ent of pressure is ﬁrst evaluated and then integrated over the relevant interfacial

boundary. Based on the difference of the two integral values, a constant value

is then added/subtracted to the pressure at the ghost cells in order to guarantee

the equality of the two integral values. Since this procedure is integrated into the

linearsolutionof thepressure equation, itautomaticallyguarantees anintegral bal-

ance of the contravariant ﬂuxes across nonmatching interfaces calculated through

equation (52).

Sunden CH006.tex 10/9/2010 15: 39 Page 240

240 Computational Fluid Dynamics and Heat Transfer

6.6 Discretization of ConvectionTerms

Byfar,fromthenumericalstandpoint,thediscretizationofthenonlinearconvective

terms has the most profound effect on the accuracy with which turbulence is rep-

resented on a given mesh.An important aspect of turbulent ﬂow simulations is the

roleoftruncationandaliasingerrors, whichusuallymanifestthemselvesinthehigh

wavenumbersoftheresolvedscales.Ideally,thediscretizationshouldhavethecapa-

bility of representing all the g rid-resolved wavenumbers with accuracy, conserve

quadratic quantities such as kinetic energy, have minimal aliasing errors, and be

stableandrobustatthesametime.Whiletruncationerrorscanbedirectlyestimated

fromTaylorseriesexpansionsinphysicalspaceandmodiﬁedwavenumberrepresen-

tationsinwavespace(Lele[17],BeudanandMoin[18]),thequantiﬁcationofalias-

ingerrorsintimeintegrationalgorithmsandtheireffectontheaccuracyandnumer-

ical stability of the algorithm is not straightforward (Kravchenko and Moin [19]).

Themostpopular methodforapproximatingconvectiontermshasbeenanSOC

difference discretization on staggered as well as nonstaggered grids.Although not

perfect, it provides a reasonable and economical alternative to other high-order

schemes.Whenthe SOC scheme is applied to the divergence or conservative form

of the convective terms in a ﬁnite-volume framework, it has the desirable property

of conserving global kinetic energy. Although total kinetic energy is conser ved,

also present is the artiﬁcial redistribution of energy among the resolved scales.

Relatedtothisarealiasingerrorsthatresultfromthespuriousaccumulationofunre-

solvednumericalsubgridenergyintheresolvedscalesduetothehigh-wavenumber

nonlinear interactions of the velocity ﬁeld. Early work in the meteorological and

geophysical community(Phillips [20],Lilly[21], andArakawa[22]) hasaddressed

theroleofaliasinginthedevelopmentofnonlinearnumericalinstabilities,whichled

to the development of global energy-conserving ﬁnite-difference schemes. Global

energy-conserving schemes require that the advection of a constant velocity ﬁeld

should not produce nor destroy global kinetic energy.According toArakawa [22],

thetwoconditionsthat aconvectivedifferencingschemeshould satisfytoconserve

quadratic quantities are:



, j



: i, j,k

=−A

i, j,k :i



, j



i, j,k :i, j,k

= 0

(56)

Theﬁrst equationrequiresthat thediscreteeffectofone nodeonanothershould

be equal and opposite, and the second condition requires that the node should not

inﬂuence itsown value.In 1-D,A

(i)=−A

(i +1)andA

=0,where E,W, and P

refertoathreepointﬁnite-differencestencil.Fortheﬁnite-volumeapproximations,

the ﬁrst condition is always satisﬁed, whereas the second condition is linked to the

satisfaction of discrete continuity in a form that will lead to it being zero. Hence,

the energy-conserving property is inexplicably linked to the consistent solution

of the pressure equation. It can be easily shown that the SOC scheme used with

a consistent second-order construction of the divergence operator will satisfy the

second condition. Any deviation from SOC to high-order approximations requires

that the divergence operator in continuity and pressure be tailored to satisfy the

Sunden CH006.tex 10/9/2010 15: 39 Page 241

Time-accurate techniques for turbulent heat transfer analysis 241

second condition. In fact most other conventional high-order schemes based on

upwinding or central-differencing do not satisfy the second condition and special

considerations have to be given to construct high-order schemes that are energy

conserving (Morinishi et al. [23]).

On the other hand, in spite of not conserving global energy, high-order ﬁnite-

difference schemes have been formulated and used to reduce the truncation errors

associated with the ﬁnite-difference approximations. A number of such formula-

tionshavebeenusedinthepastbasedonhigh-ordercompactdifferences(Lele[17]),

conventional high-order upwind biased approximations (Rai and Moin [24]), and

fourth-ordercentraldifferences.Accompanyingthehigh-orderconvectiveschemes

are also high-orderapproximations of the viscousterms and thepressure equation.

Tafti et al. [25] have investigated a number of high-order schemes based on con-

servative and nonconser vative formulations of the convection term combined with

different pressure equation formulations.

A few of the high-order formulations weretestedfor the numerical simulations

of turbulentchannel ﬂowat Re

=180(based onwallfriction velocityand channel

half-width) using a staggered grid. Results from the 2

22, 5

22, and 5

formulation are compared with the spectral simulations of KMM [6] and experi-

ments of Kreplin and Eckelmann [26] (KE). Here c stands for the conservative or

divergence for m of the convection terms, which is discretized in a ﬁnite-volume

framework,andncstandsforanonconservativeformoftheconvectionterm, which

is discretized using ﬁnite-difference approximations.The ﬁrst number denotes the

order of approximation of the convection term, 2 stands for SOC, and 5 for ﬁfth-

order upwind biased approximations. The last two numbers denote the order of

approximation of the divergence and gradient operator used to construct the pres-

sure equation Laplacian: 22 refers to SOC approximations whereas 44 denotes

fourth-order central approximations. The high-order methods are accompanied by

sixth-order central interpolation operators and sixth-order central treatment of the

diffusionterms.The 5

44 formulation does not satisfy the integrability constraint

in the inhomogeneous wall normal direction. Only the 2

22 scheme is globally

energy conserving.

The channel computational domain extends from 0 to 4π in x, −1to1iny,

and0to2π in z, and calculations are performed with grids of 64 × 64 × 64 and

128×96×128.Asemi-implicitformulationisusedtoobtaintheintermediateveloc-

ity ﬁeld. The pressure equation is solved by using 2-D FFTs in the homogeneous

x-andz-directionswithalineinversioninthey orinhomogeneousdirectionforeach

combinationofwavenumbers.A nondimensionaltimestepoft =2.5×10

−3

and

1.0×10

−3

is used for the coarse and ﬁne grid simulations, respectively. Velocity

ﬁelds from previous simulations are used as initial conditions and each case is run

for 10 nondimensional time units before any statistics are collected. The statis-

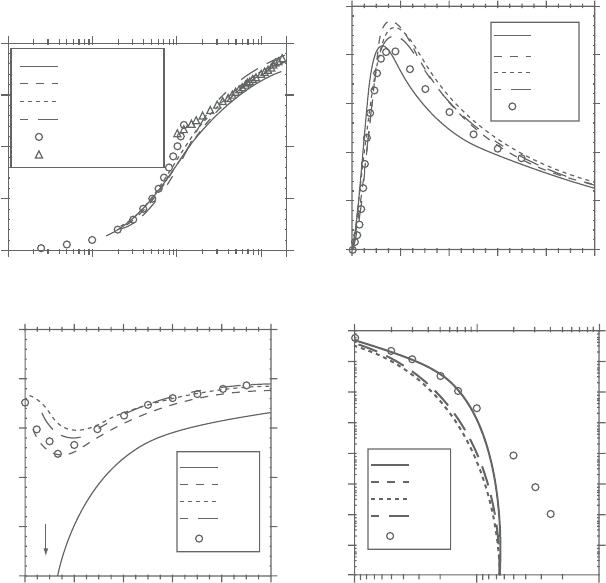
tics are collected for additional 10 nondimensional time units. Figures 6.7 and 6.8

show some representative results for the coarse grid and ﬁne grid simulations,

respectively. The predicted mean streamwise velocity proﬁles in wall coordinates

are compared to the theoretical laminar sublayer proﬁle (u

) and the log-

law proﬁle of u

=2.5ln(y

)+5.5, together with predictions of kinetic energy

Sunden CH006.tex 10/9/2010 15: 39 Page 242

242 Computational Fluid Dynamics and Heat Transfer

(a) (b)

⊥

= y

⊥

=2.5In(y

⊥

)+5.5

0.1 1 10 100

0 20 40 60 80 100

KMM

0.5

−0.5

−1

−1.5

−2.6

s(v)

0 20 40 60 80 100

KMM

0.1

0.01

0.001

0.0001

−5

−6

−7

−8

10 100

KMM

Figure 6.7. Comparisonofdifferentconvectionandpressureformulationsinturbu-

lentchannel ﬂowatRe

=180ataresolutionof64

. (a)Meanvelocity

in wall coordinates; (b) turbulent kinetic energy distribution; (c) one-

dimensional streamwise velocity power spectrum in z-direction; and

(d) skewness of cross-stream velocity ﬂuctuations.

distribution in wall coordinates, 1-D energy spectrum of the streamwise velocity

)aty

=5.6,andthird-ordermomentorskewnessofthecross-streamvelocity,

whichisverysensitivetothe numericalapproximation.Thefollowingobservations

can be made:

1. In both the coarse grid and the ﬁne grid simulation the 2

22 formulation com-

putesthespectrumE

withthebestaccuracy.Thehigh-orderschemes5

and5

both exhibit adissipativebehavior in representingthe spectrum.Thedissipative

nature of the 5

and 5

formulations is also evidenced by the overprediction of

thecorevelocityandtheoverpredictionandright-shiftofthemaximumturbulent

kinetic energy proﬁles for the coarse grid simulations.

Sunden CH006.tex 10/9/2010 15: 39 Page 243

Time-accurate techniques for turbulent heat transfer analysis 243

0 20 40 60 80 100

0.0001

0.001

0.01

0.1

−8

−7

−6

−5

KMM

110

(a) (b)

100

KMM

Figure 6.8. Comparison of different convection and pressure formulations in tur-

bulent channel ﬂow at Re

=180 at a resolution of 128×96×128.

(a) Turbulent kinetic energy distribution and (b) one-dimensional

streamwise velocity power spectrum in z-direction.

2. There are very small differences observed in the prediction capability of 5

and5

22,inspiteoftheformernotsatisfyingtheintegrabilityconstraint(equa-

tions(48)and(49)).Allofthempredictthethirdmomentorskewnesswithmuch

better ﬁdelity than the second-order scheme.

3. As the grid resolution increases to 128×96×128, the high-order upwind

schemes exhibit better accuracy in predicting the turbulent kinetic energy dis-

tribution compared to the 2

22 formulation. However, the 2

22 formulation is

better at predicting the spectral energy distribution.

Itcanbesurmisedfromtheseresultsthathigh-orderupwindschemesinspiteof

their dissipative nature are still very usable and at high resolution in the DNS limit

give more accurate results of turbulent statistics than the SOC difference scheme.

However, they are computationally expensive because of the larger directionally

dependent ﬁnite-difference stencils.

In complex CFD problems with complex grids, there is often the temptation to

use low-order schemes such as second-order upwinding or the third-order upwind

biasedapproximation(QUICK)orothermonotonicitypreservingschemesbecause

of their relative stability and lower computational cost. While these schemes are

useful in steady RANS calculations, they can lead to erroneous results in LES and

DES.To elucidate on this, anormalized variable diagram (NVD) (Leonard [27]) is

used to construct the total variation diminishing (TVD) schemes below. The NVD

is constructed by deﬁning the upstream and downstream directions based on the

cell face ﬂux direction as in Figure 6.9.

Then the normalized variable at any point is deﬁned as:

φ =

φ − φ

− φ

Sunden CH006.tex 10/9/2010 15: 39 Page 244

244 Computational Fluid Dynamics and Heat Transfer

CV CV

Figure 6.9. Nomenclature used to construct the NVD.

−0.5

−1

−0.5

0.5

1.5

0.5 1 1.5

∼

= φ

∼

= 0.5(1+φ

)

∼

= 2φ

∼∼

∼

Second-order central

difference with TVD limiter

−0.5

−1

−0.5

0.5

1.5

0.5 1 1.5

φc

∼

φf = φc

∼∼

= 3/8 + 3/4φ

)

∼

= 2φ

∼∼

∼

= 1

Third order upwind-biased

with TVD limiter

Figure 6.10. NVD diagram forTVD-limited second-order central scheme and the

QUICK scheme.

where

∼

denotes the normalized variable. For example, an SOC difference approx-

imation at the cell face at time step ntφ

=(φ

+ φ

)/2 is written in NVD

coordinates as

=(1+

)/2. The equivalent TVD limiter in NVD coordinates

is given by:

for

≤ 0 and

≥ 1

≤

≤ min[2

,1] for 0 ≤

≤ 1

(57)

Effectively, the ﬁrst condition uses a ﬁrst-order upwind approximation if φ

is not

bounded by φ

and φ

. Within the bounds established in the ﬁrst condition, the

second condition further limits the face value to lie between between φ

and the

minimum of φ

and φ

+ (φ

− φ

). The limiter applied together with the SOC

scheme is illustrated in Figure 6.10 on the NVD. Similarly, the QUICK scheme in

normalized coordinates is expressed as

=3/8+3/4

Incontrast totheTVDlimiter, which isappliedtotheconvected variableatnt

and hence can be too restrictive, Thuburn [28] developed a multidimensional ﬂux

limiterbasedonthelessrestrictiveuniversallimiter(UL)proposedbyLeonard[27].

Sunden CH006.tex 10/9/2010 15: 39 Page 245

Time-accurate techniques for turbulent heat transfer analysis 245

0.1

theoretical

SOC

SOC + TVD

SOC + DSM

SOC + UL

QUICK

(a) (b)

(c)

100

50 100 150 200

DNS (KMN)

SOC

SOC + TVD

SOC + UL

SOC + DSM

QUICK

−6

110

100

−5

0.0001

0.001

0.01

0.1

SOC

DMS(KMM)

SOC + TVD

SOC + DSM

SOC + UL

QUICK

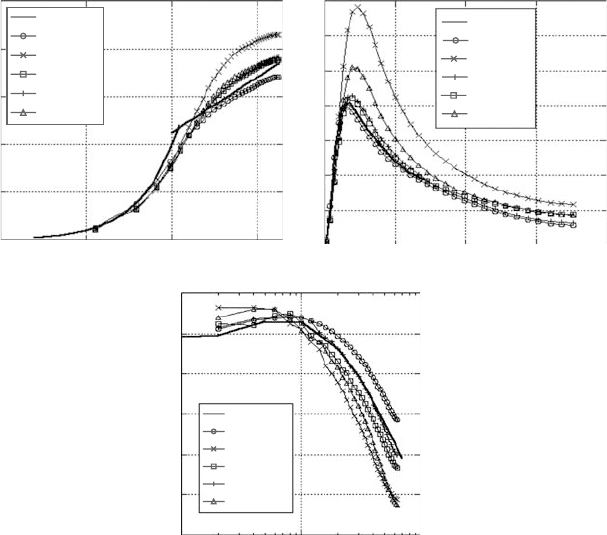
Figure 6.11. Prediction capability of different convective schemes in turbu-

lent channel ﬂow at Re

=180. (a) Mean velocity proﬁle in

wall coordinates; (b) turbulent kinetic energy distribution; and

z-direction.

Inthis scheme,the intermediate velocities areﬁrstcalculated withthebaseapprox-

imations and then checked for monotonicity in a multidimensional framework.

By not applying the monotonicity preserving criteria at time level n, the univer-

sal limiter is much less restrictive than the TVD limiter. The effect of different

schemesistestedinturbulentchannelﬂowatRe

=180withstreamwisegridspac-

ing x

=35.34, spanwise z

=8.84, and cross-stream 0.63≤y

≤ 8.11 for

a domain of 4π × π × 2inx, z and y, respectively and plotted in Figure 6.11.

The resultsare compared withDNS dataofKMM. Infully developedchannel ﬂow

since the ﬂow velocity adjusts to the constant pressure gradient in reaction to the

simulated wall friction, core velocities larger than theory are indicative of a dissi-

pative scheme.This is also typically accompanied byhighturbulent kinetic energy

with the maximum shifted toward the core of the channel. The energy spectrum

also provides additional evidence of the spectral properties of the scheme. Based