Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics
Подождите немного. Документ загружается.

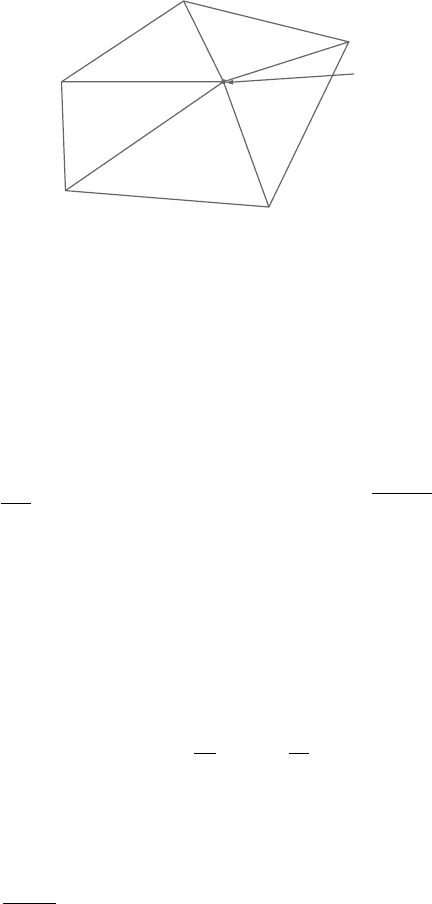
Sunden CH004.tex 10/9/2010 15: 9 Page 156
156 Computational Fluid Dynamics and Heat Transfer
A
3
l
3
l
2
l
1
l
4
l
5
Node
A
2
A
1
A
4
A
5
Figure 4.30. Two-dimensional linear triangular element.
as the Navier–Stokes equations, the derivation of the stability limit is not straight-
forward. A detailed discussion on stability criteria is not given here and readers
are asked to refer to the relevant text books and papers for details (Hirsch [22],
Zienkiewicz and Codina [23]). A stability analysis will give some idea about the
time-steprestrictionsofanynumericalscheme.Ingeneral, forfluiddynamicsprob-
lems, the time-step magnitude is controlled by two wave speeds. The first one is
due to the convection velocity and the second due to the real diffusion introduced
by the equations. In the case of a convection–diffusion equation, the convection
velocity is
√
u
i
u
i
, whichis, intwo dimensionalproblems,
u
2
1
+u
2
2
=|u|.The dif-
fusion velocityis 2k/h where h is thelocalelement size.The time-step restrictions
are calculated as the ratio of the local element size and the local wave speed. It is
therefore correct to write that the time step is calculated as:
t = min(t
c
,t
d
) (68)
where t
c
and t
d
are the convection and diffusion time-step limits, respectively,
which are:
t
c
=
h
|u|
, t
d
=
h
2
2k
(69)
Often, it may be necessary to multiply the time-step t by a safety factor due
to different methods of element size calculations. A simple procedure to calculate
the element size in two dimensions is:
h = min
2Area
i
l
i
, i = 1, number of elements connected to the node (70)
whereArea
i
are thearea of theelements connected tothe node and l
i
are thelength
oftheopposite sidesas showninFigure4.30. Forthenode shownin thisfigure,the
local element size is calculated as:
h = min(A
1
/l
1
,A
2
/l
2
,A
3
/l
3
,A
4
/l
4
,A
5
/l
5
) (71)

Sunden CH004.tex 10/9/2010 15: 9 Page 157
Applications of finite element method to heat convection problems 157
In three dimensions, theterm 2Area
i
is replaced by 3Volume
i
and l
i
is replaced
by the area opposite the node in question.
4.2.6 Characteristic-based split scheme
It is essential to understand the characteristic Galerkin procedure, discussed in
Section 2.4 for the convection–diffusion equation, in order to apply the concept to
solve the real convection equations. Unlike the convection–diffusion equation, the
momentumequation, whichis partof aset ofheat convectionequations, isa vector
equation. A direct extension of the CG scheme to solve the momentum equation
is difficult. In order to apply the CG approach to the momentum equations, we
havetointroduce two steps.In the firststep, the pressureterm fromthe momentum
equation will be dropped and an intermediate velocity field will be calculated.
In the second step, the intermediate velocities will be corrected. This two-step
procedure for the treatment of the momentum equations has two advantages. The
firstadvantageisthatwithoutthepressureterms,eachcomponentofthemomentum
equationissimilartothatof aconvection–diffusionequation andtheCGprocedure
can be readily applied. The second advantage is that removing the pressure term
from the momentum equations enhances the pressure stability and allows the use
of arbitrary interpolation functions for both velocity and pressure. In other words,
the well-known Babuska–Brezzi condition is satisfied (Babuska [24], Brezzi and
Fortin[25], Chung[26]).Owingtothesplitintroducedintheequations,themethod
is referred to as the CBS scheme.
The CG procedure may be applied to the individual momentum components
without removing the pressure term, provided the pressure term is treated as a
source term. However, such a procedure will lose the advantages mentioned in
thepreviousparagraph. Formore mathematicaldetails, pleaserefer toZienkiewicz
etal.[20],ZienkiewiczandCodina[23],Nithiarasu[27]andZienkiewiczetal.[28].
InordertoapplytheCGprocedure,wecanrefertothegeneralcaseofgoverning
generalized porous medium flow and heat transfer equations in non-dimensional
form and indicial notation, for mixed convection, that have been presented in
Section 1.3 (see equations (24)–(26)).
From the governing equations, it is obvious that the application of the CG
schemeisnotstraightforward. However, byimplementingthefollowingprocedure,
it is possible to obtain a solution to the convection heat transfer porous medium
equations.The solution of the free fluid flow equations is obtained by applying the
same procedure.
Temporal discretization
For thesake of simplicity, the asterisks areomitted and the Darcy and Forchheimer
terms in equation (25) are grouped as a “porous” term to obtain:
P =
1
ReDa
+
F
√
Da
|u|
(72)

Sunden CH004.tex 10/9/2010 15: 9 Page 158
158 Computational Fluid Dynamics and Heat Transfer
Temporal discretization along the characteristics of continuity, momentum and
energy conservation equations results in the following set of equations:
∂u
n+ϑ
1
i
∂x
i
= 0 (73)
u
n+1
i
(1 +tεPϑ
3
) −u
n
i
(1 −tεP(1 − ϑ
3
))
=−εt
ϑ
2
∂p
n+1
f
∂x
i
+
(
1 −ϑ
2
)
∂p
n
f
∂x
i
−
t
ε
u
j
∂u
i
∂x
j
n
+
t
J
Re
∂
2
u
i
∂x
2
i
n
+ε
t
2
2
1
ε
2
u
k
∂
∂x
k
u
j
∂u
i
∂x
j
+ u
k
∂
∂x
k
∂p
f
∂x
i
n
+ εt
Ra
PrRe
2
T
n
γ
i
(74)
T
n+1
− T
n
t
=−
u
i
∂T
∂x
i
n
+
1
σRePr
∂
2
T
∂x
2
i
n
+
t
2σ
u
k
∂
∂x
k
u
i
∂T
∂x
i
n
(75)
In equations (74) and (75), additional stabilization terms appear naturally from
thediscretization alongthe characteristics(Zienkiewiczet al.[20]), whilethe char-
acteristic parameters ϑ
1
, ϑ
2
and ϑ
3
(0.5≤ϑ
1
≤1 and 0≤ϑ
i
≤1, with i =2, 3) are
defined according to the following:
∂u
n+ϑ
1
i
∂x
i
= ϑ
1
∂u
n+1
i
∂x
i
+ (1− ϑ
1
)
∂u
n
i
∂x
i
,
∂p
n+ϑ
2
f
∂x
i
= ϑ
2
∂p
n+1
f
∂x
i
+ (1− ϑ
2
)
∂p
n
f
∂x
i
, (76)
[Pu
i
]
n+ϑ
3
= ϑ
3
[Pu
i
]
n+1
+ (1− ϑ
3
)[Pu
i
]
n
.
Different versions of the CBS scheme can be obtained depending on the value
of the above parameters. In particular an SI and anAC version of the CBS scheme
canbeobtained byvaryingthe parameterϑ
2
.Forϑ
2
between0.5 and1,theSI-CBS
is obtained, while for ϑ
2
equal to 0, theAC-CBS scheme is derived. Moreover, for
ϑ
3
between 0.5 and 1, an implicit treatment for the porous term is obtained, while
for ϑ
3
equal to 0, an explicit one is derived.
The splitting in the CBS scheme consists of solving the above equations in a
number of subsequent steps. In the first step, the pressure term is removed from
equation (74) and the intermediate velocity components ˜u
i
are obtained from:
Step 1: Intermediate velocity calculation
˜u
i
(1 +tεPϑ
3
) −u
n
i
(1 +tεP
(
ϑ
3
− 1
)
) =−
t
ε
u
j
∂u
i
∂x
j
n
+
t
J
Re
∂
2
u
i
∂x
2
i
n
+ε
t
2
2
1
ε
2
u
k
∂
∂x
k
u
j
∂u
i
∂x
j
n
+ εt
Ra
PrRe
2
T
n
γ
i
(77)
Sunden CH004.tex 10/9/2010 15: 9 Page 159
Applications of finite element method to heat convection problems 159
Removingthepressuretermfromthemomentumequation,thepressurestability
is enhanced and the use of arbitrary interpolation functions for both velocity and
pressure is allowed. In other words, the well-known Babuska–Brezzi condition is
satisfied(Babuska [24], Brezziand Fortin[25], Chung [26]).The correct velocities
can be determined, once the pressure field is known, using the equation:
Step 3:Velocity correction
u
n+1
i
−˜u
i
=−
1
1
εt
+ Pϑ
3
ϑ
2
∂p
n+1
f
∂x
i
+ (1− ϑ
2
)
∂p
it
art
∂x
i
+
t
2
u
k
∂
∂x
k
∂p
f
∂x
i
n
(78)
The solution of equation (78) is the third step of the algorithm.
Thesecondstepconsistsinthepressurecalculationthroughthecontinuityequa-
tion. This second step is where the SI and AC versions of the scheme differ. In
particular, this second step is obtained in the SI version of the scheme by deriving
equation(78)withrespecttox
i
andimposingequation(73), obtainingthefollowing
Poisson type of equation:
Step 2 SI-CBS: Pressure calculation
0 =−t
1
ε
ϑ
1
∂˜u
i
∂x
i
+ (1− ϑ
1
)
∂u
n
i
∂x
i
+ t
2
∂
2
p
n+1
f
∂x
2
i
(79)
Therefore, in this case, the incompressibility constraint is satisfied at each iter-
ation, and the pressure, evaluated through equation (79), represents the actual
pressure. However, thesolution of equation (79)needsa matrix inversion. Further-
more, the SI version of the scheme uses a global time step, which is the minimum
value of the time step limit over the entire domain.
Alternatively, the AC scheme can be derived when the left hand side of equa-
tion (79) is obtained from a mass conservation equation retaining the transient
density term:
∂ρ
f
∂t
+
1
ε
∂(ρ
f
u
i
)
∂x
i
= 0 (80)
In general, it is possible to relate the density time variation to the pressure time
variation, through the speed of sound, as follows:
∂ρ
f
∂t
=
1
c
2
∂p
f
∂t
(81)
wheretherealcompressibilityparameter, c (compressiblewavespeed),approaches
infinity for many incompressible flow problems and the solution scheme becomes
stiff and imposes severe time step restrictions. However, this parameter can be
replaced locally by an appropriate artificial value, β, of finite value, employing the

Sunden CH004.tex 10/9/2010 15: 9 Page 160
160 Computational Fluid Dynamics and Heat Transfer
AC method, that was first introduced by Chorin [29] and then further developed
[30–42]:
∂ρ
f
∂t
=
1
β
2
∂p
art
∂t
⇒
1
β
2
p
it+1
art
− p
it
art
t
=−
ρ
f
ε
∂u
it+ϑ
1
i
∂x
i
(82)
Inequation(82), thepressureisanartificialpressure, becausetheincompressibility
constraintisnotachievedateachtimestep, butonlywhensteady-stateconvergence
is reached. The superscripts it +1 and it are referred to the iterative procedure and
do not refer to real time levels.The second step of theAC scheme is carried out by
imposing the equation (82) as:
Step 2 AC-CBS: Pressure calculation
1
β
2
(p
it+1
art
− p
it
art
) =−t
1
ε
ϑ
1
∂˜u
i
∂x
i
+
(
1 −ϑ
1
)
∂u
it
i
∂x
i
+ t
2
∂
2
p
it
art
∂x
2
i
(83)
The local value of β is calculated through the following procedure:
β = max(0.5,u
conv
,u
diff
,u
ther
) (84)
Thelocal convective,diffusiveand thermal velocities canbecalculated through
the following non-dimensional relations:
u
conv
=
√
u
i
u
i
, u
diff
=
2
hRe
,u
ther
=
2
hRePr
. (85)
Thediffusive timestep limitationfor theAC methodmay bewritten ash
2
/Re/2,
while the convective time step limitation may be written as:
t
conv
=
h
|u|+β
(86)
The above relation includes the viscous effect via the artificial parameter.
Depending on the problem of interest, it is possible to consider other equations
coupled totheabove set, suchasspecies concentration for multi-componentflows.
Thefourthstep, for non-isothermal problems, is representedbythe energy con-
servationequation(75)thatallowscalculatingthetemperatureateveryiterationfor
problems with a coupling between momentum and energy conservation equations
occurs.
Spatial discretization and solution methodology
The spatial discretization of the governing equations is obtained through Galerkin
finite element procedure and triangularelements. Within an element, each variable
is calculated through linear approximation on the basis of nodal values, according
to the following equation:
φ =
3
n=1
N
n
φ
n
(87)

Sunden CH004.tex 10/9/2010 15: 9 Page 161
Applications of finite element method to heat convection problems 161
whereN
n
is the shape function atnoden and φ
n
is the value of the generic variable
φ at node n. Applying the standard Galerkin procedure to the set of equations
presented in the previous section, the following four steps, expressed in a matrix
form, are obtained:
Step 1: Intermediate velocity calculation
M˜u
i
= (1 − tεP)Mu
n
i
−
t
ε
[Cu
i
]
n
− t
J
Re
[K
d
u
i
]
n
−
1
2
t
2
ε
[K
u
u
i
]
n
(88)
+εt
Ra
PrRe
2
MTγ
i
n
+ t
J
Re
[f
d
]
n
+
1
2
t
2
ε
[f
u
]
n
Step 2 SI-CBS: Pressure calculation
[K
p
p
f
]
n+1
=−
1
εt
[D˜u
i
] (89)
Step 2 AC-CBS: Pressure calculation
1
β
2
M(p
it+1
art
− p
it
art
) =−
t
ε
[D˜u
i
] −t
2
[K
p
p
art
]
it
(90)
Step 3:Velocity correction
M(u
n+1
i
−˜u
i
) =−εt
ϑ
2
Dp
n+1
f
+ (1− ϑ
2
)Dp
it
art
−
t
2
K
u
p
n
f
(91)
Step 4: Temperature calculation
MT
n+1
= MT
n
− t[CT]
n
−
tλ
RePrR
k
[K
d
T]
n
(92)
−
t
2
2R
k
[K
u
T]
n
+
tλ
RePrR
k
[f
t
]
n
+
t
2
2R
k
[f
ut
]
n
whereM isthe mass matrix,C istheconvectionmatrix, K
d
isthediffusionmatrix,
K
u
is the stabilization matrix obtained from higher-order terms, f
d
and f
u
are the
boundary vectorsfromthemomentumequation, K
p
isthe stiffness matrix, Dis the
gradient matrix, f
t
and f
ut
aretheboundary vectorsfrom thetemperature equation.
Details of all the terms presented in equations (88)–(92) are given in Lewis et al.
[19] and Zienkiewicz et al. [20].
In the present procedure, the mass matrix is lumped using a standard row-
summing approach, inverted and stored in an array during the pre-processing.
Therefore, in theAC formulation, the calculation of the artificial pressure at it +1
iteration, through equation (90), does not need a matrix inversion and the result is
a matrix inversion-free procedure. On the other hand, in the second step of the SI
solution procedure, the stiffness matrix needs to be inverted at each iteration.

Sunden CH004.tex 10/9/2010 15: 9 Page 162
162 Computational Fluid Dynamics and Heat Transfer
u = 0, v = 0, q = 1
u = 0, v = 0, q = 1
u = 1
T = 0
y
x
(b)
(a)
Figure 4.31. Forcedconvectioninaporouschannel.(a)Computationaldomainand
boundary condition; (b) structured computational grid (3,321 nodes,
6,400 elements).
Some examples
Boththeschemespresentedabovecanbeusedtosolvemanyengineeringproblems,
such as mixed, natural or forced convection both in fluid-saturated porous media
and in partly porous domains, or simply in free fluid flow cases.
As mentioned before, changing the properties such as porosity and thus per-
meability, it is possible to handle porous medium-free fluid interface problems as
a single problem with different properties. The following limits are used for the
porous medium part and for the free fluid part:
ε<1
Da = finite
⇒ porous medium
ε = 1
Da →∞
⇒ free fluid (93)
A suitable set of matching conditions, to connect the porous medium and the
free fluid domains, is needed (Massarotti et al. [43]).
The firstexampleisthe forcedconvection heattransferinside auniform porous
channel with constant wall heat flux.The computational domain, together with the
boundary conditions employed, is sketched in Figure 4.31a, while Figure 4.31b
shows the computational grid employed.The flow enters the domain from the left
with a constant velocity and at a non-dimensional temperature T =0.The channel
walls are heated by a constant heat flux. The numerical results have been obtained
using a non-uniform grid with 6,400 elements and 3,321 nodes.
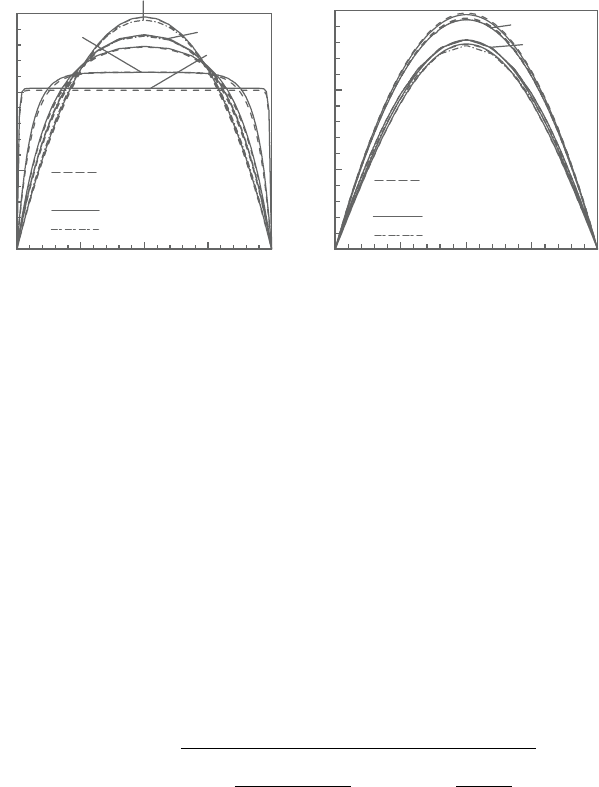
Figure 4.32 shows the non-dimensional velocity and temperature profiles, for
different Darcy numbers, varying from 10
−4
to 1.0 at a section, where the flow
and the thermal field are hydrodynamically and thermally developed. The results
havebeen comparedwiththe analytical solutionspresented by Nieldet al. [44]and
Lauriat and Vafai [45]. The dimensionless temperature is evaluated using:
T
mix
=
1
u
mean
S
x
&
S
x
u
i
T
i
dS (94)
Sunden CH004.tex 10/9/2010 15: 9 Page 163
Applications of finite element method to heat convection problems 163
y
u /u
mean
−1 −0.5 0
(a) (b)
0.5 1
0
0.5
1
1.5
Analytical Nield
et al. [44]
AC-CBS
SI-CBS
Da = 10
−4
Da = 10
−2
Da = 5x10
−2
Da =10
−1
Da = 1
y
TT
wall
/T
mix
T
wall
−1 −0.5 0 0.5 1
0
0.5
1
1.5
Analytical Lauriat
and Vafai [45]
AC-CBS
SI-CBS
Da = 10
−3
Da = 10
−1
Da = 1
Da = 10
−4
Figure 4.32. Forced convection in a porous channel: (a) non-dimensional velocity
as function of transverse distance; (b) non-dimensional temperature
as function of transverse distance.
where u
mean
is the mean velocity in the section considered S
x
.
For a small Darcy number (10
−4
), the velocity profile is nearly independent of
the transverse distance and slip flow occurs at the walls (Figure 4.32). An increase
in Darcy number leads to a non-linear distribution of the velocity.When the Darcy
number is equal to unity, the velocity profile approaches a profile similar to that of
free fluid flow.
The non-dimensional temperature increases as the Darcy number decreases, as
shown in Figure 4.32. A decrease in the Darcy number corresponds to a decrease
in the fluid velocity in the middle of the channel and therefore the conduction heat
transfer is dominating over the effect of convection.
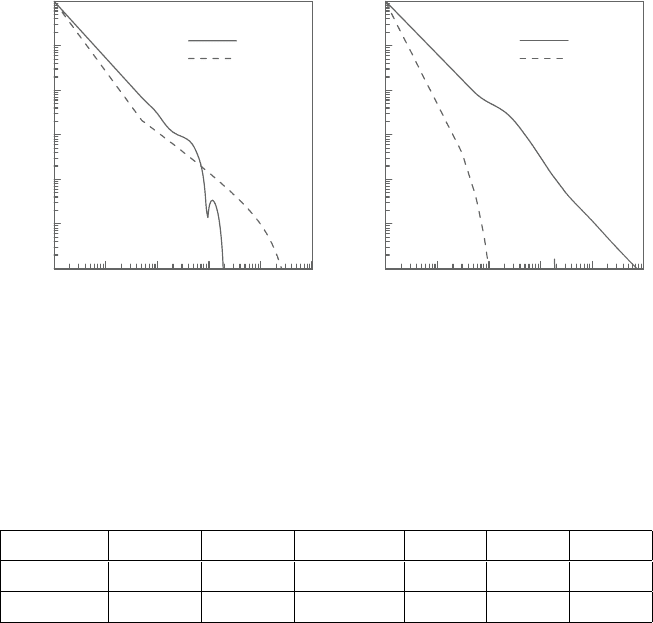
Figure4.33shows theconvergence historiestosteady statefortheAC-CBSand
SI-CBS schemes obtained by using the following L
2
norm for velocities:
Velocity residual =
+
,
,
-
nodes
i=1
|u
i
|
n+1
−|u
i
|
n
t
i
2
.
nodes
i=1
|u
i
|
n+1
t
i
2
(95)
ThisfigureshowsthattheSIversionoftheschemeconvergesfasterastheDarcy
numberdecreases.Instead,theACversionoftheschemehasanoppositebehaviour.
Table 4.1reports the CPUtime needed by both the proceduresto reach steady state
solution, on a machine with 4Gb of RAM and 2.4GHz CPU speed. These results
confirm the behaviour shown in Figure 4.33. In particular, Table 4.1 shows that
theAC-CBSschemeconvergesfasterthanthe SI-CBS scheme when Da≥10
−2
.It
wasnoticedthattheSI-CBSschemeneedsmore timethantheAC-CBSschemeper
time iteration. In correspondence of smaller Darcy numbers (Da≤10
−3
), the AC-
CBS scheme takes more time to reach the steady state. This is due to the time step
Sunden CH004.tex 10/9/2010 15: 9 Page 164
164 Computational Fluid Dynamics and Heat Transfer
Iterations
Velocity residual
10
0
10
0
10
1
10
2
10
3
10
4
10
5
10
−1
10
−2
10
−3
10
−4
10
−5
10
−6
AC-CBS
SI-CBS
(a)
Iterations
Velocity residual
10
0
10
0
10
1
10
2
10
3
10
4
10
5
10
−1
10
−2
10
−3
10
−4
10
−5
10
−6
AC-CBS
SI-CBS
(b)
Figure 4.33. Convergence histories for SI and AC scheme. (a) Da=1;
(b) Da=10
−4
.
Table 4.1. CPUtime(s)forforcedconvectioninaporouschannelatdifferentDarcy
numbers
Da 1 10
−1
5×10
−2
10
−2
10
−3
10
−4
AC-CBS 35 87 137 491 4,341 6,400
SI-CBS 14,730 10,250 8,055 3,357 1,107 250
calculationprocedureused.Essentially, theACschemebecomesslowerinreaching
the steady state when diffusion is overriding the effect of convection (Da≤10
−3
)
and the local time step approaches the global time step, losing the advantage of
using a higher time step in the convective zones.
Thesecond exampleisthe naturalconvection inacavityheated uniformlyfrom
thebottom side.Thecomputational domain,togetherwith theboundaryconditions
employed, issketchedin Figure 4.34a,whileFigure4.34b showsthecomputational
grid employed, composed of 7,200 triangular elements and 3,721 nodes.
Figure4.35showsthedimensionlesstemperaturecontoursforaPrandtlnumber
equal to 0.71, and for two different Rayleigh numbers (10
6
and 7×10
4
) and two
differentDarcynumbers(10
−3
and10
−4
).Theresultsobtainedhavebeencompared
with the numerical solution presented by Basak et al. [46].
In general, the fluid circulation is strongly dependent on the Darcy number.
In fact, when smaller Rayleigh and Darcy numbers are considered, the flow is
very weak and the temperature distribution is similar to that of stationary fluid
(Figure 4.35a). As the Darcy number increases, the role of convection becomes
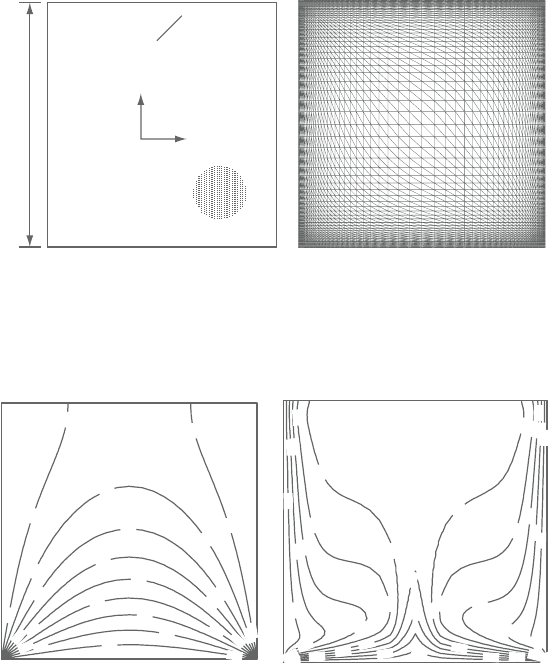
Sunden CH004.tex 10/9/2010 15: 9 Page 165
Applications of finite element method to heat convection problems 165
1
(a) (b)
u=v=0
T=0
u=v=0, T=0
u=v=0
y
x
T=0
u=v=0, =0
∂T
∂y
Figure 4.34. Natural convection in a porous cavity heated from the bottom side:
(a) computational domain and boundary conditions; (b) structured
computational grid (3,721 nodes, 7,200 elements).
0.4
0.1
0.4
0.3
0.1
0.3
0.1
0.1
0.8
0.7
0.5
0.4
0.1
0.3
0.2
0.9
0.8
0.7
0.5
0.4
0.6
0.3
0.1
0.1
0.1
0.4
0.2
0.3
0.5
0.1
0.4
0.3
0.2
0.1
0.4
0.9
0.2
0.2
0.1
0.6
0.7
0.2
0.6
0.5
0.8
0.v
0.6
0.8
0.7
0.2
0.3
0.4
0.5
0.7
0.6
0.4
0.5
0.5
0.5
0.4
0.3
0.3
0.4
0.3
0.9
0.5
0.2
0.2
0.5
0.2
(a) (b)
Figure 4.35. Temperature contoursfornaturalconvectionina porouscavityheated
from the bottom side. (a) Ra=7×10
4
and Da=10
−4
; (b) Ra=10
6
and Da=10
−3
.
more significant and the fluid rises up strongly from the middle portion of the
bottom wall, as depicted in Figure 4.35b.
Figure 4.36 shows the steady-state convergence histories for the AC-CBS and
the SI-CBS schemes.This figure shows a different behaviour from that of the case
of forced convection flow problem. When natural convection occurs, theAC-CBS
schemeconvergesfasterthantheSI-CBSschemeforanyRayleighorDarcynumber,
bothintermsofnumberofiterations(Figure4.36)andCPUtimetoreachthesteady
state (Table 4.2).
The SI-CBS algorithm takes more time to reach the steady state because of the
couplingbetweenmomentumandenergyconservationequations presentinnatural
convection problems. The coupling is due to the presence of a generation term on
