Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics

Подождите немного. Документ загружается.

Sunden CH004.tex 10/9/2010 15: 9 Page 136

136 Computational Fluid Dynamics and Heat Transfer

Figure 4.8. Natural convection in a square cavity. Streamlines and isotherms at

Ra=10

Figure 4.9. Natural convection in a square cavity. Streamlines and isotherms at

Ra=10

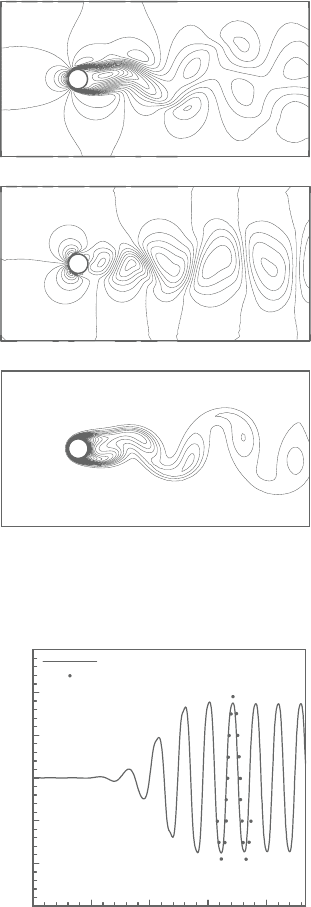
Figure 4.10. Flow past a circular cylinder. Finite element mesh, 7,129 nodes and

13,990 elements.

Sunden CH004.tex 10/9/2010 15: 9 Page 137

Applications of ﬁnite element method to heat convection problems 137

(a)

(b)

(c)

Figure 4.11. Flow past a circular cylinder, Re=100. (a) Horizontal velocity

contours; (b) vertical velocity contours; (c) temperature contours.

Adimensional time

Vertical velocity

0.6

0.4

0.2

0 15304560

−0.2

−0.4

−0.6

AC-CBS

de Sampaio et al. [4]

Figure 4.12. Flow past a circular cylinder. The vertical velocity distribution at an

exit point of the domain with respect to real time. Comparison with

de Sampaio et al. [4].

Sunden CH004.tex 10/9/2010 15: 9 Page 138

138 Computational Fluid Dynamics and Heat Transfer

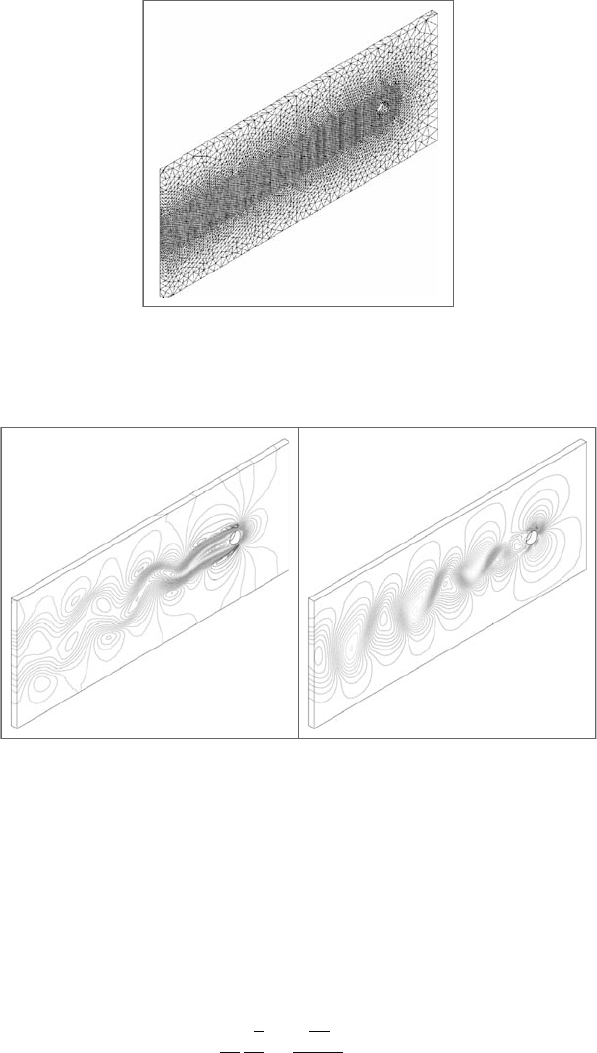
Figure 4.13. Three-dimensional ﬂowpast acircular cylinder.Finiteelementmesh:

17,382 nodes, 69,948 elements.

Figure 4.14. Three-dimensionalﬂowpastacircularcylinder,Re=100; u

velocity

contours (left); u

velocity contours (right).

4.1.2 Non-dimensional form of turbulent ﬂow equations

For turbulent ﬂow computations, Reynolds averaged Navier–Stokes equations of

motion are written in conservation form as follows:

Mean continuity equation

∂p

∂t

∂(

ρu

)

∂x

= 0 (10)

Sunden CH004.tex 10/9/2010 15: 9 Page 139

Applications of ﬁnite element method to heat convection problems 139

Mean momentum equation

∂

∂t

∂

∂x

) =−

∂

∂x

∂τ

∂x

∂τ

∂x

(11)

whereβ isanAC parameter, which will be well explained in Section 2.6,

are the

mean velocity components, p is the pressure, ρ is the density and τ

is the laminar

shear stress tensor given as:



∂

∂x

∂

∂x

−

∂

∂x



(12)

The Reynolds stress tensor, τ

, is introduced by Boussinesq assumption as:



∂

∂x

∂

∂x

−

∂

∂x



−

kδ

(13)

In the above equations, ν is the kinematic viscosity of the ﬂuid, ν

is the turbulent

eddy viscosity and δ

is the Kroneker delta.The following non-dimensional scales

are used to derive the above equations:

∗

ref

∗

ref

∗

ρu

ref

∗

ref

,ε

∗

εL

ref

∗

ref

, ˆv

∗

ref

(14)

where L is a characteristic dimension and the subscript ref indicates a reference

value. The turbulent ﬂow solution is obtained by solving equations (10) and (11)

with appropriate boundary conditions and a turbulence model, as the Spalart–

Allmaras model(Spalart andAllmaras [7], Nithiarasu andLiu [8], Nithiarasu etal.

[9]). The Spalart–Allmaras (SA) model was ﬁrst introduced for aerospace appli-

cations and currently being adopted for incompressible ﬂow calculations. The SA

model is another one-equation model, which employs a single scalar equation and

several constants to model turbulence.The scalar equation is:

∂ˆv

∂t

∂(¯u

ˆv)

∂x

= c

Sˆv +

Reσ



∂

∂x

(1 +ˆv)

∂ˆv

∂x

+ c



∂ˆv

∂x





−



ˆv



(15)

where

S = S +

(ˆv/k

(16)

and

= 1 −X/(1 +Xf

) (17)

Sunden CH004.tex 10/9/2010 15: 9 Page 140

140 Computational Fluid Dynamics and Heat Transfer

In equation (16) S is the magnitude of vorticity. The eddy viscosity is

calculated as:

=ˆvf

(18)

where

= X

/(X

+ c

) (19)

and

X =ˆv/v (20)

The parameter f

is given as:

= g



1 +c

+ c



1/6

(21)

where

g = r + c

− r) (22)

and

r =

ˆv

(23)

The constants are c

=0.1355, σ =2/3, c

=0.622, k =0.41, c

(1+c

)/σ, c

=0.3, c

=2 and c

=7.1. From the above equations it is clear

thattheturbulentkineticenergyisnotcalculatedhere.Thus,thelasttermofequation

(13) is dropped when SA model is employed.

Some examples

Thefollowingresults areobtainedbysolvingtheaboveequationsusinganAC CBS

algorithm and ﬁnite element discretizationtechnique that will be described later in

this chapter.

A standard test case commonly employed for turbulent incompressible ﬂow

models at moderate Reynolds number is the recirculating ﬂow past a backward-

facingstep.ThedeﬁnitionoftheproblemisshowninFigure4.15.Thecharacteristic

dimension of the problem is the step height.All other dimensions are deﬁned with

respect to the characteristic dimension. The step is located at a distance of four

times the step height from the step. The inlet channel height is two times the step

height.Thetotal lengthofthechannelis 40times thestep height.The inletvelocity

proﬁle is obtained from the experimental data reported by Denham et al. [10]. No

slipconditionsapplyonthesolidwalls.Aﬁxedvalueof0.05fortheturbulentscalar

variable of the SA model at inlet was prescribed.The scalar variable was assumed

to be zero on the walls. Both structured and unstructured meshes were employed

in the calculation (Figures 4.16 and 4.17).

Sunden CH004.tex 10/9/2010 15: 9 Page 141

Applications of ﬁnite element method to heat convection problems 141

Parabolic u

and u

= 0

4L 36L

p = 0

= u

= 0

Figure 4.15. Turbulentﬂowpastatwo-dimensionalbackward-facingstep. Problem

deﬁnition.

Figure 4.16. Detail of the structured mesh (8,092 elements and 4,183 nodes) near

the step.

Figure 4.17. Detail of the unstructured mesh (8,662 elements and 4,656 nodes)

near the step.

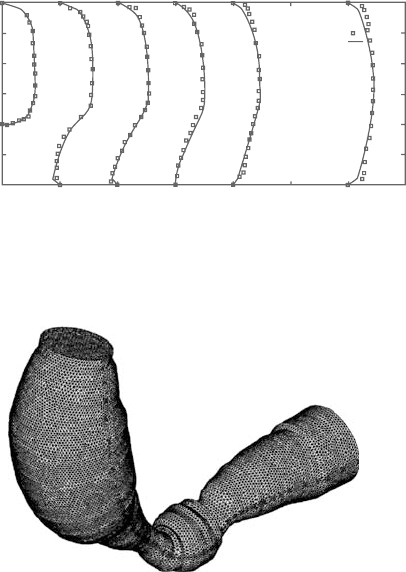
Figure4.18shows the comparison of velocity proﬁles against the experimental

data of Denham et al. [10]. The SA model predicts accurately the recirculation

region.

Theotherturbulenceproblemconsideredisacomplexthree-dimensionalmodel

of ﬂow through an upper human airway (Nithiarasu and Liu [8], Nithiarasu et al.

[9]). The geometry used is a reconstruction of an upper human airway employed

in the spray dynamics studies (Gemci et al. [11]). It is apparent from the available

studies on particle movement in the upper human airways that this problem is

important (Li et al. [9, 10], Martonen et al. [11]). To understand the mechanism

behind many upper human airway-related problems including “sleep apnoea” and

vocal cord-related problems. Most of the reported studies on upper airway ﬂuid

dynamicsuse eitherstructured orsemi-structured meshesinthecalculations.Here,

the results obtained with an unstructured mesh are presented. The surface mesh

of the grid used in the present study is shown in Figure 4.19. This mesh contains

just under a million tetrahedral elements. The mesh is generated using the PSUE

code (Morgan et al. [6]).The Reynolds number of the ﬂow is deﬁned based on the

Sunden CH004.tex 10/9/2010 15: 9 Page 142

142 Computational Fluid Dynamics and Heat Transfer

Exp.

SA model

Re = 3,025

2.5

1.5

Vertical distance

Horizontal velocity

0.5

024 68101214

Figure 4.18. Incompressible turbulent ﬂow past a backward-facing step. Velocity

proﬁles at various downstream sections at Re=3,025.

Figure 4.19. Incompressible turbulent ﬂow through a model upper human airway.

Surface mesh.

diameter of the narrow por tion close to the epiglottis. The total non-dimensional

lengthofthedomaininthehorizontaldirectionis29.68,andintheverticaldirection

it is 23.05.The diameter at the inlet of the geometry (at the top) is 4.91.

A uniform velocity is assumed at the inlet of the geometry in the negative

direction perpendicular to the inlet surface in the downward direction. No slip

conditionsare assumedon thesolidwalls.Theturbulentscalarvariablevalueat the

inlet is ﬁxed at 0.05 and assumed to be equal to zero on the walls.

Figure 4.20 shows the contours of velocity components and pressure within a

section alongthe axisin the middleof thegeometry. It isapparent that themajority

of the activities are taking place near the narrow portion close to the epiglottis of

the upper human airway. The ﬂow is accelerated as it passes through the narrow

portion of the airway. As seen, the pressure contours are clustered close to the

narrow portion representing a very high gradient region. Figure 4.21 shows the

velocityvectorswithinthe section.The velocityvectorsclosetothenarrowportion

are also shown in this ﬁgure. As seen, the recirculation region is clearly predicted

by theAC-CBS method.

Sunden CH004.tex 10/9/2010 15: 9 Page 143

Applications of ﬁnite element method to heat convection problems 143

(a) (b)

(c)

Figure 4.20. Incompressible turbulent ﬂow through a model upper human airway.

(a) u

contours, (b) u

contours, (c) pressure contours.

(a) (b)

Figure 4.21. Incompressible turbulent ﬂow through a model upper human airway.

(a)Velocity vectors and (b) velocity vectors near the narrow portion.

4.1.3 Porous media ﬂow: the generalized model equations

Thegeneralformoftheequationsforaporousmediumcanbederivedbyaveraging

theNavier–Stokesequationsoverarepresentativeelementaryvolume(REV;Figure

4.22),usingthewell-knownvolumeaveragingprocedure(Whitaker[15],Vafaiand

Tien [16], Hsu and Cheng [17]).

Sunden CH004.tex 10/9/2010 15: 9 Page 144

144 Computational Fluid Dynamics and Heat Transfer

Fluid

REV

Figure 4.22. Representative elementary volume.

The non-dimensional form of the generalized model for the description of ﬂow

through a ﬂuid-saturated porous medium can be written as:

Continuity equation

∂u

∗

∂x

∗

= 0 (24)

Momentum equation

∂u

∗

∂t

∗

∂u

∗

∂x

∗

=−

∂p

∗

∂x

∗

εRe

∂

∂x

∗



∂u

∗

∂x

∗



(25)

−

Re Da

∗

−

√

∗

PrRe

∗

Energy equation

∂T

∗

∂t

∗

+ u

∗

∂T

∗

∂x

∗

PrRe

∂

∂x

∗



∂T

∗

∂x

∗



(26)

whereDa is the Darcy number and F is the Forchheimercoefﬁcient.The buoyancy

effects are incorporated by invoking the Boussinesq approximation:

g(ρ

− ρ

ref

) = ρ

ref

gβ(T

ref

− T) (27)

wherethesubscriptfreferstotheﬂuidthatsaturatestheporousmedium.Thescales

and the parameters used to derive the above non-dimensional equations for mixed

convection through a saturated porous medium are the same as those shown at the

beginning of the chapter.The new parameters introduced here are:

J =

eff

,σ =

ε(ρc

)

+ (1− ε)(ρc

)

(ρc

)

,λ

∗

eff

,Da=

(28)

where J istheratiobetweentheeffectiveandtheﬂuidviscosity,σ istheheatcapac-

ityratio,λ*istheratiobetweentheeffectiveandtheﬂuidthermalconductivity,Dais

Sunden CH004.tex 10/9/2010 15: 9 Page 145

Applications of ﬁnite element method to heat convection problems 145

= parab.

= 0

= 1

= 0

= 1

= 0

(a) (b)

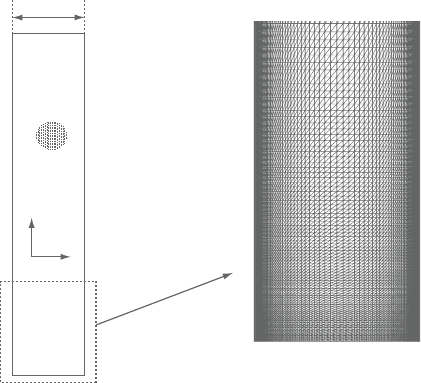
Figure 4.23. Mixed convection in porous vertical channel. (a) Computational

domain and boundary conditions; (b) detail of the structured com-

putational grid near the entrance (8,601 nodes and 16,800 elements).

theDarcynumber, κ andε arethepermeabilityandporosity ofthemedium,respec-

tively, thesubscriptspandeffrefertotheporousmediumandtotheeffectivevalues,

respectively. As mentioned, equations (24)–(26) are derived for mixed convection

problems, therefore this set of PDEs describes both natural and forced convection.

Whenforcedconvectiondominatestheproblem(Ra/PrRe

< 1),thebuoyancyterm

on the right hand side of the momentum conservation can be neglected.

Thegeneralizedmodel equationsintroducedabovereduceto theNavier–Stokes

equations when the solid matrix in the porous medium disappears, that is when

ε →1 and Da→∞, while, as the porosity ε →0 and Da→0, the equations rep-

resent a solid.Therefore, the procedure can be used to describe interface problems

in which a saturated porous medium interacts with a single-phase ﬂuid. In these

cases, it is possible to use a single domain approach, by changing the property of

the medium accordingly.

Some examples

The following results are obtained by solving the above equations for mixed con-

vection ﬂows by using an AC version of the CBS algorithm and ﬁnite element

discretization technique that will be explained later.

The example showed here is the fully developed mixed convection in a region

ﬁlled with a ﬂuid-saturated porous medium, conﬁned between two vertical walls.

Thecomputational domainand theboundaryconditions areshowninFigure4.23a.