Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях

Подождите немного. Документ загружается.

заменяем по третьему измерению однородным слоем и значения коэффициентов для него

определяем как среднее, средневзвешенное и т.д. Попытка внесения в модель учета ряда

факторов, введение третьего измерения приводят к значительному усложнению модели и

езкому повышению размерности задачи. К тому же, в такой усложненной модели

появляются параметры, которые невозможно или крайне трудно измерить. При их задании

опять вводятся некоторые допущения, которые только затрудняют и ухудшают точность

ешения задачи.

Как показывает практика, использование детерминированных моделей с четкими значениями

параметров (даже при наличии адаптационного процесса их уточнения путем решения

обратных задач) приводит к тому, что модель оказывается излишне грубой. Методы

интервального анализа дают возможность построить модель для случая, когда для каждого из

этих коэффициентов задан интервал допустимых значений. Однако на практике в связи с

наличием информации о том, что какие-то значения коэффициентов более допустимы, чем

другие, описание этих коэффициентов в виде нечетких множеств является более удачным. В

этом случае на интервале дополнительно задается функция принадлежности, причем, если

информация о различии допустимости имеет статистический характер, то эта функция может

быть определена объективно, если нет — то субъективно, на основе приближенного

отражения экспертом в агрегированном виде имеющегося у него неформализованного

представления о величине этого коэффициента.

Естественно, что введение нечетких коэффициентов усложняет процесс моделирования,

однако в этом случае решение становится адекватным принятым упрощениям, например, при

исключении третьей координаты z понятие в точке (х, у) становится размытым, нечетким, так

как относится не к точке, а к интервалу.

В общем случае динамику дискретных систем можно представить уравнением состояния

[166]:

где

- пространство состояний,

- множество допустимых управлений ,

- переходная

функция состояния, в общем случае нелинейная

Эта система является детерминированной, если в любой момент времени k можно однозначно

определить ее новое состояние в момент времени (k+1) по текущему состоянию и

управлению .

Для стохастических систем переходная функция записывается в виде

где

- множество распределений вероятности на

. Для учета неопределенностей в модель

могут вводится случайные величины или коэффициенты. Однако для этих моделей

необходимо иметь информацию для построения вероятностных распределений.

Неполностью оп

еделенные п

оцессы можно модели

овать с помощью аппа

ата нечетких

множеств. Коэффициенты и некоторые величины могут быть заданы в виде функций

принадлежности. Тогда динамика системы описывается нечетким отношением

, (6.83)

представляющим собой нечеткое подмножество декартова произведения .

Величина рассматривается как интенсивность перехода или, точнее, как

степень принадлежности элемента образу пары при отображении F, т.е.

основной характеристикой системы является функция принадлежности .

Используя понятие нечеткого отношения, можно ввести следующие пути определения

функции F:

1. Если отсутствует модель процесса и имеется лишь лингвистическое описание желаемого

поведения системы вида "если давление газа очень большое, то значительно увеличить

асход". Подобные выражения дают информацию о том, что должно произойти в системе при

поступлении на ее вход управляющих воздействий в форме нечетких множеств,

определенных на универсальных множествах "давление газа" и "расход". Тогда нечеткое

условное высказывание есть нечеткое отношение, которое определяется как

;

; .

Если F будет являться нечеткой функцией, то состояние нечеткой системы в момент времени

(k+1) есть условное по и нечеткое множество, характеризуемое функцией

принадлежности .

2. Возможно использование имеющейся модели системы для задания функции F. Рассмотрим

вначале случай свободной динамики системы и построим рекуррентную процедуру оценки

состояния динамической системы в нечетких условиях.

В настоящее время для оценивания состояния динамических систем в теории оптимального

оценивания широкое распространение

получил байесовский подход. Однако достаточно

приемлемые для практической реализации результаты получены лишь для случая линейных

динамических систем с гауссовскими помехами. Для таких систем оценка состояния может

быть проведена с использованием рекуррентного фильтра Калмана [67].

Рассматривались также методы, использующие фильтры Калмана для нелинейных

относительно состояния систем и негауссовских помех [41]. При этом проводится

предварительная

линеаризация нелинейных уравнений объекта и канала наблюдений,

негауссовские помехи приближенно аппроксимируются гауссовскими, что приводит

ухудшению точности результатов.

На практике ситуация также усложняется частичным или полным отсутствием информации о

статистических характеристиках шумов. Поэтому авторами предлагается для решения задачи

оценивания применять теорию нечетких множеств.

Рассмот

им нелинейн

ю динамическ

ю систем

с диск

етным в

еменем:

, (6.84)

для которой измерение и состояние системы связаны соотношением:

. (6.85)

В этих уравнениях индекс k соответствует k-му моменту времени;

- нелинейные функции соответствующих аргументов;

- состояние динамической системы,

- нечеткая помеха, заданная для каждого момента времени k функцией принадлежности

;

- ошибка измерения с известной функцией принадлежности ;

Предполагается известной и функция принадлежности для начального состояния .

В процессе функционирования системы в общем случае носитель начального нечеткого

состояния расширяется. Чтобы уменьшить неопределенность ситуаций при принятии

ешений, необходимо использовать дополнительную информацию о замерах и исследованиях

в системе.

Будем предполагать независимость ошибок измерения, помех и состояния в смысле

определения независимости нечетких величин. При заданной условной функции

принадлежности состояния при наличии последовательности измерений

наилучшая четкая оценка состояния в момент времени k может быть

найдена из соотношения:

При наличии известной условной функции принадлежности оптимальная

точечная оценка состояния системы в момент (k+1) может быть определена аналогично:

Поскольку для реальных процессов функции и являются

унимодальными, то процедура нахождения максимума довольно проста. Для оценивания

состояний выведем рекуррентную процедуру для функции принадлежности . На

основании определения условной функции принадлежности можно записать, что

(

6.86

)

где вектор представлен в виде .

Используя определение (6.86) и уравнение для ошибки измерения получаем:

а из условия независимости , , следует, что

. (6.87)

Условную функцию принадлежности можно определить на основе уравнения

динамики системы с использованием определения условной функции принадлежности:

(6.88)

Используя определение операции проектирования и учитывая соотношение (6.84), уравнение

(6.88) может быть записано в виде

Используя в качестве характеристики нечеткого начального состояния априорную

функцию принадлежности можно определить функцию , принимая во

внимание (6.85):

. (6.89)

Окончательно рекуррентные соотношения для нахождения апостериорной функции

принадлежности для нечеткого состояния системы на любом шаге (k+1) с учетом (6.89)

можно записать:

; (6.90)

. (6.91)

Для сл

чая

становившегося состояния использ

ется только вы

ажение

(

6.90

)

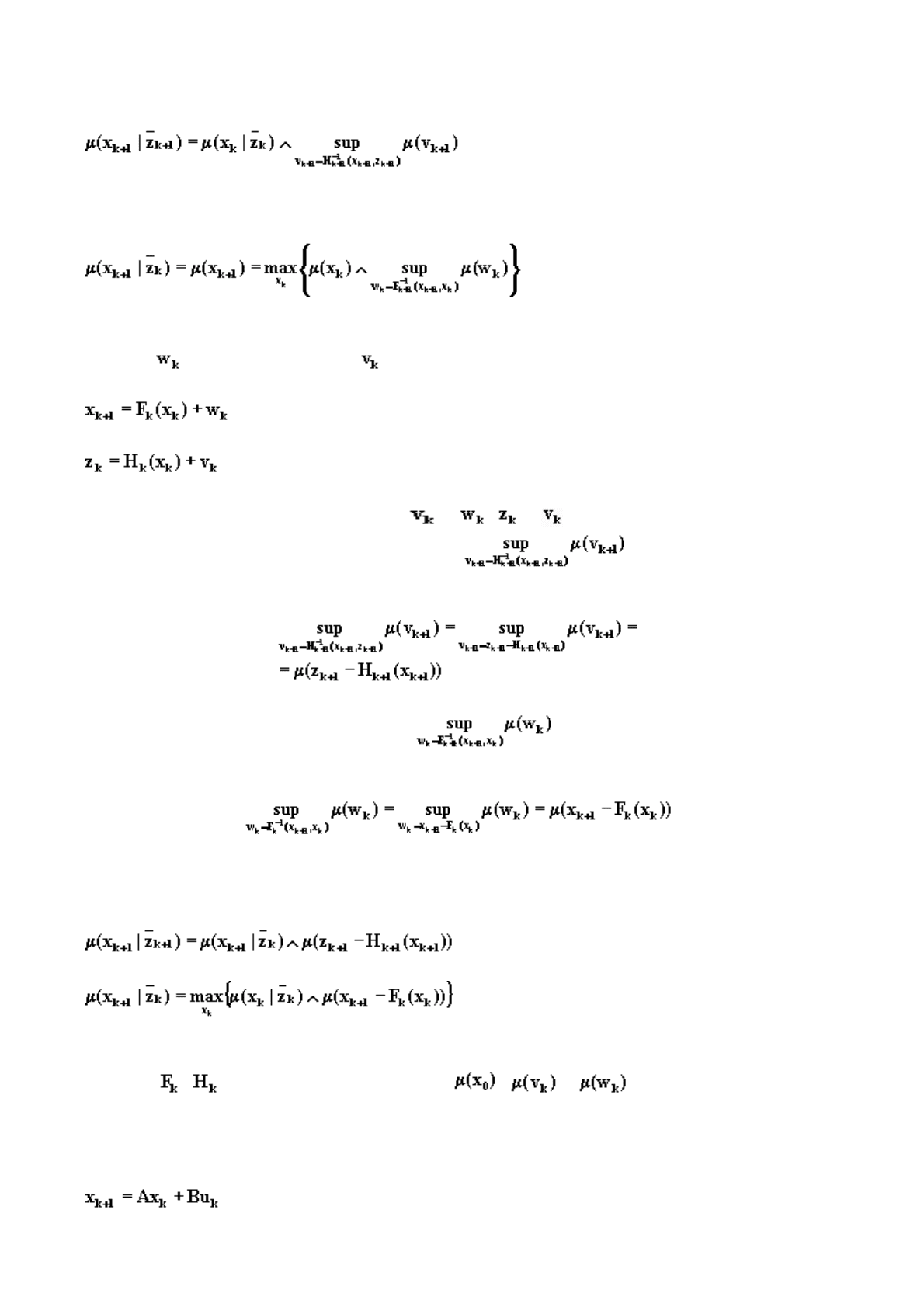
которое для этого случая принимает вид

. (6.92)

Если измерение отсутствует, то рекуррентная процедура сводится к соотношению

. (6.93)

Рекуррентное соотношение имеет особенно простой вид в том случае, когда нечеткие шумы

системы и ошибки измерения входят в (6.84), (6.85) линейно:

; (6.94)

. (6.95)

В этих уравнениях соответствия между и , и являются взаимно однозначными,

поэтому для процедуры (6.90) выражение вида может быть представлено

в следующей форме:

а для уравнения (6.91) выражение вида можно преобразовать следующим

образом:

Тогда рекуррентная процедура (6.90), (6.91) значительно упрощается и может быть

представлена в виде:

; (6.96)

. (6.97)

Рекуррентные соотношения несложно реализуются практически, независимо от видов

функций , и функций принадлежности , и .

В случае управляемой динамической системы также возможно использования имеющейся

модели для задания функции F. Например, в случае линейной модели

(

6.98

)

где на состояние и управление наложены нечеткие ограничения и задана нечеткая цель

функционирования системы, для функций принадлежности с использованием определения

образа нечеткого множества можно записать следующее соотношение:

(6.99)

В процессе функционирования системы в общем случае носитель начального нечеткого

состояния расширяется. Чтобы уменьшить неопределенность ситуации при принятии

ешений необходимо использовать дополнительную информацию о проводимых замерах и

исследованиях в системе.

Предполагается, что прямое измерение всего вектора текущего состояния системы

невозможно, а процесс косвенного наблюдения описывается уравнением

где - нечеткий вектор замеров;

- функция измерений.

Для линейной модели (6.98) и линейного уравнения для замеров

можно записать следующую систему рекуррентных уравнений

; (6.100)

. (6.101)

В общем случае, когда функции F и H нелинейные, уравнения (6.100), (6.101) могут быть

записаны в виде:

; (6.102)

. (6.103)

Рассмотрим теперь принципы управления нечеткой динамической системой для функции F

вида (6.83). Допустим, что на управляющее воздействие в каждый момент времени

наложены нечеткие ограничения , характеризующиеся функцией принадлежности

, и задано начальное состояние . Пусть - нечеткая цель, которую

необходимо достигн

ть в момент в

емени N. Эта цель ха

акте

из

ется

фу

нкцией

принадлежности .

Оптимальные четкие управляющие воздействия могут быть определены

следующим образом [54]:

(6.104)

где

(6.105)

Функция может рассматриваться как функция принадлежности для нечеткой цели

в момент времени N-1, индуцированной конечной целью для момента N. Решение задачи

может быть найдено с использованием метода динамического программирования следующей

екуррентной процедурой для промежуточной цели на момент N-j [54]:

(6.106)

где .

Таким образом, зная текущее нечеткое состояние , нечеткое ограничение и

индуцированную нечеткую цель , на момент времени k можно найти эффективное

четкое

авление по

(

6.104

)

(

6.105

)

ГЛАВА 7. КОНТРОЛЬ И УПРАВЛЕНИЕ

ТЕХНОЛОГИЧЕСКИМИ ПРОЦЕССАМИ

РАЗРАБОТКИ ГАЗОВЫХ

МЕСТОРОЖДЕНИЙ В УСЛОВИЯХ

НЕОПРЕДЕЛЕННОСТИ

7.1. Задачи контроля и управления процессом разработки

газовых месторождений

Рассмотрим примеры использования предложенных методов и алгоритмов теории нечетких

множеств в некоторых конкретных прикладных областях. Одной из ведущих отраслей

топливно-энергетического комплекса страны является газовая промышленность. Главной

базой страны, обеспечивающей более 60% добычи природного газа и весь объем прироста

добычи, является территориально-производственный комплекс расположенный н

территории Тюменской области.

Подавляющее число газовых и газоконденсатных месторождений приурочено к водоносным

пластам и разрабатывается в условиях водонапорного режима. При водонапорном режиме

происходит продвижение в газовую залежь контурной или подошвенной воды. Это приводит

к тому, что через некоторое время скважина или целый куст скважин частично или полностью

блокируются.

Ситуация по контролю и управлению обводнения осложняется значительной погрешностью

замеров технологических параметров, наличием различных видов неопределенности при

ешении задач. Описание таких неопределенностей с применением математического аппарата

нечетких множеств и рассмотрение системы по контролю и управлению обводнения в виде

иерархической модели позволяет координировать решения, принимаемые на каждом уровне

иерархической модели системы и получать четкие решения на каждом из уровней. Создание

высокоэффективной автоматизированной системы по прогнозированию и контролю уровня

газоводяного контакта (

ГВК) позволит продлить срок службы скважин, снять необходимость

доразбуривания месторождения.

В соответствии с проведенной авторами декомпозицией системы газодобычи [134, 135]

можно выделить следующие основные задачи подсистемы управления разработкой газовых

месторождений:

1. задачи обработки различных исследований скважин, расчета технологических и

геолого-промысловых параметров при наличии неточных замеров и моделей [37, 39,

101, 105, 134];

2. задачи прогнозирования падения пластового давления в залежи и продвижения

газоводянного контакта [39, 100, 101, 102, 124, 128, 134, 139, 184, 196];

3. задачи выбора режимов работы газовых скважин, обеспечивающих рациональную

разработку газовых месторождений [26, 39, 101, 134];

4. выдача на графопостроитель карт различных разрезов, изоповерхностей и графиков [17,

134, 189];

5. задача подсчета запасов для газовых месторождений [96, 101, 134];

6. информационное обеспечение пользователей и решаемых задач геолого-промысловыми

и оперативными данными (банк данных геолого-промысловой и оперативной

информации) [17, 85, 134].

В условиях все более широкого внедрения автоматизированных систем управления

азработкой месторождений (АСУ РМ) и перехода к периодическому обслуживанию

установок комплексной подготовки газа (УКПГ) и промыслов Уренгойского и Ямбургского

месторождений, актуальным является вопрос формализации процедуры выбора оптимальных

ежимов работы газовых скважин с учетом неопределенности имеющейся геолого-

промысловой и оперативной информации. К тому же очень часто имеющаяся информация

носит качественный характер и ее сложно учесть в процессе выбора решения по режимам

аботы скважин. Получение решения в виде четкого значения параметров скважин вызывает

сложности при попытке реализации этого точечного решения на практике, т.к. диапазоны

возможного регулирования по дебитам газовых скважин достаточно узкие и в решении не

учтены ограничения со стороны наземного оборудования, межпромыслового коллектора,

ДКС и самой скважины.

Для принятия решений при управлении разработкой группы газовых месторождений

необходима информация о сжатых множествах для дебита скважин и устьевых давлений для

каждого момента времени t , где N - число эксплуатируемых скважин. Это

сжатое множество должно отражать степень эффективности и допустимости дебитов скважин

и соответствующих устьевых давлений с позиций рациональной разработки каждого

отдельного месторождения. В частном случае, когда цели, ограничения и состояние системы

являются нечеткими, сжатое множество становится нечетким и может быть задано функцией

принадлежности .

В свою очередь соответствующее сжатое или нечеткое множество режимов работы отдельной

-ой подсистемы "пласт-скважина" представляет из себя совокупность частных ограничений и

координирующих функций со стороны различных физических процессов. Ввиду нечеткости

всех основных технологических ограничений для подсистемы "пласт - скважина" будем

ассматривать в качестве характеристики функцию принадлежности . Эта функция

может быть записана следующим образом

(7.1)

где - ограничение на режим работы подсистемы "пласт-скважина" j со стороны

возможного разрушения призабойной зоны;

- ограничение на режим работы подсистемы "пласт-скважина" j, которые

накладываются процессом гидратообразования;

- функция принадлежности, характеризующая возможность обводнения

скважины конусом пластовой воды на основе

расчета предельно допустимого дебита

скважины;

фу

нкция п

инадлежности, от

ажающая возможность с

абатывания клапана-

отсекателя при больших дебитах скважины. Эта функция отражает риск срабатывания

клапана-отсекателя, предназначенного для предотвращения свободного фонтанирования

скважины, и может быть построена на основе принципов теории возможностей с

использованием данных о фактических дебитах, на которых происходило срабатывание

клапанов данной конструкции (рис.4.3);

- координирующая F-функция, характеризующая степень принадлежности

ежима работы подсистемы "пласт-скважина" j к подмножеству эффективных режимов с

позиций рациональной разработки газовых месторождений.

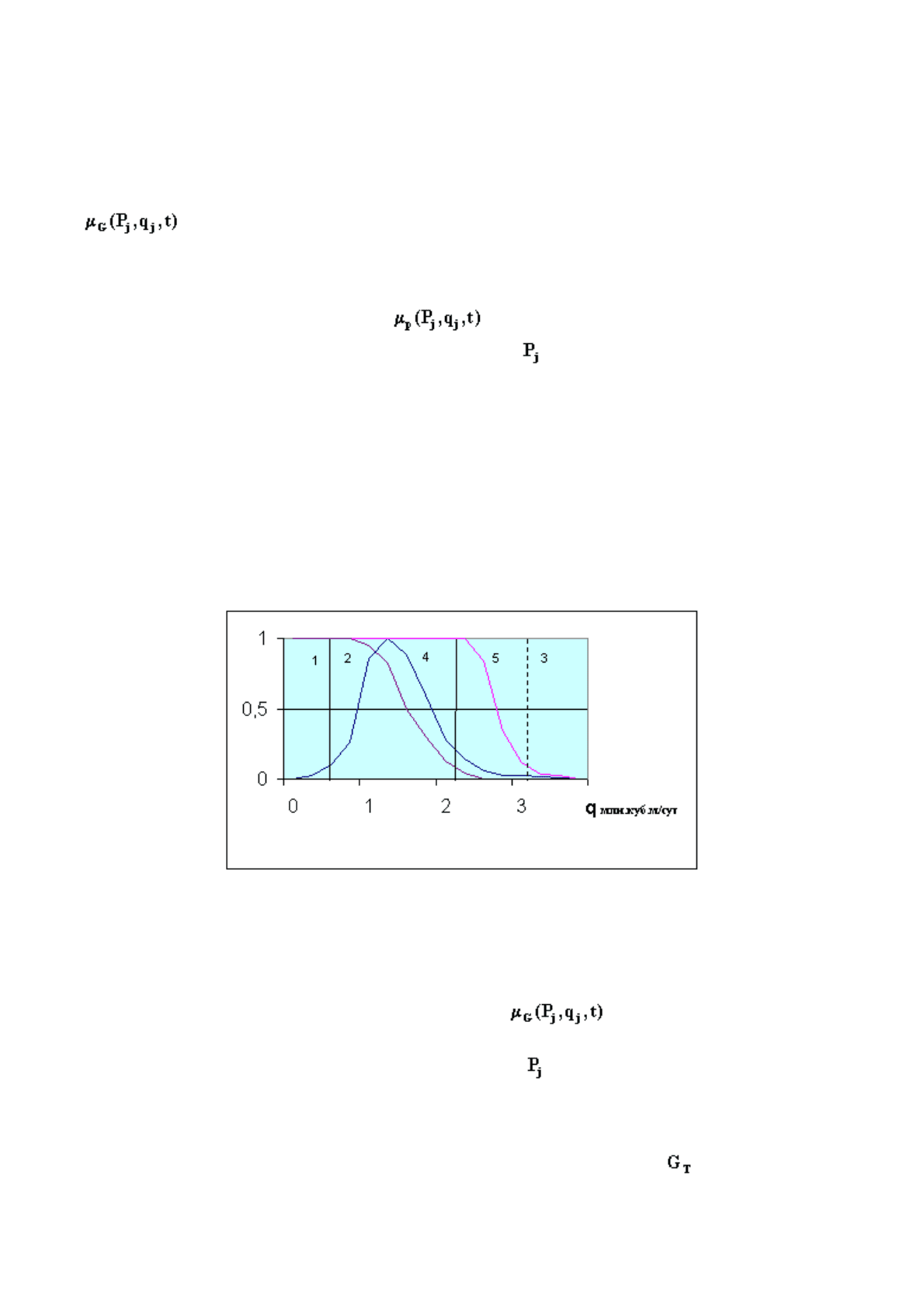
Пример функции принадлежности для одной из скважин месторождений

Тюменского региона при фиксированном значении на момент времени t приведен на

ис.7.1. Приведенные на этом рисунке функции принадлежности характеризуют:

1. четкие ограничения на дебит q газовой скважины со стороны процесса

гидратообразования (1) и разрушения призабойной зоны (3);

2. нечеткие ограничения на дебит q со стороны процесса обводнения конусом пластовой

воды (2) и возможного срабатывания клапана-отсекателя (5);

3. координирующая функция (4) строится с учетом целей рациональной разработки

газового месторождения на

основе принципа нечеткой обратной связи.

Рис.7.1. Функции принадлежности для одной из скважин газового месторождения

Тюменского региона

Первые три функции принадлежности могут быть построены достаточно просто на основе

соответствующих расчетных формул, причем в зависимости от наличия в этих формулах

интервальных или нечетких величин применяются соответствующие операции. Наиболее

сложной является процедура построения F-функции , которая зависит от вектора

состояния каждой подсистемы "пласт-скважина", т.е. от имеющихся запасов газа в зоне

дренирования скважины j, пластового давления и от стадии обводнения зоны

дренирования скважины пластовой водой.

Под целью G может также подразумеваться и более сложное понятие - достижение системой

к моменту окончания разработки месторождения T нечеткой цели . Фактически эта

нечеткая цель является формализованным представлением критерия максимизации конечного

коэ

фф

ициента газоотдачи место

ождения. Под

обное

ешение этой задачи с п

именением