Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях

Подождите немного. Документ загружается.

Выполнение всех этих гипотез обычно проверяется для каждого конкретного случая

применения этой модели. Вполне естественно, что точное выполнение гипотез на практике

отсутствует, а соответствующие количественные характеристики степени применимости

модели для каждой конкретной ситуации отсутствуют и в модель объекта они не включаются.

Между тем такие характеристики очень важны, особенно при наличии нескольких моделей

или многоуровневой системы моделей и необходимости их согласования и координации. В

данном случае в качестве языка, позволяющего провести согласование в условиях

неопределенности и многоуровневости моделей, применяется теория нечетких множеств.

Пусть решение по каждой из

модели задано нечетким множеством

на множестве

ешений

, тогда согласованное решение

может быть представлено как пересечение

частных решений

Для каждого нечеткого решения

будет задаваться функция принадлежности .

После нахождения системного решения могут быть скорректированы (скоординированы)

исходные функции принадлежности.

Коррекция исходных нечетких величин

В общем случае задача коррекции исходных нечетких величин записывается следующим

образом. Пусть имеется системное нечеткое решение

полученное в результате согласования нечетких решений и для моделей 1 и 2.

Исходные нечеткие параметры для модели

1 заданы функциями , для которых

определено, что

где

- арифметическая операция.

Необходимо получить скорректированные функции , для которых выполняется

условие

Алгоритм решения достаточно рассмотреть для случая

n=2

, поскольку для

n>2

процесс

коррекции сводится к последовательному применению данного простейшего алгоритма.

сть

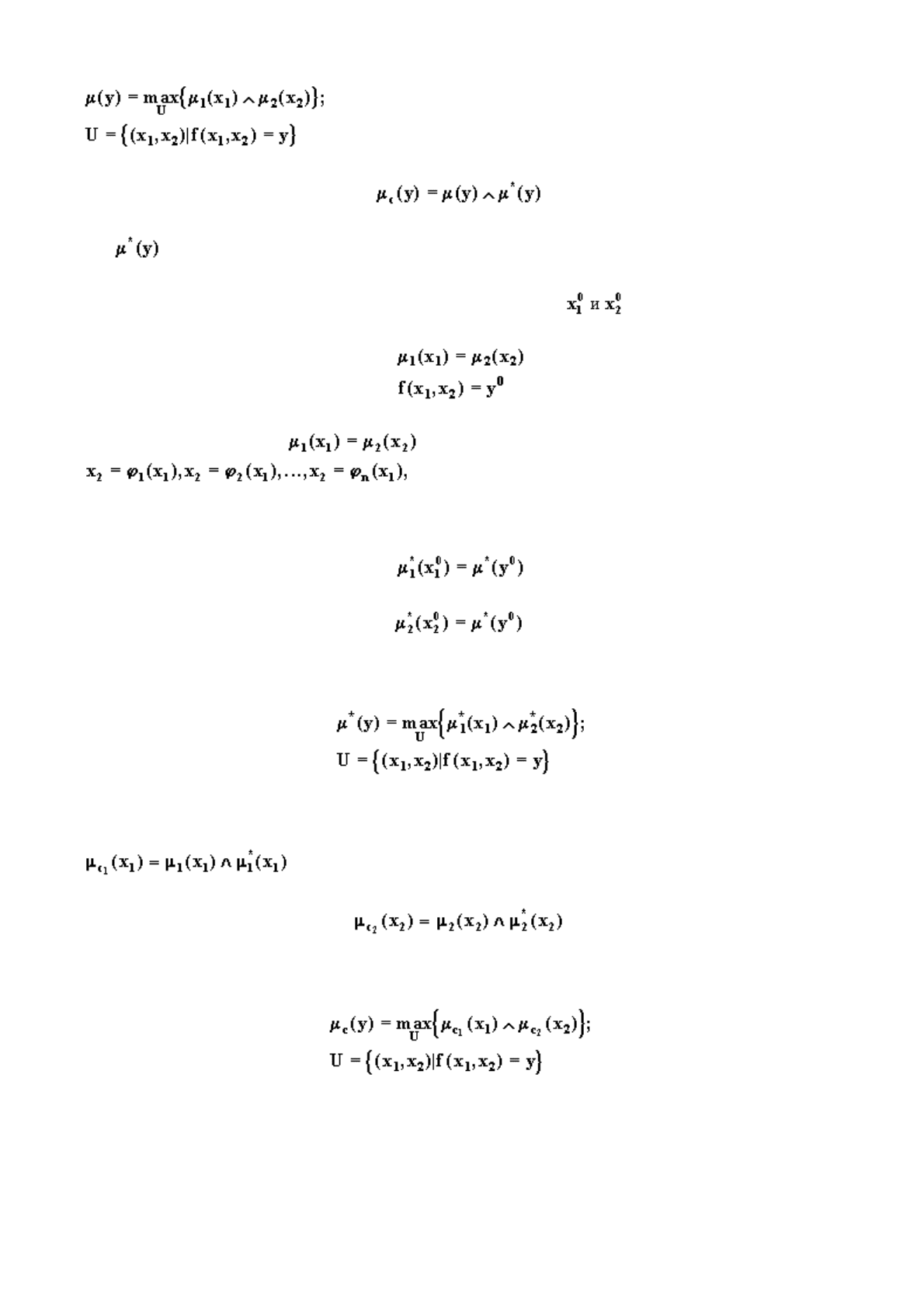
(5.35)

где - корректирующая функция (например, функция предпочтения центра).

1. Для произвольного фиксированного

находим решение из системы уравнений

Если соотношение распадается на несколько зависимостей

то выбирается та, для которой выполняется (5.35).

2. Полагаем

Тогда справедливо равенство

Обозначим

(5.36)

тогда

На основе данного метода нетрудно построить численные процедуры коррекции.

Коррекция по носителю

Для проведения коррекции по носителю для выбранных числовых значений

, y

, ..., y

используется приведенный выше метод коррекции, который в этом случае может быть

сокращен, так как отпадает необходимость выполнения 3-го этапа. Это происходит потому,

что

можно задавать только на , поскольку . Более того, если

, то

задается в той части носителя, где .

Коррекция по r-уровням

Разобьем интервал на

m r

-уровней точками

, i=1, m

. Из решения уравнений

определяются

-уровневые множества .

Находятся

-уровненвые множества для функции и из решения двух систем

уравнений

(5.37)

(5.38)

откуда

где - решения систем уравнений (5.37) и (5.38) соответственно.

Поскольку и известны, то из (5.36) находятся

-уровненвые множества для

и .

Алгоритм также можно упростить, если разбивать

-уровнями интервал

[0,

]

, где

и решать

систем

где

определяется из уравнения .

Если функции и заданы не аналитически, а дискретно по

-уровням, то в

алгоритме коррекции первые два пункта не выполняются, а третий пункт изменяется

следующим образом. Для нахождения

-уровневых множеств функций и

функциональная зависимость

линеаризуется для соответствующего

-уровня. Тогда уравнения (5.37) и (5.38) принимают

следующий вид:

Причем, для выполняются следующие равенства

Уравнения при дискретном задании функций и можно

аппроксимировать и нелинейной зависимостью, однако для практических расчетов линейная

апп

оксимация дает достаточно п

иемлемые

ез

льтаты.

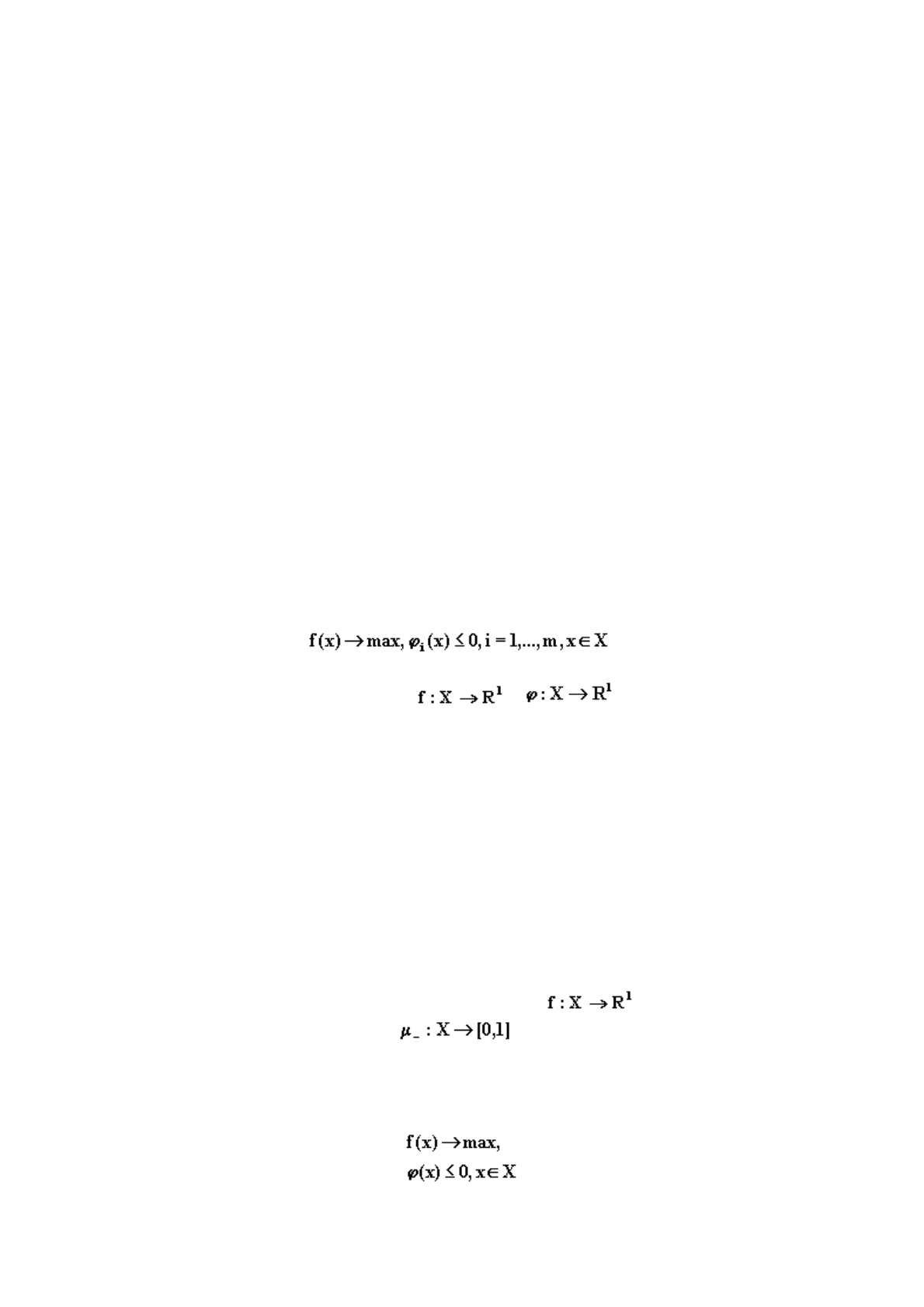
ГЛАВА 6. АЛГОРИТМЫ НЕЧЕТКОГО

ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

6.1. Характеристика задач нечеткого математического

программирования

Классическое математическое программирование и его разновидности - в значительной

степени нормативная методология эффективного выбора. Нечеткое же программирование

выделяет естественную множественность неточно определенных целей, значений и

ограничений. При этом оптимальность определяется и в терминах поведения, и как качество,

присущее решению.

Главная цель нечеткого математического программирования (НМП) - помочь лицу,

принимающему решение, разобраться в выдвинутых им допущениях. Нечеткий подход не

подменяет собой простейшего анализа в поисках разумной точности. Он облегчает задачу

лица, принимающего решения, позволяя ему не формулировать явно точные ограничения.

Вот почему плодотворный обмен идеями между теорией нечетких множеств и классическим

программированием может явиться значительным шагом к созданию новых методов.

Стандартная задача нечеткого математического программирования формулируется обычно

как задача максимизации (или минимизации) заданной функции на заданном множестве

допустимых альтернатив, которое описывается системой равенств или неравенств. Например:

где

- заданное множество альтернатив, и - заданные функции.

При моделировании в нечеткой форме реальных задач принятия решений в распоряжении

исследователя - математика могут оказаться лишь нечеткие описания функции f и

параметров

, от которых зависят эти функции, да и самого множества Х. Таким образом,

задача стандартного математического программирования превратится в задачу нечеткого

математического программирования.

Формы нечеткого описания исходной информации в задачах принятия решений могут быть

азличными; отсюда и различия в математических формулировках соответствующих задач

нечеткого математического программирования.

Перечислим некоторые из таких постановок [179].

Задача 1.

Максимизация заданной обычной функции на заданном нечетком

ножестве допустимых альтернатив .

Задача 2.

Нечеткий вариант стандартной задачи математического программирования.

усть определена следующая задача математического программирования:

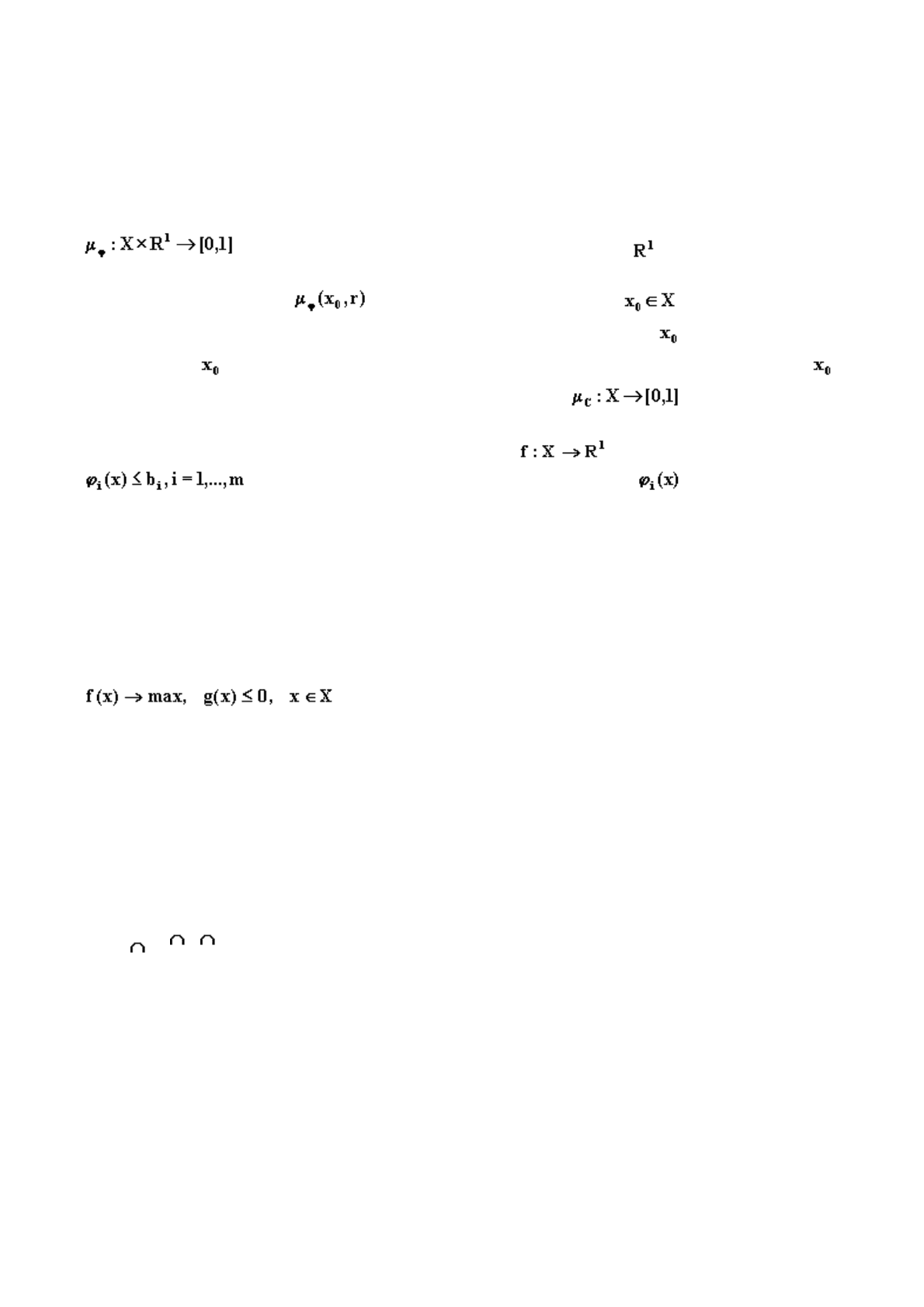
Нечеткий вариант этой задачи получается, если “смягчить” ограничения, т.е. допустить

возможность их нарушения с той или иной степенью. Кроме того, вместо максимизации

функции f(х) можно стремиться к достижению некоторого заданного значения этой функции,

причем различным отклонениям значения функции от этой величины приписывать различные

степени допустимости.

Задача 3.

Нечетко описана “максимизируемая” функция, т.е. задано отображение

,где

- универсальное множество альтернатив, - числовая ось.

В этом случае функция при каждом фиксированном представляет собой

нечеткое описание оценки результата выбора альтернативы (нечеткую оценку

альтернативы ) или нечетко известную реакцию управляемой системы на управление .

Задано так же нечеткое множество допустимых альтернатив .

Задача 4.

Заданы обычная максимизируемая функция и система ограничений вида

, причем параметры в описаниях функций заданы в форме

нечетких множеств.

Задача 5.

Нечетко описаны как параметры функций,определяющих ограничения задачи, так

и самой максимизируемой функции.

Рассмотрим, например подробнее задачу линейного программирования с нечёткими

коэффициентами. Нечеткость в постановке задачи математического программирования может

содержаться как в описании множества альтернатив, так и в описании целевой функции.

(6.1)

На практике часто сталкиваются с применением точной теории оптимизации к неточным

моделям, где нет оснований писать точно определенные числа и где слишком часто

появляются трудности вычислительного характера при описании больших систем.

Нечеткую обстановку можно рассматривать как множество

альтернатив вместе с его

нечеткими подмножествами

, представляющими собой нечетко сформулированные критерии

(цели и ограничения), т.е. как систему

(Х, f

, f

, ..., f

)

. Принять во внимание по возможности

все критерии в такой задаче означает построить функцию

D = f

... f

, (6.2)

в которую цели и ограничения входят одинаковым образом.

Решение можно определить как нечеткое подмножество универсального множества

альтернатив. Оптимум соответствует той области

, элементы которой максимизируют

Это и есть случай нечеткого математического программирования.

Очевидно, неразумно в реальных ситуациях проводить резкую границу для множества

допустимых альтернатив, поскольку может случится так, что распределения, лежащие за этой

границей, дадут эффект, превышающий меньшую желательность для лица принимающего

ешения.

Например, ясно, что при несовместных распределениях эта область пустая. В этом случае

налицо необходимость модификации ограничений. Желательно выяснить, как изменить

ограничения задачи, чтобы появились допустимые решения и задача стала разрешимой.

В таких случаях представляется целесообразным вводить нечеткое множество допустимых

элементов и, следовательно, рассматривать проблему как задачу НМП с применением

подхода, дающего человеку больше свободы в использовании его субъективных

представлений о ситуации.

Формы нечеткого описания исходной информации в задачах принятия решений могут быть

азличными; отсюда и различия в математических формулировках соответствующих задач

НМП.

Нечеткий вариант стандартной задачи математического программирования получается, если

"смягчить" ограничения, т.е. допустить возможность их нарушения с той или иной степенью.

Кроме того, вместо максимизации целевой функции

f(x)

можно стремиться к достижению

некоторого заданного ее значения, причем различным отклонениям значения

f(x)

от этой

величины приписывать различные степени допустимости (например, чем больше отклонение,

тем меньше степень его допустимости).

Пусть

- заданная величина функции цели

f(x)

, достижение которой считается достаточным

для выполнения цели принятия решений, и пусть имеется пороговый уровень

такой, что

неравенство

f(x) < a-b

означает сильное нарушение неравенства

f(x) a

. Тогда функцию

принадлежности

для нечеткой функции цели можно определить следующим образом:

(6.3)

где

- функция принадлежности, описывающая степени выполнения соответствующего

неравенства с точки зрения лица, принимающего решения.

Аналогично определяется функция принадлежности для нечетких ограничений. В

езультате исходная задача оказывается сформулированной в форме задачи выполнения

нечетко определенной цели, к которой применим подход Беллмана - Заде (6.2).

При моделировании ситуации в форме задачи линейного программирования

(6.4)

о коэффициентах

, b

известно лишь то, что они находятся в некотором множестве,

отражающем все реальные возможности.

В некоторых случаях точное описанное множество ограничений (допустимых альтернатив)

может оказаться лишь приближением реальности в том смысле, что в реальной задаче

альтернативы вне множества ограничений могут не допустимыми, а лишь в той или иной

степени менее желательными

для лица, принимающего решения, чем альтернативы внутри

этого множества.

Рассмот

им задач

нахождения миним

ма на заданной области. П

сть задана область вид

, (6.5)

где - нечеткие подмножества множества

, а бинарная операция

обозначает

сложение нечетких множеств.

Требуется найти на заданной области.

Коэффициент при каждой переменной в ограничениях можно считать функцией полезности,

определенной на числовой оси. Можно считать, что эти коэффициенты дают субъективную

оценку различных возможностей, включая таким образом другие, не определенные

ограничения.

Сведём решение исходной задачи к решению ряда задач линейного программирования. Для

этого введём дискретные

-уровни. В результате нечёткие ограничения принимают

следующий интервальный вид:

(6.6)

Т.о., мы перешли от нечётких множеств к чётко определённым и теперь, зная, что

обычный

интервал, можем записать нашу задачу в следующем виде (случай 2

2 ):

(а

, а

) x

+ (c

, с

) x

, b

)

(а

, а

) x

+ (с

, с

) x

, b

)

(6.7)

Теперь, чтобы привести задачу к виду обычной задаче линейного программирования, нам

достаточно записать неравенства отдельно по левому и правому краям интервалов, с учётом

знаков неравенства. Т.е., мы приведём систему к следующему виду:

+ с

+ c

(6.8)

+ c

С помощью несложных преобразований мы перешли от задачи с нечёткими коэффициентами

к задаче линейного программирования с чёткими коэффициентами, при этом количество

ограничений увеличилось в два раза и полученную задачу мы можем решить симплексным

методом.

Таким образом, из рассмотренного примера явно просматривается алгоритм решения задачи с

нечеткими коэффициентами. Следуя ходу рассуждений в

данном примере, составим алгоритм

ешения задачи. Он имеет вид:

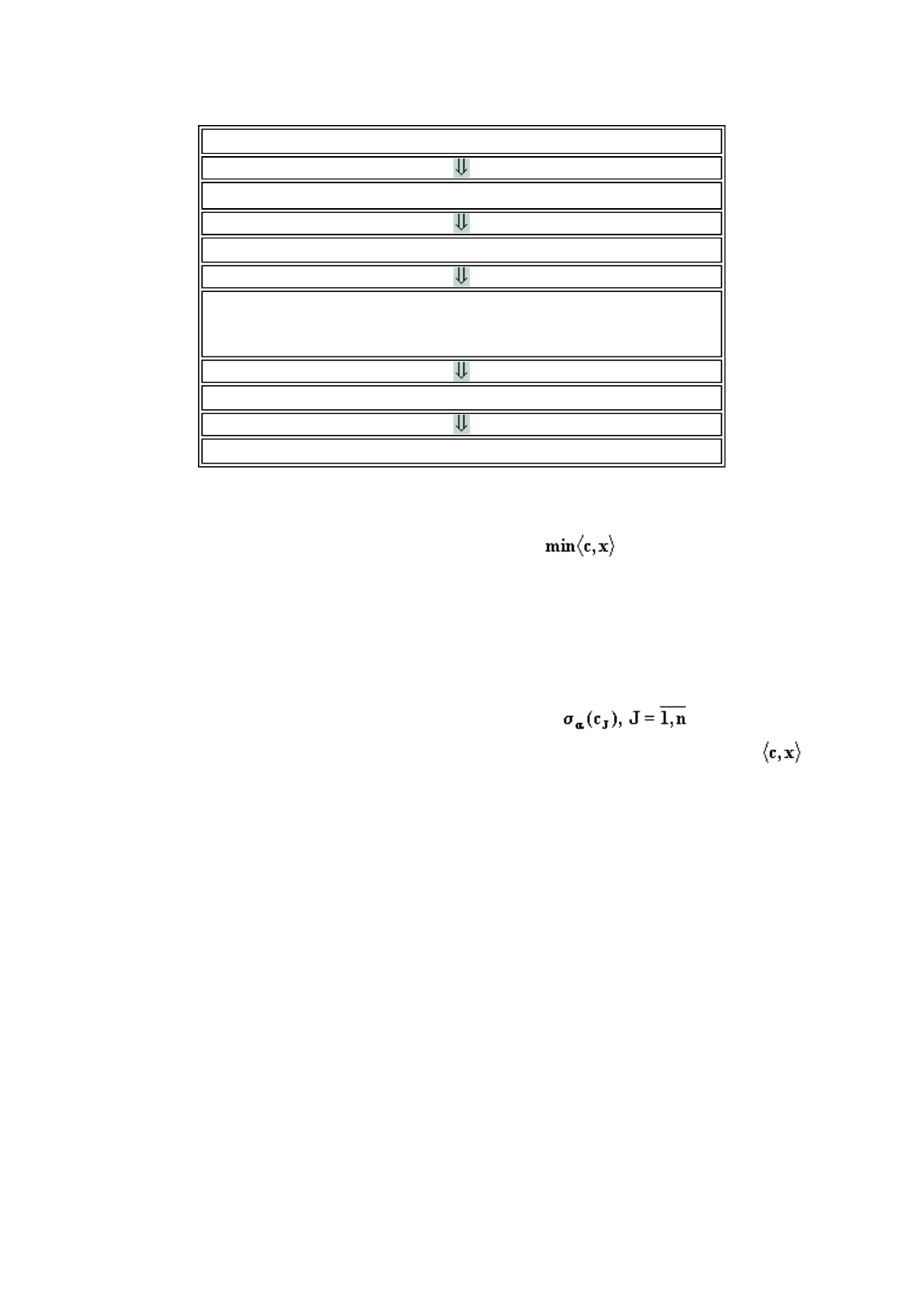
Как видим, исходная задача НМП представляется в виде совокупности обычных задач

линейного программирования на всевозможных множествах уровня множества допустимых

альтернатив. Если альтернатива

есть решение задачи на множестве уровня

, то

можно считать что число

есть степень принадлежности альтернативы

нечеткому

множеству решений исходной задачи. Перебрав таким образом всевозможные значения

получаем функцию принадлежности нечеткого решения.

Если же и компоненты целевой функции

являются нечеткими, то необходимо выбирать для

каждого уровня

соответствующие границы множеств в соответствии с

правилами интервальной арифметики, минимизируя предварительно таким образом .

Из данного примера видно, что за гибкость приходится платить ценой увеличения

азмерности задачи. Фактически исходная задача с ограничениями по включению

преобразуется в задачу с ограничениями в виде неравенств, с которыми легко обращаться;

при этом такая цена не слишком высока, поскольку сохраняется возможность использования

хорошо разработанных классических методов.

6.2. Численные методы решения задач нелинейного,

линейного, нечеткого и интервального программирования

В реальной жизни мы чаще сталкиваемся со сложными системами, имеющими

иерархическую структуру. Размерность таких задач, как правило, бывает очень велика, что

создает трудности для применения к подобным системам симплекс-метода. Решение таких

систем симплекс-методом без их преобразования - это очень трудоемкая процедура, которая к

тому же даже на современных вычислительных машинах занимает много времени. Это делает

практически невозможным решение таких задач без специальных методов.

Поэтому к таким системам обычно применяют методы декомпозиции, т.е. “большую” задачу

азбивают на необходимое число меньших подзадач и решают симплекс-методом уже ее

подзадачи, а затем сводят к

ешению пе

воначальной задачи.

исходная задача

вводим дискретные

- уровни

ограничения принимают интервальный вид

записываем неравенства отдельно по левому и правому краям с

учетом знаков неравенства

(при этом размерность увеличивается)

получаем задачу ЛП с четкими коэффициентами

решаем полученную задачу симплекс - методом

В таком подходе тоже есть свои сложности, потому что не всякая система может быть разбита

на подзадачи. Это налагает определенные ограничения и требования на исходную задачу и

возможность решения задачи зависит от структуры матрицы задачи.

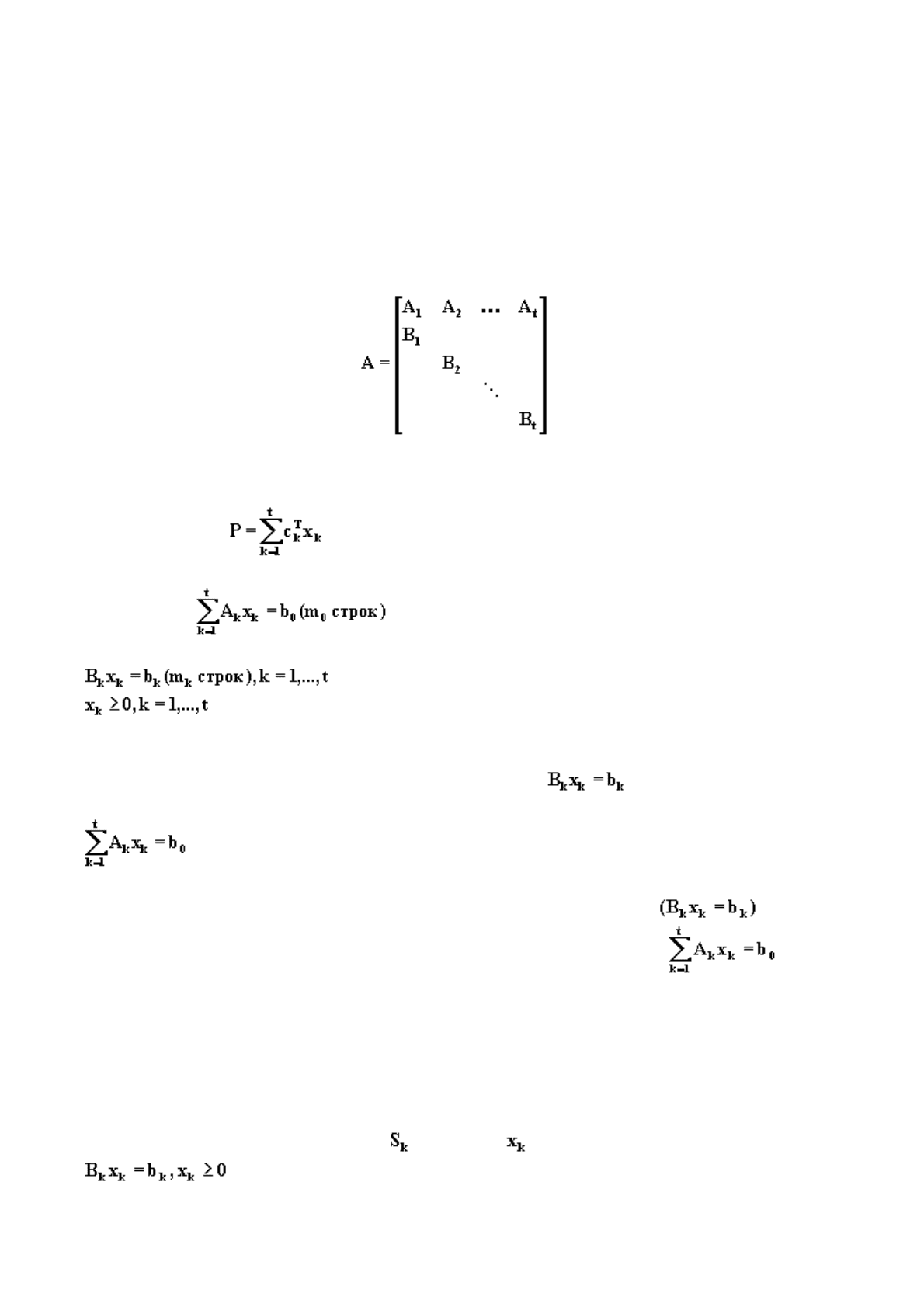
Существуют различные виды декомпозиционных методов в соответствии со структурой

матрицы ограничений

. Наиболее часто встречающаяся структура, поддающаяся

азложению, - это так называемая блочно-диагональная система, которая представляет собой

серию блочно-диагональных подматриц, связанных группой ограничений общего вида,

именно:

Задача с такой структурой матрицы ограничений может быть записана следующим образом:

максимизировать (6.9)

при условиях (6.10)

(6.11)

Такая структура возникает естественным образом в моделях, которые описывают процесс,

азбитый на несколько стадий, когда ограничения заключают в себе все

ограничения, относящиеся к периоду k=1,...,t, а группа связывающих ограничений

относится к условиям, имеющим силу в течение всего планового периода.

Описанная выше структура возникает также при моделировании иерархических систем, где

каждая полуавтономная система имеет свои собственные ограничения и в то же

время подчиняется доминирующим организационным ограничениям . Ясно,

что, если каким-то образом избавиться от связывающих ограничений, задачу можно решить,

ешив t меньших подзадач.

етод Данцига-Вулфа

, разработанный для достижения этой цели, основан на понятии

генерации столбцов, которое означает, что небазисные столбцы матрицы А, необходимые для

вычисления относительных оценок, генерируются только по мере необходимости.

Предположим, что множество точек , удовлетворяющих ограничениям

, является замкнутым и ограниченным (мы можем всегда обеспечить

замкн

тость и ог

аниченность множеств

, наложив соответств

ющее ог

аничение све

на