Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях

Подождите немного. Документ загружается.

[229]. При наличии векторного критерия применение этих методов оптимизации возможно

только путем синтеза (чаще всего аддитивного) одного обобщенного критерия из частных

критериев или введением всех (кроме основного) критериев в качестве дополнительных

ограничений или штрафных функций.

Необходимость перевода векторного критерия в скалярный критерий оптимизации привела к

введению специальных функций предпочтения решений, т.е. акцент все больше переносится

на проблему предварительного определения преимущества того или иного решения [162].

Наиболее часто при решении многокритериальных задач применяются синтетические

показатели качества - аддитивные, мультипликативные и минимаксные критерии.

Аддитивный глобальный критерий качества определяется следующим образом :

, (5.2)

где N - число частных критериев эффективности, причем в частном случае могут

использоваться и дополнительные условия нормировки

и . (5.3)

Весовые коэффициенты для частных критериев подбираются субъективно, на основе

экспертных оценок, однако имеются и методы объективного определения весов (например, из

ешения статистической игры с критерием минимизации экономических потерь при принятии

ешений [80]).

Основным недостатком аддитивного критерия является возможность компенсации одного

критерия за счет других.

Мультипликативный глобальный критерий имеет вид

(5.4)

а минимаксный

. (5.5)

Мультипликативный критерий не допускает компенсации, и если значение одного из частных

критериев равно нулю, то глобальный критерий также равен нулю. К достоинствам

минимаксного критерия можно отнести тот факт, что для него не происходит смещения

оптимума при добавлении новых несущественных критериев, но в тоже время он ухудшает

чувствительность глобального критерия.

При возможности ранжирования критериев по важности для нахождения численного решения

нередко применяется метод последовательных уступок.

Если в системе имеется неоп

еделенность, то задача п

инятия

ешения значительно

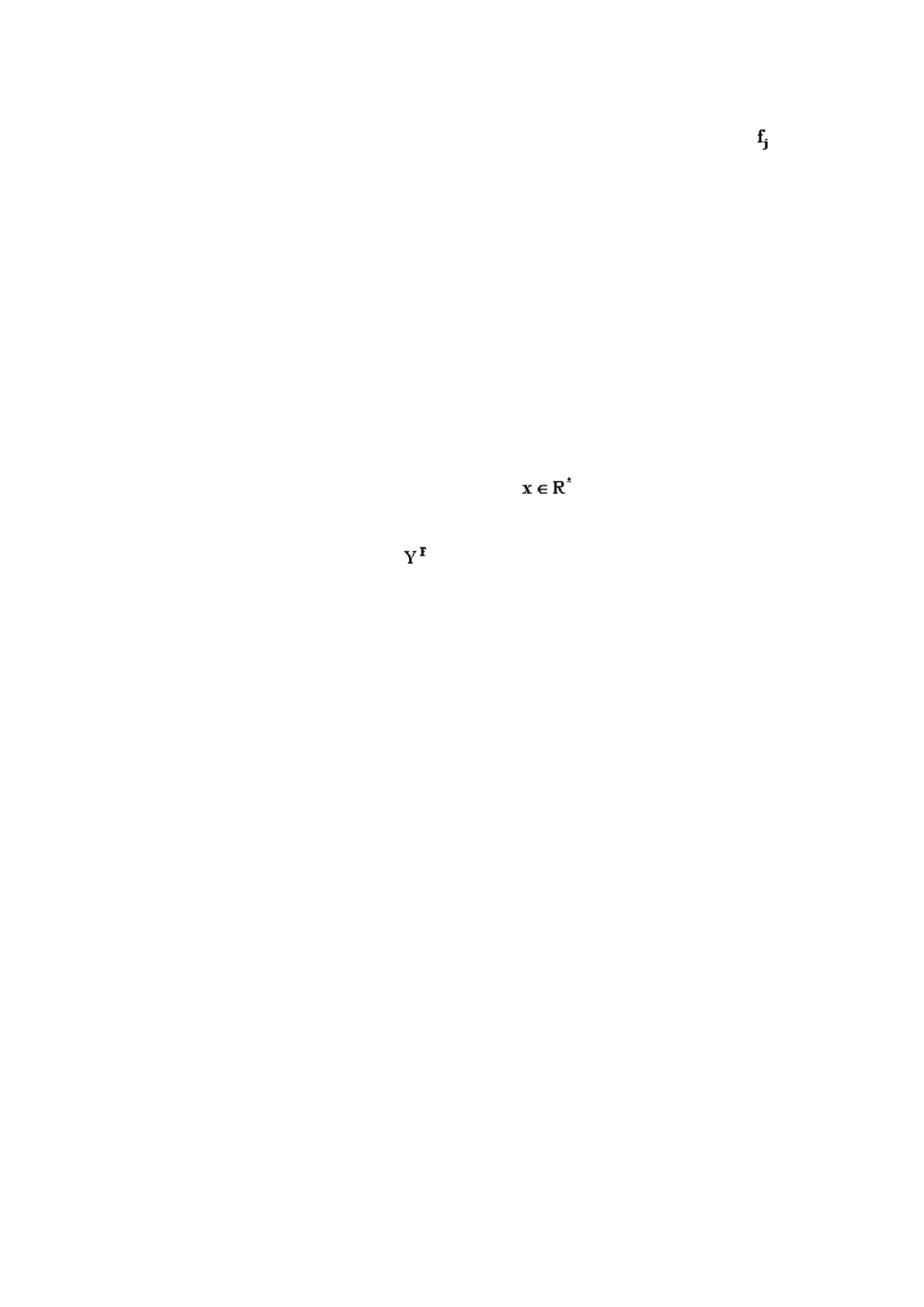
усложняется. В случае статистической неопределенности (при известных распределениях

случайных параметров) при наличии векторной целевой функции решение обычно

характеризуется не одним, а несколькими числами и роль целевых функций играют

определенные параметры распределения, причем наиболее известными примерами являются

математическое ожидание М и дисперсия D, моменты высших порядков применяются редко.

Иногда применяются и обычные функционалы, определенные на множестве решений, однако

эти критерии уже носят вероятностный характер: они означают вероятности появления

некоторых событий (например, вероятность безотказной работы оборудования и т.д.).

В работе [9] проводится анализ и обобщение существующих алгоритмов координации на

основании следующих введенных понятий:

1. множество эффективных точек Р* или множества Парето (обладающих тем свойством,

что невозможно улучшить значение какого-либо частного критерия для подсистемы по

сравнению со значением, достигаемым этим критерием в точке х, без ухудшения

значения хотя бы одного из прочих частных критериев);

2. множество полуэффективных точек

(если , то не существует допустимой

альтернативы, улучшающей значение сразу всех частных критериев);

3. множество допустимых значений критериев.

Одним из существенных достоинств решения многокритериальной задачи является тот факт,

что в результате решения однокритериальной задачи мы получаем решение на границе

какого-либо ограничения, т.е. она по сути представляет собой "генератор" узких мест,

которые "болезненно" отражаются на поведении реального объекта и значительно снижают

другие показатели режима работы системы - надежность, оптимальность и т.д.

Многокритериальная постановка задачи отличается большей близостью к реальной задаче и

меньшей долей абстракции [130].

Для реальных систем характерна зависимость выбора критерия (или группы критериев)

оптимизация от окружающей среды и ряда других факторов; т.е. в зависимости от ситуации

должен проводиться выбор вектора критериев (или одного критерия) в процессе принятия

ешения оптимальным образом, а не вводиться в систему жестко или волевым путем. Особо

важное значение приобретают вопросы анализа зоны применимости различных критериев и

выявления возможности решения однокритериальных задач в частном случае. Поэтому

становится возможным объективно провести выбор критериев по степени их применимости.

Одним из существенных достоинств метода оптимизации можно считать тот факт, что

изменение критерия оптимизаций и переход к векторной оптимизации, изменение

ограничений не приводит к переходу к совершенно новой задаче и даже к смене метода

ешения задачи, т.е. метод оптимизации должен обладать достаточной гибкостью.

В настоящее время принят такой подход к постановкам задачи, что критерии принятия

ешений не входят в модель и задаются человеком до начала решения задачи на ЭВМ.

Однако субъективизм выбора критерия крайне велик в этом случае. Выбор того или иного

критерия полностью определяется состоянием системы и внешней среды, а также степенью

неопределенности по различным показателям, параметрам и характеристикам системы.

Рассматривая концептуальные уровни описания сложной

иерархической плохо определенной

системы согласно [259] можно выделить три уровня описания с характерной для каждого из

них степенью абстрагирования и детализации:

Методологический

ур

овень

. Использование на этом

ур

овне тео

ии сжатых множеств

позволяет адекватно отобразить задачу управления сложным многоуровневым иерархическим

комплексом, провести декомпозицию этой задачи на ряд более простых иерархических

взаимодействующих задач с использованием основных операций сжатых множеств [49].

Алгоритмический уровень

. С учетом имеющейся в системе неопределенности могут быть

использованы детерминированные методы, теории нечетких, интервальных или случайных

множеств. В данной работе основное внимание уделяется алгоритмам принятия решения на

базе теории нечетких множеств [98] и интервального анализа [247]. Применение теории

нечетких множеств позволяет построить конструктивные алгоритмы для расчета,

идентификации и оптимизации для каждой из полученных с помощью сжатых множеств

задач.

Операциональный уровень

. Для расчета и оптимизации на основе полученных на втором

уровне алгоритмов необходимо иметь аналитические и численные методы оперирования с

нечетким и интервальными величинами, методы решения задач нечеткого и интервального

линейного и нелинейного программирования, получения решений систем обычных и

дифференциальных уравнений. Имеются также различные способы сведения задач нечеткого

математического программирования к совокупности задач интервального программирования,

а также к обычным детерминированным задачам, что дает возможность воспользоваться

хорошо разработанными методами и пакетами программ математического программирования

[166]. Требуются также конструктивные методы построения функций принадлежности.

5.3. Применение теории сжатых множеств для

декомпозиции процесса управления

Вначале, следуя [344], выделим набор основных операций, последовательным применением

которых может быть осуществлена декомпозиция процесса управления сложной

многоуровневой системы на ряд иерархически взаимосвязанных задач. В отличие от

существующих методов синтеза задач вышестоящего уровня на основе первоначально

определенных задач нижнего уровня управления используемый метод декомпозиции

начинает с концентрирования на глобальной задаче управления всей системой в целом.

Преимущество этого метода заключается в том, что обоснованно вводятся (и если это

необходимо, контролируются) различные упрощения в процессе декомпозиции общей задачи

на подзадачи каждого уровня. Важно понять все эти упрощения, так как они могут подсказать

способ координации подсистем и учета влияния неопределенностей различного типа. При

проведении декомпозиции будем оперировать

с задачами, определение которых шире

понятия "модель системы", так как включает в себя цели управления системой, возмущения

внешней среды и описание всех видов неопределенностей, возникающих на разных стадиях

автоматизации системы. Задача отражает дополнительные цели, ограничения и структурные

изменения в системе, связанные с взаимодействием подсистем в процессе реализации целей

управления в условиях

неопределенности.

Общая задача управления может быть разделена между подсистемами разных уровней с

использованием слабых взаимодействий между отдельными частями системы или между

азличными составляющими целевой функции. Иерархическая структура системы

управления появляется в результате декомпозиции общей задачи управления.

Взаимодействие между регуляторами отображается во взаимосвязь подзадач. Структура

иерархического управления системой будет соответствовать структуре решения отдельных

подзадач. Слабые взаимодействия могут быть определены и на основе анализа

неопределенности информации в системе, наличия фактически замеряемых параметров.

ез

льтате декомпозиции общая задача

авления

азбивается на ие

хические

подзадачи таким образом, что некоторые подзадачи могут быть решены не требуя

информации от других подзадач, зависящих от их решения. Сохраняется лишь

информативный поток, помогающий вышестоящим регуляторам выбирать соответствующую

подзадачу в зависимости от ситуации на объектах путем анализа допустимости принятых

аппроксимаций и упрощений и посредством этого улучшать работу иерархической системе

управления. В зависимости от сложности алгоритма анализа и регулятора нижестоящего

уровня поток информации может меняться от информации о классифицировании ситуации до

полной информации, замеряемой этим уровнем.

Сама декомпозиция заключается в замене задачи на эквивалентную совокупность подзадач.

Декомпозиция проводится через ряд последовательных стадий, в которых формулируются

промежуточные задачи. Некоторые стадии могут быть связаны с преобразованием задач в

форму, подходящую для декомпозиции; разделением задач, а также дальнейшим

объединением в единые задачи образовавшихся в результате декомпозиции эквивалентных

подзадач.

Критерием эквивалентности двух задач является наличие одинаковых решений. Поэтому

полезно характеризовать каждую задачу в терминах ее решения. Причем это возможно без

получения конкретного решения косвенным образом, так что решение задачи

, (5.6)

будет теперь характеризоваться неявным множеством

(5.7)

Решение определяется как множество, т.к. оно не всегда единственное. Это выражение

определяет элементы множества без формирования точных значений этих элементов.

Представленная на таком формальном уровне задача может рассматриваться как особый тип

множеств, известных как сжатые множества [344]. Прилагательное "сжатое" используется

ввиду того, что множество может быть представлено как "сжатие" ограниченного множества

Х, которое отображает целевую функцию (функционал) V в максимальный элемент в области

определения V. Это множество отличается от других множеств в том, что оно определяется

косвенным образом и его условия определения включают оптимизацию.

Сжатое множество

будем обозначать и определять формально как

(5.8)

где V - однозначная скалярная функция или функционал, отображающий Х на линейно-

упорядоченное множество П:

. (5.9)

Очевидно, что . Более того, если только один элемент из Х отображается V в

максимальный элемент множества П, то содержит один элемент х*, что

соответствует задаче имеющей единственное решение. Аналогично, если П имеет

минимальный элемент, то можно определить подмножество Х, которое отображает V в этот

минимальный элемент:

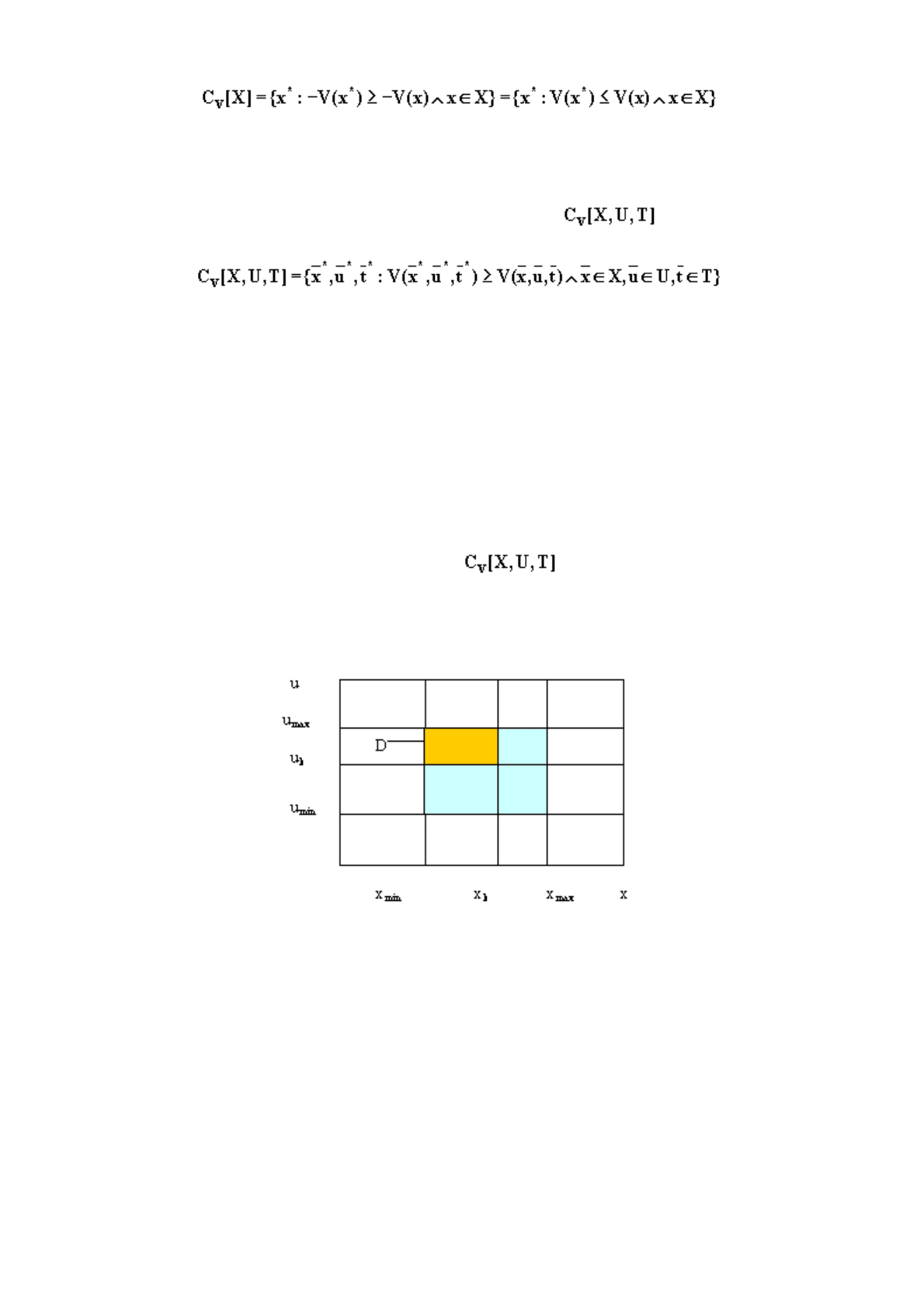
Следовательно, как задачи минимизации, так и задачи максимизации характеризуются своими

сжатыми множествами.

Применим в качестве базового понятие сжатого множества :

где V - функционал, отображающий множества Х,U,Т на линейно-упорядоченное множество

П.

Существует несколько видов сжатия множества допустимых режимов Х и управляющих

воздействий U.

Сжатие может быть в системе естественным при наличии в ней локальных устройств

автоматики, АСУ ТП, операторов и диспетчеров, наделенных правом принимать решения и

осуществлять регулирование технологического процесса в рамках определенных для них

верхним уровнем уставок и ограничений.

Возможны несколько видов сжатия множества :

1. Отсечение на множествах управлений U и состояний Х в процессе согласования режимов

(рис.5.1).

Рис.5.1. Сжатие множества в процессе согласования

режимов.

2. Наличие моделей и взаимосвязей между параметрами состояния и управлением также

позволяет сжать множество

ежимов

(

ис.5.2

)

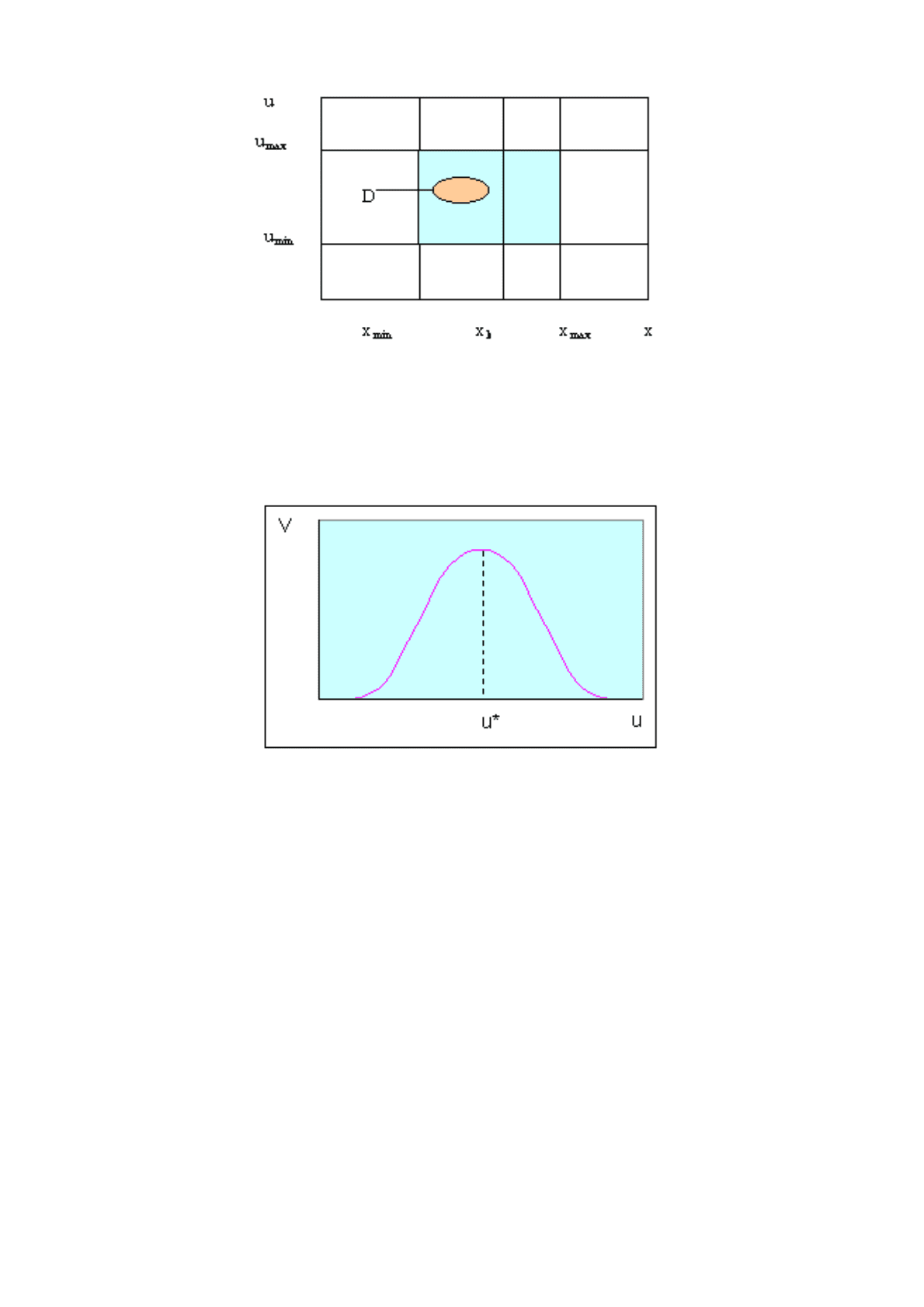
Рис.5.2. Сжатие множества при наличии моделей и взаимосвязей между параметрами.

3. Наличие локальных устройств автоматики на объекте при наличии в соответствующей

задаче критерия оптимальности Vдает возможность сжать множество управляемых и

контролируемых параметров и множество моментов времени, т.е. перейти от непрерывного к

дискретному управлению (рис.5.3).

Рис.5.3. Сжатие множества при наличии у элементов системы критерия V.

В задаче децентрализованного управления в качестве алгоритма, сжимающего множество

возможных состояний системы во времени, может применяться задача слежения [230]. Под

слежением понимается использование замкнутого регулятора, который принуждает состояние

системы х(t) или ее выход y(t) следовать заданному переменному координирующему сигналу

(t) или y

(t). В случае, когда координирующие сигналы изменяются лишь время от времени,

являясь кусочно-постоянными, задача слежения превращается в задачу регулирования.

Следящая система или регулятор выполняют свою основную функцию с минимизацией

некоторого критерия качества V (интеграл квадрата ошибки, затраты энергии и т.д.).

Следует выделить следующие основные типы декомпозиции в решении проблемы управления

сложными распределенными системами [294, 341]:

Функциональная декомпозиция

, при которой задача управления заменяется на

совокупность взаимосвязанных или отдельных подзадач с учетом функций, выполняемых

отдельными подсистемами. Так, например, для системы с распределенными параметрами

система дифференциальных уравнений в частных производных декомпозируется в несколько

дифференциальных уравнений в частных производных.

Пространственная декомпозиция

, которая расчленяет пространственную область на

несколько подобластей и пол

чает соответств

ющ

ю математическ

ю декомпозицию. После

проведения функциональной декомпозиции каждая подзадача может быть далее

декомпозирована с привлечением пространственной декомпозиции для получения численного

ешения.

Декомпозиция по времени

, в результате которой для каждого иерархического уровня

определяется периодичность решения соответствующих подзадач, опроса датчиков и ЭВМ

каждого уровня управления. Определение периодичности решения задач и опроса датчиков

может быть осуществлено как на основе теоремы Котельникова [59, 137], так и в виде

адаптивного автоматизированного метода дискретизации [300], основанного на минимизации

интегрального квадратического критерия ошибки.

Процедуры декомпозиции для сжатых множеств.

Для декомпозиции задач можно выделить шесть основных процедур декомпозиции,

доказательства которых с использованием теории сжатых множеств приводятся в работе

[344]: разделение, параметрическая декомпозиция, структурная декомпозиция,

преобразование переменных, преобразование Лагранжа, развитие задачи.

Приведем в целях простоты все эти процедуры для декомпозиции задачи управления на две

подзадачи. Для обобщения этих процедур на любую размерность в работе [344] приводятся

соответствующие многомерные декомпозиционные теоремы.

Разделение

Эта операция заключается в прямой декомпозиции задачи на подзадачи, что является

возможным только в случае выделения подмножества переменных, которые могут изменяться

независимо от других переменных.

Если

и , , ,

где ; ,

сохраняет строгую упорядоченность множества , т.е.

тогда

Параметрическая декомпозиция

. Для этой процедуры производится декомпозиция общей

задачи управления на подзадачи, связанные между собой путем временной фиксации

значений некоторых переменных. Эти переменные называются параметрами и они

обеспечивают взаимосвязь между подзадачами. За счет итерационного взаимодействия между

подзадачами обеспечивается достижение оптимальности решения глобальной задачи

авления.

Если ;

;

и , ,

где ;

тогда

В случае, когда

; .

Структурная декомпозиция

Используя ту же систему обозначений, что и для предыдущих принципов декомпозиции,

процедуру структурной декомпозиции можно записать следующим образом:

где ;

; ; .

Эта процедура определяет лишь вид получаемых подзадач, но не дает конструктивных

методов построения .

Преобразование переменных

. Задача может быть преобразована в эквивалентную задачу

введением новых переменных, которые связаны с начальными переменными. Если

и и ,

где , тогда

Преобразование Лагранжа

. Путем введения множителей Лагранжа упрощается система

ограничений за счет введения дополнительных отношений и переменных в целевую

фу

нкцию.

Если

и ,

где есть - мерное Евклидово пространство, - размерность , и лагранжиан

определяется как

причем существует седловая точка , тогда

где означает проекцию вдоль

на

, а

Существование седловой точки можно проверить, воспользовавшись процедурой

параметрической декомпозиции для построения следующим образом:

; ,

где и

Функция часто называется двойственной функцией, и с ее

помощью можно проверить,

является ли полученное решение седловой точкой с помощью теоремы

двойственности [344], которая формулируется следующим образом:

Точка является седловой точкой лагранжиана тогда и только тогда, когда

Кроме возможности проверки, является ли точка седловой, теорема двойственности может

использоваться для оценки сходимости итерационного алгоритма, используемого для

вычисления . Если на k-ой итерации ,

тогда находится внутри

- окрестности .

Развитие задачи

. При решении сложных производственных задач иногда необходимо

бывает преобразовывать задачу в другую задачу, не точно эквивалентную исходной. Таким

образом можно применять различные типы аппроксимаций, вводить упрощения в исходную

задачу, отбрасывая несущественные переменные с уточнением отдельных деталей задачи

[344]. Развитие задачи используется также и при наличии неопределенных факторов в задаче.

Для строгого определения этой операции необходимо характеризовать исходную задачу

таким об

азом, чтобы

мализовать неполнот

, неточность этой задачи.

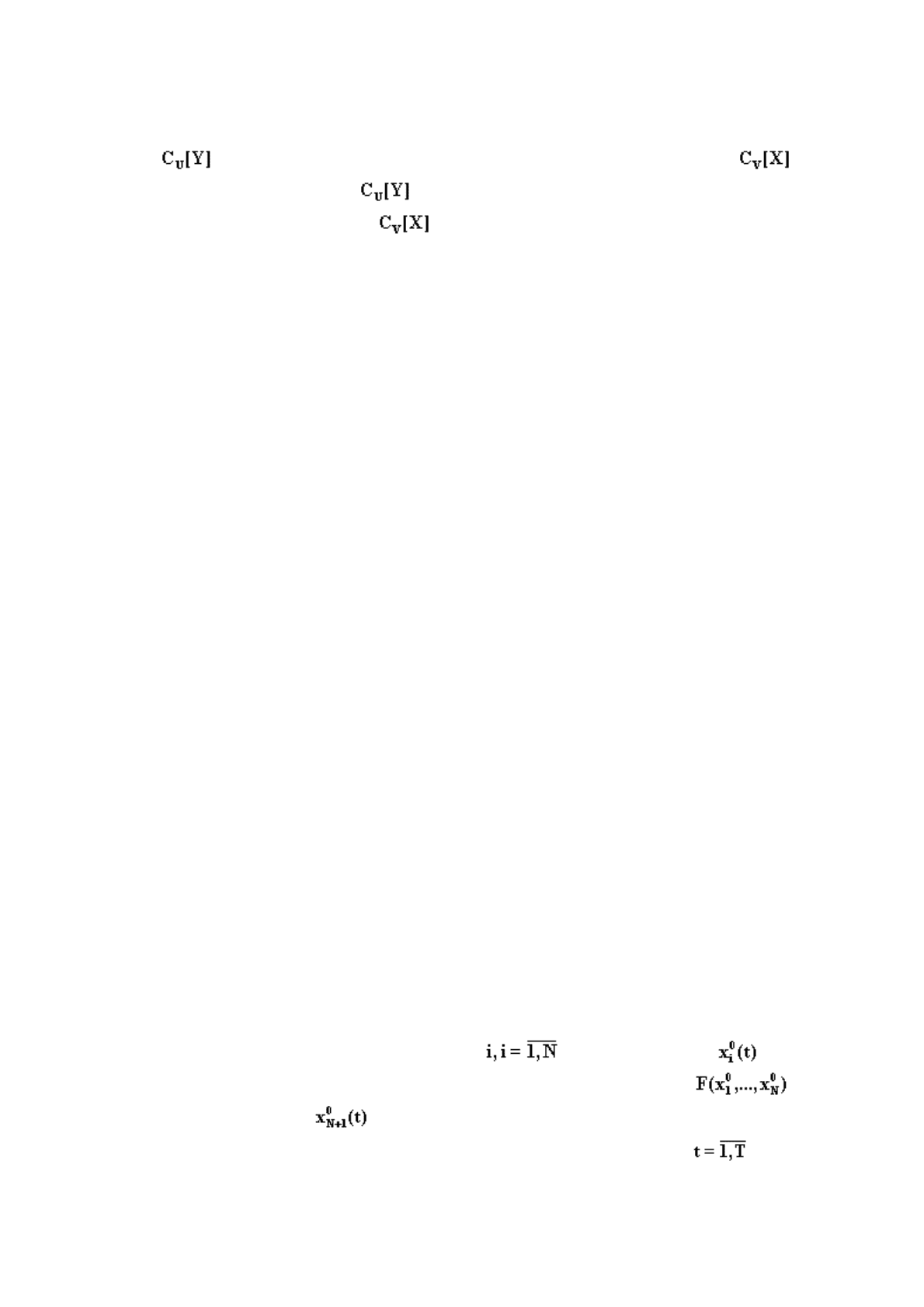
Это может быть достигнуто путем введения допущения, что задача является неполной и

сжатое множество является нечетким множеством за счет того, что ограничения или целевая

функция V являются нечеткими. Процедура развития задачи вводится в [344] следующим

образом: является приемлемым развитием нечеткого сжатого множества тогд

и только тогда, когда все члены с высокой степенью принадлежности также имеют

высокую степень принадлежности в .

Процедуры (1)-(3) обеспечивают различные разбиения задач на подзадачи. Первая - разделяет

задачу на независимые подзадачи, а две другие осуществляют декомпозицию на

взаимодействующие подзадачи. Процедуры (4)-(6) производят преобразование задачи.

Причем процедура развития задачи добавлена для распространения теории декомпозиции на

генерацию иерархических структур и на учет неопределенности в системе (развитие задачи с

целью учета неточных, либо отсутствующих данных). То есть, в частном случае процедура

преобразования может осуществлять и расширение вектора переменных до нового вектора

большей размерности. В процессе декомпозиции задачи появляются новые решающие блоки,

цель которых - оценивание приемлемости принятых допущений в зависимости от ситуации.

Декомпозиция сложной задачи обычно осуществляется путем использования комбинации

приведенных выше процедур декомпозиции.

Однако определенные в результате проведения декомпозиции задачи могут быть сильно

связаны между собой и итерационный процесс получения согласованного решения может

быть очень длительным и обладать плохой сходимостью. Поэтому для получения

иерархической структуры задач принятия решения возникает необходимость проведения

процедуры развития отдельных задач, т.е. некоторые подзадачи могут дублироваться и

ешаться в составе задач разных уровней управления. Эти подзадачи не будут полностью

идентичными и должны отличаться различными допущениями, например, в подзадаче

вышестоящего уровня управления в отличие от сложного нестационарного расчета режима

транспорта газа в задаче нижестоящего уровня могут игнорироваться высокочастотные

возмущения, использоваться меньшая периодичность решения и получения данных,

применяться упрощенная эквивалентная расчетная схема газопровода. Однако получаемые

ешения должны быть эквивалентными в рамках заданной погрешности.

5.4. Координация нечетких решений в многоуровневой

иерархической системе

Процедура соединения элементов в многоуровневой иерархической системе может быть

сведена к некоторой рекуррентной процедуре. Рассмотрим построение этой рекуррентной

процедуры, основываясь на работе [54]. Этот алгоритм относится к классу безытеративных

алгоритмов.

При принятии оперативных решений в сложной иерархической системе (рис.5.4) основной

целью является нахождение на каждом уровне вектора решений , которые

обеспечивают максимум системного вектора

целевых функций при

координационном задании , полученном от (N+1)- о уровня управления. Причем

процесс принятия решений осуществляется дискретно в моменты времени и в общем

случае, шаг дискретизации по управлению возрастает от нижних уровней к верхним. Часть

ешений

(

в основном на нижних

ур

овнях

)

носит ха

акте

авляющих воздействий,