Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях
Подождите немного. Документ загружается.


Т
(
Возраст
) =
молодой +
старый
+
не молодой
+
не старый
+
+
не молодой и
не старый
+
очень молодой
+
очень старый
+ ... (4.26)
Если отождествить союз
и
с операцией пересечения,
или
- с операцией объединения,
отрицание
не
с операцией взятия дополнения и модификатор
очень
- с операцией
концентрации, то можно записать смысл типичного значения переменной
Возраст
. Например:
М
(
не молодой
) =
молодой
,
М
(
не очень молодой
) = (
молодой
2
), (4.27)
М
(
не очень молодой и не очень старый
) = (
молодой
2
)
Χ
(
старый
2
).
Эти уравнения выражают, по сути дела, смысл составного терма как функцию смысла
составляющих его первичных термов.
Более общий подход базируется на определении семантики контекстно-свободных языков.
Например, можно проверить, что терм-множество (4.26) порождается контекстно-свободной
грамматикой , в которой
нетерминальные символы
(
синтаксические
категории
) обозначаются
V
N
= T + A + B + C + D + E
, (4.28)
в то время как множество
терминальных символов
(компоненты термов в
Т
) выражаются в
виде
V
T
=
молодой +
старый
+ очень + не + и + или +
( ), (4.29)
а система подстановок
P
имеет вид
Т
→
A
,
Т
→
T
или
A
,
A
→
B
,
A
→
A
и
B
,
B
→
C
,
B
→
не
C
,
C
→
(
T
),
C
→
D
,
C
→
E
,
D
→
очень
D
,
E
→
очень
E
,
D
→
молодой
,
E
→
старый
. (4.30)
Систему
P
можно представить алгебраически в виде следующей системы уравнений:
Т
=
A
+
Т
или
A
,
A
=
B
+
A
и
B
,
B
=
C
+
не
С
, (4..31)
C
= (
T
) +
D
+
E
,
D
=
очень
D
+
молодой
,
E
=
очень
E
+
старый
.
Решение этой системы уравнений относительно
Т
является терм-множество
Т
, описываемое
вы
р
ажением
(
4.26
)
. Решение системы
(
4.31
)
можно пол
у
чить ите
р
ативно, использ
у
я
соответствующие рекуррентные соотношения. Итерирование порождает все больше и больше
термов в каждой из синтаксических категорий (
T,A,B,C,D,E
).
В более общепринятой процедуре терм в
Т
, скажем,
не молодой и не старый
порождается
грамматикой
G
путем последовательных замен (подстановок) с использованием системы
P
,
причем каждая цепочка подстановок начинается с
Т
и заканчивается этим термом:
T
→
A
→
A
и
B
→
B
и
B
→
не
C
и
B
→
не
C
и не
C
→
не
D
и не
C
→
→
не
D
и не
E
→
не молодой и не
E
→
не молодой и не старый
. (4.32)
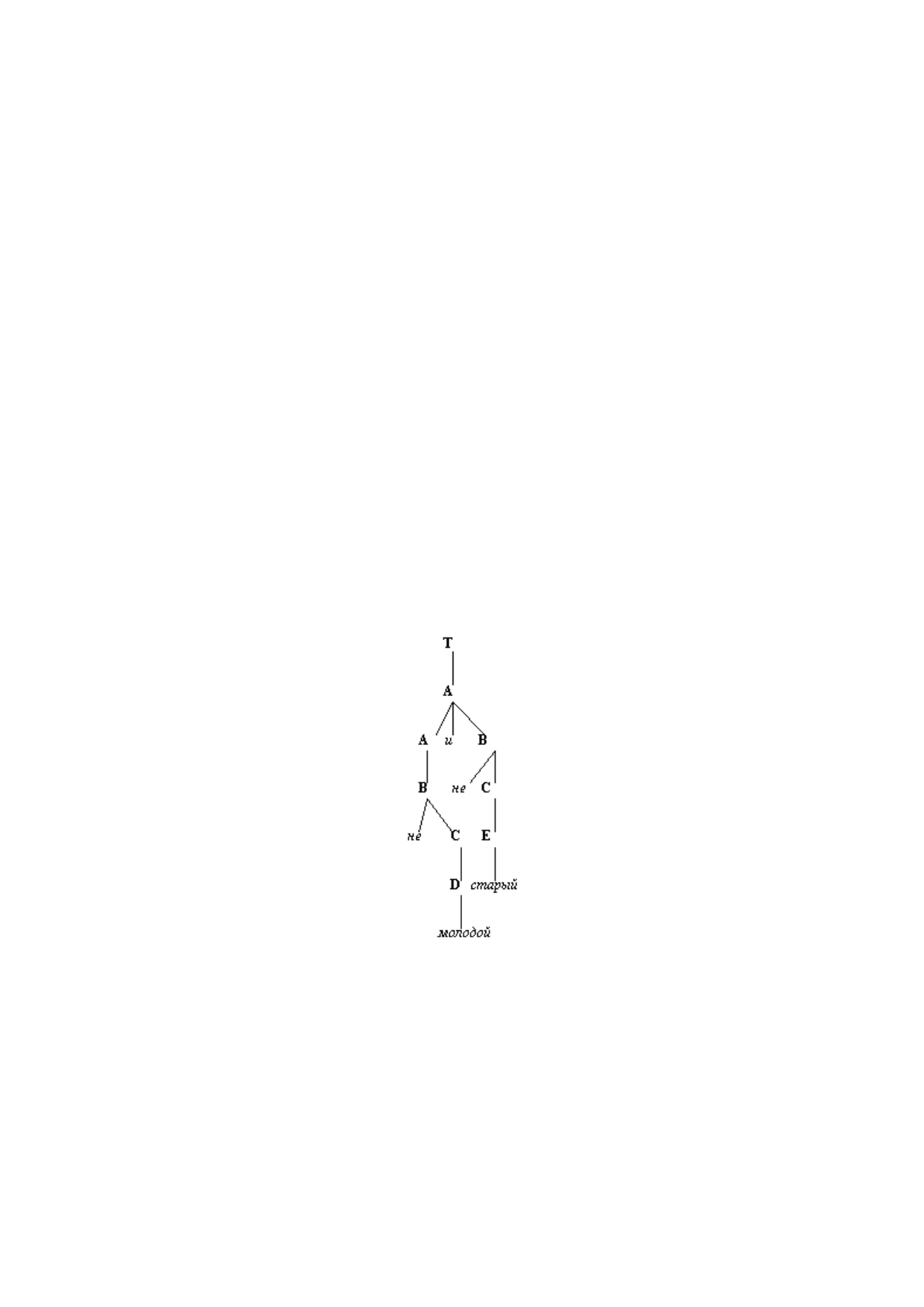
Эту цепочку можно получить, используя синтаксическое дерево (рис. 4.8), представляющее
структуру терма
не молодой и не старый
с использованием синтаксических категорий
T,A,B,C,D,E
. Описанная процедура порождения термов в
Т
грамматикой
G
в сущности
составляет
синтаксическое правило
для переменной
Возраст
.
Семантическое правило
для переменной
Возраст
индуцируется описанным выше
синтаксическим правилом, так как смысл терма в
Т
частично определяется его
синтаксическим деревом.
В частности, каждому правилу подстановки ставится в соответствие некоторое отношение
между нечеткими множествами, обозначенные определенными терминальными и
нетерминальными символами. Эта двойственная система подстановок и связанных с ней
уравнений типа (4.27) используется для вычисления смысла составных термов из
Т
следующим образом.
Рис. 4.8. Синтаксическое дерево для значения
не молодой и не старый
.
1. Рассматриваемый терм подвергается грамматическому разбору, в результате чего
получается синтаксическое дерево. Конечными вершинами этого дерева являются:
а) первичные термы, смысл которых определяется априори,
б) названия модификаторов (т.е. лингвистических неопределенностей, союзов, отрицания и
т.п.),
в) маркеры, такие, как скобки, которые облегчают грамматический разбор.
2. Пе
р
вичным те
р
мам на конечных ве
р
шинах де
р
ева назначается их смысл и затем с помощью
системы подстановок
Р
и соответствующих уравнений вычисляется смысл ближайших к ним
нетерминальных символов.
3. После этого дерево урезают так, чтобы вычисленные терминальные символы оказались
конечными вершинами оставшегося поддерева.
Этот процесс повторяется до тех пор, пока не будет вычислен смысл терма,
соответствующего корню исходного синтаксического дерева. Основное назначение
описанной процедуры состоит в том, чтобы связать смысл составного терма со смыслом
составляющих его первичных термов посредством системы уравнений, определяемой
грамматикой, порождающей термы в
Т
.
4.5. Нечеткие условные предложения и составное правило
вывода
Возможность определять смысл значений, принимаемых лингвистической переменной,
необходима для анализа неопределенных высказываний вида "если
А
, тогда
В
". Например,
если
х
-
большой
, тогда
у
-
малый
,
если дорога
скользкая
, тогда езда
опасная
.
В сущности предложения этого вида описывают отношения между двумя нечеткими
переменными. Это означает, что такие высказывания следует определять как нечеткое
отношение на декартовом произведении множеств.
Пусть
А
- нечеткое подмножество области рассуждения
Х
, а
В
- нечеткое подмножество
другой, вообще говоря, области рассуждения
Y
. Рассмотрим простой пример:
Х
= 1 + 2
Y
= 1 + 2 + 3
А
= 1/1 +0,8/2
B
= 0,6/1 + 0,9/2 +1/3
Тогда
А
∗
В
= 0,6(1,1) + 0,9(1,2) + 1(1,3) + 0,6(2,1) + 0,8(2,2) + 0,8(2,3). (4.33)
Данное отношение можно представить матрицей отношения:
Смысл нечеткого высказывания вида "если
А
, тогда
В
" становится более ясным, если
р
ассматривать его как специальный случай условного высказывания "если
А
, тогда
В
, иначе
С
". В терминах декартова произведения последнее предложение определяется так:
А
∗
В
(
А
∗
С
)
(
4.34
)
1 2 3
1 0,6 0,9 1
2 0,6 0,8 0,8

Если предположить, что
С = У
, то получаем:
А
∗
В ( А
∗
Y)
(4.35)
Последнее означает, что в отсутствие указаний к противному
С
может соответствовать
любому нечеткому подмножеству области рассуждения, т.е. высказывание "если
А
, тогда
В
"
интерпретируется высказыванием "если
А
, тогда
В
, иначе
безразлично
".
Для нашего примера
( А
∗
Y)
определяется матрицей отношения
(4.36)
Подставляя матрицы (4.33, 4.36) в (4.35) находим, что матрица отношения "если
А
, тогда
В
" в
нашем примере имеет вид матрицы
А
∗
В
(4.33).
Если допустить, что
С
пустое множество , а не
Y
, то (4.34) сведется к декартовому
произведению
А
∗
В
.
Полезно учитывать, что в терминах матриц отношения равенство (4.34) можно выразить как
сумму попарных произведений,
содержащих
А
и
В
или
А
и
С
в виде вектор-столбца и
вектор-строки соответственно. Так,
если
А
, тогда
В
, иначе
С = [А][В] + [ А][С]
.
Рассмотрим следующий пример. Предположим, что
X
=
Y
= 1 + 2 + 3,
А
=
малый
= 1/1 + 0,4/2,
В
=
большой
= 0,4/2 + 1/3, (4.37)
С
=
не большой
= 1/1 + 0,6/2.
Тогда если
А
, тогда
В
, иначе
С
= (1/1 + 0,4/2)
∗
(0,4/2 + 1/3) + (0,6/2 + 1/3)
∗
(1/1 + 0,6/2) =
= 0,4(1,2)+1(1,3)+0,4(2,2)+0,4(2,3)+0,6(2,1)+0,6(2,2)+1(3,1)+0,6(3,2),
что можно представить в виде матрицы отношения
(4.38)
Аналогично,
1 2 3
1 0 0 0
2 0,2 0,2 0,2
0 0,4 1
0,6 0,6 0,4
1 0,6 0
если
А
, тогда
В
= (1/1 + 0,4/2)
∗
(0,4/2 + 1/3) + (0,6/2 + 1/3)
∗
(1/1 + 1/2 + 1/3) =
= 0,4(1,2) + 1(1,3) + 0,4(2,2) + 0,4(2,3) + 0,6(2,1) + 0,6(2,2) + 0,6(2,3)+
+ 1(3,1) + 1(3,2) + 1(3,3),
что эквивалентно матрице отношения
(4.39)
Пример 4.2.
Заданы универсальные множества
X
=
Y
= 1 + 2 + 3 и нечеткие множества:
А
=
малый
= 1/1 + 0,4/2,
В
=
большой
= 0,4/2 + 1/3,
1. Определить матрицу отношения
R
= если
А
, то
В
, иначе
С
,
где
С
=
не очень большой
.
2. Найти результат композиции термина
очень малый
и отношения
R
.
С
=
не большой
= 1/1 + 0,84/2.
Матрица отношения
А
∗
В
:
Матрица отношения
А
∗
С
:
Тогда матрица - если
А
, то
В
, иначе
С
:
Результат композиции
очень малый
с
R
есть:
Пусть термины
малый
и
большой
определены соответственно как
м
аленький
= 1/1 + 0,8/2 + 0,6/3 + 0,4/4 + 0,2/5,
0 0,4 1
0,6 0,6 0,6
1 1 1
0 0,4 1
0 0,4 0,4
0 0 0
0 0 0
0,6 0,6 0
1 0,84 0
0 0,4 1
0,6 0,6 0,4
1 0,84 0
0,16 0,4 1
большой
= 0,2/1 + 0,4/2 + 0,6/3 + 0,8/4 + 1/5.
Тогда, подставляя в (4.33)
малый
вместо А,
большой
вместо В, получаем матрицу отношения
А
∗
В
:
Далее, подставляя
не очень большой
вместо С, получаем матрицу отношения
А
∗
С
:
Матрица отношения R получаем путем объединения
А
∗
В ( А
∗
С)
:
Результат композиции R с х есть
очень малый
:
Вообще, если - нечеткие подмножества
Х
, а - нечеткие подмножества из
Y
, то
если , тогда , иначе, . . . , если , тогда =
= (4.40)
Последнее выражение переходит в предыдущее, если выражение "если
А
, тогда
В
, иначе
С
"
интерпретировать как "если
А
, тогда
В
, иначе если
А
, тогда
С
".
4.6. Простые отношения между нечеткими переменными
При традиционном подходе зависимость между числовыми переменными
х
и
у
часто
описывают с помощью таблицы, которую словесно можно представить в виде набора
высказываний типа "если
х
равно 5, то
у
равно 10" и т.д. Такой же способ описания
п
р
именяется и для нечетких пе
р
еменных. В частности, если
х
и
у
- лингвистические
0,2 0,4 0,6 0,8 1
1
0,2 0,4 0,6 0,8 1
0,8
0,2 0,4 0,6 0,8 0,8
0,6
0,2 0,4 0,6 0,6 0,6
0,4
0,2 0,4 0,4 0,4 0,4
0,2
0,2 0,2 0,2 0,2 0,2
0,96 0,84 0,64 0,36 0
0
0 0 0 0 0
0,2
0,2 0,2 0,2 0,2 0
0,4
0,4 0,4 0,4 0,36 0
0,6
0,6 0,6 0,6 0,36 0
0,8
0,8 0,8 0,64 0,36 0
0,2 0,4 0,6 0,8 1
0,2 0,4 0,6 0,8 0,8
0,4 0,4 0,6 0,6 0,6
0,6 0,6 0,6 0,4 0,4
0,8 0,8 0,64 0,36 0,2
0,36 0,4 0,6 0,8 1
переменные, то используются высказывания вида "если
А
, то
В
", где
А
и
В
- символы
нечетких множеств, представляющие собой значения переменных
х
и
у
. Например:
если
х
мало
, то
у
велико
;
если
х
не мало
, то
у
не очень велико
и т.д.
Следует заметить, что выражение типа "если
А
, то
В
" можно использовать для представления
нечеткого графика как объединение нечетких точек, если, например, положить
А
i
=
близко к
х
i,
, В
i
=
близко к
y
i
, i=1,...,n
,
где
х
i
и
y
i
- точки на оси
Х
и
Y
соответственно.
Нечеткие высказывания играют основную роль в нечетких алгоритмах. Типичная проблема, с
которой сталкиваются при разработке таких алгоритмов, состоит в следующем. Имеется
нечеткое отношение
R
в
X
∗
Y
, которое определяется нечеткими высказываниями. Проблема
состоит в том, чтобы для любого нечеткого подмножества
х Х
определить нечеткое
подмножество
y Y
, которое
х
индуцирует в
Y
. Например, пусть имеются следующие два
предложения:
1.
х
-
очень малый
,
2. если
х
-
малый
, тогда
у
-
большой
, иначе
у
-
не очень большой
.
Возникает вопрос: какова будет величина
у
, если
х
очень мал
?
Ответ на этот вопрос дается
композиционным правилом вывода
: Если
R
- неопределенное
отношение
X
↔
Y
и
х
-нечеткое подмножество
Х
, тогда нечеткое подмножество
y Y
, которое
индуцируется подмножеством
х
, определяется композицией
R
и
х
, т.е.
у = х
°
R
,
где
х
играет роль унарного отношения.
Композиционное правило вывода - это всего лишь обобщение следующей известной
процедуры. Предположим, что имеется кривая
y = f(x)
и задано значение
х = a
. Тогда из этого
мы можем заключить, что
y = f(x) = b
.
Обобщим теперь этот процесс, предположив, что
а
- интервал, а
f(x)
- функция, значения
кото
р
ой с
у
ть инте
р
валы
(
р
ис.4.9
)
.

Рис.4.9. Композиционное правило вывода в случае интервальных переменных.
В этом случае, чтобы найти интервал
y = b
, соответствующий интервалу
а
, построим сначала
цилиндрическое множество с основанием
а
и найдем его пересечение с интервальным
графиком. Затем спроектируем это пересечение на ось
Y
и получим желаемое значение
y
в
виде интервала
b
.
Пусть теперь
А
- нечеткое множество оси
Х
, а
F
- нечеткое отношение в
Х
∗
Y
. Образуем
цилиндрическое нечеткое множество
⎯
А
с основанием
А
:
Пересекаем его с нечетким отношением
F
и проектируем затем это пересечение на ось
Y
.
Таким образом получаем значение у в виде нечеткого подмножества оси
Y
:
. (4.41)
Сравнивая это выражение с определением композиции, можно заметить, что
B =A
°
F
, (4.42)
где знак
°
- обозначает операцию композиции.
Если нечеткие множества
A
и
F
имеют конечные носители, то операция композиции сводится
к максиминному произведению матриц.
В качестве иллюстрации приведем простой пример. Допустим, что
X
=
Y
= 1 + 2 + 3 + 4,
А
=
малый
= 1/1 + 0,6/2 + 0,2/3,
F
=
примерно равны
= 1/((1,1) + (2,2) + (3,3) +(4,4)) +
0,5/((1,2) +(2,1)+ (2,3) + (3,2) + (3,4) + (4,3))
Следовательно,
В
=
малый
°
примерно равны =
Полученный результат можно аппроксимировать как
более или менее малый
.
Пусть, например, матрица отношения "если
х
-
малый
, тогда
у
-
большой
, иначе
у
-
не
большой
" имеет вид (13.6). Тогда, полагая
х
равным
более или менее малый
= 1/1 + 0,4/2 + 0,2/3,
получаем
более или менее малый
°
(если
х
-
малый
, тогда
у
-
большой
, иначе
у
-
не большой
) =
Грубым приближением результата может быть
более или менее большой
.
Из-за использования максиминного произведения матриц отношение между
х
и
у
не
непрерывно, т.е. малое изменение
х
не произведет изменения в
у
, пока не будет превышен
некоторый порог. Этого не будет в случае, если композиция
х
и
R
определена с помощью
max
-произведения.
Следует заметить также, что когда
х = А
, мы получим
у = А
°
R = В
, что строго выполняется,
когда
А, В
и
С
- обычные множества, и приближенно, когда
А, В
и
С
- нечеткие множества.
Ч
ем больше
х
отличается от
А
, тем менее четко определен
у
. Дополнительный источник
неточности связан с представлением нечеткого множества как значения лингвистической
переменной (см. предыдущий пример).
4.7. Нечеткие алгоритмы
Для описания более сложных зависимостей
у
от
х
используются нечеткие алгоритмы.
Н
ечеткий алгоритм есть
у
порядоченное множество нечетких инстр
у
кций
, которые при
их реализации дают приближенное решение проблемы. Инструкции в нечетких алгоритмах
можно разделить на три класса:
1.
Назначающие предложения
, например,
х
=
большой.
2.
Нечеткие высказывания
типа "если
А
, тогда
В
". В таких предложениях либо первое
условие, либо второе, либо оба могут быть символами нечетких множеств.
3.
Б
ез
у
словные активные п
р
едложения
, нап
р
име
р
,
1 0,5 0 0
1 0,6 0,2 0
°
0,5 1 0,5 0 = 1 0,6 0,5 0,2
0 0,5 1 0,5
0 0 0,5 1
0 0,4 1
1 0,4 0,2
°
0,6 0,6 0,4 = 0,4 0,4 1
1 0,6 0

немного
уменьшить
х
,
печать
х
,
стоп.
Некоторые из этих инструкций являются нечеткими, другие - нет.
Комбинировать назначающие и нечеткие высказывания нужно в соответствии с
композиционным правилом вывода. Например, если в некоторый момент выполнения
алгоритма мы встречаем инструкции
1.
х
-
очень малый
,
2. если
х
-
малый
, тогда
у
-
большой
, иначе
у
-
не большой
,
где термины
маленький
и
большой
определяются согласно (4.37),тогда результатом
выполнения этих инструкций будет
очень
малый
= 1/1 + 0,16/2,
Приближением результата может быть терм
более или менее большой
.
Безусловная нечеткая инструкция выполняется аналогично. Например, выполнение
инструкции "умножить
х
само на себя
несколько
раз", где термин "несколько" определен
следующим образом
несколько
= 0,7/1 + 1,0/2 + 1,0/3 + 0,6/4 + 0,2/5,
дает нечеткое множество
у = 0,7/х
2
+ 1,0/х
3
+ 1,0/х
4
+ 0,6/ х
5
+ 0,2/х
6
.
Важно отметить, что как в первом, так и во втором случае результатом выполнения
инструкции является нечеткое множество, а не единственное число. Однако когда человек
дает нечеткую инструкцию, такую, как "сделать
несколько
шагов", то результат выполнения
должен быть единственным числом. Наиболее разумно допустить, что результатом
выполнения будет элемент нечеткого множества, имеющий наивысшую степень
принадлежности этому множеству. Если такой элемент не единственен, то можно сделать
среди них случайный или произвольный выбор. Можно также ввести некоторый критерий,
который линейно упорядочивает элементы, имеющие наивысшую степень принадлежности к
нечеткому множеству, и, таким образом, образуется единственный наибольший элемент.
Аналогичный вопрос возникает, когда нужно ответить "да" или "нет"
на нечеткий вопрос.
Например,
"если
х
-
мало
, тогда стоп, иначе идти к метке".
П
у
сть
малый
= 1/1 + 0,6/2 + 0,2/3.
0 0,4 1
1 0,16 0
°
0,6 0,6 0,6 = 0,16 0,4 1
1 1 1
