Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях

Подождите немного. Документ загружается.

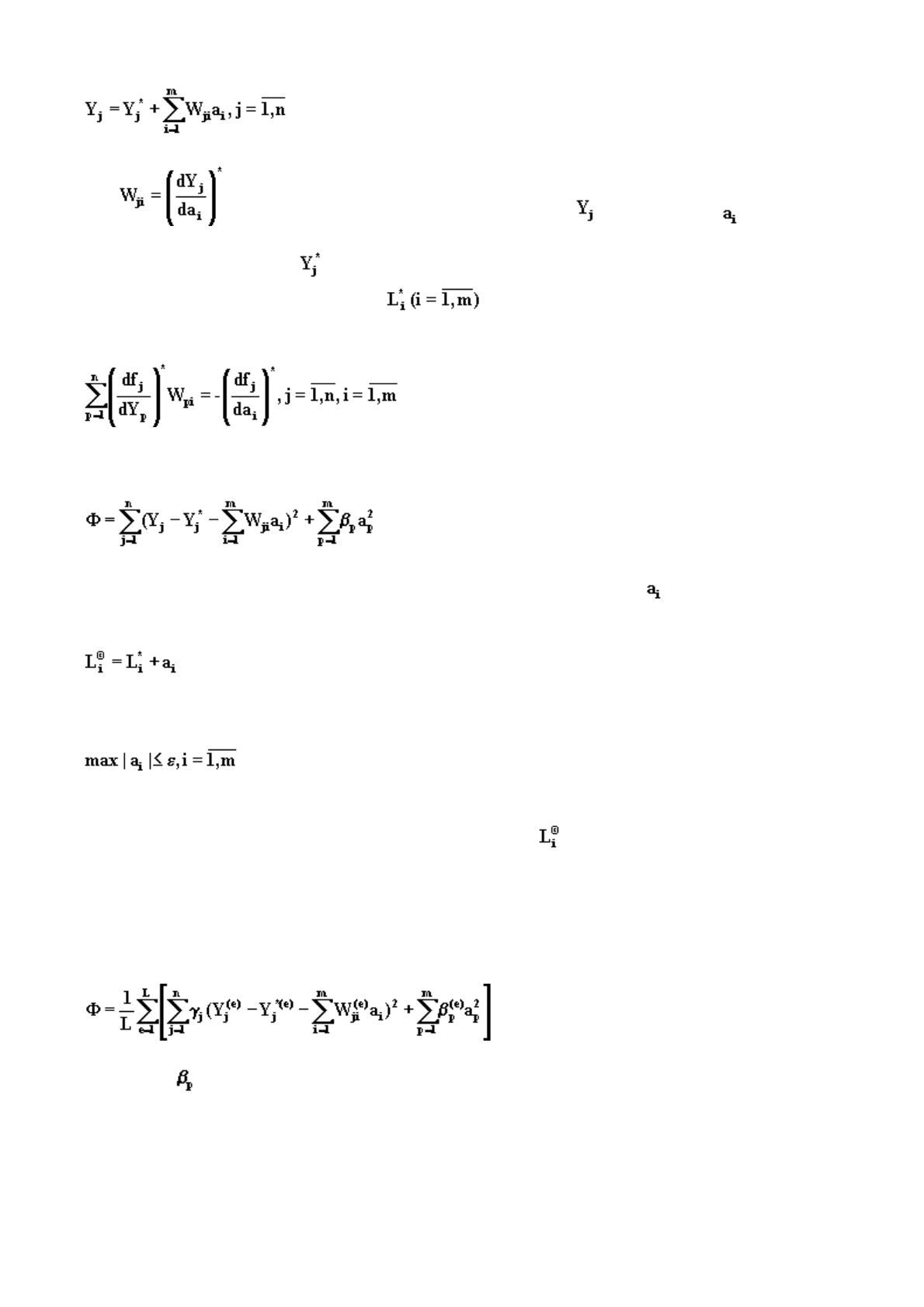
, (6.52)

где - функция чувствительности переменной по параметру , причем * -

означает, что производные или переменные вычисляются при номинальных значениях

параметров. Переменные определяются из решения заданной системы уравнений при

номинальных значениях параметров , а функции чувствительности находятся из

ешения системы линейных уравнений

. (6.53)

Далее из условий минимума квадратической формы вида

(6.54)

находятся по методу наименьших квадратов оценки параметров , а по ним и новые

значения параметров

(6.55)

После этого проверяется критерий окончания счета

, (6.56)

где

- заданная точность оценки параметров. Если условие (6.56) выполняется, то расчет

считается законченным, если нет - полученные оценки принимаются

как номинальные и

асчет повторяется.

Вопросы существования и единственности решения для этого метода обсуждаются в

[108,стр.260]. Этот метод может также применяться и при наличии одновременно L замеров

для всех переменных. В этом случае квадратическая форма Ф выглядит следующим образом:

. (6.57)

Величины определяются с использованием рекомендаций теории чувствительности,

весовые коэффициенты

могут выбираться равными обратным значениям дисперсий

измерений [108]. Конкретные примеры по выбору и приведены для различных задач

газотранспортных сетей в работе [30].

Использование нескольких последовательных заме

ов

ежимов

аботы сети газоп

оводов

приводит к переходу от недоопределенной к переопределенной системе узловых уравнений

[153]. Однако если удастся получить замеры лишь незначительно отличающихся друг от

друга режимов, то это может привести к плохой обусловленности матрицы нормальной

системы уравнений.

Применение сложных нестационарных моделей требует больших дополнительных объемов

исходной информации, которую либо готовит диспетчерский персонал, либо она собирается с

помощью телеметрии.

Однако низкая точность этой дополнительной информации, отсутствие целого ряда

дополнительных датчиков, сложность комплексной проверки вводимой информации

заставляет разработчиков АСДУ искать принципиально новые подходы к моделированию

ежимов, например, использовать функции чувствительности энергосистем [148].

На этих же идеях теории чувствительности построен алгоритм регулирования напряжения и

мощности в энергетических системах иерархической структуры [258]. С использованием

ЭВМ первого уровня иерархии осуществляют регулирование напряжения и мощности в

пределах подсистем в предположении линейной зависимости связывающих отклонения

егулируемых параметров с отклонениями параметров режима регулирующих устройств

с учетом соответствующих матриц чувствительности S

, (6.58)

где - отклонения параметров, вызванные изменениями нагрузок. ЭВМ вышестоящего

уровня осуществляет координацию потоков с учетом связей отдельных подсистем.

Накопленный в электроэнергетике опыт показывает эффективность и достаточную точность

анализа чувствительности при решении задач диспетчерского управления режимами и

связанных с ними оптимизационных проблем [150]. Представленный в работах Тиннея В.Ф. и

Доммела Г.В. [150] обобщенный метод для вычисления чувствительности одной или

нескольких зависимых переменных или некоторой целевой функции к изменению некоторого

подмножества специально выбранных параметров электроэнергетической системы,

использует линейное приближение и в условиях нормальных режимов является достаточно

точным. Однако даже в условиях, значительно отличающихся от нормальных, знак и

величина коэффициентов чувствительности могут оказаться полезной информацией,

указывающей на признаки аварийной ситуации [150]. Для улучшения сходимости могут

использоваться понятия нечеткой чувствительности при наличии нечетко заданных замеров и

коэффициентов уравнений [170].

6.3. Игры в нечетко определенной обстановке

Во многих прикладных областях часто встречаются ситуации, в которых выполнение цели

или результаты принятия решений одним лицом зависят не только от его действий, но и от

действий другого лица или группы лиц, преследующих свои собственные цели.

Рассмотренный подход к задачам принятия решений можно применять и для анализа

подобных игровых ситуаций в нечетко определенной обстановке. Формулируется такая игра

следующим образом.

Пусть

- множества элементов, которые могут выбирать игроки 1 и 2 соответственно.

Допустимые выборы (стратегии) игроков 1 и 2 описываются нечеткими множествами

соответственно с

фу

нкциями п

инадлежности и . Заданы также

фу

нкции

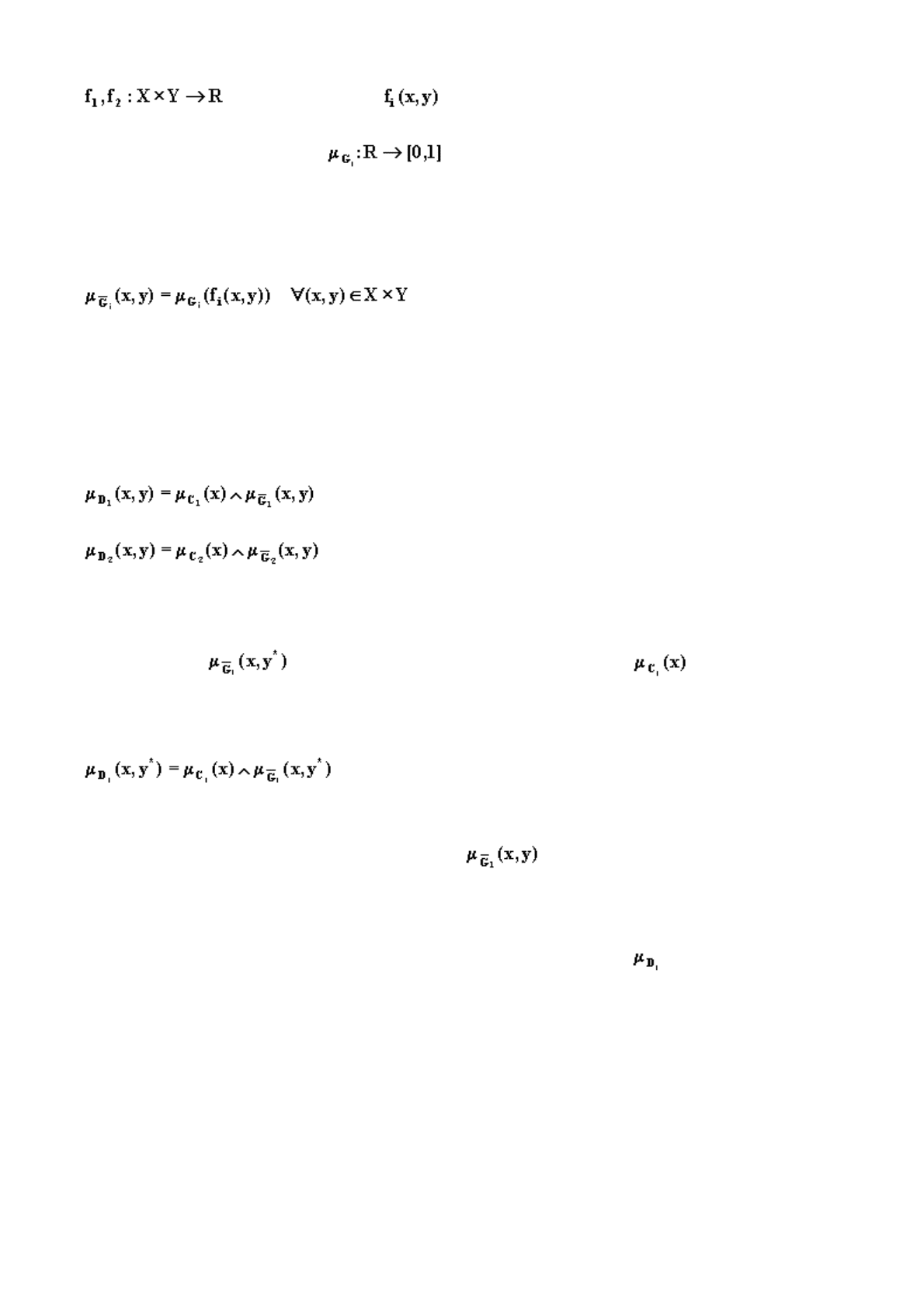
, причем значение есть оценка игроком

ситуации

(х,у)

без учета

допустимости выборов

. Цель игрока

описывается нечетким множеством

функцией принадлежности . Следует заметить, что цель, поставленная

игроком, может оказаться плохо или вообще несовместимой с его возможностями, т.е. с

множеством его стратегий.

Целью игрока

можно считать нечеткое множество в

∗

с функцией принадлежности

. (6.59)

Образом этого нечеткого множества при отображении

вляется заданное нечеткое

множество цели игрока

Введем нечеткие множества

∗

, определив их функции принадлежности

следующим образом:

(6.60)

Смысл нечетких множеств

можно пояснить следующим образом. Если, например,

игроку 1, известен конкретный выбор

игроком 2, то перед ним стоит задача достижения

нечеткой цели при множестве допустимых альтернатив . В соответствии с

используемым здесь подходом Беллмана - Заде решение

такой задачи определяется как

пересечение нечетких множеств цели и ограничения:

. (6.61)

Таким образом, нечеткое множество

можно рассматривать как семейство (по параметру

)

ешений задач достижения нечетких целей . Аналогичный смысл придается и

множеству

Далее будем считать, что при каждом фиксированном выборе одного игрока второй выбирает

стратегию, которая максимизирует соответствующую ему функцию .

Если игрок полагается целиком лишь на свои возможности, то естественной является его

ориентация на получение

наибольшего гарантированного выигрыша

, т.е. рациональным

считается такой способ оценки игроком 1 своих выборов, при котором он рассчитывает на

наихудшую для него реакцию игрока 2 из множества возможных реакций последнего.

При этом важную роль играет имеющаяся в его распоряжении информация об интересах и

ограничениях игрока 2. Если, например, игрок 1 имеет возможность первым выбрать свою

стратегию, а игроку 2 становится известным этот выбор, то наибольший гарантированный

выиг

ыш иг

ока 1

авен

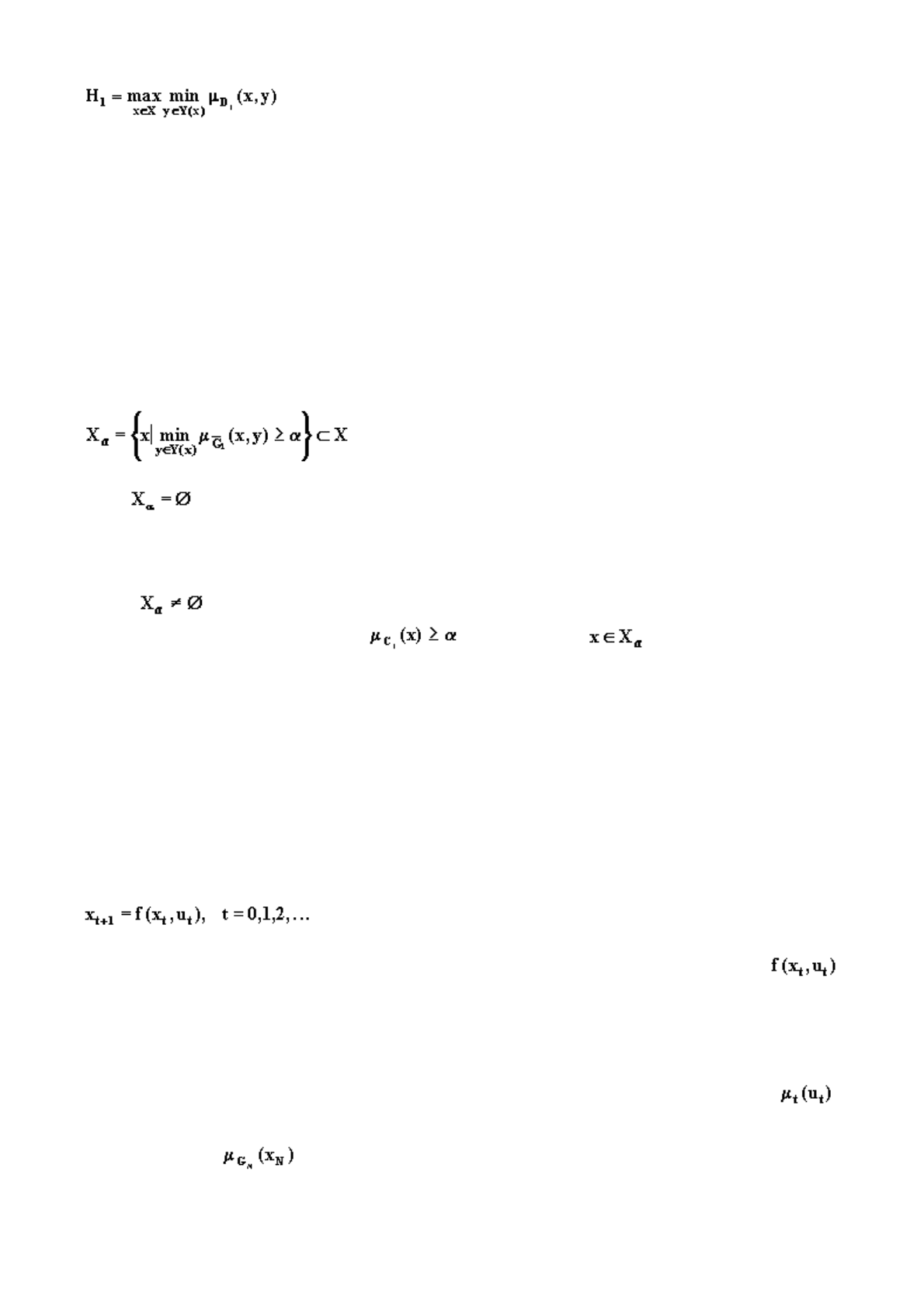
(6.62)

Присутствующее в этом выражении множества

Y(x)

, зависящего от

, есть множество

возможных реакций (ответов) игрока 2 на выбор

игрока 1. В этом смысле зависимость

Y(x)

отражает степень информированности игрока 1 об интересах и ограничениях игрока 2.

Если величина

слишком мала, то это означает, что цель, к выполнению которой стремится

игрок 1, слишком завышена (с учетом его возможностей). В связи с этим естественным

образом возникает следующая задача. Каково должно быть нечеткое множество стратегий

игрока 1, которое гарантировало бы ему (при заданной информированности об игроке 2)

достижение цели со степенью, не меньшей некоторого заданного числа

Для решения этой задачи введем множество

(6.63)

Если , то

, и следовательно, игрок 1 не может гарантировать достижение своей

цели со степенью большей или равной

независимо от того, какое множество стратегий

находится в его распоряжении.

Пусть , тогда можно заключить, что гарантировать достижение цели со степенью не

менее

можно только тогда, когда при некотором .

6.4. Многошаговые процессы принятия решений

Для простоты будем полагать, что управляемая система

является инвариантной по времени

детерминированной системой с конечным числом состояний. Именно, каждое состояние

, в

котором система

находится в момент времени

t, t=0,1,2,...

, принадлежит заданному

конечному множеству возможных состояний

Х= {

,...,

}

; при этом входной сигнал в

момент времени

является элементом множества

U={

,...,

}

. Динамика системы во

времени описывается уравнением состояния

, (6.64)

в котором

- заданная функция, отображающая

∗

. Таким образом,

представляет собой последующее состояние для

при входном сигнале

. Считается также,

что заданы начальное состояние

и фиксированное время окончание процесса

Предполагается, что в каждый момент времени

на входную переменную наложено нечеткое

ограничение

, являющееся нечетким множеством в

с функцией принадлежности .

Кроме того, считается, что цель - нечеткое множество

, определяемое функцией

принадлежности . Задача заключается в нахождении максимизирующего решения.

Использ

я идеи п.5.1, можно записать

ешение как нечеткое множество в

∗

...

∗

в виде

(6.65)

где

⎯

- нечеткое множество в

∗

...

∗

, индуцируемое

. Для функции

принадлежности имеем

(6.66)

где

может быть выражено как функция от

,...,u

N-1

путем последовательного

применения уравнения (6.64).

Для многошаговых процессов целесообразно представить решение в виде [54]:

где

- принятая "стратегия" или правило выбора входного воздействия

в зависимости от

состояния системы

Таким образом, задача сводится к нахождению оптимальных стратегий

и соответствующей

последовательности входных воздействий

,...,u

N-1

, максимизирующих в (6.66). Для

ешения задачи применяется метод динамического программирования. Используя (6.64) и

(6.65), имеем

(6.67)

где (6.68)

может рассматриваться как функция принадлежности нечеткой цели в момент

t = N-1

индуцированной заданной целью

в момент

t = N

Повторяя процесс обратных итераций, получаем систему рекуррентных уравнений

(6.69)

которая дает решение задачи. Таким образом, максимизирующее решение получается

последовательной максимизацией величин в (6.69), причем определяется как

функция от .

В качестве простого примера рассмотрим систему с тремя состояниями

и двумя

входными сигналами

. Пусть

N=2

и нечеткая цель в момент времени

t=2

определяется

функцией принадлежности, принимающей значения

Пусть далее, нечеткие ограничения в моменты

t=0

t=1

задаются функциями

Допустим, что таблица изменения состояний, задающая функцию

в (6.64), имеет следующий

вид

Используя (6.69), находим функцию принадлежности нечеткой цели в момент

t=1

Соответствующее максимизирующее решение имеет вид

Аналогично для

t = 0

имеем

и .

Итак, если начальное

состояние в момент времени

t=0

есть

, то максимизирующим

ешением будет

, причем соответствующее значение функции принадлежности

авно 0,8.

6.5. Особенности контроля и управления в условиях

стохастической неопределенности

При составлении проекта редко располагают необходимой для синтеза системы управления

полной априорной информацией об объекте и окружающей его среде. Даже если известны

системы уравнения, описывающие поведение системы, то часто оказывается, что нет данных

о величине отдельных параметров и к тому же нередко имеющиеся модели слишком сложны.

В дальнейшем оказывается, что принятая при проектировании модель существенно

отличается от реального объекта, что значительно уменьшает эффективность разработанной

системы управления. В связи с этим актуальной становится возможность уточнения модели

на основе наблюдений, пол

ченных в

словиях но

мального

фу

нкциони

ования объекта.

Таким образом, задача идентификации формулируется следующим образом: по результатам

наблюдений над входными и выходными переменными системы должна быть построена

оптимальная в некотором смысле модель, т.е. формализованное представление этой системы.

В зависимости от априорной информации об объекте управления различают задачи

идентификации в узком и широком смысле. В последнем случае приходится предварительно

ешать большое число дополнительных проблем. К ним относятся: выбор структуры системы

и задание класса моделей, оценка степени стационарности и линейности объекта, степени и

формы влияния входных воздействий на состояние, выбор информативных переменных и др.

Задача идентификации в узком смысле состоит в оценке параметров и состояния системы по

езультатам наблюдений над входными и выходными переменными, полученными в

условиях функционирования объекта. Для решения отмеченных проблем в современной

теории управления обычно используют модели в пространстве состояний.

Проблеме построения алгоритмов управления объектами с неполной информацией в

настоящее время уделяется большое внимание. Это объясняется прежде всего тем, что при

создании систем управления сложными технологическими процессами обычно не

асполагают достоверными моделями объектов. Ни одна из существующих теорий не может

претендовать на то, что единственно она дает правильное описание работы систем. Скорее

имеется целый спектр теорий, трактующих эти проблемы. При имеющемся сейчас узком

ассмотрении лишь отдельных процессов и только на определенных уровнях описания

получается одностороннее представление о системе, не позволяющее иметь достоверные

оценки обо всех процессах.

Поведение реальной системы характеризуется некоторой неопределенностью, причем при

достаточно большом объеме информации об объекте внешнее возмущение, действующее на

управляемый объект, можно представить как случайный процесс.

Стохастическое оптимальное управление в значительной степени базируется на основных

положениях динамического программирования.

Для линейных систем с квадратичным критерием решение дается так называемой теоремой

азделения, которая позволяет составлять оптимальную стратегию из двух частей:

оптимального фильтра, который вычисляет оценки состояния в виде условного среднего при

заданных наблюдениях выходных сигналов и линейной обратной связи. Оказывается, что

линейная обратная связь может быть найдена путем решения задачи детерминированного

управления. Оценка состояния характеризует выходную переменную фильтра Калмана,

который по существу представляет математическую модель системы, когда управление

осуществляется по наблюдениям. Таким образом, теорема разделения обеспечивает связь

между теориями фильтрации и стохастического оптимального управления.

Описание многомерных динамических объектов.

Под "состоянием" объекта понимают

совокупность величин, полностью определяющих его положение в данный момент и

играющих роль начальных условий для всего будущего движения. Такой путь описания

обладая рядом математических преимуществ, получил значительное распространение в

анализе систем и особенно систем, подверженных случайным воздействиям.

Математические описания динамических объектов при случайных воздействиях внешне

ничем не отличаются от соответствующего описания объектов в детерминированной

постановке. Однако за внешним сходством скрываются существенные особенности,

заключающиеся в том, что в этом случае, как вектор состояния,

так и вектор выходных

переменных объекта представляют собой случайные процессы, порождаемые либо

случайными возмущениями на входе объекта, либо случайными начальными условиями, либо

помехами в каналах изме

ений.

Выбор вектора состояния и вывод уравнения состояния являются начальным этапом

азработки систем управления динамическими объектами, поскольку первичное описание

объектов задается обычно в виде системы дифференциальных уравнений в частных

производных.

Исследование

словий наблюдаемости и идентифицир

емости фильтров Калмана при

моделировании процессов.

Оптимальное управление, оценка и идентификация возможны

только в том случае, когда имеет место управляемость, наблюдаемость и

идентифицируемость. Поведение динамического объекта может описываться уравнением

состояния

k+1

=ФX

+ГQ

(6.70)

при следующей схеме измерений:

=HX

, (6.71)

где

-вектор замеров (пластовых давлении);

H[m:n]

- матрица измерений.

В этом случае возникает вопрос: при каких условиях можно получить необходимую

информацию о состоянии объекта, измеряя его выходные сигналы.

Таким образом, имеем

= HX

; (6.72)

=HX

=HФX

;

…

n-1

=HФ

n-1

или транспонируя, получаем

(6.73)

Так как векторы

известны, существует единственное решение

, когда матрица

N=[H

… (Ф

)

n-1

]

(6.74)

Имеет ранг n. В этом случае пара

(Ф,Н)

называется наблюдаемой. Тогда, если принять

нестационарную систему

(6.75)

квазистационарной на интервале дискретности T, то условия полной наблюдаемости системы

(6.70) можно свести к нахождению ранга матриц

в опорных точках траектории

коэффициентов матриц

, H

, где k

количество опорных точек или интервалов

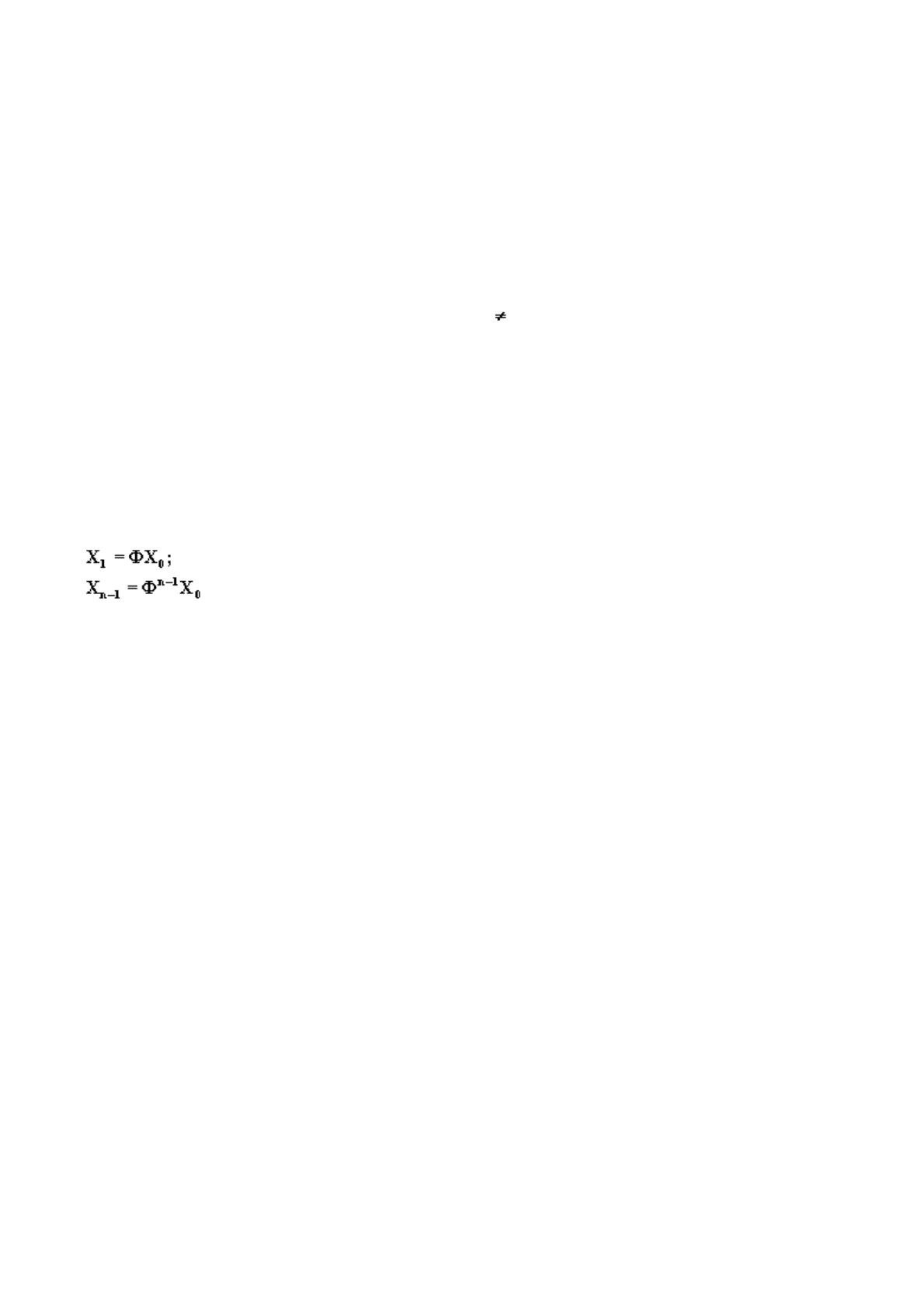
дискретности. Естественно, при высоких размерностях вектора состояния решение этой

задачи требует довольно сложных алгоритмов и значительного объема вычислений. Чтобы

устранить эти затруднения, образуют новые матрицы наблюдаемости

, в виде

, (8.76)

где

, - всегда квадратные матрицы размерностью n,n. Таким образом, оценка

наблюдаемости многомерных нестационарных объектов может быть сведена к простой

процедуре вычисления в опорных точках определителей матриц

. При этом для полной

наблюдаемости объекта необходимо, чтобы

det W

При построении адаптивных систем управления нестационарными объектами учет условий

идентифицируемости, как и условий наблюдаемости, является принципиально необходимым.

В противном случае задача не может быть решена или же будут получены неправильные

езультаты с физической точки зрения. Предполагая, что скорость изменения параметров

нестационарной системы достаточно мала по сравнению со временем переходного процесса в

системе, нестационарную систему можно заменить эквивалентной системой с кусочно-

постоянными параметрами. Тогда условие идентифицируемости можно получить следующим

образом:

(6.77)

или

… X

n-1

]= Ф[X

Ф X

… Ф

n-1

]

. (6.78)

Так как векторы

известны, существует единственное решение для

, когда матрица

V=[X

ФX

… Ф

n-1

]

(6.79)

имеет ранг n.

Синтез алгоритмов оптимальной оценки состояния.

При невозможности прямого

измерения всех компонент вектора состояния, обычный классический подход к оценке

методом наименьших квадратов приводит к использованию непоследовательных схем

оценки, основной недостаток которых состоит в необходимости повторять полный расчет

каждый раз, когда производится дополнительное наблюдение. Рекуррентные алгоритмы дают

возможность уменьшить количество

вычислительных операций и существенно упрощают

программирование задач оценки. Алгоритм оптимальной в среднеквадратическом смысле

оценки состояния динамической системы можно записать в виде

k+1,k+1

k+1,k

k+1

-H

k+1

-H

k+1

k+1,k

;

k+1,k

=Ф

k+1,k

k,k

+Г

k+1,k

;

k+1

k+1,

k+1

)

-1

; (6.80)

k+1,k

=Ф

k+1,k

k,k

k+1,k

;

k+1,k+1

=(I-K

k+1

k+1,k

Формулы (6.80) образуют рекуррентный алгоритм обработки измерений объекта управления.

Новая оценка состояния строится как экстраполированная по уравнениям динамики системы,

старая оценка плюс "взвешенная" разность между измерением выхода и прогнозом этого

измерения на основании прошлых измерений". Для начала рекуррентной процедуры

вычисления необходимы априорные сведения о ковариационных матрицах шумов

e, R

начальном состоянии системы

0,0

Полученный алгоритм оценки состояния совпадает с фильтром Калмана, так как в основе

алгоритмов лежит один и тот же критерий оптимальности и приняты те же самые

ограничения.

Однако в отличие от существующих алгоритмов здесь рассматривается управляемое

движение нестационарных объектов, и при этом учитываются ошибки измерений и

нестационарность внешних возмущений.

Использование фильтров Калмана для оценки вектора

k,k

предполагает наличие большой

оперативной памяти ЭВМ и связано с методами декомпозиции исследуемого процесса.

Поэтому для практических целей удобнее применять методы стохастической аппроксимации.

Обозначим скалярный показатель качества идентификации определяемый в виде

(6.81)

Оценка вектора состояния получается из алгоритма стохастической аппроксимации

следующим образом:

(6.82)

Для обеспечения сходимости последовательность

. должна удовлетворять условиям

Дворецкого.

6.6. Контроль и управление динамическими системами в

нечетких условиях

Применение стохастических методов для контроля и управления процессом в некоторых

ситуациях оказывается затруднительным ввиду отсутствия вероятностных распределений

параметров. Сложность получения численных результатов при работе со случайными

величинами также снижает практическую ценность стохастических алгоритмов.

В случае неполной информации о сложном процессе удобнее представлять неточно заданные

параметры в виде нечетких величин и при работе с

ними пользоваться предложенными в

данной работе методами.

Коэффициенты целого ряда моделей фактически зависят от многих факторов реального

оцесса, не

чтенных в модели. П

и описании п

оцессов дв

хме

ными моделями мы