Alfred DeMaris - Regression with Social Data, Modeling Continuous and Limited Response Variables

Подождите немного. Документ загружается.

TRUNCATION AND CENSORING DEFINED 315

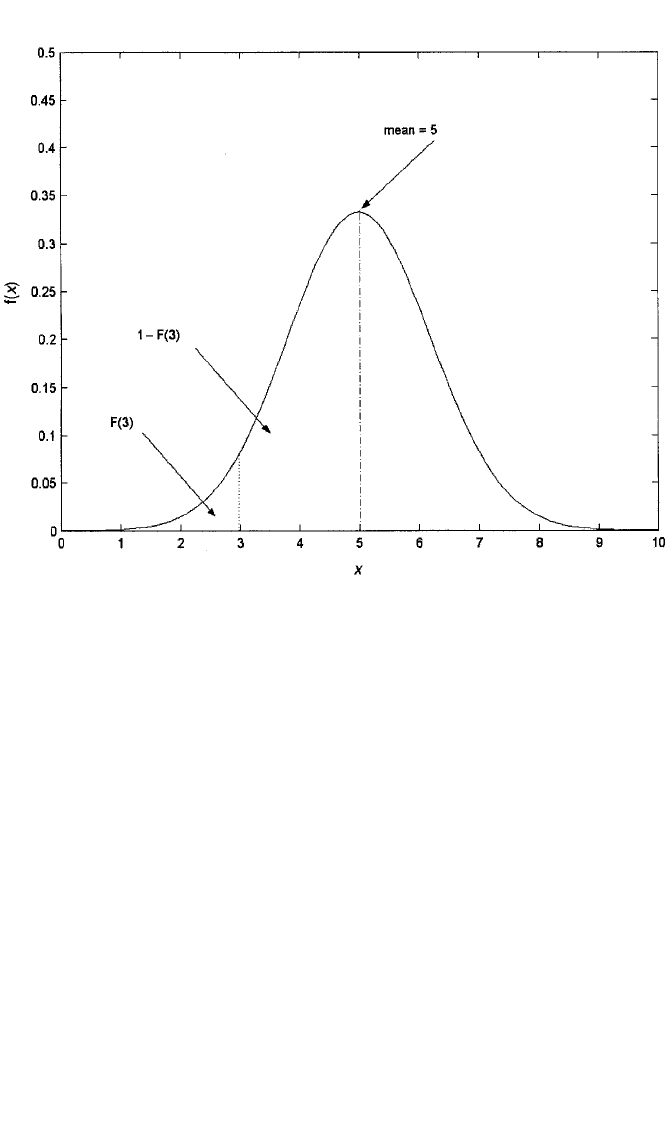
a standard deviation of 1.2. Figure 9.1 shows the density of X. Notice the dotted line

at the point x ⫽ 3. Recall that f(x), the density of x, is the point on the curve corre-

sponding to x. For example, f(3) is the point on the curve corresponding to 3. F(x),

on the other hand, is the area under the curve to the left of x. Hence, F(3) is the area

to the left of 3 in Figure 9.1, while 1 ⫺ F(3) is the area to the right of 3. If the pop-

ulation of X values were the target population, a random sample taken from this dis-

tribution would be representative of that target population.

However, suppose that we were to draw a sample under the condition that X be

greater than 3. It is then not possible to observe values of X less than or equal to 3 in

the sample, and we say that the density (or distribution) from which we are sampling

is truncated at 3. That is, the sample is a random sample in the usual sense, but the

“population” from which it is being drawn is now truncated at 3. The population, or

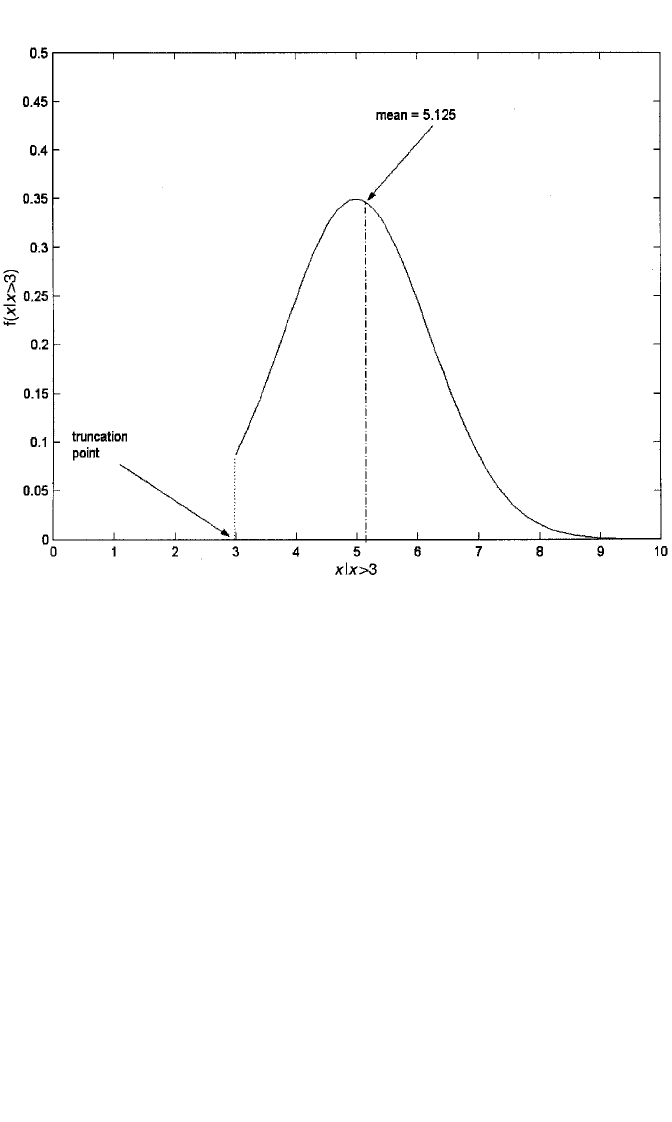
density, that applies in this case is depicted in Figure 9.2. The sample is no longer rep-

resentative of the target population shown in Figure 9.1; rather, it is representative of

the population in Figure 9.2. Moreover, the density in Figure 9.2 is not simply the part

of Figure 9.1 that is to the right of 3. Rather, in order for the resulting function,

denoted f(x 冟 x ⬎ 3), to remain a density, it must be rescaled so that the total area under

the curve is, again, 1. This is done by dividing the original density by 1 ⫺ F(3), the

area to the right of 3. That is, in general, if X is normal with density function f(x),

Figure 9.1 Normal density with mean ⫽ 5 and standard deviation ⫽ 1.2.

c09.qxd 8/27/2004 2:55 PM Page 315

316 TRUNCATED AND CENSORED REGRESSION MODELS

mean µ, standard deviation σ, and truncation from below at the point c, then

f(x 冟 x ⬎ c) is

f(x 冟x ⬎ c) ⫽

ᎏ

1 ⫺

f(x

)

(c)

ᎏ

. (9.1)

In the case of truncation from above, we obtain f(x 冟 x ⬍ c) by dividing f(x) by F(c)

(see Greene, 2003; Wooldridge, 2000).

What does truncation do to the mean and variance of the new (i.e., truncated) ran-

dom variable? From Greene (2003, p. 759) we have the following moments of the

truncated normal distribution. If X is normal with mean µ and standard deviation σ,

and X is truncated from below at c, then

E(X 冟truncation) ⫽ µ ⫹ σλ (α), (9.2)

V(X 冟truncation) ⫽ σ

[1 ⫺ δ(α)], (9.3)

where

α ⫽

ᎏ

c ⫺

ᎏ

, (9.4)

Figure 9.2 Truncated normal density with mean ⫽ 5.125 and standard deviation ⫽ 1.083.

c09.qxd 8/27/2004 2:55 PM Page 316

TRUNCATION AND CENSORING DEFINED 317

λ(α) ⫽

ᎏ

1 ⫺

φ(

(

)

α)

ᎏ

, (9.5)

δ(α) ⫽ λ(α)[λ(α) ⫺ α], (9.6)

and where φ(α) and Φ(α) are the standard normal density and distribution functions,

respectively. Moreover, note that 0 ⬍ δ(α) ⬍ 1 for all values of α. Notice that α is

just the z-score for c, that is, it measures the number of standard deviations that c is

away from µ. The term λ(α) is called the inverse Mills ratio (IMR), or hazard func-

tion, for the standard normal distribution (Greene, 2003). As it plays an integral part

in all of the models in this chapter, it is worth examining in closer detail.

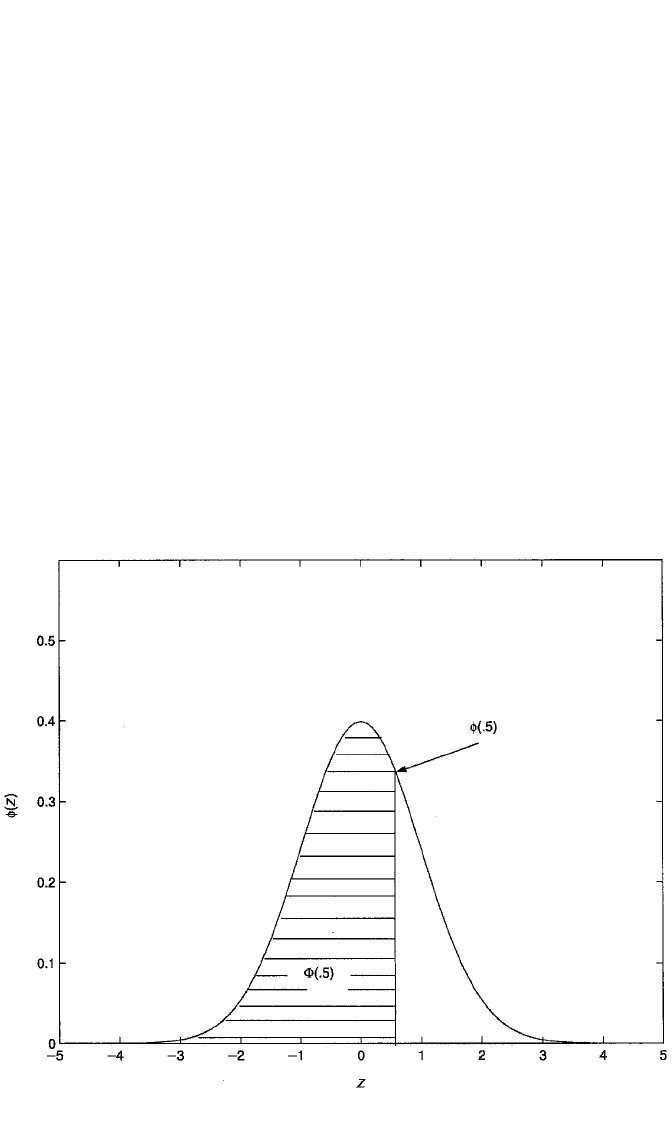
Figure 9.3 depicts the major components of the IMR. Shown is the standard nor-

mal distribution with mean 0 and standard deviation 1. Letting α ⫽ .5 in this case,

we see that φ(.5) is the density associated with .5 and is equal to

φ(.5) ⫽

ᎏ

兹2

苶

)

苶

ᎏ

exp

冤

⫺

ᎏ

(.5

)

冥

⫽ .352

and Φ(.5) is the shaded area to the left of .5 under the curve, which is equal to .691

(using a table of areas under the standard normal curve). One minus Φ(.5), therefore,

Figure 9.3 Components of the inverse mills ratio (hazard rate) for the standard normal density.

c09.qxd 8/27/2004 2:55 PM Page 317

is the unshaded area that lies to the right of .5 and is equal to .309. The IMR for .5,

denoted λ(.5), is the ratio φ(.5)/[1 ⫺ Φ(.5)], or .352/.309 ⫽ 1.139. In general, as z

becomes increasingly negative, φ(z) approaches zero while 1 ⫺ Φ(z) approaches 1,

so λ(z) approaches zero. As z becomes increasingly positive, on the other hand, both

φ(z) and 1 ⫺ Φ(z) approach zero. It turns out, however, that 1 ⫺ Φ(z) approaches zero

more rapidly; hence λ(z) actually increases without bound. In other words,

lim

z→⬁

λ(z) ⫽⬁. So the theoretical range of λ(z) is (0,⬁); however, given that virtu-

ally all of a standard normal variable lies within 4 standard deviations of its mean,

the practical range of the IMR is approximately (0, 4.2). (I postpone further inter-

pretation of the IMR until we get to sample-selection models.)

Returning to the distribution in Figure 9.2, α is (3 ⫺ 5)/1.2 ⫽⫺1.667, φ(⫺1.667)

is .0994, and 1 ⫺ Φ(⫺1.667) is .9522. Hence, λ(α) ⫽ .0994/.9522 ⫽ .1044, and the

mean of the distribution is therefore 5 ⫹ 1.2(.1044) ⫽ 5.125. Now δ(α) ⫽ .1044

[.1044 ⫺ (⫺1.667)] ⫽ .185. So the variance of the distribution is (1.2

)(1 ⫺ .185) ⫽

1.083. As is evident from the formulas for the truncated mean and variance, and as

shown in this example, truncation from below results in an increase in the mean but

a reduction in the variance. [Truncation from above results in a reduction in both the

mean and the variance; see Greene (2003) for details.]

Censoring

Suppose that we sample from the untruncated distribution of X shown in Figure 9.1 but

that for all X below the value of 3, we simply record X as being equal to 3. In this case

the sample is drawn from the full target population, but it is not fully representative of

that population with respect to the values of X, since a portion of the values have been

“censored” at 3. That is, for those observations, all we know is that X is less than 3. We

say that the sample is censored at 3. Censoring, unlike truncation, does not represent a

limitation in the population from which the data were drawn. Rather, it represents a

limitation in the measurement of the variable of interest. If the data were not censored,

they would be representative of the target population with respect to X (Greene, 2003).

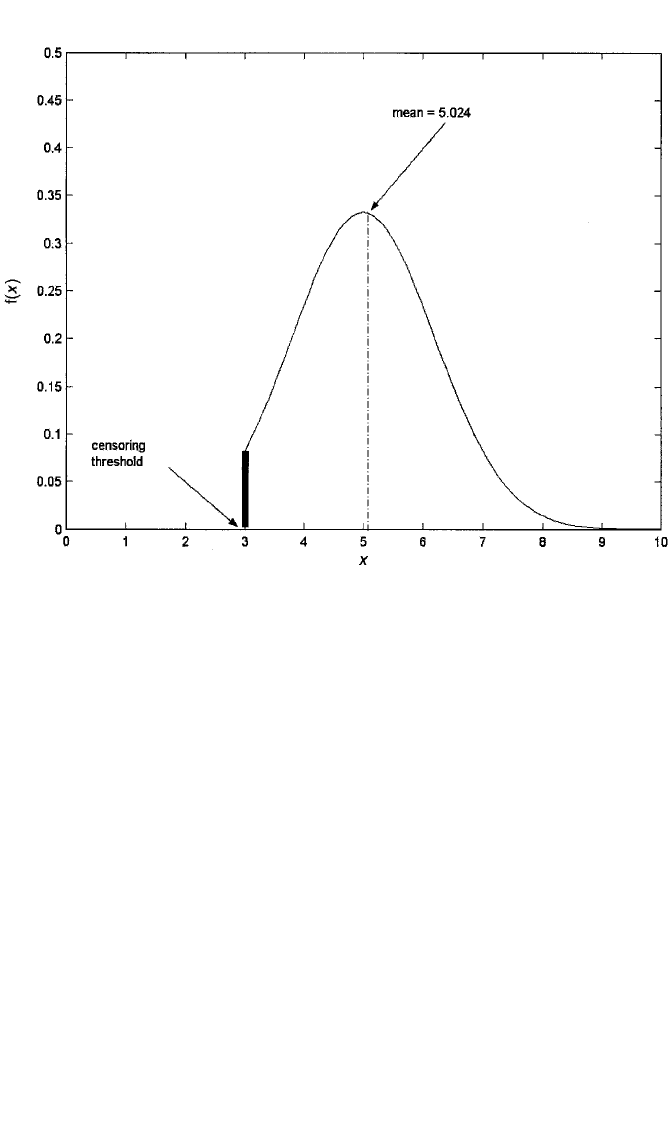
The density that applies to censored data is actually a mixture of discrete and con-

tinuous densities and for the current example is shown in Figure 9.4. For values of X

above 3, the density is just the f(x) shown in Figure 9.1. However, for X ⫽ 3, the den-

sity is the probability that X is less than 3. (Recall from Chapter 1 that for a continu-

ous X,P[X ⬍ 3] and P[X ⱕ 3] are the same.) That is, we assign the area F(3) to be the

density corresponding to the value 3. This is depicted as a solid bar above the value

of 3 in Figure 9.4. Again, I draw on a theorem presented in Greene (2003, p. 763) to

calculate the moments of the censored normal variable. If X is normal with mean µ

and standard deviation σ, and X is censored from below at the threshold c, then

E(X 冟censoring) ⫽ Φ(α)c ⫹ [1 ⫺ Φ(α)] [µ ⫹ σλ(α)], (9.7)

V(X 冟censoring) ⫽ σ

[1 ⫺ Φ(α)] [(1 ⫺ δ(α)) ⫹ [α ⫺ λ(α)]

Φ(α)], (9.8)

where α, λ(α), and δ(α) are deﬁned as in expressions (9.4) to (9.6). For the current

example, then, E(X 冟 censoring at 3) ⫽ (.0478)(3) ⫹ .9522[5 ⫹ 1.2(.1044)] ⫽ 5.024; and

318 TRUNCATED AND CENSORED REGRESSION MODELS

c09.qxd 8/27/2004 2:55 PM Page 318

TRUNCATION AND CENSORING DEFINED 319

V(X 冟censoring at 3) ⫽ 1.2

(.9522)[(1 ⫺ .185) ⫹ (⫺1.667 ⫺ .1044)

(.0478)] ⫽ 1.323,

in which case σ⫽ 1.15.

Both truncation and censoring involve limits on the response variable that are

based on the values of the response variable itself. Another form of truncation, known

as incidental truncation, involves limits on the response variable that are imposed by

the values of another variable. This other variable can be denoted Z*. When Z* is

greater than some threshold, c, values of X are observed. Otherwise, they are missing.

This is the conceptual underpinning for statistical solutions to the problem of sample-

selection bias, that is, the bias in OLS estimates of a population regression in which

there is self-selection into the sample (Heckman, 1979). I shall postpone discussion

of incidentally truncated data until I have introduced the simulation data below.

Simulation

For the purposes of introducing each of the models in this chapter, I created some

simple data that follow the assumptions required for each model. With this approach,

I intend to use ideal conditions to illustrate the advantages of truncated, censored,

and sample-selected regression models over linear regression estimated via OLS, so

that the reader can clearly see how each model is supposed to work. (Subsequently,

of course, we will “dirty things up” with real data and consider how these models

Figure 9.4 Density of the censored normal variable with mean ⫽ 5.024 and standard deviation ⫽ 1.15.

c09.qxd 8/27/2004 2:55 PM Page 319

actually work in practice.) Hence I constructed a data set consisting of 1000 obser-

vations with the following variables: a variable ε that is normally distributed with

mean 0 and variance 4, a variable u that is normally distributed with mean 0 and vari-

ance 1, a variable X that is normally distributed with mean 3 and variance 1.75 but

is assumed to be ﬁxed over repeated sampling, a variable W equal to 1 ⫹ .75X ⫹ u,

and a variable Y equal to ⫺2 ⫹ 1.5X ⫹ ε. Moreover, ε and u were created so that their

joint distribution is bivariate normal, and their correlation, ρ, is .707. Otherwise, ε

and u are both uncorrelated with X.

What we essentially have, then, is a random sample of n ⫽ 1000 observations on

two variables of primary interest: X and Y. Moreover, Y follows a linear regression

on X with an intercept of ⫺2 and a slope of 1.5. The conditional error, ε, is normally

distributed with a mean of zero and a variance of 4. The unconditional mean of Y

is E(Y) ⫽ E(⫺2 ⫹ 1.5X ⫹ ε) ⫽⫺2 ⫹ 1.5E(X) ⫹ E(ε) ⫽⫺2 ⫹ 1.5(3) ⫹ 0 ⫽ 2.5. The

unconditional variance of Y can be recovered by noting that if Y ⫽⫺2 ⫹ 1.5X ⫹ ε,

then V(Y ) ⫽ V(⫺2 ⫹ 1.5X ⫹ ε) ⫽ V(⫺2 ⫹ 1.5X) ⫹ V(ε) ⫽ (1.5)

V(X) ⫹ V(ε) ⫽ 2.25

(1.75) ⫹ 4 ⫽ 7.9375. Moreover, the contribution due to the structural part of the model,

the linear predictor, is 2.25(1.75) ⫽ 3.9375, which represents 49.6% of the total vari-

ance of Y. Hence, P

, the population R

for the regression, is .496. The regression

model for Y is one of the equations we will be trying to estimate in what follows.

To create truncated and censored data, I proceeded as follows. To truncate or cen-

sor 40% of the observations on Y, I created a variable Y* ⫽ Y ⫺ c, where c is the value

(1.859) representing the 40th percentile of the sample distribution on Y. This simply

sets the truncation point and censoring thresholds at zero rather than at c. Then I cre-

ated a truncated version of Y, Y

, by setting Y

to missing when Y* ⱕ 0, and setting

⫽ Y* otherwise. To create a censored version of Y, Y

, I set Y

to 0 whenever Y* ⱕ 0,

and I set Y

⫽ Y* otherwise. Notice that this changes the underlying regression model

slightly. By subtracting 1.859 from both sides of the equation for Y, we see that Y* ⫽

⫺3.859 ⫹ 1.5X ⫹ ε. This is the equation we are trying to estimate in the truncated and

censored regression examples. In the sample, we have 601 observations on Y

, with

the other 399 observations missing on Y

. We have 1000 observations on Y

, but for

399 of them the value of Y

is zero. For the other 601 observations, Y

takes on posi-

tive values.

Incidentally truncated data were created in a somewhat diﬀerent manner. First, I

chose a new value of c (3.634) that constituted the 60th percentile for the sample dis-

tribution of W. I then constructed a variable Z* equal to W ⫺ 3.634. In this case, Z*

is less than or equal to zero for 60% of the cases. I then created a dummy variable,

Z, equal to 0 whenever Z* ⱕ 0, and equal to 1 otherwise. I then set Y to missing if

Z ⫽ 0; otherwise, Y is left as is. In the current example, then, only 400 cases have

valid scores on Y. The variable Y here is said to be incidentally truncated. I refer to

Z* as the selection propensity. When Z* is above zero, the case is selected into the

current sample (of responses) and we observe Y. Otherwise, we do not observe Y for

that case, although we do observe X. This is the model employed to understand and

correct for self-selection bias (more on this below). Recall that Y has a mean of 2.5

and a variance of 7.9375. What does incidental truncation do to the population mean

and variance of the truncated response? As before, I draw on a result presented in

320 TRUNCATED AND CENSORED REGRESSION MODELS

c09.qxd 8/27/2004 2:55 PM Page 320

Greene (2003, p. 781) for the moments of the incidentally truncated bivariate normal

distribution: If y and z have a bivariate normal distribution with means µ

and µ

standard deviations σ

and σ

, and correlation ρ, then

E(y 冟z ⬎ a) ⫽ µ

⫹ ρσ

λ(α

), (9.9)

V(y 冟z ⬎ a) ⫽ σ

[1 ⫺ ρ

δ(α

)], (9.10)

where

⫽

ᎏ

a ⫺

ᎏ

, (9.11)

λ(α

) ⫽

ᎏ

1 ⫺

φ(

(

)

ᎏ

, (9.12)

δ(α

) ⫽ λ(α

)[λ(α

) ⫺ α

]. (9.13)

In the current example, recall that ε and u are distributed as bivariate normal with

a correlation of .707. Also, since Z* ⫽ W ⫺ 3.634 ⫽ 1 ⫹ .75X ⫹ u ⫺ 3.634, the equa-

tion for Z* is ⫺2.634 ⫹ .75X ⫹ u. And, of course, the equation for Y is ⫺2 ⫹ 1.5X ⫹ ε.

By theorem, a linear function of a normal random variable is also normally distrib-

uted (Hoel et al., 1971), so Z* and Y, both being linear functions of normally distrib-

uted errors, are also normally distributed, with a correlation (ρ) of .852 (found using

covariance algebra). This also implies that Z* and Y are bivariate normally distributed

(Hoel et al., 1971). We can therefore apply the theorem above to ﬁnd the mean and

variance of Y, where Z* ⫽ “z” above and 0 ⫽ “a.” Using principles of expectation,

along with covariance algebra and some simple arithmetic, we also have α

⫽ .273,

⫽ 2.5, σ

⫽ 2.817, λ(α

) ⫽ .98, and δ(α

) ⫽ .692. Thus,

E(Y 冟Z*⬎ 0) ⫽ 2.5 ⫹ .852(2.817)(.98) ⫽ 4.852,

V(Y 冟Z*⬎ 0) ⫽ 2.817

[1 ⫺ .852

(.692)] ⫽ 3.949.

Once again, we see that truncation has increased the mean, but reduced the variance,

of Y. At this point, we have the tools needed to understand the regression models pre-

sented in this chapter.

TRUNCATED REGRESSION MODEL

The truncated regression model is based on the following idea. First, we assume that

there is an “underlying” regression model for Y in the target population that follows

the classic linear regression assumptions. That is, we assume that

⫽ x

⬘

ββ

⫹ ε

, (9.14)

TRUNCATED REGRESSION MODEL 321

c09.qxd 8/27/2004 2:55 PM Page 321

where as in previous chapters, x

⬘

ββ

represents β

⫹ β

⫹⭈⭈⭈⫹β

, and

is normally distributed with mean zero and variance σ

. However, the sample is

restricted so that we only select cases in which Y is greater than c, where c is some

constant. A substantive example would be a study of factors aﬀecting college GPA

using a random sample of sociology majors at a particular university. In that one

must have a minimum GPA of 3.0 to have a declared major in sociology at this insti-

tution, the sample is necessarily restricted to those with GPAs of 3.0 or higher and

is therefore not representative of college students in general.

Now, suppose that one were to use the truncated response to estimate the regression

model for Y using OLS. What are we actually estimating? First, understand that using

a sample drawn from a truncated population implies that what is being estimated is the

regression function in the truncated population, not the regression function in the gen-

eral population. Then, note that Y

is greater than c only if x

⬘

ββ

⫹ ε

⬎ c, or only if

⬎ c ⫺ x

⬘

ββ

. Therefore, the conditional mean of Y in the truncated population is

E(Y

冟Y

⬎ c, x

) ⫽ E(x

⬘

ββ

⫹ ε

冟ε

⬎ c ⫺ x

⬘

ββ

)

⫽ x

⬘

ββ

⫹ E(ε

冟ε

⬎ c ⫺ x

⬘

ββ

To derive E(ε

冟ε

⬎ c ⫺ x

⬘

ββ

), we apply equation (9.2), with c equal, in this case, to

c ⫺ x

⬘

ββ

,and µ equal to the mean of ε

, which is zero. By equation (9.2) we have that

E(ε

冟ε

⬎ c ⫺ x

⬘

ββ

) ⫽ 0 ⫹ σλ(α

) ⫽ σλ (α

), (9.15)

where

⫽

ᎏ

c ⫺ x

⬘

ββ

⫺ 0

ᎏ

⫽

ᎏ

c ⫺

⬘

ββ

ᎏ

and

λ(α

) ⫽

ᎏ

1 ⫺

φ(

(

)

ᎏ

Therefore, the conditional mean of Y is

E(Y

冟Y

⬎ c, x

) ⫽ x

⬘

ββ

⫹ σλ (α

). (9.16)

To answer the previous question, then, equation (9.16) is what we are inadvertently

trying to estimate with OLS. But using OLS to estimate this conditional mean will

result in biased and inconsistent estimators of

ββ

, due to the term λ(α

), the IMR, in

the true model for the conditional mean. In that we have no sample measure of the

IMR, using OLS essentially results in omitted-variable bias.

Estimation

In both the censored and sample-selected regression models discussed below, we

have x

for all observations, so it is possible to estimate λ(α

) consistently using OLS

322 TRUNCATED AND CENSORED REGRESSION MODELS

c09.qxd 8/27/2004 2:55 PM Page 322

TRUNCATED REGRESSION MODEL 323

and then to include it in the model as an extra term (see below). However, truncation

results in the exclusion of x

as well as Y

for cases in the sample. Therefore, this two-

step approach is not possible here. Instead, we resort to estimation via maximum

likelihood. Based on the expression in equation (9.1), the likelihood function for the

truncated regression model (Breen, 1996) is

ββ

,σ 冟 y

) ⫽

兿

i⫽1

Maximizing this function with respect to

ββ

and σ gives us the MLEs. Unlike OLS

estimates, the resulting MLEs are consistent, asymptotically eﬃcient, and asymptot-

ically normally distributed.

Simulated Data Example

Recall the simulation of truncated data discussed above. The underlying regression

model is Y*⫽⫺3.859 ⫹ 1.5X ⫹ ε. Table 9.1 presents the results of estimating this

model with OLS using both the full (n ⫽ 1000) and truncated (n ⫽ 601) samples.

With the full sample, OLS estimates should demonstrate the usual properties of

being unbiased and eﬃcient. As is evident from the “OLS: full sample” column,

these parameter estimates are quite close to their true values. In particular, the slope

is estimated as 1.459 compared to its true value of 1.5, and σ is estimated as 1.996

whereas its true value is 2. The truncated data, on the other hand, result in OLS esti-

mates that are quite far from their true values. In fact, all estimates are too small in

magnitude, a general result of using OLS with a truncated response. For example,

the slope is estimated as .847 and σ is estimated as 1.551. The next column, headed

“MLE: truncated sample,” gives the maximum likelihood estimates for the truncated

regression model. (LIMDEP was used to estimate truncated regression models for

this chapter.) Notice again that these are quite close to the true values: the slope is

estimated as 1.438 and σ is estimated as 2.034.

(1/σ) φ[(y

⫺ x

⬘

ββ

)/σ]

ᎏᎏᎏᎏ

1 ⫺ Φ(α

)

Table 9.1 Regression with Simulated Data, Showing Eﬀects of Truncation and

Censoring on Parameter Estimates

OLS: OLS: MLE: OLS:

True Full Truncated Truncated Censored Tobit

Regressor Parameters Values Sample

Sample

Model

Intercept β

⫺3.859 ⫺3.686 ⫺.556 ⫺3.631 ⫺1.154 ⫺3.717

X β

1.500 1.459 .847 1.438 .881 1.465

σ 2.000 1.996 1.551 2.034 1.464 2.018

.496 .482 .270 .386 .478

n ⫽ 1000.

n ⫽ 601.

c09.qxd 8/27/2004 2:55 PM Page 323

324 TRUNCATED AND CENSORED REGRESSION MODELS

Application: Scores on the First Exam

To show an application of truncated regression, I employ an artiﬁcial data scenario

for heuristic purposes. Using the students dataset, I once again (as in Chapter 3)

examine the regression of ﬁrst exam score, but this time I only sample students with

scores of 70 or better. There are 149 such cases out of the 214 students who took that

exam. Normally, there would be no reason to limit the response variable in this man-

ner unless, say, we only had information on explanatory variables for students with

grades of at least 70, or a similar constraint. At any rate, Table 9.2 shows the results

of regressing ﬁrst exam score on college GPA, math diagnostic score, and attitude

toward statistics, using both OLS and MLE on the truncated sample. Once again,

with the exception of the intercept, all parameter estimates from OLS are smaller in

magnitude than those from the truncated regression model. Interpretation of the

coeﬃcients in either model pertains to the entire population of students taking intro-

ductory statistics at BGSU, not just to those with ﬁrst exam scores above 70. Thus,

the coeﬃcient for math diagnostic score in the truncated regression model suggests

that each unit higher a student scores on the math diagnostic is associated with being

1.164 points higher on the ﬁrst exam on average, net of the other regressors. The

other coeﬃcients are interpreted in a similar fashion.

CENSORED REGRESSION MODEL

To motivate the censored regression model we once again begin with the presump-

tion of an underlying regression model that pertains to the target population. This

time we denote the underlying response as Y

. The model for Y

in the target popu-

lation is

⫽ x

⬘

ββ

+ε

, (9.17)

where, as before, ε

is assumed to be normally distributed with mean 0 and variance

. However, in our sample, the response is censored at a lower threshold of c,

Table 9.2 Unstandardized OLS and ML Estimates for the

Truncated Regression Model of Exam 1 Scores

OLS ML

Regressor Estimates Estimates

Intercept 23.728* 4.348

College GPA 7.484*** 9.437***

Math diagnostic score .889*** 1.164***

Attitude toward statistics .175 .224

7.833 8.645

.262

Note: n ⫽ 149.

* p ⬍ .05. ** p ⬍ .01. *** p ⬍ .001.

c09.qxd 8/27/2004 2:55 PM Page 324