Алексеев В.В. Физическое и математическое моделирование экосистем

Подождите немного. Документ загружается.

Тогда G(p) преобразуется к виду

к* (

\ 8

УР) — 1 — 6*ехр(р + (х)а '

характеристическое уравнение приобретает форму

1-6*ехр[

—

а]

(6.46)

Произведение Sg определяет взаимное влияние консумента и расте-

ний;

Sg= (влияние консумента на ресурс) X (влияние ресурса на

рождаемость консумента). Урав-

нение

(6.46)

имеет бесконечное Im.p

число корней (собственных зна-

чений)

для каждого значения Sg.

При

изменении Sg от нуля до

бесконечности,

каждый корень

описывает траекторию на комп-

лексной

плоскости. Локализация

Рис.

6.11. Общее расположение

корней

характеристического урав-

нения

(6.46) на комплексной пло-

скости.

корней

может служить хорошей иллюстрацией динамики линеари-

зованной

системы при разных режимах внешних условий.

Для случая Bg = О, уравнение

(6.46)

редуцируется к виду

) = 0. (6.47)

Уравнение

(6.47)

имеет следующие корни.

(6.48)

Уравнение

(6.48)

имеет один действительный корень р —lnft*/a —

—

ц = р и комплексные корни, определяемые из условия р = р ±

/со, откуда со = 2яп/а (п = 1, 2...).

Общее расположение корней показано на рис. 6.11 для случая

b(a) =

b*6{a

— а). Ветви начинаются при Bg — 0{l) и проведены

до Sg = + оо (2). Корни уравнения

(6.46)

при каждом фиксиро-

ванном

значении Sg находятся на ветвях, как отмечено, например,

точками Pi (i= I, 2, ...). Зная распределение корней для уравне-

ния

(6.46), можно получить частотные отклики на периодическое

воздействие u(t) для ресурса #(ко)/е7(ио) и общей плотности по-

221

пуляции Y(i(u)/U(m). Поскольку первая пара комплексно сопря-

женных корней лежит очень близко к реальной оси, результирую-

щая

резонансная частота может быть бесконечно малой. Из

рис.

6.11 видно, что

существует

область значений параметров,,

которой линеаризованная модель переходит от устойчивости

неустойчивости, т. е. при изменении параметра взаимодействия

Eg в определенной области, первая пара собственных значений

пересекает мнимую ось. В этой точке в нелинейной системе наблю-

даются колебания с малой амплитудой, которая в дальнейшем

растет при увеличении Eg.

Если

окно

репродуктивное™

у консумента имеет конечную

ширину

7. то уравнение

(6.46)

должно быть заменено на уравне-

ние

(6.44), и характеристическое уравнение приобретает вид

Корни

р = — А; р = — ц остаются на месте, как и в предыдущем

случае, исследование комплексных корней оказывается более

сложным, однако качественное поведение системы остается

прежним.

6.5.

Трофические системы

возрастным

распределением

Объединяя несколько популяций с возрастным распределением,,

можно сформировать систему с трофическими взаимодействиями.

Так,

простейшая система «хищник—жертва» (рис. 6.12) может

Хищник

Жертва

Рис. 6.12.

Система

«хищник—жертва»

при на-

личии

возрастной

структуры

популяций.

быть получена объединением

двух

уравнений типа (6.3), при этом

уравнении для жертвы коэффициент смертности заменяется на

фактор

смертности, зависящий от общей численности

другого

222

вида [117, 119, 272]:

«р + Ур

p(0,

t)= \

(a',

H{t-x))p(a', t)da',

(6-49)

A(0,

t)= j

(a', t)h(a

, t)da',

H(t)=\h(a,

t)da, P(t)=\p(a, t)da,

где

h(a,

t)—плотность возрастного распределения популяции

жертвы; р(а, t)—плотность хищника.

В простейшем случае, когда рождаемость как

хищника, так

жертвы приходится на строго определенный возраст

Ь{а

—

(6.50)

b(a

— a

анализ,

аналогичный проведенному

предыдущем параграфе, дает

для отклонения общей численности хищника

частотном виде вы-

ражение

U tM')

jjgr(«). (6-51)

s +

Цр

1— exp (— a

где Up(s)—вклад окружающей среды

рождаемость хищника.

Для популяции жертвы имеем

(s)=

}. -. \ г

(s)

4*2- Y

(s). (6.52)

M-A 1— exp

(—a^s)

' n^s

Разрешая

алгебраические уравнения (6.50)

(6.51)

относительно

(s)

Vft(s),

получим

I s +

jip

— exp (—sap)

fiftS

s +

t*p 1 — exp

(—sa

)

|ЛрА

1 1

ЦЙ

I— exp

(—

I—

exp(—sa

)

где

(6.53)

223

Из

(6.53)

нетрудно видеть, что кроме резонансных членов

(1—ехр(—sap)) и (1 — ехр(—sa

)), которые наблюдались в изо-

лированных популяциях, общий отклик системы «хищник-жертва»

характеризуется гармонической составляющей вида (s

+ Q

) с ча-

стотой й.

В динамике каждой популяции появляются, как минимум, две

синусоиды, приводящие к новому явлению — гармоническим «бие-

ниям» с частотой, пропорциональной разности

между

частотой

внешнего воздействия и резонансными частотами. Период биений

для частот fii и Q

равен

2n/(Qi — Q

). Таким обра-

зом,

явление «биений» ока-

зывается новым динамиче-

ским

свойством, присущим

связанным

системам.

Система

«паразит—хо-

зяин».

Практические задачи

борьбы с вредными насеко-

мыми

обусловили повышен-

ное

внимание к эксперимен-

тальному и теоретическому

изучению динамики попу-

ляционных

систем «пара-

зит—хозяин» (насекомое и

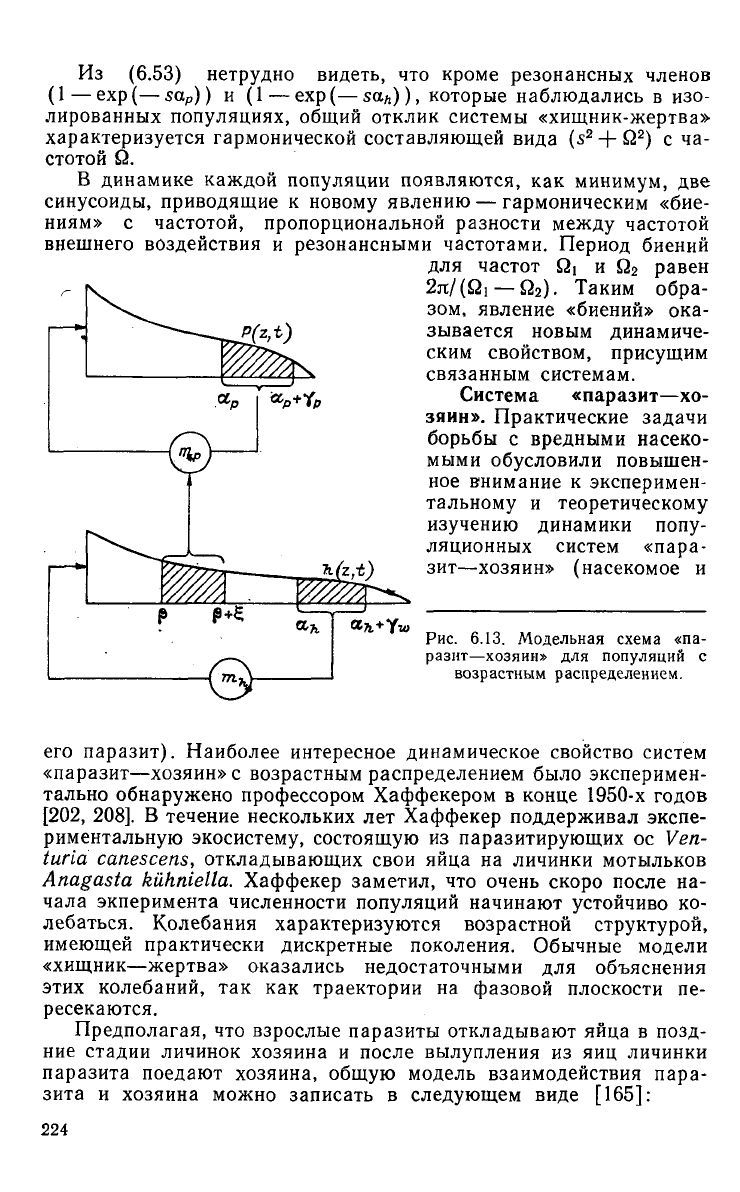
Рис.

6.13. Модельная схема «па-

разит—хозяин»

для популяций с

возрастным

распределением.

его паразит). Наиболее интересное динамическое свойство систем

«паразит—хозяин» с возрастным распределением было эксперимен-

тально обнаружено профессором Хаффекером в конце

1950-х

годов

[202, 208]. В течение нескольких лет Хаффекер поддерживал экспе-

риментальную экосистему, состоящую из паразитирующих ос Ven-

turia

canescens,

откладывающих свои яйца на личинки мотыльков

Anagasta

kiihniella.

Хаффекер заметил, что очень скоро после на-

чала экперимента численности популяций начинают устойчиво ко-

лебаться. Колебания характеризуются возрастной структурой,

имеющей практически дискретные поколения. Обычные модели

«хищник—жертва» оказались недостаточными для объяснения

этих колебаний, так как траектории на фазовой плоскости пе-

ресекаются.

Предполагая, что взрослые паразиты откладывают яйца в позд-

ние

стадии личинок хозяина и после вылупления из яиц личинки

паразита поедают хозяина, общую модель взаимодействия пара-

зита и хозяина можно записать в следующем виде [165]:

224

1) для паразита

(6.54)

р{0, /) = ] т

\а, t, H

)p(a, t)da,

2) для хозяина

dh , dh

—йл^а, *, Я, Я

, Ро)Л,

(0, t)= \ m

(a, t, H

{t—x))hda,

(6.55)

+ 6

+ Vp

p(a,t)da,P(t)

где p(a, t); h(a, t) — плотности популяций паразита и хозяина;

P(t),

H(t) — общие количества особей паразитов и хозяев; #о(О —

число личинок хозяина, подверженных возможности заражения;

Po(t)— число взрослых особей паразита.

Модельная схема системы «паразит—хозяин» представлена на

рис.

6.13.

Центральное биологическое свойство модели — специфика взаи-

модействия

двух

популяций. Простейший вид взаимодействия мо-

жет быть получен из предположения о случайном поиске каждым

паразитом личинок хозяина, считая площадь «обследования» S

для одного паразита либо постоянной, либо зависящей от возра-

ста встречающихся личинок хозяина

(a).

Если личинки хозяина

распределены по плоскости равномерно, то вероятность поражения

паразитом является пуассоновским процессом. Взаимодействие

между

паразитом и хозяином принимает вид

[

Число

зараженных личинок ]

\--=Ыг{а)[\

— ехр(—S

(a)P

)].

хозяина возраста а \

l v v v

(6.56)

Зараженный

хозяин считается мертвым и заменяется яйцами в по-

пуляции

паразита. Смертность хозяина имеет также некоторую

зависимость от плотности. Плодовитость хозяина включает запа-

здывающий эффект, который определяется его питанием в про-

шлом.

Заказ

№ 57 225

Теоретический анализ показывает, что в системе «паразит—

хозяин», так же, как и в других системах с возраст-специфиче-

скими

взаимодействиями, можно наблюдать резонансные явления.

Рассмотрим линеаризованный вариант уравнений (6.55). Пусть

(а, s) и Xh(a, s)—преобразования Лапласа для плотностей па-

разита и хозяина р(а, t), h(a, t). Определим преобразования для

взаимодействующих популяционных сегментов как

+ б

(s)= \ X

da,

H(s)= \ X

da,

«p + Vp

P(s)= 5 X

da,

pda, (6.57)

(s)=\x

da.

Преобразованная

по Лапласу система (6.55) приобретает вид

(0, s) = i

(6.58)

(0, s) = C

где С

, С

— константы линеаризации; y(a) = v в «окне» воз-

растов репродуктивности (р, Р + б) и равно нулю вне этого ин-

тервала.

Решая

уравнения (6.58) для паразита, после интегрирования

получим

Р (s) = G

(s)H

(s),

(6.59)

(s) = G

(s)H

(s).

226

Решая

уравнения

(6.58)

для хозяина и проинтегрировав по под-

ходящим интервалам,получим

(s)P(s),

(6.60)

где Gi(s) (г = 1, ... 7)— функции переноса.

Каждая из функций переноса Gi(s) (i= I, ..., 7) представляет

собой комплексную функцию оператора запаздывания

ехр[—(s

ц)а]. Для хозяина паразит Яо фактически является периодиче-

ским

внешним воздействием, его роль состоит в возбуждении по-

пуляционных волн, которые

дают

сложный резонансный спектр.

Фазовый

портрет общих численностей популяций имеет в общем

случае

вид замкнутой кривой с несколькими пересечениями. Кроме

простых резонансов, в системе возможны биения с периодом

больше резонансного периода. Модель

(6.54)

в целом хорошо соот-

ветствует

экспериментальным данным для систем «паразит—

хозяин». Так, Мэй выполнил сравнение расчетов по модели

(6.54)

с функцией поиска в форме

(6.56)

с экспериментальными дан-

ными

Барнетта по взаимодействию

между

оранжерейной белой

мушкой

Trialeurodes

vaporariorium

и ее паразитом

Encarsia

for-

mosa

[165]. Рисунок 6.14 показывает, что хорошее совпадение

экспериментальных и модельных значений наблюдалось в течение

22 генераций насекомых. Динамика системы представляла собой

усиливающиеся колебания, приводящие в конце концов к разру-

шению

системы.

Тщательное исследование проводилось для математической

модели, описывающей эксперименты Хаффекера (оса

Venturia

canescens

и ее паразит

Anagasta

kuhniella) [202, 326]. Один из

вариантов эксперимента и его модельного описания показан на

рис.

6.15. Как видно из рисунка, модель хорошо соответствует

опытным

данным. Динамические режимы модели исследовались

при

варьировании параметров v и Ь, отвечающих за поисковые воз-

можности паразита. В соответствии с экспериментальной процеду-

рой,

в качестве начального условия рассматривалась популяция,

состоящая только из взрослых самок. В отсутствие паразита по-

пуляция

хозяина постепенно эволюционировала к стабильному не-

прерывному распределению, как показано на рис. 6.16. Этот же

режим в ряде случаев наблюдается и при наличии паразита,

режим получил название «непрерывной распределенной моды ге-

нерации»— CGM (continuous generation mode). Более интерес-

ным

оказалось

другое

стабильное состояние, названное «дискрет-

ной

модой генерации» — DGM (discrete generation mode), кото-

рое и наблюдалось Хаффекером экспериментально. Если обе по-

пуляции

стартуют

с некоторого числа особей, имеющих ограничен-

ный

диапазон возрастов, то в последующем возрастной профиль

15* 227

Рис.

6.14. Сопоставление расчетов по мо-

дели (6.54),

(6.56)

с эксперименталь-

ными

данными по взаимодействию оран-

жерейной мушки

Trialeurodes

vaporario-

т'шт (Г) с ее паразитом

Encarsia

for-

mosa

(II) [165].

/ —

экспериментальные данные,

2 —

расчет

по

модели.

10 15

Генерации

Рис.

6.15. Динамика эксперименталь-

ной

системы (/) «паразит — хозяин»

(оса

Venturia

canescens

(а) и ее па-

разит

Anagasta

kuhniella

(б)) и ре-

зультаты

расчетов (2) [202].

Рис.

6.16. Эволюция популяции хо-

зяина

к стабильному возрастному

распределению в отсутствие паразита.

Первоначальные волны индуцирова-

ны

периодическим добавлением зре-

лых самок [326].

Возраст

Рис.

6.17. Стробоскопическое изобра-

жение с периодом 51 сутки (время

генерации хозяина) возрастного про-

филя

популяции хозяина.

Первоначальный импульс переходит

в ста-

бильное периодическое распределение [326].

Режим «дискретная мода генерации».

поддерживает эту конфигурацию (рис.

6.17).

Импульс проходит

через генерацию, так что периодический осмотр каждой генерации

дает

стабильное конечное возрастное распределение. Паразит,

имеющий

время генерации примерно в два раза меньше, чем хо-

зяин,

дает

также стабильное рас-

пределение типа DGM, состоящее

из

движущихся в противополож-

ных направлениях волновых про-

филей.

Таким образом,

хотя

вся

система имеет период 51 день,

каждый 25-й день возрастной про-

филь

паразитов конденсируется

бимодальный движущийся вол- '

новой

профиль, как показано на

Рис.

6.18. Стробоскопическое изображе-

ние

с периодом 25 сут (время генерации

паразита) возрастного профиля генера-

ции

паразита.

Первоначальный импульс переходит

в ста-

бильное периодическое распределение. Режим

Режим «дискретная мода генерации:».

Возраст

рис.

6.18. Такая бимодальная

структура

наблюдалась эксперимен-

тально Хаффекером и была им названа термином «когенерация».

Результирующий предельный цикл на фазовой плоскости

Популяция

хозяина

Рис.

6.19. Динамика общих численностей паразита и хозяина (а) и

изображение процесса на фазовой плоскости (б) [202, 326].

(рис.

6.19) имеет одно пересечение из-за присутствия

двух

волн

паразита на одну генерацию хозяина. Таким образом, в фазовом

пространстве

существуют

два состояния — одно стационарное, дру-

гое в виде движущихся волн. Как показано в работе [165], эти

два состояния

обладают

противоположной чувствительностью

изменениям параметров.

229

Чувствительность решений к малым вариациям параметров за-

дается коэффициентами чувствительности, определенными как

[280, 318]

a*(/

) =

-^-(/,

г, я),

(6.61).

где

я —

любой исследуемый параметр (например,

v или Ь).

Набор

уравнений

для

эволюции коэффициентов чувствительно-

сти можно получить, дифференцируя уравнения модели

(6.55)

no-

параметрам

я.

Полученные уравнения имеют

вид

~dt

«o + V

n(0,t)= j m

da+ J

-^-pda,

(6.62)-

К , К

Л ^ аа

•о*

(0,/)=

Чувствительность популяций к изменению параметров можно полу-

чить, интегрируя по всем возрастам и затем дифференцируя по-

параметрам:

<*л

(t) = §(т

—

)

da — \ —^- р da,

(6.63)

оо

а* (0= J im

-li

)aUa+\-^-h

da.

В целом уравнения чувствительности имеют ту же форму, что и

линеаризованные

уравнения для анализа устойчивости, но с реше-

нием

первоначальной модели в качестве вынуждающей силы.

Исследование чувствительности модели к вариациям параметра

поиска

v у паразита

дает

достаточно неожиданные результаты —

режиме дискретных мод с увеличением стационарной плотности

хозяина плотность паразида уменьшается, в режиме непрерывных

мод — наоборот. Таким образом, коэффициенты чувствительности

оь и оь меняют знак при переходе от одного режима к

другому.

Экспериментальное подтверждение изменения знака чувствитель-

ности

при смене динамических режимов дано в работе [326].

230