Акрамова Н.П. Инженерная графика конспект лекций

Подождите немного. Документ загружается.

Министерство образования и науки Украины

Приазовский государственный технический университет

ИНЖЕНЕРНАЯ ГРАФИКА

Конспект лекций для студентов

групп МА, МЧ и МС

Акрамова Н. П. ст. преп.

Ковалевский И. А. доц. к. т. н.

Кондрашин С. Е. доц. к. т. н.

Отрощенко н. н. ст. преп.

Филатов В. В. ст. преп.

Мариуполь 2008

УДК 681.5.017

Инженерная графика

Мариуполь: ПГТУ, 2008, - 48 стр., 69 ил.

Конспект лекций для студентов групп МА, МЧ и МС.

Составили:

Ст. преп. Акрамова Н.П., доц.. Кондрашин С.Е., доц. Ковалевский И.А.,

ст.пр. Отрощенко Н.Н., ст.пр. Филатов В.В.

Рецензент: Ковалевский И.А., доц.

Ответственный за выпуск :

Зав. кафедрой Ковалевский И.А., доц.

Утверждено на заседании кафедры Утверждено методической комиссией

графики и начертательной геометрии Сварочного факультета

протокол № 9 от 22.05.08 протокол № 9 от 30. 03. 09

ОГЛАВЛЕНИЕ

Лекция 1

1.1. МЕТОДЫ ПРОЕЦИРОВАНИЯ…………………………………………………………………………5

1.1.1.Центральное проецирование………………………………………………………...5

1.1.2.Параллельное и ортогональное проецирование……………………………………5

1.1.3.Свойства ортогонального проецирования………………………………………….5

1.1.4.Обратимость чертежа………………………………………………………………...6

1.2. ТРЁХКАРТИННЫЙ ЧЕРТЕЖ ТОЧКИ……………………………………………………...7

1.2.1.Аппарат проецирования……………………………………………………………..7

1.2.2.Конкурирующие точки……………………………………………………………….8

Лекция 2

2. ЧЕРТЕЖ ПРЯМОЙ………………………………………………………………………...9

2.1.Положение прямой относительно плоскостей проекций………………………….9

2.1.1.Прямая общего положения………………………………………………………9

2.1.2.Прямая уровня……………………………………………………………………9

2.1.3.Проецирующая прямая………………………………………………………….10

2.2.Взаимное положение прямых……………………………………………………....12

Лекция 3

3. КОМПЛЕКСНЫЙ ЧЕРТЕЖ ПЛОСКОСТИ...........................................................................13

3.1.Положение плоскости относительно плоскостей проекций………………….…...13

3.1.1.Плоскость общего положения……………………………………………….…..13

3.1.2.Проецирующая плоскость……………………………………………………….14

3.1.3.Плоскость уровня………………………………………………………………...14

3.2.Принадлежность прямой и точки плоскости…………………………………….....15

3.3.Прямые особого положении в плоскости…………………………………………..16

3.3.1.Прямая уровня плоскости…………………………………………......................16

Лекция 4

4.1. ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ, ДВУХ ПЛОСКОСТЕЙ……………18

4.1.1.Параллельность прямой и плоскости…………………………………………….....18

4.1.2.Параллельность плоскостей…………………………………………………………18

4.1.3.Пересечение прямой и плоскости…………………………………………………..19

4.1.3.1.Пересечение прямой и плоскости частного положения……………………....19

4.1.3.2.Пересечение плоскости с плоскостью частного положения………………….19

4. 2.СПОСОБЫ ПРЕОБРАЗОВАНИЯ ЧЕРТЕЖА…………………………………………….....20

4.2.1.Замена плоскостей проекций………………………………………………………..20

Лекция 5

5. МНОГОГРАННИКИ…………………………………………………………………….…..23

5.1.Изображения многогранника на комплексном чертеже…………………………....23

5.2.Пересечение многогранника плоскостью…………………………………………...24

5.3.Пересечение многогранника прямой……………………………………………..….25

5.4.Взаимное пересечение многогранников……………………………………………..25

Лекция 6

6.1. КРИВЫЕ ЛИНИИ………………………………………………………………………….28

6.1.1.Основные свойства проекций плоских кривых линий…………………………….28

6.1.2.Проецирование окружности…………………………………………………………28

6.1.3.Цилиндрическая винтовая линия……………………………………………………29

6.2. КРИВОЛИНЕЙНЫЕ ПОВЕРХНОСТИ……………………………………………………...30

6.2.1.Очерк поверхности…………………………………………………………………...30

6.3. ПОВЕРХНОСТИ ВРАЩЕНИЯ………………………………………………………………31

6.3.1.Основные линии поверхности вращения……………………………………………31

Лекция 7(продолжение)

7.1.Очерковые образующие и точка на поверхности цилиндра………………………..32

7.2. Очерковые образующие и точка на поверхности конуса………………………….32

7.3. Очерковые образующие и точка на поверхности сферы…………………………..33

7.4.Пересечение криволинейной поверхности плоскостью………………………........33

7.4.1. Цилиндрические сечения……………………………………………………........33

7.4.2. Конические сечения……………………………………………………………….34

7.4.3. Сферические сечения……………………………………………………………...34

7.5.Построение сечения поверхности вращения плоскостью…………………………...35

7.6.Пересечение поверхности прямой линией……………………………………………37

Лекция 8

8. ВЗАИМНОЕ ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ …………………………………………….38

8.1.Пересечение криволинейной и гранной поверхностей………………………………38

8.2.Пересечение поверхностей вращения второго порядка……………………………..40

8.2.1.Способ секущих плоскостей……………………....................................................40

8.2.2.Особые случаи пересечения поверхностей вращения второго порядка………..41

Лекция 9

9. РАЗВЕРТКИ ПОВЕРХНОСТЕЙ……………………………………………………………..43

9.1.Развертка призмы……………………………………………………………………..43

9.2.Развертка пирамиды……………………………………………………………….….44

9.3.Развертки криволинейных поверхностей…………………………………………....45

9.3.1. Развертка цилиндрической поверхности…………………………………….…46

9.3.2. Развертка конической поверхности……………………………………………..47

Лекция 1

1.1. МЕТОДЫ ПРОЕЦИРОВАНИЯ

Для построения чертежа применяются различные методы проецирования.

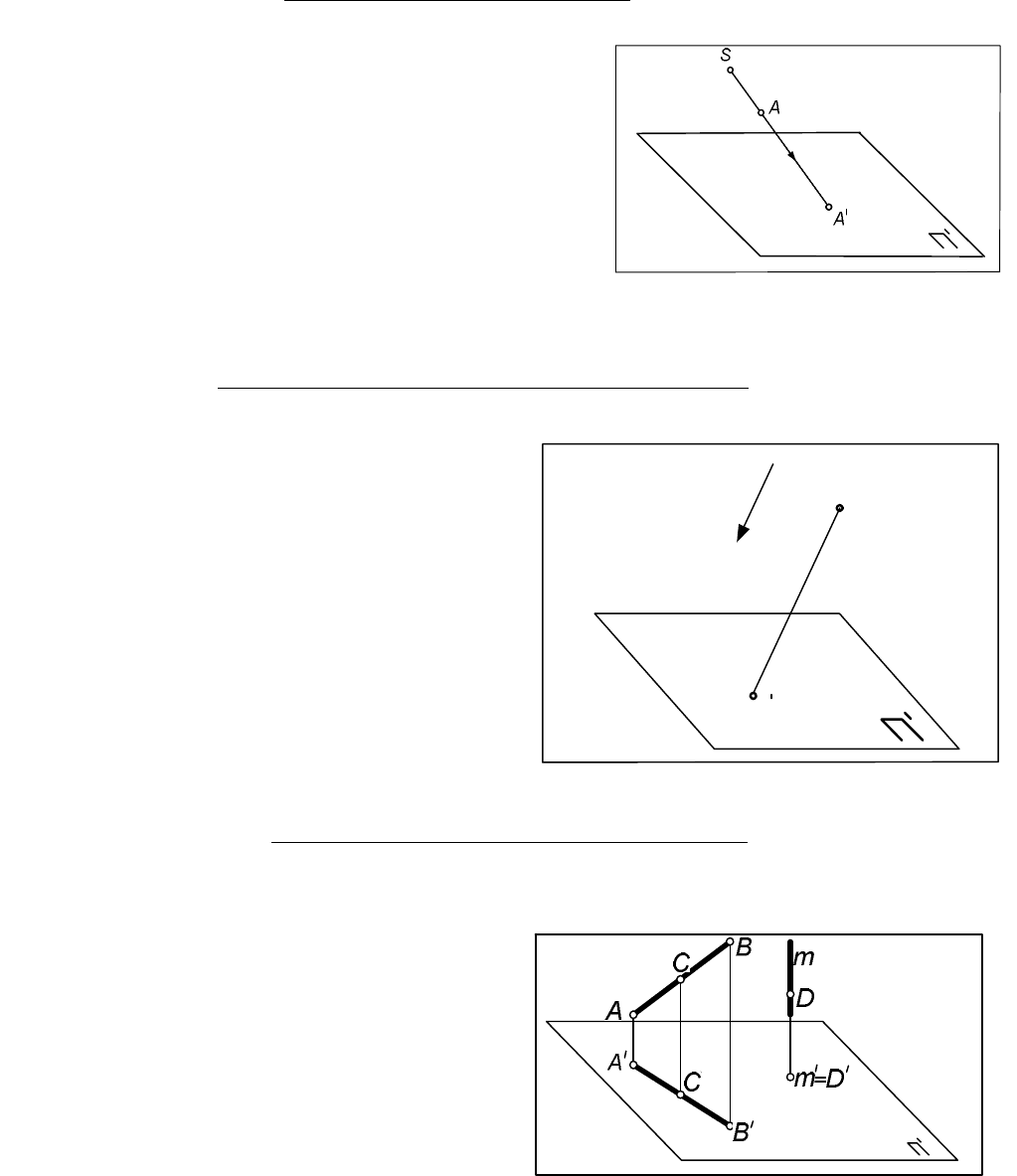
1.1.1.Центральное проецирование

В аппарат центрального проецирования (параметры,

выбираемые проектировщиком) входят:

 плоскость проекций П',

 центр проекций S.

Чтобы построить центральную проекцию точки А

пространства, нужно через центр S и точку А провести

прямую, называемую проецирующей. Точка

пересечения проецирующей прямой с плоскостью

проекций и будет центральной проекцией точки А -

А'.

Рис.1

1.1.2.Параллельное и ортогональное проецирование

Аппарат параллельного проецирования:

 плоскость проекций П

 направление проецирования s.

Чтобы построить параллельную проекцию

точки А пространства, нужно через точку А

провести проецирующую прямую,

параллельную s. Точка пересечения

проецирующей прямой с плоскостью проекций

и будет параллельной проекцией точки А - А'.

Если направление проецирования

перпендикулярно плоскости проекций, то такое

проецирование называется ортогональ

ным.

Рис.2

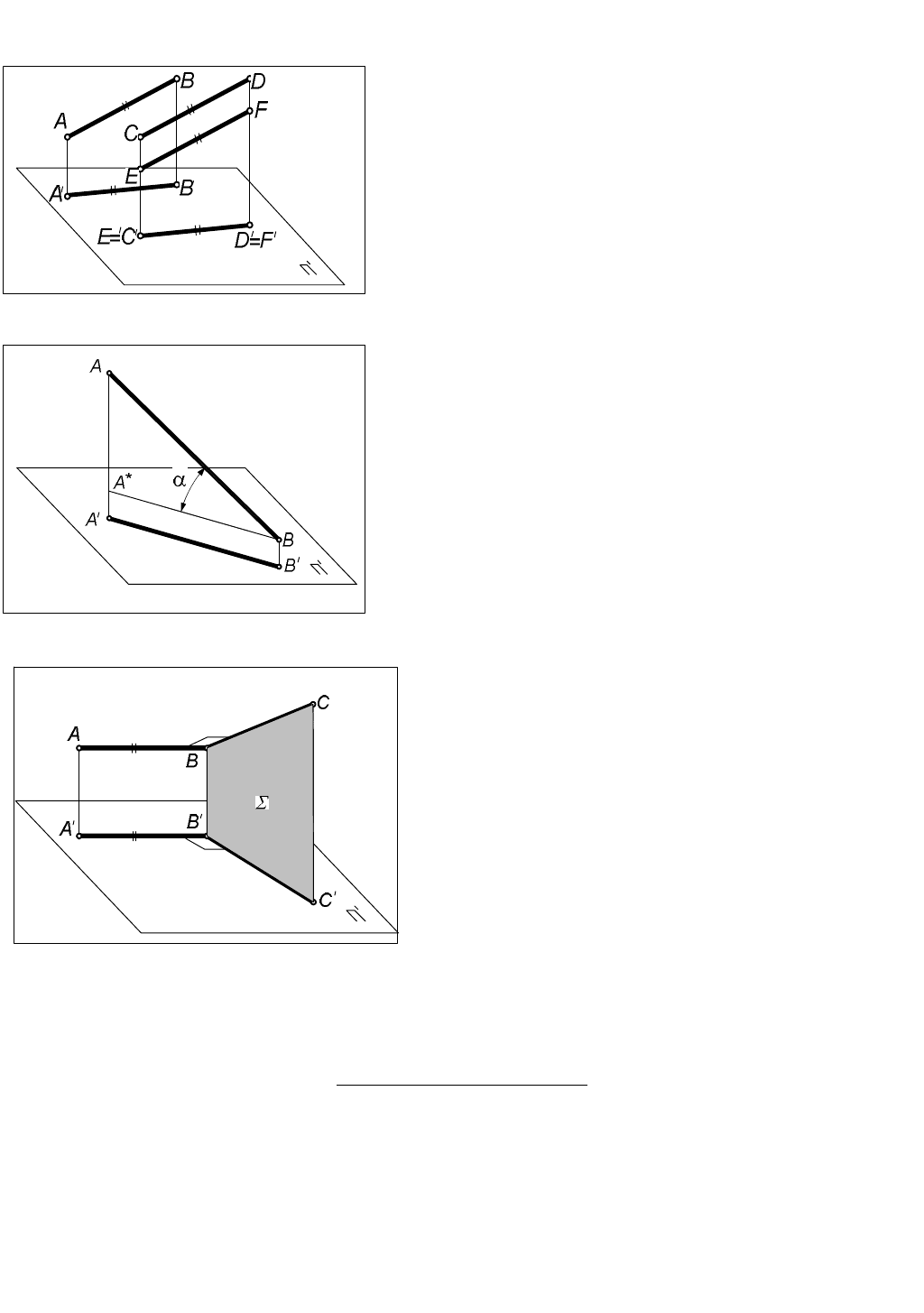
1.1.3.Свойства ортогонального проецирования

1. Проекцией точки является точка.

2. Проекцией прямой, не перпендикулярной

плоскости проекций, является прямая

(рис.3).

3. Если точка принадлежит прямой, то

проекция точки принадлежит проекции

прямой (рис.3).

4. Если прямые параллельны, то их

проекции параллельны или совпадают

(рис.4).

Рис.3

Рис. 4

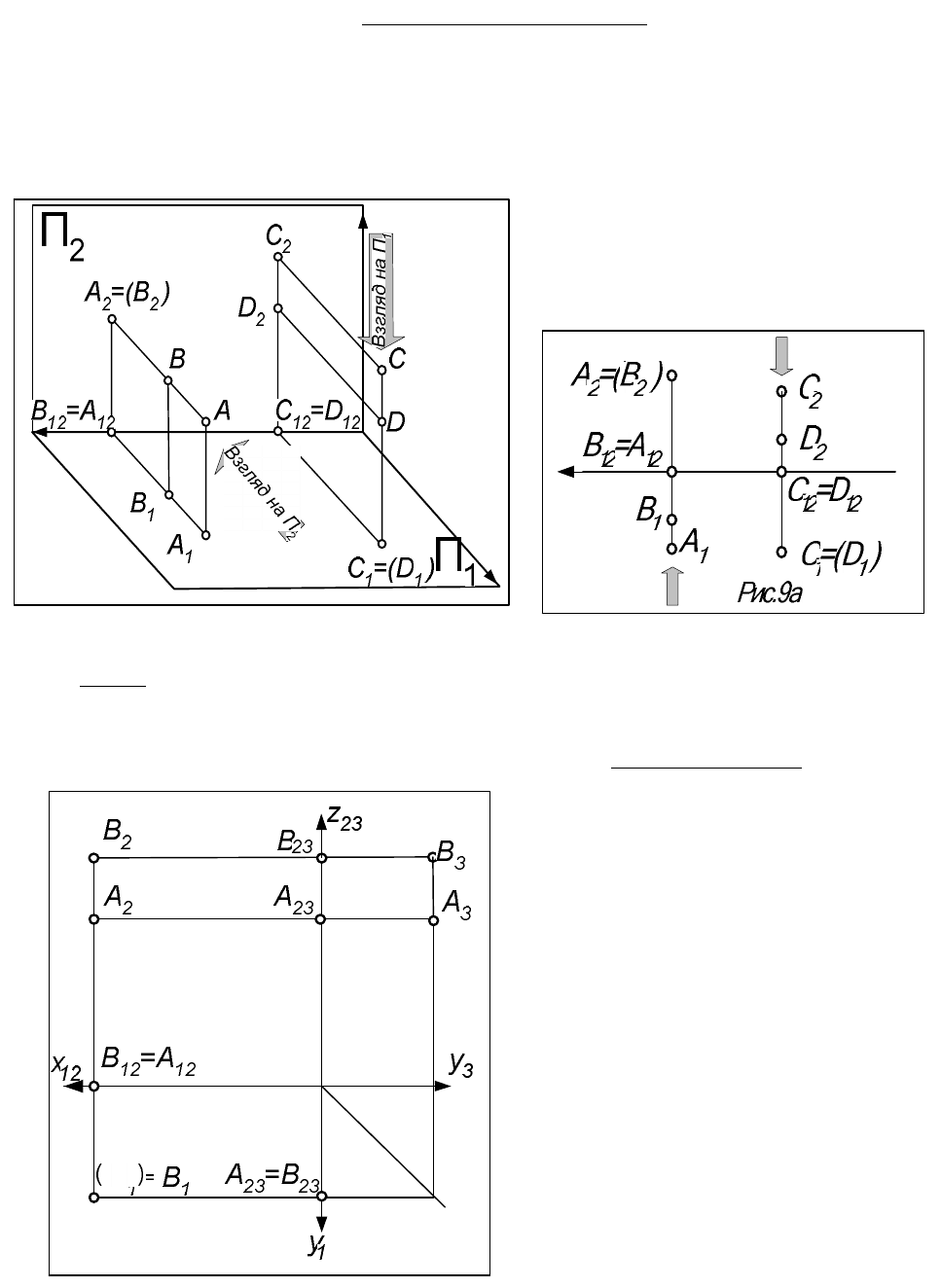
5. Отношение отрезков, лежащих на одной

прямой или на параллельных прямых, равно

отношению проекций этих отрезков: [АС]:[ВС]

= [A'C']:[В'С'] (рис.3.)

Рис. 5

6. Длина проекции отрезка, наклонного к

плоскости проекций, меньше длины отрезка в

пространстве и равна [A

] = [AB]? Cos α

(рис.5), что следует из треугольника АВА*.

Рис.6

7.Если одна сторона прямого угла параллельна

плоскости проекций, а дру-гaя к ней не

перпендикулярна, то прямой угол проецируется в

натуральную величину (рис.6):

если прямая перпендикулярна двум

пересекающимся прямым плоскости



, то она

перпендикулярна этой плоскости и любой прямой

ей принадлежащей:

(АВ)(ВС) и (АВ)(ВВ

), то (АВ)



(А

)║(АВ), следовательно(А

)



(В

).(А

)

8. Проекция фигуры не изменится при параллельном переносе плоскости проекций.

1.1.4.Обратимость чертежа

Проекции точки А' (рис.2) соответствует бесконечное множество точек А в

пространстве, расположенных на проецирующей прямой АА', т.е. реконструировать однозначно

точку в пространстве невозможно и такой чертеж не обладает свойством обратимости.

Впервые задачу создания обратимого (комплексного) чертежа решил французский учёный

Гаспар Монж, предложивший ортогонально проецировать точку на две и более взаимно

перпендикулярных плоскости проекций. Стандартом Единой системы конструкторской

документации (ЕСКД) установлено 6 основных плоскостей проекций, образующих грани куба.

1.2. ТРЁХКАРТИННЫЙ ЧЕРТЕЖ ТОЧКИ

1.2.1Аппарат проецирования

Плоскости проекций:

 П

– горизонтальная,

 П

– фронтальная,

 П

– профильная.

Оси проекций: x

, y

13,

Чтобы построить чертеж точки,

методом ортогонального проецирования

находятся последовательно проекции

точки: А

– горизонтальная, А

–

фронтальная, А

– профильная, а также

, А

– проекции точки на осях

проекций.

Параметры точки: высота h, глубина f,

широта р – расстояния от точки до

горизонтальной, фронтальной и

профильной плоскости проекций

соответственно.

Рис.7

Для получения плоского изображения (чертежа) пространственную конструкцию из плоскостей

проекций мысленно разрезаем по оси y

, П

вращаем вокруг оси x

вниз от наблюдателя до

совмещения с П

, а П

вращаем вокруг оси z

вправо от наблюдателя до совмещения с П

, как

это показано на рис.7.

. Ломаные линии А

, А

превращаются в прямые,

перпендикулярные соответствующим

осям проекций и называемые линиями

связи.

Для удобства построений проведем

константу К

чертежа под 45

к осям

проекций через точку их пересечения.

Тогда трёхкартинный чертеж точки

представит собой прямоугольник,

стороны которого – линии связи,

перпендикулярные соответствующим

осям проекций; три вершины

прямоугольника – проекции точки, а

четвертая – точка перелома линии

связи на константе комплексного

чертежа К

(рис.8)

Рис.8

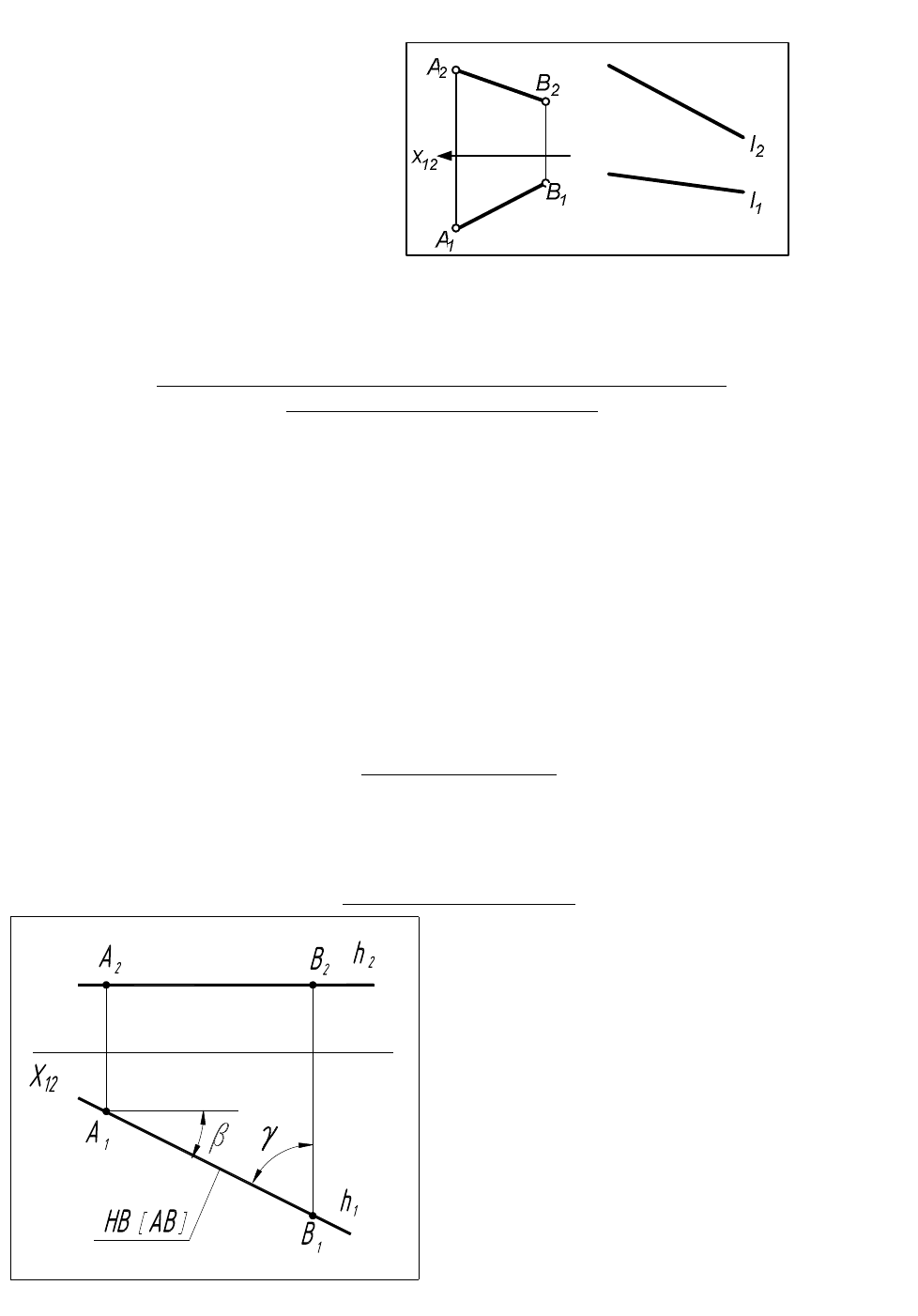
1.2.2.Конкурирующие точки

Определение – точки, лежащие на одной прямой, перпендикулярной какой-либо плоскости

проекций (рис.9). Они конкурируют в видимости на той плоскости проекций, к которой

ортогональна проецирующая прямая.

Признак: проекции конкурирующих точек проекции совпадают в той плоскости, в которой

они конкурируют в видимости (рис.9, 9а).

Рис.9

Для определения видимости

точек рассматривается их чертеж

совместно с направлением взгляда на

плоскость конкуренции.

Задача. Построить чертеж точки А (40,20,30) и горизонтально конкурирующую с

ней точку В и видимую на П

. (рис.10).

Алгоритм решения:

1. Строим проекции точки А

на осях проекций, откладывая

соответствующей длины

координатные отрезки.

2. Через построенные проекции

проводим линии связи,

перпендикулярные осям, на которых

эти проекции расположены.

3. В точках пересечения линий

связи отмечаем проекции точки А на

плоскостях проекций А

, А

и А

4. Строим проекции точки В :

 т.к. А и В – горизонтально

конкурирующие, то А

=В

;

 т.к. В видима на П

, то она

ближе расположена к наблюдателю ,

чем точка А и имеет большую высоту.

Невидимую точку берем в скобки.

Рис.10

Лекция 2

2. ЧЕРТЕЖ ПРЯМОЙ

В пространстве прямая задаётся

двумя своими точками или точкой и

направлением. На чертеже прямая

задается своими проекциями: либо

проекциями отрезка, либо участка

прямой без указания ей

принадлежащих точек (рис.11).

На чертеже прямой l не указаны

ни линии связи, ни ось проекций

(безосный чертеж).

Рис.11

В случае необходимости ось может быть проведена в любом месте чертежа при одном

условии – она должна быть горизонтальна.

2.1.Положение прямой относительно плоскостей проекций

2.1.1.Прямая общего положения

Определение - наклонена ко всем плоскостям проекций

Признак: проекции прямой наклонены к осям проекций (рис.11).

Свойства чертежа: отрезок прямой и углы наклона прямой к плоскостям проекций про-

ецируются на плоскости проекций с искажением.

По чертежу легко можно представить, какое положение занимает прямая в пространстве

относительно плоскостей проекций. Точка А находится к наблюдателю ближе, чем точка

В и расположена выше (рис. 11). У этой прямой высота точек по мере удаления от

наблюдателя уменьшается. Такая прямая называется нисходящей.

Признак: у нисходящей прямой проекции наклонены в разные стороны.

У прямой l, изображенной на рис.11, по мере удаления от наблюдателя высота точек

увеличивается. Такая прямая называется восходящей.

Признак: у восходящей прямой проекции ориентированы одинаково.

2.1.2.Прямая уровня

Определение – параллельна какой-либо плоскости проекций.

Признак – проекция прямой уровня в непараллельную плоскость – параллельна оси проекций.

Свойства чертежа – в параллельную плоскость проекций отрезок прямой и углы наклона её

к плоскостям проекций проецируются в натуральную величину.

Горизонтальная прямая.

Определение - горизонтальной прямой

называется прямая, параллельная

горизонтальной плоскости проекций.

На комплексном чертеже обозначается h.

Такое обозначение подчеркивает, что для всех

точек прямой координата h (высота) – Const.

Признак – фронтальная проекция h

располагается параллельно оси Х (рис.12).

Для построения фронтальной проекции

горизонтали достаточно знать проекцию одной

точки.

a – угол с П

; a = 0

b – угол с П

g – угол с П

Рис.12

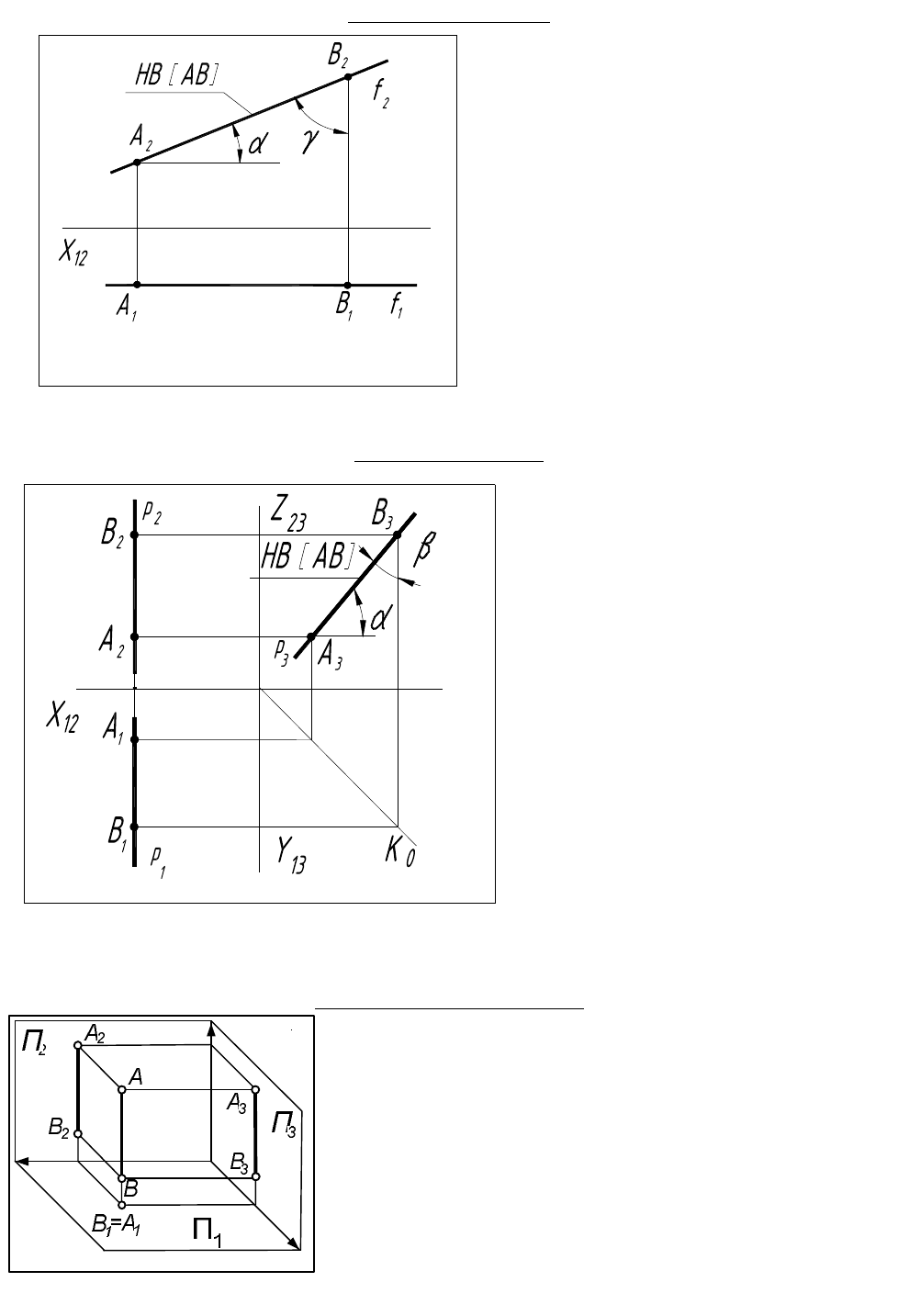
Фронтальная прямая.

Определение – фронтальной прямой

называется прямая, параллельная

фронтальной плоскости проекций.

На комплексном чертеже обозначается f.

Для всех точек прямой координата

f (глубина) – Const.

Признак – горизонтальная проекция f

располагается параллельно оси Х

(рис.13).

b=0

Для построения горизонтальной

проекции фронтали достаточно знать

проекцию одной точки.

Рис.13

Профильная прямая

Определение – профильной

прямой называется прямая,

параллельная профильной

плоскости проекций.

На комплексном чертеже

обозначается p.

Для всех точек прямой

координата

P (широта) – Const.

Признак – фронтальная и

горизонтальная проекции

прямой располагаются

параллельно осям Z и Y

(рис.14).

g =0

Рис.14

2.1.3.Проецирующая прямая

Рис.15

Определение – прямая, перпендикулярная

какой-либо плоскости проекций.

Признак – проекция прямой в

перпендикулярную плоскость – точка, в

параллельные – прямые перпендикулярные

соответствующим осям проекций (рис.15).

Свойства чертежа – в параллельную

плоскость проекций отрезок прямой

проецируется в натуральную величину.