Акрамова Н.П. Инженерная графика конспект лекций
Подождите немного. Документ загружается.

41
Рис.64
3. Случайные
точки ЛП находим
тем же способом,
что и точки 3 и 4,
проводя
горизонтальные
секущие плоскости
и
. При этом для
упрощения
построений
проводим их на
одинаковом
расстоянии от
экватора n (тогда
r
= r
.).
4. Видимость ЛП
и очерков
поверхностей
определяем по
представлению.
11.2.2.Особые случаи пересечения поверхностей вращения второго порядка
В общем случае поверхности вращения 2-го порядка пересекаются по
пространственным кривым 4-го порядка. Существуют частные случаи, когда такие
поверхности пересекаются по плоским кривым второго порядка.
С одним таким случаем - соосными поверхностями - мы познакомились выше.
Другие признаки распадения кривой 4-го порядка на плоские кривые 2-го порядка
сформулированы в следующих теоремах.
Теорема о двойном прикосновении: если две пересекающиеся поверхности
вращения 2-го порядка имеют две точки касания, то линия их пересечения распадается на
две плоские кривые 2-го порядка, плоскости которых проходят через прямую,
соединяющую точки касания.
5
6
7
8
1
=
1
6
R
R
2
2
Г
r
r
r
r
r
R
R
R
R
Г
r
1
2
2
2
4
1
1
1
3
1
2
1
3
2
4
=
2
5
2
=
2
2
=
2
7
1
8
1
O
1
O
2
S
S
1
2
Г
2
n
=
2
n
1
m
1
m
2
А
А
1
2
В
2
В
1
на П
1
42
Под точкой касания поверхностей понимается такая их общая точка, через
которую можно провести плоскость, касательную к обеим поверхностям.
Теорема Монжа: если две пересекающиеся поверхности 2-го порядка описаны
около третьей поверхности 2-го порядка или вписаны в нее, то линия их пересечения
распадается на две плоские кривые 2-го порядка, плоскости которых проходят через
прямую, соединяющую точки пересечения линий касания поверхностей.
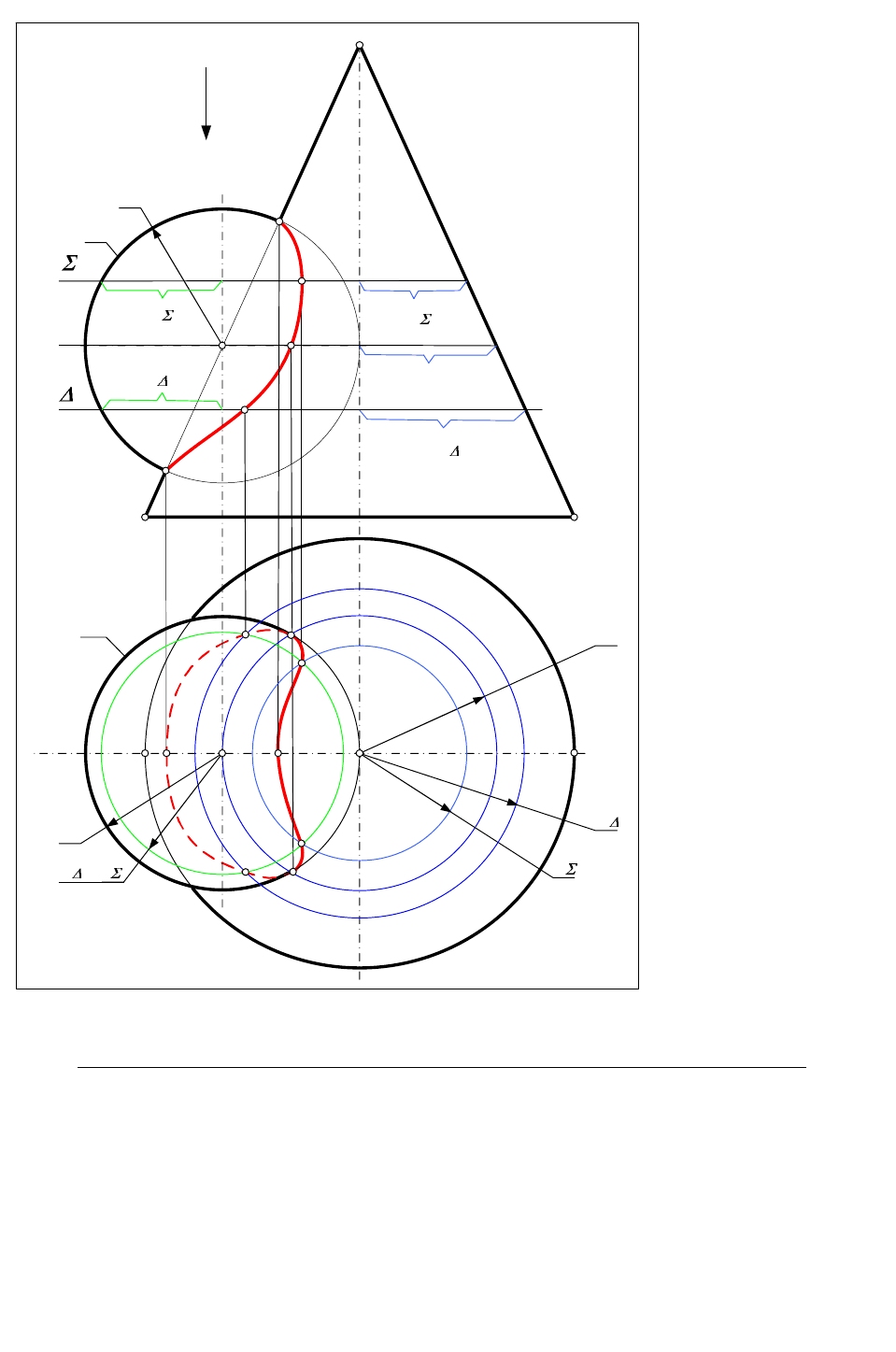
Рис.65
На рис.65 показаны два цилиндра
вращения, описанные вокруг сферы радиуса
r. По теореме Монжа они имеют две точки
касания А = e l и В = f k, через которые
можно провести фронтальные плоскости
(
1
) и
*
(
1
*
), касающиеся обеих цилиндров
по образующим e, f и k, l. На П
2
проекции
точек А и В, найденные по принадлежности
образующим e и f, совпадают (A
2
= B
2
), то
есть отрезок (АВ) – фронтально
проецирующий, и плоскости кривых, по
которым пересекаются цилиндры, также
фронтально проецирующие и проецируются
на П
2
в виде отрезков, проходящих через A
2
= B
2
. Для построения этих отрезков
достаточно построить еще две пары точек,
принадлежащих обоим цилиндрам. Это
точки пересечения фронтальных
очерковых, лежащих в одной фронтальной
плоскости Ф(Ф
1
): 1
2
= m
2
c
2
, 2
2
=
m
2
d
2
, 3
2
= n
2
c
2
, 4
2
= n
2
d
2
.
Cоединив попарно точки 1
2
и 4
2
, 2
2
и 3
2
отрезками, получим проекции ЛП цилиндров -
двух плоских кривых второго порядка. Т.к. плоскости их наклонены к осям цилиндров, то
это эллипсы. На П
1
эллипсы проецируются на окружность – вырожденную проекцию
горизонтально проецирующего цилиндра.
43
Лекция 9
12.РАЗВЕРТКИ ПОВЕРХНОСТЕЙ.
Разверткой называется фигура, полученная совмещением с плоскостью без
складок и разрывов гранной или криволинейной поверхности, которые можно
представить себе как гибкую нерастяжимую пленку. Не все поверхности являются
развертываемыми. К последним относятся гранные поверхности, цилиндр, конус и
торс, а все остальные криволинейной поверхности можно развернуть только
приближенно, заменяя (аппроксимируя) развертывающимися поверхностями.
12.1.Развертка призмы
Развертка призмы представляет собой фигуру, состоящую из натуральной
величины боковых граней и обоих оснований. Мысленно разрезав многогранник по
одному из боковых ребер и ребрам оснований, вращением вокруг остальных ребер
последовательно совмещаем все грани с плоскостью проекций.
Для построения развертки призмы необходимо знать натуральные величины ребер
призмы и нормального сечения. Нормальным называется сечение призмы плоскостью,
перпендикулярной боковым ребрам. При развертывании боковой поверхности призмы
нормальное сечение разворачивается в прямую, перпендикулярную проекциям боковых
ребер на развертке.
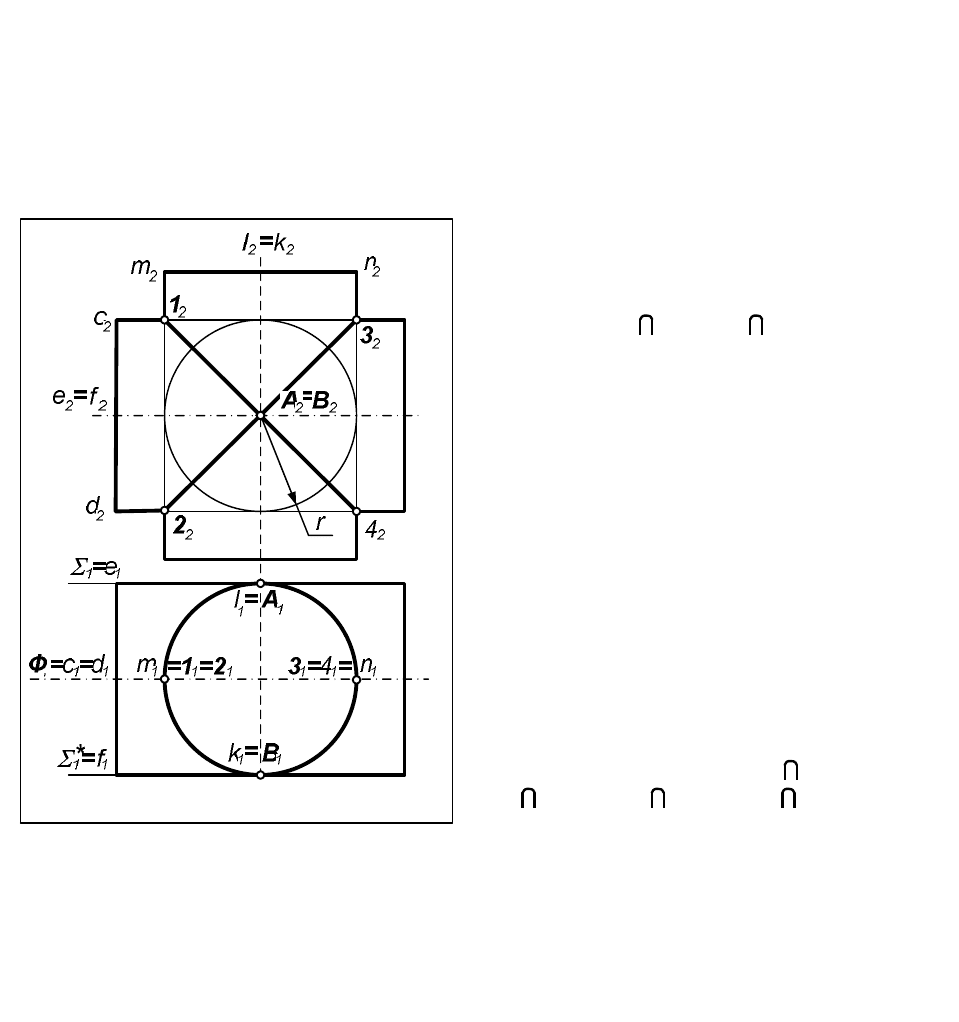
Задача. Построить развертку прямой треугольной усеченной призмы (рис.66).
Рис.66
Т.к. призма прямая, то основание ее будет нормальным сечением, которое на П
1

44
проецируется в натуральную величину. Ребра призмы – фронтальные прямые, следова-
тельно, на П
2
они проецируются в натуральную величину. Таким образом, все
необходимые данные для построения развертки уже имеются на чертеже.
Алгоритм построения развертки:
12. Строим развертку боковой поверхности усеченной призмы.
На свободном поле чертежа ( для удобства построений – в проекционной связи с фрон-
тальной проекцией нижнего основания) строим развертку нормального сечения
(основания) – проводим прямую, на которой откладываем НВ ребер основания, взяв их с
горизонтальной проекции – [АВ] = [А
1
В
1
] и т.д.
Через построенные на развертке вершины основания проводим прямые, перпендику-
лярные развертке основания, и откладываем на них НВ боковых ребер и отрезков,
отсекаемых на них секущей плоскостью
; если развертка строится в проекционной
связи с фронтальной проекцией призмы (как на рис.66), то для этого достаточно провести
горизонтальные линии связи до пересечения с проекциями соответствующих ребер.
2. Пристраиваем к полученной развертке боковой поверхности НВ основания и
сечения, строя их по их трем известным сторонам (методом триангуляции). Для
построения НВ сечения выбираем в качестве исходной его сторону (23), и из точек 2
и 3 проводим дуги окружностей, радиусы которых равны соответственно [12] и [13].
Точка пересечения этих дуг и есть вершина А сечения. Аналогично строим НВ
основания.
12.2.Развертка пирамиды.
Построение развертки пирамиды сводится к многократному построению методом
триангуляции натуральных величин треугольников, из которых состоит боковая
поверхность пирамиды, плюс НВ основания. Для этого необходимо знать НВ всех ребер
пирамиды.
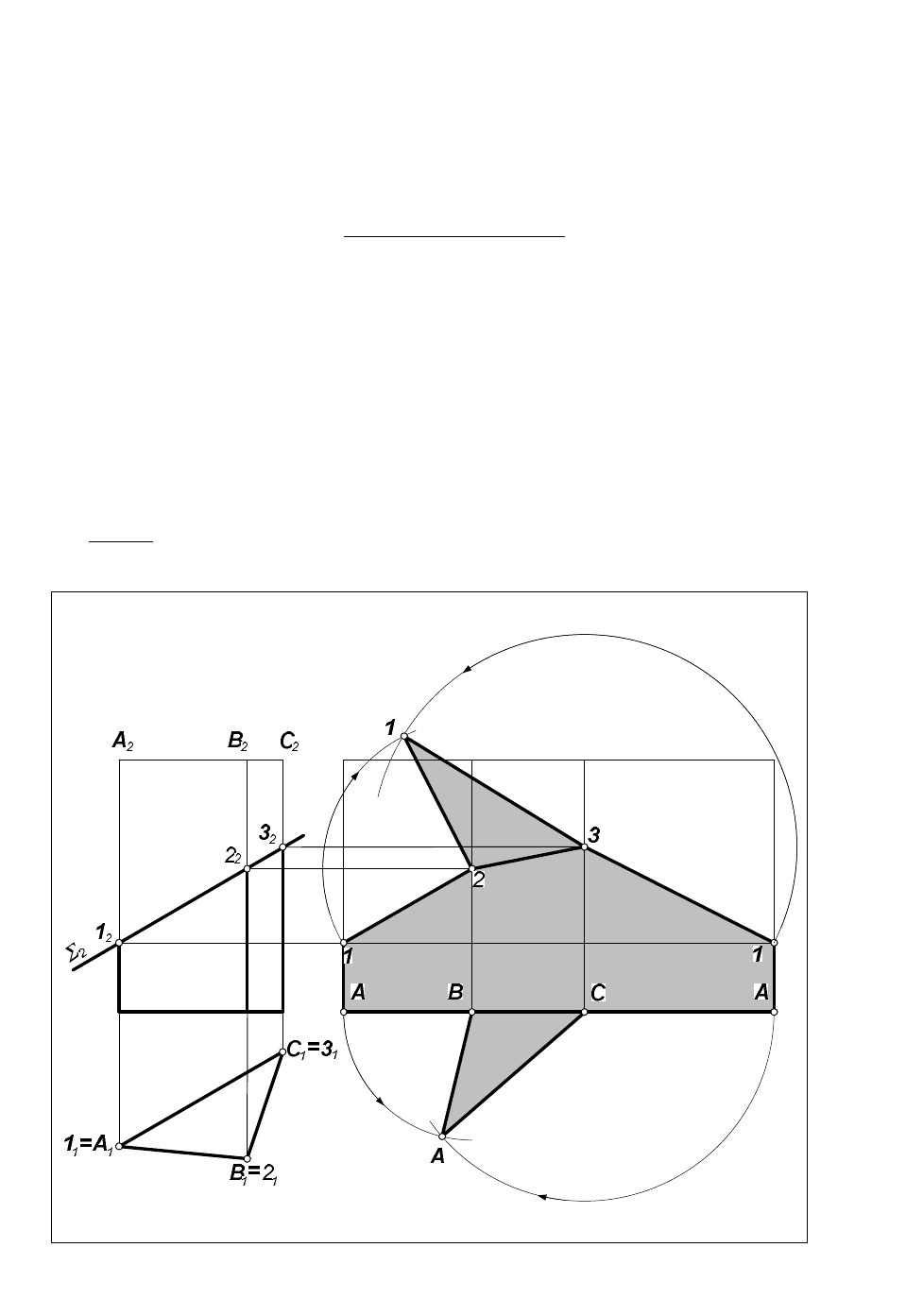
Задача. Построить развертку усеченной пирамиды (рис.67).
Алгоритм решения
1. Определяем НВ ребер пирамиды.
Основание АВС параллельно П
1
, поэтому ребра основания проецируются в П
1
в
натуральную величину.
Боковые ребра пирамиды – общего положения и для определения их НВ применяем
метод вращения вокруг горизонтально проецирующей прямой i, проходящей через
вершину пирамиды S. При вращении вокруг оси i точки А, В и С описывают окружности
плоскости, которых перпендикулярны оси. В П
1
эти окружности проецируются в НВ с
центром в i
1
, а на П
2
– в виде отрезков, перпендикулярных i
2
. Поворачиваем
горизонтальные проекции боковых ребер до параллельности оси проекций x
12
. Тогда в
пространстве ребра расположатся параллельно П
2
и спроецируются в эту плоскость в НВ.
Находим проекции точек А, В и С в нужном нам положении (А
2
*
, В
2
*
, С
2
*
) как результат
пересечения линий связи, проведенных через А
1
*
, В
1
*
, С
1
*
и траекторией перемещения
фронтальных проекций точек А, В и С. Отрезки S
2
А
2
*
, S
2
В
2
*
и S
2
С
2
*
натуральные
величины боковых ребер.
45
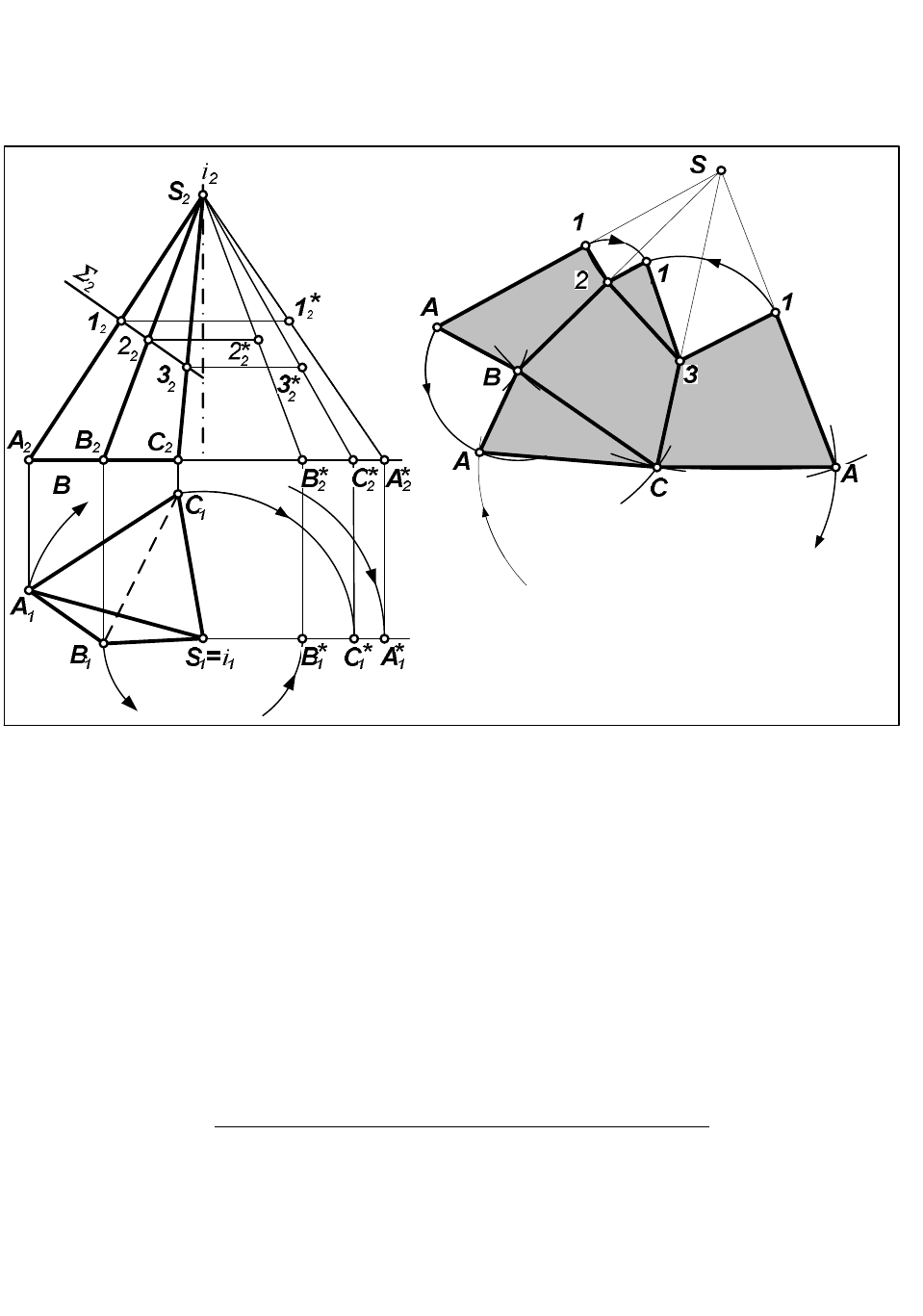
Секущая плоскость
(
2
) фронтально проецирующая и сечение проецируется на П
2
в
виде отрезка на вырожденной проекции плоскости, расположенного внутри очерка
призмы. Вершины сечения на П
2
находим как результат пересечения проекций ребер с
2
. На натуральных величинах боковых ребер точки 1
2
*
, 2
2
*
, 3
2
*
находим по принадлежности
соответствующим ребрам, проведя траектории точек при вращении ребер вокруг оси i.
Рис.67
2. Строим развертку боковой поверхности
На свободном поле чертежа проводим прямую и откладываем на ней НВ ребра SA =
S
2
А
2
*
. Методом триангуляции строим НВ грани SAB : из точки А, как из центра, проводим
дугу радиусом, равным [АВ] = [A
1
B
1
], а из точки S – дугу радиусом, равным [SB] = [S
2
В
2
*
].
Точка пересечения этих дуг – вершина В на развертке. Соединив построенные точки,
получаем НВ грани ASB. Наносим сторону (12) сечения, откладывая на стороне SA
отрезок [1S] = [S
2
1
2
*
], а на стороне SB – отрезок [2S] = [S
2
2
2
*
]. По аналогичному
алгоритму строим на развертке НВ граней BSC и ASC, нанося на них стороны сечения
(23) и (31).
3. Строим полную развертку пирамиды, пристраивая к развертке боковой поверхности НВ
основания и сечения, применяя метод триангуляции, как это показано на рис.67
12.3.Развертывание криволинейных поверхностей
Криволинейные поверхности, которые полностью, без растяжения или сжатия, без
разрывов и складок можно совместить с плоскостью, называют развертываемыми. К этим
поверхностям относятся лишь линейчатые и только такие, у которых смежные
образующие пересекаются между собой или параллельны. Этим свойством обладают
конические и цилиндрические поверхности.
46
12.3.1.Развертка цилиндрической поверхности
Развертка боковой поверхности прямого кругового цилиндра радиуса R и высотой
h представляет собой прямоугольник, одна из сторон которого равна длине 2
R
окружности основания, а другая высоте h цилиндра.
Если цилиндр прямой усеченный или наклонный, строится приближенная
развертка: в цилиндр вписывается n-угольная призма и строится ее развертка.
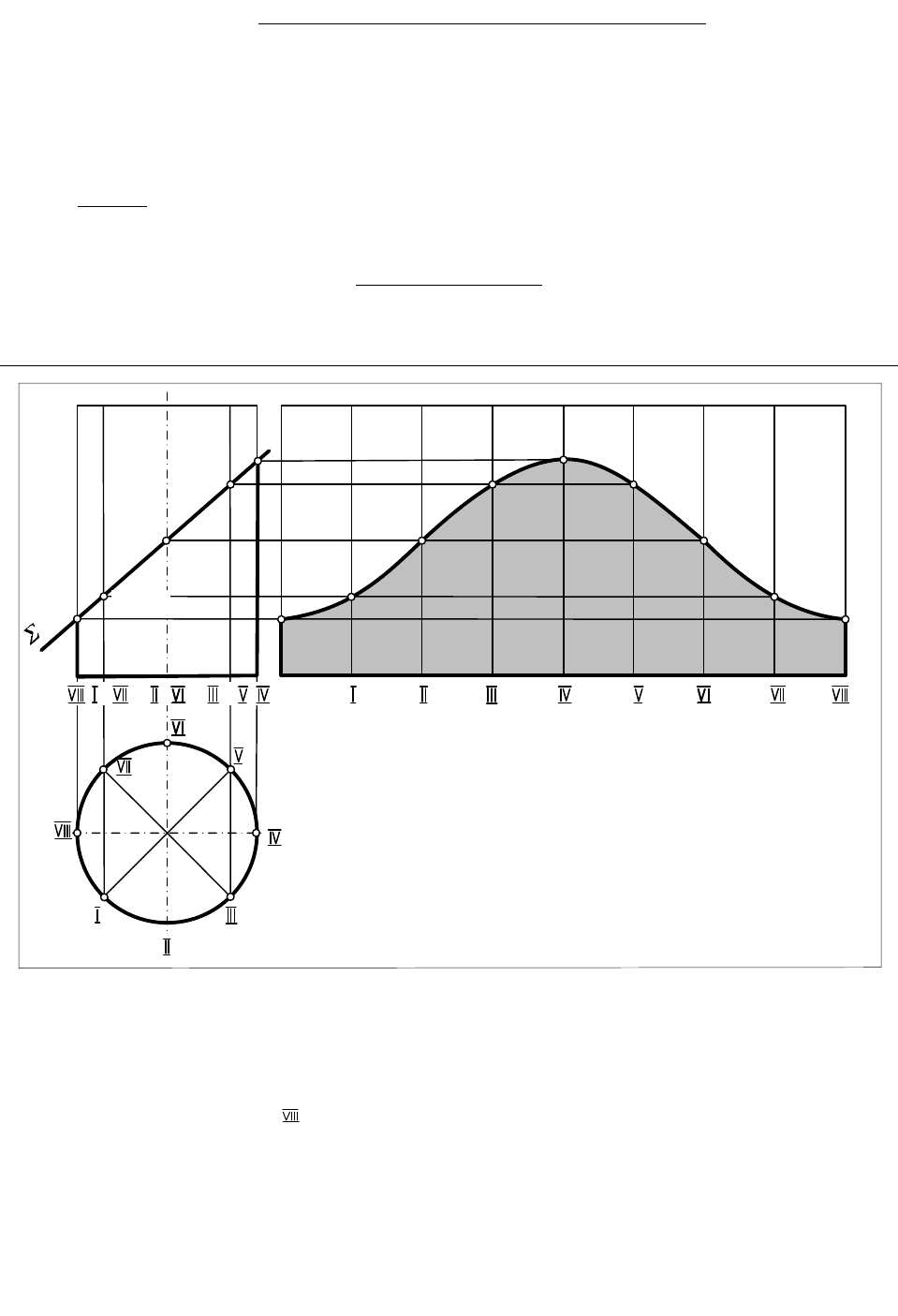
Задача. Построить развертку боковой поверхности прямого кругового цилиндра,
усеченного плоскостью
(рис.68).
Алгоритм решения
1. Строим развертку боковой поверхности цилиндра в проекционной связи с его
фронтальной проекцией (для удобства построений).
Рис.68
2. В цилиндр вписываем n-угольную (на рис.68 – 8 угольную) правильную призму
и строим её развертку, которая и будет приближенной разверткой усеченного цилиндра.
Окружность основания и длину развертки, равную 2
R , где R – радиус цилиндра, делим
на 8 равных частей (от 0 до ). На П
2
строим проекции ребер вписанной призмы
(образующих цилиндра) и точек (1
2
…8
2
) пересечения их с секущей плоскостью
(
2
) ,
как результат пересечения проекций образующих с вырожденной проекцией плоскости
2
.
3. Через точки деления основания развертки проводим вертикальные отрезки,
равные по величине образующим цилиндра, и находим на них точки 1…8,.проводя
горизонтальные линии связи через проекции точек 1
2
…8
2
до пересечения с
соответствующей образующей.
2
=
=
=
0
2
2
=
8
5
3
4
6
2
1
=
7
22
2
2
=
2
2
6
7
8
5
4
3
2
1
8
0
=
0
=
47
3. Через точки деления основания развертки проводим вертикальные отрезки,
равные по величине образующим цилиндра, и находим на них точки 1…8,.проводя
горизонтальные линии связи через проекции точек 1
2
…8
2
до пересечения с
соответствующей образующей.
4. Построенные на развертке точки 1…8 соединяем плавной лекальной кривой. Это
будет синусоида – развертка эллипса, сечения цилиндра плоскостью
. Фигура,
ограниченная синусоидой, разверткой основания и образующими О и , является
разверткой боковой поверхности усеченного цилиндра (окрашено серым цветом).
5. Чтобы построить полную развертку усеченного цилиндра, необходимо добавить
еще НВ основания и сечения.
12.3.2.Развертка конической поверхности
Если задана поверхность прямого кругового конуса с радиусом основания R и
высотой h, то развертка его боковой поверхности представляет собой круговой сектор,
радиус которого равен длине образующей l конуса, а центральный угол
= 360
0
R/l.
Если конус усеченный, то строится его приближенная развертка – развертка
усеченной n угольной пирамиды, вписанной в конус.
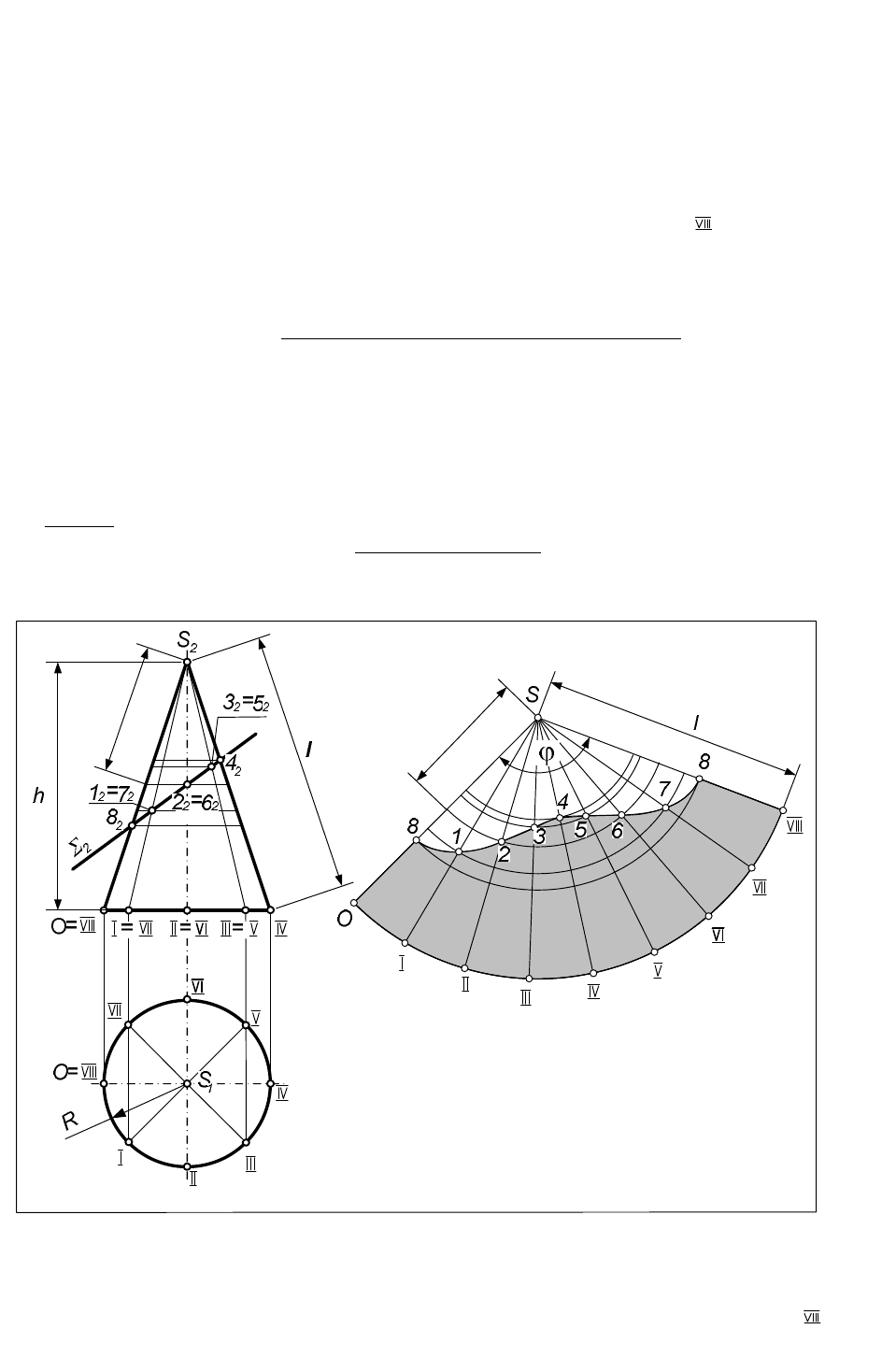
Задача. Построить развертку боковой поверхности конуса, усеченного плоскостью .
Алгоритм решения
1. Строим развертку прямого кругового конуса – круговой сектор с параметрами,
указанными выше.
Рис.69
2. Вписываем в конус правильную n угольную (на рис.69 – 8 угольную) пирамиду, для
чего делим окружность основания на 8 равных частей, находим точки деления 0 - на П
2
.и соединяем полученные точки с вершиной S.
2
,
6
r
2
,
6
r

48
3.Находим фронтальные проекции 1
2
…8
2
точек пересечения ребер плоскостью
как
результат пересечения вырожденной проекции плоскости
2
с проекциями ребер и
проводим через найденные точки проекции параллелей конуса – отрезки,
перпендикулярные оси конуса.
4. Делим на 8 равных частей дугу – развертку основания конуса и точки деления
соединяем с вершиной S на развертке.
5. Строим на развертке точки пересечения ребер вписанной пирамиды с плоскостью
как результат пересечения ребер с соответствующими проекциями параллелей на
развертке. Параллели конуса развертываются в дуги, концентричные развертке основания,
радиусы которых равны замеренному по очерковой образующей конуса расстоянию
между фронтальной проекцией параллели и вершиной S
2
. Например, параллель, на
которой расположены точки 2 и 6, разворачивается на развертке в дугу с центром в точке
S и радиусом r
2,6
.
6. Построенные на развертке точки 1…8 соединяем плавной лекальной кривой.
Фигура, ограниченная этой кривой, разверткой основания и участками ребер 0 и и
будет разверткой боковой поверхности конуса, усеченного плоскостью
. Чтобы
построить полную развертку усеченного конуса, необходимо добавить еще НВ основания
и сечения.

49
ЛИТЕРАТУРА
1. Четверухин Н.Ф. Начертательная геометрия / В.С.Левицкий, З.И.Прянишникова,
А.М.Тевлин, Г.И.Федотов.- М.: Высшая школа, 1963.- 420 с.
2. Фролов С.А. Начертательная геометрия / С.А.Фролов.-М.: Машиностроение, 1983.
240 с.
3. Рабочая тетрадь по начертательной геометрии.- Мариуполь, 2004.-46 с.
4. Методические указания по начертательной геометрии и черчению для студентов
заочной формы обучения.- Мариуполь, 2004.- 49 с.
5. Конспект лекций по начертательной геометрии для студентов машиностроительных
специальностей – Мариуполь, 2008. – 58 с.
