Adlard E.R. (ed.) Chromatography in the Petroleum Industry

Подождите немного. Документ загружается.

Chapter

autosampler, generate data and print out

report. The computer can also use es-

tablished correlations to calculate various important parameters such as car-

starting index and vapour-lock index from the GCD data.

The development of GC distillation up to

1978

was very well reviewed by

Butler

[3].

Since that time, essentially four methods for simulated distillation of

crude oils and petroleum fractions have become available, and these are now

considered

turn.

2.2

MIDDLE DISTILLATES

AM)

LUBE OILS

Simulated distillation of these fractions is covered by

ASTM

D2887,

the

scope of which requires that their boiling ranges must be greater than 55"C, and

their

final

boiling points must be less than

538°C

measured by the method.

This is the simplest

the various GCD methods because it assumes

100%

re-

covery

the sample and response factors are not used. Either flame ionization

or thermal conductivity detectors are allowed, and a wide variety of stationary

phases and column lengths may be used. The method relies for control only on a

test for column resolution determined

solution of hexadecane and octa-

decane

n-octane. Unlike the gasoline

GCD

method,

ASTM

D3710,

there are

tests for sensitivity, noise, drift, skewing of peaks,

polarity.

2.2.1

Precision

The relative simplicity of the method does not mean that it is easy to obtain

results with a high level

precision, which is what the recipients of the data

usually want. The precision data

ASTM

D2887,

given in Table

2.1,

has been

widely disbelieved for many years as too optimistic, and in fact the latest version

(

1989)

notes that the data were not obtained in accordance with

ASTM

practices.

TABLE

2.1

ASTM

D2887

PRECISION

Recovered

Repeatability Reproducibility

("C,

("C)

IBP

10-40

40-90

FBP

5.5

13.5

Advances in simulated distillation

Most laboratories practising

distillation have found it difficult to achieve

these levels of precision, especially the reproducibility figures. This is probably

a reason for

GCD

not replacing physical distillation methods such as

D2892

and

D86

in product specifications.

The most difficult points at which

achieve high precision are of course the

0-5%

and

95-100%

points. Sadly for the analyst, these are often the points of

most interest to customers. For example, the

95-100%

points of a middle distil-

late can often be correlated with wax appearance temperature, and

0-5%

of lube

oils can be correlated with oil consumption in engines. In consequence, refinery

pipestill operators monitor these points closely. Large sums of money may be

involved in achieving the optimum cut-points.

In view of the importance of precision, it is odd that there has been little pub-

lished work on ways of improving it. In the early

1980s,

an Institute

Petro-

leum sub-panel

[4]

tried closely specifjring column, flow rates and temperature

programs, but failed to significantly improve precision. In

1983,

Abbott

[5]

re-

ported that the poor precision was due, at least in part, to the lack of a common

method for calculating results from the raw data. Schwartz

al.

[6]

in a paper

comparing simulated distillation by

with SFC, made the same observation.

ASTM

D2887

gives little guidance on the calculation, which is far from straight-

forward. It suggests that area summation be started at the beginning of the run

(or after a solvent exclusion gate), and consequently a lot of noise can be accu-

mulated if the sample does not start to elute quickly. There is no algorithm to

calculate the start of the sample. It suggests that the end of the sample be taken

as the point where the signal has reached a constant low value no greater than

0.01%

of the total area counts. However, this will be dependent on the slice

width, which is not specified in the method, and therefore different computer

programs may choose the end points in different places.

A second major problem is baseline drift.

D2887

states that subtraction

baseline blank from sample runs is probably more accurate than the traditional

approach of using matched columns and detectors. However, Abbott

[5]

showed

that baselines are not constant from one run

another, nor are they related to

each other by any simple transformation. Selucky

al.

[7],

in a paper on simu-

lated distillation of coal liquids, proposed a novel baseline correction procedure

which used baseline information from the actual experimental run before and

after sample elution. They showed that this approach gave better results than the

baseline subtraction method.

Abbott suggested a calculation procedure which addressed the problems of

sample detection and baseline drift simultaneously. Baseline drift could be com-

pensated for by either matched columns or by blank subtraction, but a limit was

put on the amount allowable. The procedure also made the use of a certified ref-

erence sample mandatory. This was to be used to determine a sensitivity factor

References

pp.

52-53

Chapter

for the GCkomputer system, which was then used for subsequent samples.

small scale cooperative study showed that the procedure greatly improved repro-

ducibility, especially the

0-5%

and

95-100%

points.

Most analysts performing simulated distillations naturally

use

commercially

available programs to do the calculations, and the authors

these programs

have interpreted the existing method in various ways. Fortunately, at the time of

writing

(1992),

an ASTM task force is developing a calculation procedure for

inclusion

a future version of

D2887.

2.2.2

Capillary

columns

ASTM

D2887

allows the use of any column which meets its resolution crite-

rion and which elutes typical hydrocarbons in boiling point order. However, the

examples

gives are all with packed columns. Over the last

years or

the

use of capillary columns with internal diameters of circa

0.5

mm (wide-bore or

mega-bore) has become widespread

[8-171.

These columns can be used with

conventional injection systems and flow controllers, and have the advantage that

they usually produce little baseline drift.

This facilitates single column operation with baseline subtraction,

major

advantage

these columns

that it is often possible to elute much higher boil-

ing compounds than with packed columns. Of course, this means that they

beyond the scope of

D2887,

which is limited to a final boiling point of

538OC,

and they will be discussed

more detail in Section

2.2.3

Aromatics

and

heteroatoms

well known that not all hydrocarbons elute from non-polar columns in

boiling point order, and that compounds incorporating heteroatoms have differ-

ent detector response factors from hydrocarbons.

D2887

addresses these prob-

lems

an appendix to the method. It shows that the deviation of simulated dis-

tillation boiling points from actual boiling points for

compounds, including

polycyclic aromatics and heterocyclics, does not introduce any significant error

when compared

physical distillation. A comparison of true boiling point data

(obtained

high efficiency spinning band cohmn) and simulated distillation

data

for

virgin gas oil, a high sulfur gas oil, and a highly aromatic

gas

oil

showed reasonable agreement. It is significant that the agreement was with

weight

TBP data.

the early development of simulated distillation methods,

reviewed by Butler

[3],

there was disagreement about whether

GCD

correlated

with weight

or volume

TBP

methods. The conclusion

the

D2887

ap-

pendix was supported

Kiser and Malone

[IS],

working with coal liquids.

7'11t.y

noted that none

the polycyclic aromatics mentioned in the ASTM

Advances in simulated distillation

D2887 appendix had alkyl substituents, whereas real samples do. They under-

took a rigorous comparison of simulated distillation with direct TBP distillation

and also with TBP data computed from ASTM D86 data. They found good

agreement with weight

TBP data, and also noted that the repeatability of GCD

was better than that of the TBP data. Similarly, Pannell and Sood [19], also

working with coal liquids, found that there was a maximum

difference in the

cumulative weight

at any boiling point between GCD data and TBP data.

another paper on coal liquids, Selucky [7] suggested that since the “para-

ffinic scale” and “aromatic scale” were the two extremes, a calibration curve

adjusted for aromaticity (e.g. from

NMR

measurement) would improve results.

Petroff

al.

[20] reported that differences between calibration with n-paraffins

and aromatics could be avoided by the use of Dexsil

300

as stationary phase in-

stead of the more widely used non-polar silicone fluids. This was especially true

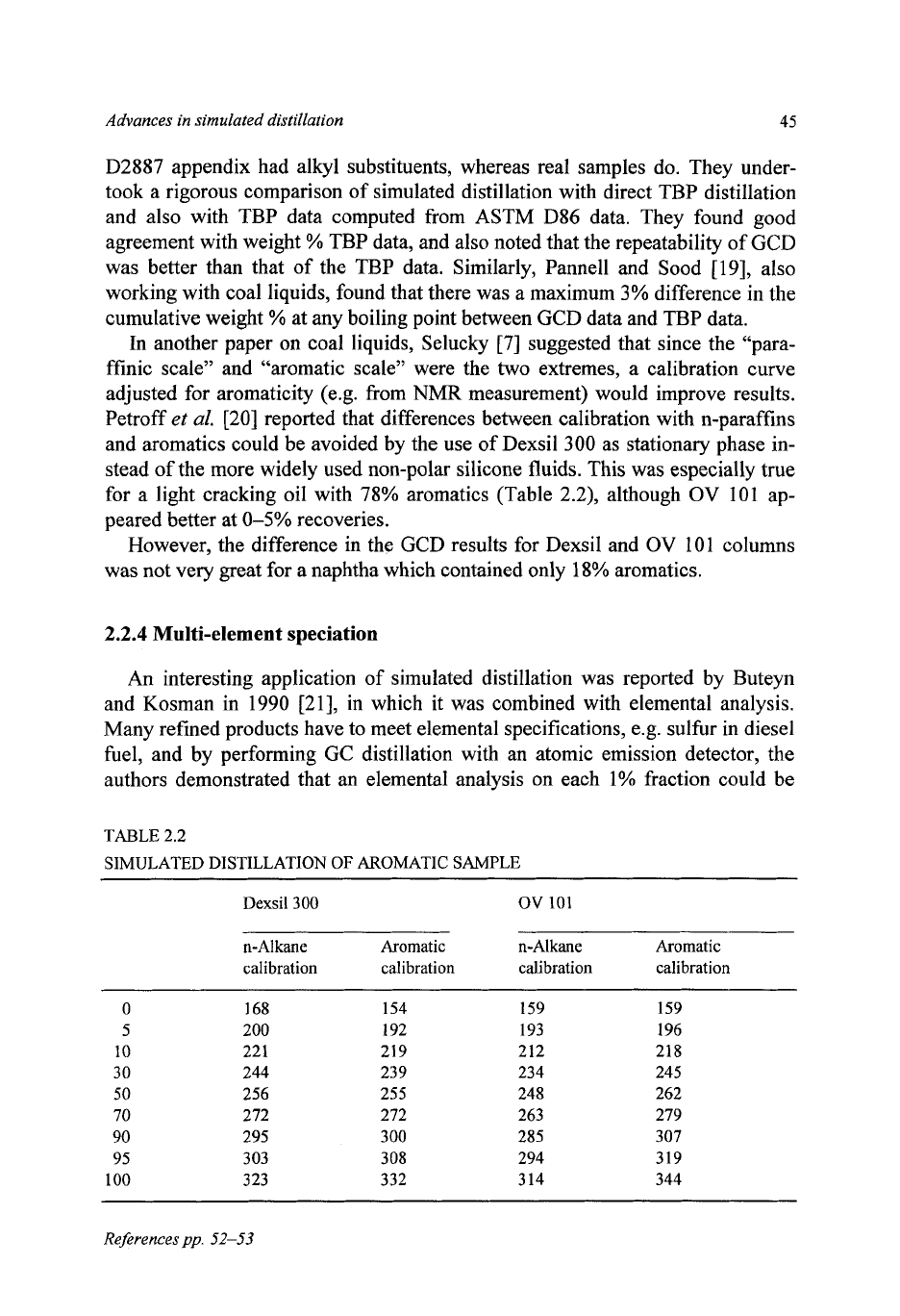
for a light cracking oil with 78% aromatics (Table

2.2),

although

101 ap-

peared better at

0-5%

recoveries.

However, the difference in the GCD results for Dexsil and

101

columns

was not very great for

naphtha which contained only

18%

aromatics.

2.2.4

Multi-element speciation

An interesting application of simulated distillation was reported by Buteyn

and Kosman in 1990 [21], in which it was combined with elemental analysis.

Many refined products have to meet elemental specifications, e.g. sulfur in diesel

fuel, and by performing GC distillation with an atomic emission detector, the

authors demonstrated that an elemental analysis on each

fraction could be

TABLE 2.2

SIMULATED DISTILLATION

AROMATIC SAMPLE

101

n-A1

kane Aromatic

n-Alkane

Aromatic

calibration calibration

100

168

200

221

244

256

272

295

303

154

192

219

239

255

272

300

308

332

159

193

212

234

248

263

285

294

3 14

159

196

218

245

262

279

307

319

344

References

pp.

52-53

Chapter

achieved. Further information on this is given in Chapter

on the atomic emis-

sion detector.

2.3

GASOLINES AND GASOLINE FRACTIONS

The ASTM method for gasolines,

D37

10,

is much more complex than that

for

middle distillates and lube oils which has just been discussed. This is primarily

because individual hydrocarbons in the gasoline boiling range have quite differ-

ent response factors in either flame ionization

thermal conductivity detectors.

The scope of the method limits the final boiling point to

260°C,

and response

factors are determined from

standard such that the results are given in volume

whichever detector is used. Conditions are selected such that iso-pentane and

lighter saturates are measured individually, and heavier compounds are measured

pseudo-components of narrow boiling range. The calibration mixture for this

method is a complex one of pure compounds covering the boiling range.

used not only

for

the conversion of retention time to boiling point, but also for

response factors which are applied to individual compounds and to the pseudo-

components.

is also used for system performance checks such as resolution,

sensitivity, noise, drift and peak skewness.

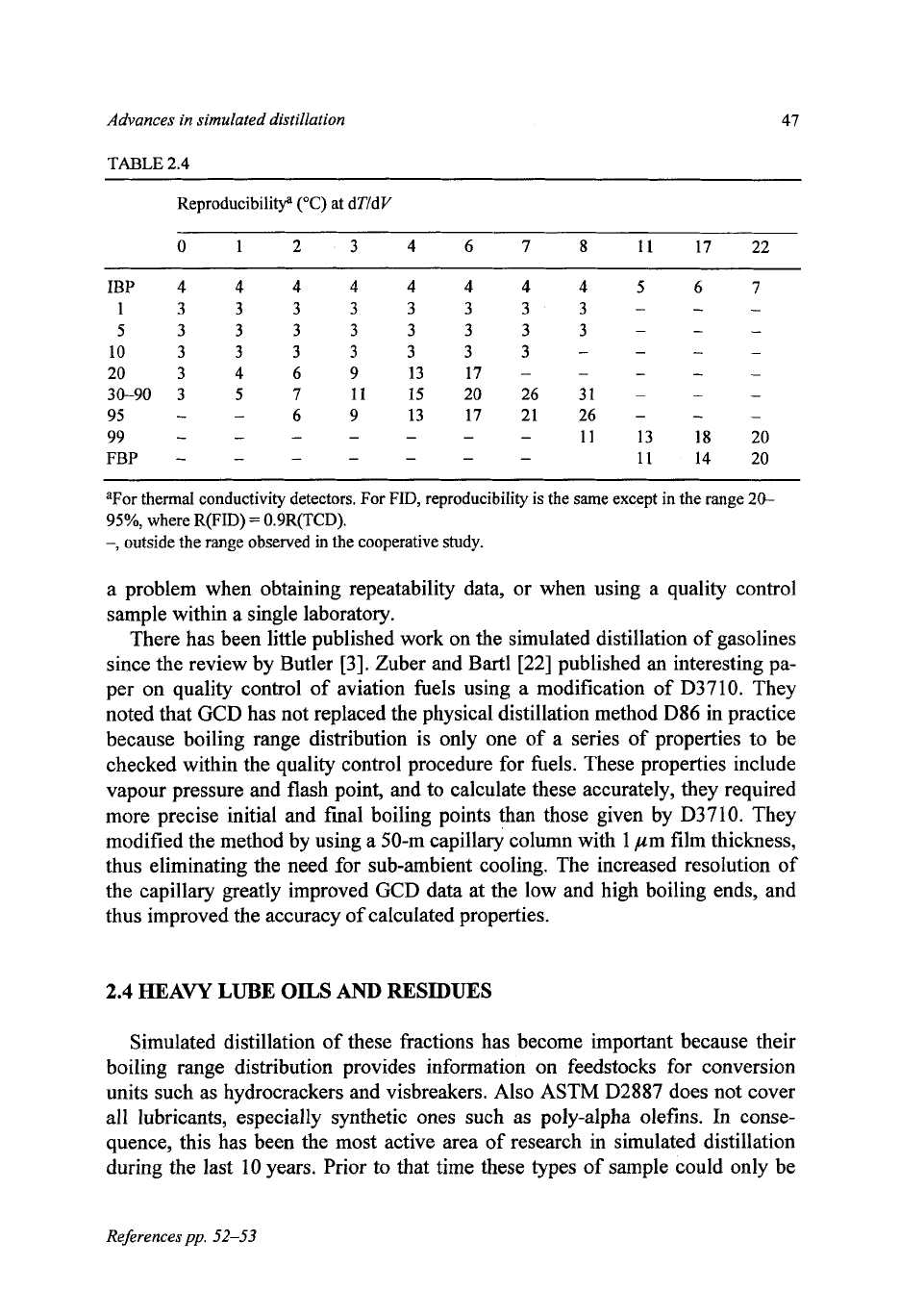
The precision of the method depends on the shape

the boiling range distri-

bution curve. Both repeatability and reproducibility vary with the rate of change

temperature with percent recovered. The precision data are given as Tables

2.3

and

2.4.

It is worth noting that a significant problem with gasoline samples is

sample integrity. Gasolines contain high volumes of very low boiling compo-

nents which are easily evaporated if stringent precautions are not taken. This is

major problem in cooperative testing to obtain reproducibility data, and it can be

TABLE

2.3

Repeatability

("C)

dTldV

1 1 1

1 1

- -

33 3

3 3 3

- -

- - -

- -

Advances in simulated distillation

TABLE

2.4

Reproducibilitya

(“C)

at dT/dV

17 22

IBP

4 4

3 3 3 3 3

3 3 3 3

3 3 3

3 3 3 3 3

30-90

20 26

- -

21 26

FBP

- -

14 20

- -

aFor

thermal conductivity detectors.

For FID,

reproducibility

the same except in the range 20-

95%,

where

R(FID)

0.9R(TCD).

outside the range observed in the cooperative

study.

a problem when obtaining repeatability data, or when using a quality control

sample within a single laboratory.

There has been little published work on the simulated distillation

gasolines

since the review by Butler

[3].

Zuber and Bart1 [22] published

interesting pa-

per on quality control

aviation fuels using a modification

D3710.

They

noted that

GCD

has not replaced the physical distillation method

D86

in practice

because boiling range distribution is only one

a series of properties to be

checked within the quality control procedure for fuels. These properties include

vapour pressure and flash point, and to calculate these accurately, they required

more precise initial and final boiling points than those given by

D3710.

They

modified the method by using a 50-m capillary column with

pm film thickness,

thus eliminating the need for sub-ambient cooling. The increased resohtion

the capillary greatly improved

GCD

data at the low and high boiling ends, and

thus improved the accuracy of calculated properties.

2.4

HEAVY

LUBE OILS

AND

RESIDUES

Simulated distillation

these fractions has become important because their

boiling range distribution provides information on feedstocks for conversion

units such as hydrocrackers and visbreakers. Also ASTM

D2887

does not cover

all lubricants, especially synthetic ones such as poly-alpha olefins.

conse-

quence, this has been the most active area

research in simulated distillation

during the last

years. Prior to that time these types of sample could only be

References

pp.

52-53

Chapter

subjected to

GCD

by using an internal standard procedure with either backflush

of the whole column or, preferably, a pre-column. However,

proposed

ASTM

method using this approach was never advanced to method status because

lack of adequate precision.

Assigning boiling points to alkanes higher than

C60

is a problem because they

cannot be distilled even under vacuum. They are obtained by extrapolation of the

curve correlating n-alkane boiling points with carbon number

[23].

Some authors

emphasise the "unreal" nature

the values [24].However, the people who use

the data, such as pipestill operators and lubricants formulators, rarely question

the results since they are usually interested in comparative values.

1985.

Luke and Ray [S] published their paper on

GCD

of atmospheric resi-

dues using short

m) pyrex capillary columns with only

0.15

film

thickness

of the silicone stationary phase

OV-1.

They used a stainless steel capillary re-

strictor

that the hydrogen carrier gas could be flow controlled, and they used

cold on-column in-jection to avoid discrimination. The column was programmed

from

390°C

and it was shown that residues boiling up to

650°C

(carbon

number

70)

could be analysed by this technique.

The paper by Luke and Ray was closely followed by one from Trestianu

al.

191,

which described a dedicated system for

GCD

of heavy petroleum fractions.

The system utilized pressure and flow control for the carrier gas and an auto-

matic on-column injector. They demonstrated the elution of n-alkanes up to

Cl20

within the temperature program, which went to 43OoC, and up to C140

during the final isothermal hold. Repeatability of the dedicated system was

shown to be very good, and the lower part of the distillation curves fitted very

well with those obtained by D2887.

Other authors also reported

GCD

of heavy fractions using capillaries

[

10-1

71,

and Firor

[

151

showed that fused silica capillaries could be prepared for use up

400"C,

thus obviating the need for aluminium-coated silica

glass columns.

Recently, metal capillary columns with the stationary phase chemically bonded

to the internal surface have been introduced [25].

There are alternatives to high temperature

for the simulated distillation of

high boiling fractions, such as supercritical fluid chromatography (SFC) and

vacuum therinogravimetry

(TGA).

concern with high temperature

GCD

de-

scribed earlier

that petroleum fractions

are

known to decompose at tempera-

tures above about 3

50°C.

Decomposition depends not only

temperature but

also

on sample composition and residence time at high temperature.

SFC

has

enjoyed a resurgence of interest in recent years, and Schwartz

al.

[26] reported

its

first application to sitnulated distillation. They used a 10-m 50pm internal

diameter capillary column coated with a non-polar stationary phase. The column

had an integral restrictor which gave

3.4

ml/min

flow

when used at

1800

psi of

liquid carbon dioxide and at room temperature. An

HPLC

valve was used as the

Advances in simulated distillation

injection system, which was connected to the column by means of a simple

splitter. At an oven temperature of 100°C and using a linear pressure program of

2000-5500 psi of carbon dioxide, they found that C80 eluted in around 21 min,

and that retention time repeatability of the n-paraffin calibration standard was

excellent. The method was applied to an atmospheric residuum with a boiling

range of 345-770°C.

In a later paper, Schwartz

al.

[6]

gave a more detailed account of simulated

distillation by capillary SFC. They also compared the technique

GCD and to

simulated distillation by TGA. In fact, they used TGA with and without vacuum

to show that an Arabian heavy crude residue started to decompose thermally at

around 370°C and reached a maximum at 430°C. Decomposition products were

confirmed by using TGA linked on-line to a GUMS system. The capillary SFC

conditions which they studied included column type, fluid density and tempera-

ture, and discrimination effects in the inlet splitter. This last factor is important

because, while the sample may be soluble in a solvent prior to injection, precipi-

tation may occur just after injection when the sample is exposed to carbon diox-

ide at relatively low density. They concluded that an oven operating temperature

100°C overcame this problem. The pressure program was optimized

that

samples with a boiling range of 120-760°C could be analysed. Three lubricating

oils were then analysed by GCD (ASTM D2887) and by capillary SFC, and a

regression analysis indicated no systematic difference between the two sets of

results. The authors also compared SFC with a vacuum TGA method of simu-

lated distillation described in detail in the paper. Two sets

atmospheric resi-

dues were cut into five fractions using short path distillation at high vacuum, and

each fraction was analysed by both methods. Regression analysis of the data

showed that SFC gave higher values than VTGA at low boiling points while the

reverse was true at higher boiling points. The authors considered that this might

have been caused by the calibration method used for VTGA, which was non-

linear in the upper temperature region.

Schwartz published a further paper on simulated distillation by SFC in 1988

[27], this time using packed columns. The advantages of these were said to be

high loadability (i.e. no splitter), good quantitation, and faster analysis time. A

10-cm column packed with 7pm polysiloxane

allowed elution of ClOO in

about 20 min. A comparison of packed SFC, capillary SFC and VTGA showed

good agreement. An important advantage of packed SFC was its ability to accept

undiluted samples such as crudes, and this is discussed in Section 5.

As noted by Thomson and Rynaski [28], simulated distillation by SFC has not

been widely adopted as problems have been encountered with the injection of

high boiling samples. However, they show that much improved sample introduc-

tion techniques are now available, and in their analysis of wax samples they

found that SFC and high temperature GC gave equally good results.

References

pp.

52-53

Chapter

Other approaches to simulated distillation of heavy fractions have

also

been

reported. Petroff

al.

[20],

in their wide-ranging paper on the application of

GCD

to petroleum product control, described the use of temperature pro-

grammed injection and the backflush of a pre-column. They used an internal

standard

C14416

to calculate sample recovery. DiSanzo

al.

[29]

used

very similar procedure and reported excellent long-term precision

for

lubricat-

ing oil with boiling range

390-590°C.

Abbott

[30]

described a valveless method

of backflushing which used flow controllers rather than the pressure controllers

used in a Deans system

[31].

The advantage was that a wide temperature pro-

gram could be used, such as for heavy residues. Finally,

Curvers

and van den

Engel

[24]

described commercially available equipment incorporating

tempera-

ture programmed injector and a wide-bore high temperature column.

2.5

CRUDE

OILS

Crude oils pose all the problems of the previous three sections for simulated

distillation: precision, variable response factors, non-recoverable residues, etc.,

and a viable method for crudes has been a goal

for

chromatographers since the

early days of the technique. As mentioned in the Introduction, TBP data

for

cru-

des can be obtained by ASTM D2892, but the method can take days to complete.

TBP

data

crudes is very valuable to logistics planners and pipestill operators,

a simulated distillation method taking only

h would be an extremely attrac-

tive proposition.

The ASTM published a proposed method in 1976, which involved analysing

the sample with and without the addition of an internal standard of

C14

C17 n-

paraffins. This allowed calculation of sample recovery, typically up to

538°C.

The method was never advanced to standard status because of inadequate preci-

sion obtained

cooperative testing programmes. Even

so,

the method is used,

and Maynard and Michalik

[32]

report that the use of robotics to prepare the

samples has greatly improved precision. Analysis of

Mexican crude with boil-

ing

range 200-450"C and

22%

residue gave a standard deviation of 1.1% for the

residue and 2.3"C throughout the boiling range.

Petroff

al.

[20] used a more sophisticated version of the proposed ASTM

method. Their equipment incorporated a programmable temperature vaporizer

and a pre-column which was backflushed to prevent heavy residues from con-

taminating the analytical column. They found good agreement between

GCD

and

D2892

results for Kuwait and Boscan crudes.

Schwartz

[27]

used packed column

SFC

for simulated distillation

Maljamar

crude.

order to minimize the sample volume placed on the column, a fast

valve injection time was used. He was able to show the separation of early

Advances in simulated distillation

eluting sample components, and presumably the technique was able to go up to

C 100 as before (Section 4), but unfortunately the paper did not include precision

data.

Coulombe and Duquette, in a paper on SFC of crude fractions [33], noted that

response factors for sulfur and nitrogen containing compounds can be quite dif-

ferent from hydrocarbons. This appears to be an area which has received insuf-

ficient attention, since crude oils vary greatly in their content of heteroatoms.

2.6

PROCESS CONTROL

AND

OTHER APPLICATIONS

Simulated distillation is probably used to control processes in hundreds of

lo-

cations around the world, but mostly off-line. However, as long ago as 1975 Bird

and Kimball described the application of on-line gasoline GCD to refinery proc-

ess control and blending operations. A significant advance since the review by

Butler [3)]has been the introduction of simulated distillation by on-line SFC,

reported by Levy [34]. As described in Section

SFC extends the boiling range

which can be analysed to as high as 800°C, and thus simulated distillation data

can now be obtained on-line for refinery units processing heavy residues. The

system incorporates a supercritical fluid extraction cell, which is necessary be-

cause of the viscous nature of the samples. It also means that the sample is in-

jected as a dilute solution in carbon dioxide, thus avoiding many of the injection

problems found in SFC, and it ensures that the capillary column is not over-

loaded.

In a related application, Abbott reported that GCD data could be used for the

automatic identification of leakages in refineries [35]. Traditionally, unknown

samples in refinery sewer systems have been identified by comparing them with

a library of “fingerprints”, preferably obtained by capillary GC. This approach

uses only the areas or heights of easily recognised peaks, and it requires an ex-

perienced operator to interpret the results. GCD data is in effect a way of digitiz-

ing a chromatographic trace, and Abbott combined it with peak area data to pro-

duce a system in which unknown samples were identified by a computer pro-

gram. Obviously many of the leakage samples are weathered, but this problem is

solved by including data from artificially weathered products in the computer

database.

GC distillation can be used to determine gasoline fuel dilution of used engine

oils, although there is a separate ASTM method (D3525) for this purpose. How-

ever, GCD cannot be used for diesel fuel dilution of engine oils because of the

substantial overlap of fuel and lube. Fuels have a typical boiling range of C8-

C26 and lubes from C18440. Adlard and Davies overcame this problem by us-

ing a GCD type of analysis, in that the chromatogram was acquired as area time

References

pp.

52-53