Accardi L., Freudenberg W., Obya M. (Eds.) Quantum Bio-informatics IV: From Quantum Information to Bio-informatics
Подождите немного. Документ загружается.


50
Theorem
3.5.
Let
H
be
a bounded self-adjoint operator with Hypothesis
(H). Then there exist no
time
operators T
of
H such that
:Fa
C
D(T),
Ran(T)
c:F
and:F_
is a
CCR-domain
for (T,
H).
Acknowledgments
The
author
would like
to
thank
Professor M.
Ohya
for
inviting
him
to
present
a
lecture
at
the
International
Conference
QBIC'lO
(Noda
Campus
of
TUS,
March
10-13, 2010).
This
work was
supported
by
the
Grant-In-Aid
No.21540206 for Scientific
Research
from
Japan
Society for
the
Promotion
of
Science
(JSPS).
References
1.
A.
Arai,
Generalized
weak
Weyl
relation
and
decay
of
quantum
dynamics,
Rev. Math. Phys.
17
(2005) ,
1071-1109
.
2. A.
Arai,
Spectrum
of
time
operators,
Lett. Math. Phys.
80
(2007), 211-221.
3. A.
Arai,
Some
aspects
of
time
operators,
in
Quantum Bio-Informatics (Edi-
tors: L.
Accardi,
W.
Freudenberg
and
M.
Ohya),
World
Scientific,
Singapore,
2008,
26-35.
4.
A.
Arai,
On
the
uniqueness
of
weak
Weyl
representations
of
the
canonical
commutation
relation,
Lett. Math. Phys.
85
(2008),
15-25.
5.
A.
Arai,
Necessary
and
sufficient
conditions
for a
Hamiltonian
with
discrete
eigenvalues
to
have
time
operators,
Lett. Math. Phys.
87
(2009),
67-80.
6. A.
Arai
and
Y.
Matsuzawa,
Construction
of
a
Weyl
representation
from a
weak
Weyl
representation
of
the
canonical
commutation
relation,
Lett. Math.
Phys.
83
(2008),201-211.
7.
A.
Arai
and
Y.
Matsuzawa,
Time
operators
of
a
Hamiltonian
with
purely
discrete
spectrum,
Rev. Math. Phys.
20
(2008), 951-978.
8.
R.
Caballar
and
E. A.
Galapon,
Characterizing
multiple
solutions
of
the
time-
energy-canonical
commutation
relation
via
quantum
dynamics,
Phys. Let. A
373
(2009), 2660-2666.
9. G.
Dorfmeister
and
J.
Dorfmeister,
Classification
of
certain
pairs
of
operators
(P,
Q)
satisfying
[P,
QJ
=
-iId,
J.
Funct. Anal.
57
(1984),
301-328.
10. E. A.
Galapon,
Self-adjoint
time
operator
is
the
rule for
discrete
semi-
bounded
Hamiltonians,
Proc. R. Soc. Lond. A
458
(2002),2671-2689.
11. M.
Miyamoto,
A
generalized
Weyl
relation
approach
to
the
time
operator
and
its
connection
to
the
survival
probability,
J.
Math. Phys.
42
(2001),
1038-1052.
104,
570-578.
12. K.
Schmudgen,
On
the
Heisenberg
commutation
relation.
I, J. Funct. Anal.
50
(1983),
8-49.
13.
K.
Schmudgen,
On
the
Heisenberg
commutation
relation.
II, Publ.
RIMS,
Kyoto Univ.
19
(1983),601-671.

Quantum
Bio-Informatics
IV
eds. L.
Accardi,
W.
Freudenberg
and
M.
Ohya
© 2011
World
Scientific
Publishing
Co.
(pp
.
51
- 60)
QUANTUM
UNCERTAINTY
AND
DECISION-MAKING
IN
GAME
THEORY
M.
ASANO,
M.
OHYA
and
Y.
TANAKA
Department
of
Information
Sciences,
Faculty
of
Science
and
Technology,
Tokyo
University
of
Science,
Noda
City, Chiba 278,
Japan
A.
KHRENNIKOV
and
1.
BASIEVA
International
Center
for
Mathematical
Modelling
in
Physics
and
Cognitive
Sciences
Linnaeus
University,
Viixjo,
S-35195
Sweden
Recently
a few
authors
point
ed
to
a
possibility
to
apply
the
mathematical
formal-
ism
of
quantum
mechanics
to
cognitive
psychology,
in
particular,
to
games
of
the
Prisoners
Dilemma
(PD)
type.
6
_
18
In
this
paper,
we
discuss
the
problem
of
ratio-
nality
in
game
theory
and
point
out
that
the
quantum
uncertainty
is
similar
to
the
uncertainty
of
knowledge
,
which
a
player
feels
subjectively
in
his
decision-making.
1.
Introduction
Game
theory
is
an
applied
mathematics
used in
the
various disciplines;
the
social sciences, economics, political science,
international
relations, com-
puter
science,
and
philosophy.
This
theory
analyzes
an
interdependency
of
decision-making
entities
(players)
under
a
certain
institutional
condi-
tion.
In
a
normal
form
of
game, players have some
strategies
to
be
chosen
and
obtain
payoffs which are assigned for results
of
their
choices.
About
the
player's decision-making,
the
following
three
assumptions
are
required:
First,
it
is
assumed
that
players know
the
rule of game; each player knows
all selectable
strategies
and
payoffs. Second,
it
is
assumed
that
a player
behaves
rationally
so as
to
maximize his own payoff.
Third,
it
is
assumed
that
each
rational
player recognizes
rationalities
of
other
players. Generally,
the
rationality
contains
the
faculty
of
reasoning,
and
the
second assump-
tion
and
the
third
one
can
not
be
discussed distinctively. A
rational
player
makes a decision by his
rationality
and
reasoning
rational
behaviors
of
other
players.
A goal of
game
theory
is
to
explain various interdependencies in
the
real
world,
and
it
is believed
that
the
concept of Nash equilibrium provides a
51

52
normative
solution
for such
explanation.
However,
there
are
some experi-
ments
of
games
with
Nash
equilibriums, in which,
real
players frequently do
not
achieve
the
Nash
equilibrium,
and
it
seems
to
be
irrational.
1_5
About
this
fact, someone
may
think
it
is a
matter
of
course
that
there
are
some
players
who
make
decisions roughly,
and
someone
may
think
players edu-
cated
about
game
theory
should
not
make
such
a mistake.
These
opinions
might
be
reasonable
in
some
cases, however, we believe
that
there
are
cases
that
a real
player's
decision-making process is essentially different from a
normative
player's
one
in
conventional
game
theory. We discuss
this
point
by
using several
examples
of
games.
Firstly
we consider
the
following game.
A/B
DE
IE
DA
4/4
2/5
IA
5/2
3/3
This
is a well-known two-player
game
called a
prisoner's
dilemma
(PD)
game.
The
players A
and
B have two
strategies
denoted
by
DA,E
and
IA,E,
and
the
values
of
payoffs
are
assigned for
results
of
(DA'
DE),
(DA'
IE),
(lA,
DE)
and
(lA,
IE)'
Generally,
PD
game
has
a
unique
Nash
equilibrium:
Since
the
dominant
strategies
IA
and
IE
are
best
for
the
rational
players
A
and
B,
the
result
(lA,
IE)
is
the
solution
of
Nash
equilibrium. A
player's
decision-making process is
described
as
a
combination
of
the
player's
ra-
tionality
and
the
reasoning
about
the
another
player's
rationality.
The
diagram
in Fig. I shows
the
player
A's
decision-making process.
(DA,Ds)
••••••••••••••
(DA,
1 s)
(1A,Ds)
•..•••••••••••
~
(1A,1s)
Figure
1.
Player
A's
preference
............
Player
S's
preference
reasoned
by
A
53
The
two solid arrows in
this
diagram
explains
that
the
player A
pr
efers
the
result
(l
A
,OB)
to
(OA,OB)
and
prefers
(lA,lB)
to
(OA,l
B
).
The
two
dotted
arrows explains
that
the
player A reasons
that
the
player B will
prefer
(OA,
1B)
to
(OA,
OB)
and
prefers
the
result
(lA,
1B)
to
(lA,
OB).
These
arrows represent flows
of
the
A's
thinking.
One
can
see
that
the
A's
thinking
always reach
the
expectation
for
the
result
(lA,l
B
),
namely,
the
player
A chooses
1A
with
believing
the
player B will choose
lB.
However,
we
wonder
whether
such
the
description
of
decision-making process is enough
to
explain a real player's
thinking
or
not. Let us consider
the
case
of
the
following prisoner's
dilemma
game;
A/B
OB
1B
OA
100000/100000
2/100000
+ 1
1A
100000 +
1/2
3/3
If
an
experiment
of
this
game
is given, we
expect
many
real players will
choose
the
strategy
0,
and
their
decision-making is similar
to
th
e following
player
A's
one:
The
player A which we assume, feels strongly
that
the
payoff 100000
at
the
res
ult
(OA,OB) is very
attractive,
compared
with
the
payoff 3
at
(lA,
1B)' Moreover, he reasons
"another
player B will
think the
same
thing.
11
Both
players prefer
the
result
(OA,
OB)
to
(lA,
1B)'
The
player
A
cannot
neglect
this
fact
in
his decision-making,
and
there
is a possibility
to
shift his
expectation
from
(1
A,
1
B)
to
(0 A, 0 B), as seen in
the
diagram
of
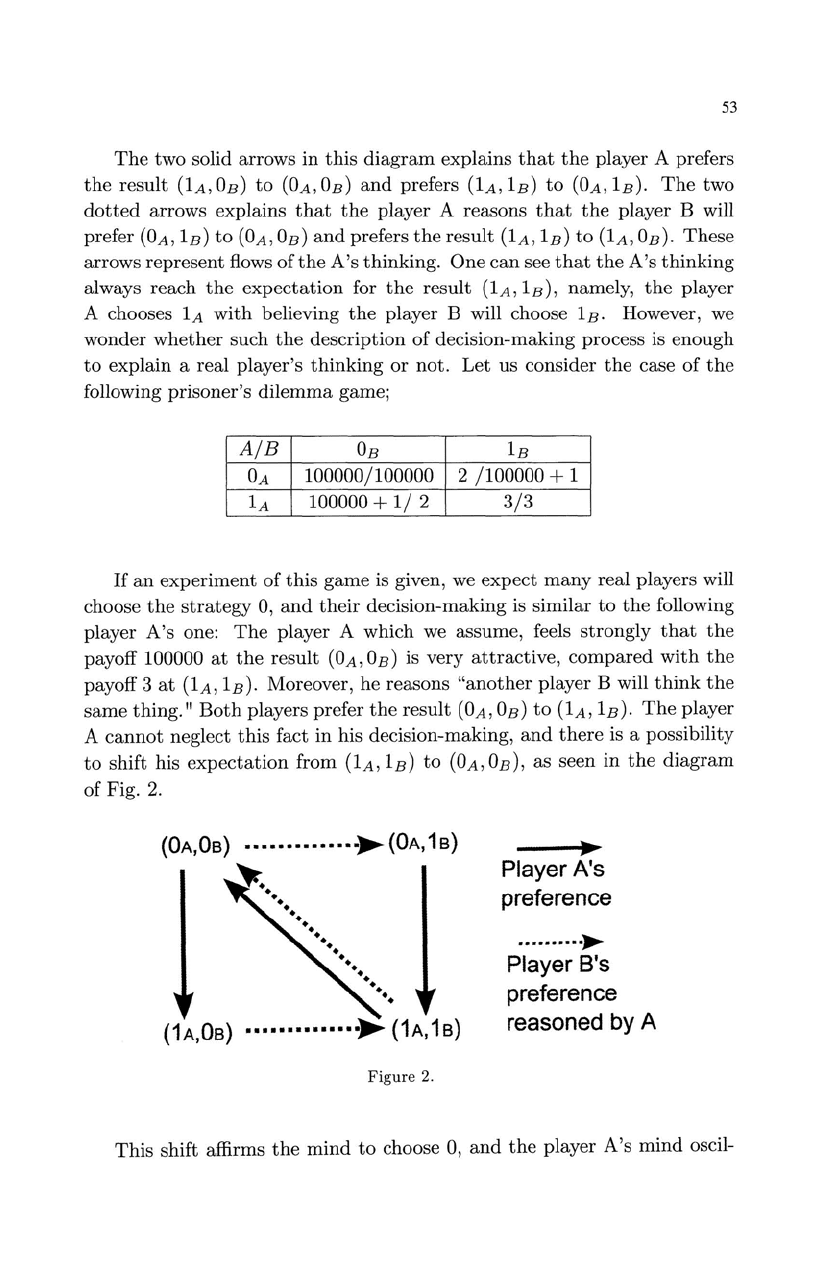
Fig. 2.
(OA,OB)
••••.••••.••••
~(OA,1B)
(1
A,
OB)
...............
(1
A,
1
B)
Figure
2.
Player
A's
preference
..........
~
Player
B's
preference
reasoned
by
A
This
shift affirms
the
mind
to
choose
0,
and
the
player
A's
mind
oscil-

54
lates between
the
choice of
1A
and
the
choice
of
OA.
Here,
note
that
the
mind
to
choose
1A
works for increasing a player's payoff by only
1.
On
the
other
hand,
the
mind
to
choose
OA
works for increasing
the
payoff by
100000 -
3.
It
is clear
that
the
mind
to
choose
OA
is
dominant.
Such
the
additiona
l effect
in
decision-making process
can
be
discussed in
various games,
but
not
on
ly
the
type
of
prisoner's dilemma. For
examp
le,
let us consider
the
game
with
the
tab
le bellow.
In
this
game,
the
result
AlB
OB
1B
OA
41 100000 + 1
100000 I 100000
1A
5 I 4 4 I 0
(lA,
OB)
is a unique Nash equilibrium. However, as seen
in
the
diagram
of
Fig. 3, by assuming
the
comparison between
the
result (lA,
OB)
and
(OA,
1B) in
the
player
A's
decision-making process, we
can
expect
that
the
player
A's
mind
will oscillate.
(OA
,
OS)
..................
(OA,1
S)
(1A,1
s)
Figure
3.
Player
A's
preference
..........
~
Player
B's
preference
reasoned
by
A
The
additiona
l shifts
in
Fig. 2
and
Fig. 3 might seem
to
be
strange
in
the
framework
of
the
game
theory. Conventionally,
the
player A's preferences
are
explained in
the
contexs as "
If
the
player B chose x B E
{O
B, 1 B },
then
I will prefer
to
choose
YA
E
{OA
, 1A}",
and
the
player
B's
preferences
reasoned by
the
A
are
explained in
the
same
form. Such a contex consists
of
two
parts
;
the
part
of
assumption
and
the
part
of
analysis.
In
the
first
part
,
the
player A assumes one
of
the
player
B's
choices.
In
the
second
part,
the
player A
ana
li
zes his preference wi
th
based
on
the
assumption.
Note
that
such
an
analysis is contextually
same
with
a posterior analysis

55
by someone
who
already
knows a
result
of
the
B's
choice.
In
principle, each
player is
not
informed
of
another
player
's choice,
and
actually,
the
player A
will
just
have
to
perform
a prior analysis.
The
conve
ntional
game
theory
gives a
prior
analysis
based
on
the
concept
of
mixed storategy,
wh
ere
the
player A
assumes
the
player B chooses
OE
or
IE
probabilistically,
and
the
A
analyzes his preference in
the
comparison
between
the
expectation
values
of
payoffs. However,
such
the
analysis
is
just
a mixture
of
the posterior
analyses
based
on
the
probabilistic
distribution
about
the
B's
choice. Such
the
prior
analysis
never
explains
the
effects
of
the
additional
shifts in Fig. 2
and
Fig. 3.
Generally, a player
who
performs
a
prior
analysis, holds uncertainty
about
another
player's
choice.
In
the
concept
of
mixed
strategy,
it
is rep-
resented
by
a simple
probabilistic
distribution.
On
the
other
hands,
the
uncertainity
we consider
can
not
be
explained
by
the
classical
probability
theory. Actually, a few
authors
pointed
to
a possibility
to
apply
the
math-
ematical
formalism
of
quantum
mechanics
to
cognitive psychology.
6_18
It
was found
that
statistical
data
obtained
in
some
experiments
of
cognitive
psychology.
The
theory
of
qunatum
physics teaches us
that
there
is a phe-
nomenon
which
cannot
be
explained
by
the
classical
probability
theory,
and
it
means
that
a
prior
analysis
about
a
phenomenon
is essentially different
from a simple
mixture
of
posterior
analyses.
We
explain
this
point
by
in-
troducing
the
example
of
the
double slit experiment.
Let
us consider
the
experimental
apparatus
shown in Fig. 4, which consists
of
the
two
plates
with
three
slits
and
the
photo-sensitive
plate.
A
photon
passing
through
the
first
and
second
plates
is
detected
on
the
photo-sensitive
plate.
If
the
slit-Ion
the
second
plate
is closed, see Fig. 5,
photons
which
are
detected
on
the
third
plate
certainly pass
through
the
slit-O.
Then,
one
can
obtain
the
distribution
of
photons
as seen in Fig. 5.
If
the
slit-O is closed, one
can
see
the
distribution
of
Fig.
6.
Next,
we consider
the
case
that
the
photon
detectors
are
placed
near
the
two
slits
on
the
second
plate.
By
these
detec-
tors, one
can
know which slit a
photon
passes
through.
The
distribution
of
photons
in
this
case
exactly
corresponds
to
the
simple
mixture
of
the
distributions
in
Fig. 5
and
Fig.
6,
see Fig.
7.
Lastly, we consider
the
case
that
the
detectors
are
removed,
and
then
,
one
can
never know which slit a
photon
passes
through.
The
distribution
of
photons
forms
an
interference
pattern,
and
it
is clearly different form
the
result
of
Fig. 7, see Fig. 8.
Here, we explains
the
mathematical
representations
of
states
of
photons
in
the
above
double
slit
experiments.
Firstly,
in
the
case
of
Fig. 5, we
denote
56
0--
photon
photo~sensitive
plate
Figur
e
4.
Double
Slit
Experiment
0--
photon
~
~
,''''
[<J
"'"
Figure
5.
I'hO!lHIen.itive plate
a
state
of
photon
passing
through
the
slit-O by
10)
=
(~)
E
<e
2
which is
called a
state
vector defined
in
the
Hilbert space 1i =
<e
2
•
Similarly, a
state
of
photon
passing
through
the
slit-l
in
Fig. 6 is
denoted
by
11)
=
(~)
E
<e
2
These
vectors
are
orthogonal each other. Also,
these
are
often represented
0 -
photon
Fig
ur
e 6.
photo-sensi
ti
ve plate
0 -
photon
~
~
ph
ot
o
.de
tect
or
s
litO
~
,
~:
~
"
11
photo-sensitive plate
Fi
g
ur
e 7.
in
the
form
of
density
operators
as
10
)
(0
1
~
m
CO)
~
(~~)
=0
PO'
11
) (
11
~
G)
(01)
~
e~)
=0
p,
57
The
density
operator
is useful for
the
statistical
description:
The
photon
such
that
passes
through
the
slit-D, 1
with
the
probabilities p
and
1 - p is

58
phut&-scn
sitive
,,13tt:
Figure
8.
represented by
In
the
case
of
Fig.
7,
the
two
photon
detectors
check
photons
that
certainly
pass
through
either
the
slit-O
or
the
silit-1.
The
state
of
photon
averaged
statistically
is
written
as
the
p
with
the
above form.
The
state
of
photon
in Fig. 8 is described
in
the
form specific
to
the
quantum
mechanics
that
is called
the
quantum superposition.
The
state
of
quantum
superposition
is
given by
the
density
operator
(
l
al2
af3*)
p = I¢) (¢I =
a*
f3
1f31
2
.
Here, I¢) is
the
state
vector defined by I¢)
==
a
10)
+
(311)
=
(~),
where
a
and
f3
are complex numbers satisfying l
al
2
+
1f31
2
=
1.
The
a
and
f3
are
called probability amplitudes,
and
the
squares of
them,
lal
2
and
1f31
2
,
have
meanings
of
probabilities. Generally, probabilities
in
the
quantum
mechan-
ics
are
defined secondarily from
probability
amplitudes.
The
nondiagonal
parts
in
the
above p
are
called
parts
of
quantum fractuations.
The
inter-
ference
pattern
seen in Fig. 8 is formed due
to
the
effects
of
quantum
fractuations.
The
state
vector I¢) = a
10)
+
(311)
is a
mixture
of
10)
and
11)
in
a sense, however
it
is
not
the
probabilistic
mixture
as seen in
the
form of
p in Fig.
7.
The
form of I¢) affirms
the
states
of
10)
and
11)
simultaneously

59
with
weights
of
a
and
(3,
which
are
not
probabilities,
and
it
does
not
imply
"a
photon
passed
through
either
the
slit-O
or
the
s
lit-I".
The
prob
abilistic
mixture
p never explain
the
interference
pattern.
The
double slit
experiment
symbolically represents
the
decision-making
process which we discussed previously.
Let
us replace
the
term
of
"photon"
by
"the
player B" ,
and
replace
the
context
as
"the
photon
passes
through
the
slit-O (or 1)" by
"the
player B chooses
the
strategy
OB
(or I
B
)".
Then,
the
distribution
shown in Fig. 5 (
or
Fig. 6 ) represents a posterior analysis
by
the
play
er
A who determines
the
player B chose
OB
(or
IB).
Further-
more,
the
distribution
in
Fig. 7 is
int
erp
re
ted
as
the
mixture
of
posterior
analyses corresponding
to
a prior analysis
in
the
conventional game the-
ory.
Th
e existence of
the
two
photon-detectors
in Fig. 7 means
that
the
player A determines
the
player
B's
choice probabilistically.
The
game
the-
ory identifies
this
probabilistic
determination
as
an
uncertainty
the
A holds.
However, we consider a more deep
unc
ertai
nty
where
the
player A
can
never
determine
the
B's choice essentially.
The
distribution
in Fig. 8 represents
a prior analysis
based
on
such
the
unc
erta
inty.
The
mathematical
formalism
in
quantum
mechanics gives
th
e
quantum
uncertainty
with
quantum
fluctuation, which is differe
nt
essentially from
the
classical probability distribution. As
pointed
out
previously, we believe
that
the
quantum
uncertainty
is very similar
to
the
uncert
ai
nty
which
the
player
A holds for
the
another
player
B's
choice. Someone might criticize
that
the
B's
action
is a classical phenomenon, so such
the
uncertainty
should
be
described by classical probabilities. However,
this
stochastic
phenom
enon
is
just
an
objective fact recognized posteriorly from some
statistical
data.
The
uncertainty
in decision-making
should
be
described
with
based
on
the
subjective fact
that
the
player A essentially
can
never
determine
the
B's
choice.
This
subjective fact is
rather
r
ea
listic for
A's
prior analysis
in
his
decision-making.
References
1.
Shafir,
E.
and
Tversky, A.:
Thinking
through
unc
erta
inty: nonconseque
ntial
reasoning a
nd
choice. Cognitive Psychology 24, 449-474 (1992)
2.
Tversky
, A.
and
Shafir, E.:
The
disjun
ction
effect in choice
under
uncert
a
inty
.
Psychological Science, 3,
305-309 (1992)
3.
Croson, R.:
The
disjunction
effect
and
reasoning-based choice
in
games. Or-
ganizational
Behavior
and
Human
Decision Processes 80, 118-133 ( 1999)
4.
Hofstader,
D. R.: Dil
emmas
for
superrational
thinkers,
l
ea
ding
up
to
a luring
lottery. Scientific
American,
6 (1983)
