Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.

а) Выяснить являются ли поля (k, l) и (m, n) полями одного
цвета.
б) На поле (k, l) расположен ферзь. Угрожает ли он полю (m, n)?
в) Аналогично б), но ферзь заменяется на коня.
г) Выяснить, можно ли с поля (k, l) одним ходом ладьи попасть
на поле (m, n). Если нет, то выяснить, как это можно сделать за два
хода (указать поле, на которое приводит первый ход).
д) Аналогично г), но ладья заменяется на ферзя.
е) Аналогично г), но ладья заменяется на слона.
Предполагается, что указанные поля имеют один и тот же цвет.
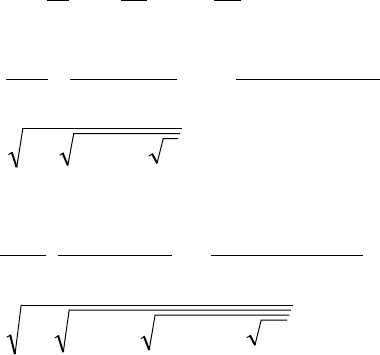
§ 4. Простейшие циклы
77. Дано натуральное число n. Вычислить:
a) 2
n
;
б) n!;
в)
+
+
+
222
1
1...
2
1
1
1
1
1
n
;
г)
nsin...1sin
1
...
2sin1sin
1
1sin
1
++
++
+
+
;
д)
"""!"""
корнейn
2...22 +++
;
е)
n
n
sin...1sin
cos...1cos
...
2sin1sin
2cos1cos
1sin
1cos
++
++
⋅⋅
+
+
⋅
;
ж) nn 3)1(3...63 +−+++ .

78. Даны действительное число a, натуральное число n.
Вычислить:
а) а
n
;
б) а(а+1)…(а+n–1);
в)
))...(1(
1
...
)1(
11
naaaaaa ++
++
+
+ ;
г)
n
2
42
1
...
111
a
aaa
++++
;
д) ))...(2)((
2
nananaa −−− .
79. Вычислить (1+sin 0.1)(1+sin 0.2)…(1+sin 10).
80. Дано действительное число x. Вычислить
!13!11!9!7!5!3
13119753
xxxxxx
x +−+−+− .

81. Даны действительные числа х, а, натуральное число n.
Вычислить
{
aaaaax ++++++
2222
скобокn
))...))((...(( .
82. Дано действительное число х. Вычислить
)63)...(7)(3)(1(
)64)...(8)(4)(2(
−−−−
−−−−
xxxx
xxxx
.
83. Дано действительное число а. Найти:
а) среди чисел 1,
2
1
1+
,
3
1
2
1
1 ++
, … первое, большее а;
б) такое наименьшее n, что
n
1
...
2
1
1 +++
> a.
84. Даны натуральное n, действительное х. Вычислить:
а) xxx
n
sin...sinsin
2
+++ ;
б)
n
xxx sin...sinsin
2
+++ ;
в)
""!""
n
xxx sin...sinsin...sinsinsin
+++ ;
85. Даны действительные числа a, h, натуральное число n.
Вычислить
f(a)+2f(a+h)+2f(a+2h)+…+2f(a+(n–1)h)+f(a+nh),
где
f(x)=(
2
x +1)cos
2
x.
86. Дано натуральное число n.
а) Сколько цифр в числе n.
б) Чему равна сумма его цифр?
в) Найти первую цифру числа n.
г) Найти знакочередующуюся сумму цифр числа n (пусть запись
n в десятичной системе есть
01
...
α
α
α
−kk
; найти
01
)1(...
ααα
k
kk
−++−
−
).
87. Даны натуральное n, m. Получить сумму m последних цифр
числа n.
88. Дано натуральное число n.
а) Выяснить, входить ли цифра 3 в запись числа
2
n .
б) Поменять порядок цифр числа n на обратный.
в) Переставить первую и последнюю цифры числа n.
г) Приписать по единице в начало и в конец записи числа n.
89. Алгоритм Евклида нахождения наибольшего общего
делителя (НОД) неотрицательных целых чисел основан на следующих
свойствах этой величины. Пусть m и n – одновременно не равные нулю
целые неотрицательные числа и пусть m ≥ n. Тогда, если n = 0, то НОД
(n, m) = m, а если n ≠ 0, то для чисел m, n и r, где r – остаток от деления
m на n, выполняется равенство НОД (m, n) = НОД (n, r). Например,
НОД(15, 6) = НОД(6, 3) = НОД(3, 0) = 3.

Даны натуральные числа n, m.
а) Используя алгоритм Евклида, найти наибольший общий
делитель n и m.
б) Найти наименьшее общее кратное n и m.(Как здесь может
помочь алгоритм Евклида?)
90. Даны натуральные числа m и n. Найти такие натуральные p и
q, не имеющие общих делителей, что p/q = m/n.
91. Пусть
,...2,1,/1;1
10
=+==
−
kkkaaa
kk
Дано натуральное число n. Получить
n
a .
92. Пусть
0
21
==
υ
υ
; 5.1
3
=
υ
;
321
2
1
1
−−−
−
+
+
=
iiii
i
i
υυυυ
, i = 4, 5, …

Дано натуральное
n (n ≥ 4). Получить
n
υ
.
93. Пусть
;
0
cx = dx =
1
;
brxqxx
kkk
++=
−− 21
; k = 2, 3, …
Даны действительные q, r, b, c, d, натуральное n (n ≥ 2). Получить
n
x .
94. Пусть
u
1
= u
2
= 0; 0
21
==
υ
υ
;
2
1
2
1
2121
1
−−
−−−−
++
−−
=
ii
iiii
i
u
uu
u
υ
υ
υ
;
2
12
11
++
−
=
−−
−−
ii
ii
i
u
u
υ
υ
υ
, i = 3, 4, …
Дано натуральное n (n ≥ 3). Получить
n
υ
.
95. Пусть
1
10
== aa ;
1
1
2
2
−
−
−
+=
i
i
ii
a
aa
, i = 2, 3, …
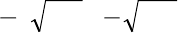
Найти произведение
1410
... aaa ⋅⋅⋅ .
96. Пусть
a
1
= b
2
= 1;
+=
−− 11
2
1
2
1
kkk
aba
;
1
2
1
2
−−
+=
kkk
bab , k = 2, 3, …
Дано натуральное n. Найти
k
n
k
k
ba
∑
=1
*).
*) Выражение
k
n
k
k
ba
∑
=1
есть краткая запись суммы
nn
baba ++...
11
;
вообще
∑
=
n
mk
k
f
обозначает при n ≥ m сумму
nm
ff ++... ; при n < m
выражение смысла не имеет.
97. Пусть

x
1
= y
1
= 1; x
i
= 0.3x
i–1
;
y
i
= x
i–1
+ y
i–1
, i = 2, 3, …
Дано натуральное n. Найти
∑
=
+
n
i
i
i
y
x
1
1
.
98. Пусть
a
1
= b
1
= 1; a
k
= 3b
1−k
+ 2a
1−k
;
b
k
=2a
1−k
+
1−k
b , k = 2, 3, …
Дано натуральное n. Найти
()
∑
=
++
n
i
kk
k
kba
1
22
!1
2
.
99. Пусть
,...3,2,2
;2,,
1
2
1
1111
=+=
+===
−−
−−
kbab
abavbua
kkk
kkk
