Абрамов С.А., Гнездилова Г.Г., Капустина Е.Н., Селюн М.И. Задачи по программированию
Подождите немного. Документ загружается.

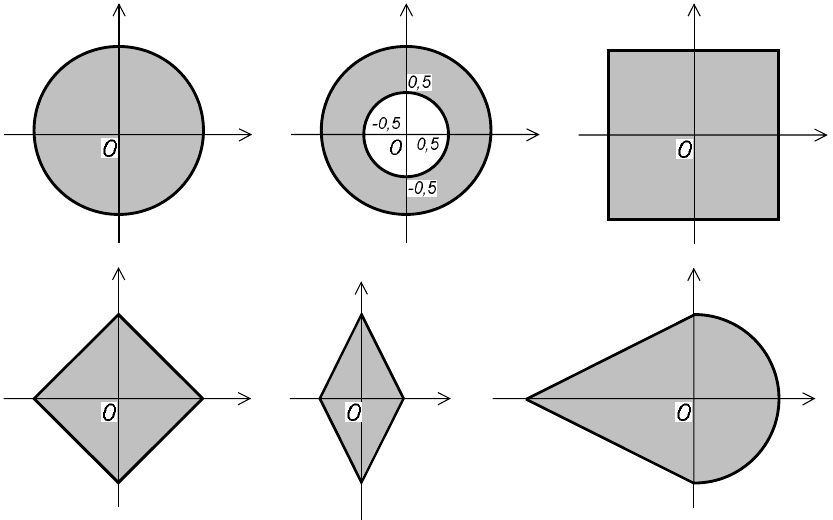
59. Даны действительные числа x, y. Определить, принадлежит
ли точка с координатами
x, y заштрихованной части плоскости (рис. 2,
а—2, к).
1
x
1
y
-1
-1
а
1
y
-1
-1 1
x
б
в
1
y
1
-1
-1
x
1
y
1
-1
-1
x
г
x
1
y
0,5
-1
-0,5
д
1
x
1
y
-1
-2
е

60. Пусть D – заштрихованная часть плоскости (рис. 1, а—3, е)
и пусть
u определяется по x и y следующим образом (запись (x, y)∈D
означает, что точка с координатами
x, y принадлежит D):
ж
-1 1
-1
2
y
x
з
x
-2
1-1
y
1
и
-2 1
x
1
y
-1
1
x
y
-1
к
Рис. 2
−
∈+
=
+
∈−
=
−
∈−
=
+
∈−
=
∈−
=
∈
=
случае. противном в
,),( если ,
е)
случае; противном в
,),( если ,1
д)
случае; противном в 1
,),( если ,1
г)
случае; противном в 7
,),( если
в)
случае; противном в
,),( если ,3
б)
случае; противном в
,),( если ,0
а)
2
2
2
yx
Dyxyx
u
yx
Dyxx
u
x
Dyxx
u
xy
Dyxyx
u
y
Dyx
u
x
Dyx
u
Даны действительные числа
x, y. Определить u.
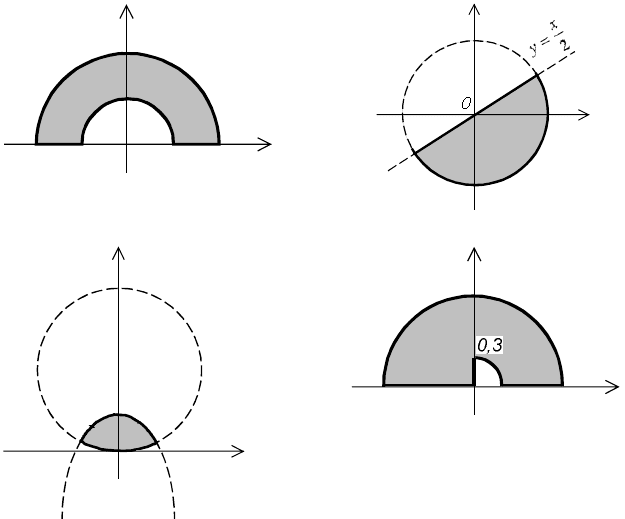
2
1
-1-2 0 1 2
y
x
а
1
y
-1
-1
1
x
б
1
22
=+ yx
1 0
y
-1
x
в
1)1(
22
=−+ yx
2
1 xy −=
1
1
0 0,3 1-1
y
x
г

1
y
-1
-1
1
x
д
xy =
xy −=
1
0
y
x
е
2
xy =
x
ey =
x
ey
−
=
Рис.3
§ 3. Простейшая целочисленная арифметика
61. Дано действительное число х. Получить целую часть *)
числа х; затем – число х, округленное до ближайшего целого; затем –
число x без дробных цифр.
*) Целой частью числа х, обозначаемой [х], называется наибольшее
целое, не превосходящее х, так, [3.14] = 3, [3 ] = 3, [–3. 1 4] = –4,
[– 3] = –3.
62. Определить, является ли данное целое число четным.
63. Определить, верно ли, что при делении неотрицательного
целого числа а на положительное целое число b получается остаток,
равный одному из двух заданных чисел r или s.
64. Дано натуральное число n (n>99). Определить число сотен в
нем.
65. Дано натуральное число n (n>99). Выяснить, верно ли, что n
2
равно кубу суммы цифр числа n.
66. Даны целые числа k, m, действительные числа x, y, x. При k<
m
2
, k = m
2
или k>m
2
заменить модулем соответственно значения x, y
или z, а два других значения уменьшить на 0.5.
67. Дано натуральное число n (n ≤100).
а) Сколько цифр в числе n?
б) Чему равна сумма его цифр?
в) Найти последнюю цифру числа n.
г) Найти первую цифру числа n.
д) В предположении, что n ≥10, найти предпоследнюю цифру
числа n.
68. Дано натуральное число n (n ≤9999).
а) Является ли это число палиндромом (перевертышем) с уче-
том четырех цифр, как, например, числа 2222, 6116, 0440 и т. д.?
б) Верно ли, что это число содержит ровно три одинаковые
цифры, как, например, числа 6676, 4544, 0006 и т. д.?
в) верно ли, что все четыре цифры числа различны?
69. Часовая стрелка образует угол
ϕ
с лучом, проходящим
через центр и через точку, соответствующую 12 часам на циферблате,
0 <
ϕ
≤ 2
π
. Определить значение угла для минутной стрелки, а также
количество часов и полных минут.
70. Даны целые числа m, n (0 < m ≤ 12, 0 ≤ n < 60),
указывающие момент времени: «m часов, n минут». Определить
наименьшее время (число полных минут), которое должно пройти до
того момента, когда часовая и минутная стрелки на циферблате:
а) совпадут;
б) расположатся перпендикулярно друг другу.
71. Дано действительное число а. Вычислить f(a), где f –
периодическая функция с периодом 1.5, совпадающая на отрезке
[0,1.5]:
а) с функцией x
3
–2.25x;
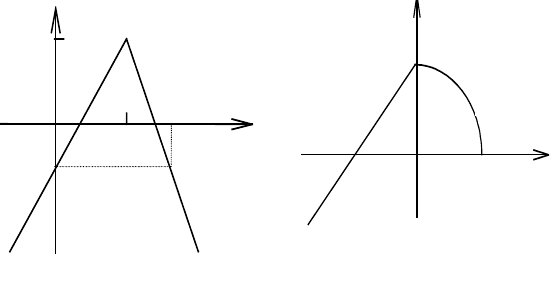
б) с функцией, график которой изображен на рис. 4.
x
1
1
1
5
,
−
0
5
,
Рис.
4
y
1
x
1
0
−
1
yx=−1
3
Р и с.5
72. Дано действительное число а. Вычислить f(a), где f –
периодическая функция с периодом 2, совпадающая на отрезке [–1,1]:
а) с функцией –x
2
+1;
б) с функцией, график которой изображен на рис. 5.
73. Даны целые числа k, l. Если числа не равны, то заменить
каждое из них одним и тем же числом, равным большему из исходных,
а если равны, то заменить числа нулями.
74. Дано натуральное n (n ≤ 100), определяющее возраст
человека (в годах). Дать для этого числа наименования «год», «года»
или «лет»: например, 1 год, 23 года, 45 лет и т. д.
75. Доказать, что любую целочисленную денежную сумму,
большую 7 руб., можно выплатить без сдачи трешками и пятерками.
Для данного n > 7 найти такие целые неотрицательные a и b, что 3a +
5b = n.
76. Поле шахматной доски определяется парой натуральных
чисел, каждое из которых не превосходит восьми: первое число –
номер вертикали (при счете слева направо), второе – номер
горизонтали (при счете снизу вверх). Даны натуральные числа k, l, m,
n, каждое из которых не превосходит восьми. Требуется:
