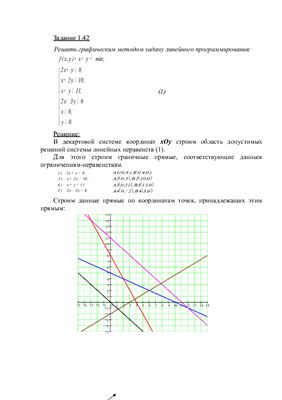
Задание 1.50.
Решить графическим методом задачу линейного программирования:
Задание 2.60.
Четыре предприятия А1, А2, А3, А4 изготавливают продукцию в количествах а1=290, а2=210, а3=170, а4=180 соответственно, которую используют предприятия В1, В2, В3, В4 в количествах b1=230, b2=280, b3=150, b4=.
190. Необходимо составить оптимальный план перевозок, если матрица стоимости имеет вид.
Задание 3.70.
На предприятии имеются бревна длиной L=6,6 м, которые необходимо разрезать на заготовки длиной l1=2,3 м, l2=1,8 м, l3=2,1 м в количестве р1=600, р2=720, р3=570 соответственно.
Необходимо составить оптимальный план раскройки материала, который обеспечивает минимальные отходы, при условии выполнения плана по выходу заготовок.
Задание 4.80.
Техническое устройство может находиться в одном из трех состояний S0, S1, S.
2. Интенсивность потоков, переводящих устройство из состояний в состояние заданы в таблице.
Необходимо построить размеченный граф состояний, записать систему уравнений Колмогорова, найти финальные вероятности и сделать анализ полученных решений.
Задание 5.90.
Разложить функцию в ряд Фурье в интервале.
Задание 6.100.
Найти по формуле Даламбера уравнение формы однородной бесконечной струны, определяемой волновым уравнением, если в начальный момент времени t=0 форма струны и скорость ее точек определяются функциями .
Решить графическим методом задачу линейного программирования:
Задание 2.60.
Четыре предприятия А1, А2, А3, А4 изготавливают продукцию в количествах а1=290, а2=210, а3=170, а4=180 соответственно, которую используют предприятия В1, В2, В3, В4 в количествах b1=230, b2=280, b3=150, b4=.
190. Необходимо составить оптимальный план перевозок, если матрица стоимости имеет вид.
Задание 3.70.
На предприятии имеются бревна длиной L=6,6 м, которые необходимо разрезать на заготовки длиной l1=2,3 м, l2=1,8 м, l3=2,1 м в количестве р1=600, р2=720, р3=570 соответственно.
Необходимо составить оптимальный план раскройки материала, который обеспечивает минимальные отходы, при условии выполнения плана по выходу заготовок.
Задание 4.80.
Техническое устройство может находиться в одном из трех состояний S0, S1, S.
2. Интенсивность потоков, переводящих устройство из состояний в состояние заданы в таблице.
Необходимо построить размеченный граф состояний, записать систему уравнений Колмогорова, найти финальные вероятности и сделать анализ полученных решений.
Задание 5.90.
Разложить функцию в ряд Фурье в интервале.
Задание 6.100.
Найти по формуле Даламбера уравнение формы однородной бесконечной струны, определяемой волновым уравнением, если в начальный момент времени t=0 форма струны и скорость ее точек определяются функциями .