Золотаревский В.С. Механические свойства металлов
Подождите немного. Документ загружается.


ные
трещины
обычно
встречаются
при
относительно
низких
тем
пературах
и
высоких
напряжениях.
С
повышением
температуры
и
снижением
действующего
напряжения
их
число
уменьшается,
но
зато
на
межзеренных
границах
наблюдается
все
больше
мелких
пор
круглого
или
эллиптического
сечения.
Зародышами
этих
пор
или
пустот
могут
быть
микронесплошности
на
границах
зерен,
имевшиеся
еще
до
начала
ползучести.
Поры
легко
могут
зарож
даться
и
в
процессе
ползучести.
Для
однофазных
материалов
наиболее
вероятными
считают
два
механизма.
Первый
предполагает
межзеренное
проскальзывание
вдоль
границы
со
ступенькой
(см.
рис,
163,в).
Такие
ступеньки
высотой
до
-40
нм
всегда
имеются
на
границах.
Кроме
того,
сту
пеньки
могут
появиться
там
в
результате
деформации
на
концах
полос
скольжения.
Второй механизм
исходит
из
возможности
образования
и
раз
вития
пор
в
результате
слияния
вакансий.
Рост
пор,
возникших
по
первому
механизму,
по
крайней
мере
на
начальных
стадиях,
также
идет
за
счет
стока
туда
вакансий.
Разрастаются
далеко
не
все
возникающие
при
ползучести
микропоры.
Некоторые
из
них,
не
достигшие
достаточно
большого
размера,
«залечиваются».
Пора
становится
устойчивой,
когда
ее
радиус
r >2,(/S,
(100)
где
S -
растягивающее
напряжение;
'(
-
поверхностная
энергия.
Из
формулы
(100)
следует,
что
чем
выше
напряжение,
тем
меньше
размер
устойчивой
поры.
В
гетерофазных
сплавах
образование
межкристаллитных
пус
тот
в
значительной
мере
связано
с
частицами
избыточных
фаз
на
границах.
Они
могут
затруднять
межзеренные
смещения,
но
если
последние
все-таки
будут
происходить,
то
на
межфазной
грани
це
возникнет
несплошность.
Вероятность
ее
образования
больше,
если
поверхностная
энергия
на
границе
матрица
-
избыточная
фаза
велика
и частица
имеет
компактную
форму.
Частицы
избы
точных
фаз
содержатся
даже
в
относительно
чистых
металлах,
и
поэтому
их роль
в
межзеренном
разрушении
важна
для
любых
материалов.
Чисто
межзеренное
разрушение
при
ползучести
обычно
про
исходит
после
относительно
небольшой
деформации
(8<1+5 %).
Оно
облегчено
в
условиях
высоких
температур
и
низких
напряже-
310

ний
(малой
скорости
ползучести),
когда
есть
возможности
и
вре
мя
для
вакансионного
развития
межкристаллитных
пустот.
Меж
зеренное
разрушение
опасно
также
в
области
относительно
низ
ких
температур,
когда
еще
мала
скорость
возврата
и
ограничены
возможности
миграции
границ.
При
промежуточных
температурах
пластичность
максимальна,
так
как
здесь
межзеренное
разрушение
затруднено
и
степень
внут
ризеренной
деформации
достигает
значительной
величины.
5.
Испытания
на
длительную
прочность
Предел
ползучести
характеризует
напряжение,
под
действием
которого
материал
может
длительное
время
работать,
не
подвер
гаясь
значительной
деформации.
Однако
он
ничего
не
говорит
о
сопротивлении
материала
разрушению
при
длительном
воздей
ствии
температуры
и напряжения.
Для
оценки
этой
сопротивляе
мости
проводят
специальные
испытания
на
длительную
прочность
(ГОСТ
10145
- 81).
В
результате
испытаний
определяют
предел
длительной
nрочности
-
условное
напряжение,
под
действием
которого
материал
при
данной
температуре
разрушается
через
заданный
промежуток
времени.
.
Иногда
предел
длительной
прочности
не
рассчитывают,
огра
ничиваясь
установлением
соответствия
между
временем
до
раз
рушения
(долговечностью)
под
действием
заданного
напряжения
и
нормой
времени,
устанавливаемой
стандартом
или
техничес
кими
условиями
на
металлопродукцию.
Методика
проведения
испытания
близка
к
методике
испыта
ний
на
ползучесть.
Используются
те
же
схемы
нагружения
(обыч
но
растяжение)
и
те
же
испытательные
машины.
Основные
ци
линдрические
образцы
стандартизованы.
Они
должны
иметь
ра
бочую
часть
диаметром
d
o
=
5,
7
или
10
мм
и
расчетную
длину
'0=5d
o
или
10d
o
.
Допускаются
другие
пропорциональные
образцы,
но
их
диаметр
должен
быть
не
меньше
3
мм.
У
плоских
образцов
'о
=
5,65..JF'a,
где
F
o
-
начальная
площадь
поперечного
сечения.
Конструкция
головок
и
способ
их
крепления
в
захватах
аналогичны
применяе
мым
при
испытаниях
на
ползучесть.
311

Абсолютные
размеры
образцов
могут
заметно
сказываться
на
характеристиках
длительной
прочности,
в
первую
очередь
из-за
разного
отношения
их-поверхности
к
объему.
У
образцов
малого
диаметра
поверхностный
слой,
в
котором
преимущественно
об
разуются
трещины,
относительно
более
развит,
и
поэтому
их
долговечность
может
быть
ниже,
чем
у
больших
образцов.
Помимо
гладких,
используют
образцы
с
надрезом,
чаще
всего
У-образным
кольцевым
с
углом
раскрытия
60
или
450
Для
определения
предела
длительной
прочности
необходимо
провести
испытание
нескольких,
по
крайней
мере
пяти-шести
образцов
при
разных
напряжениях.
Основным
результатом
испы
тания
каждого
образца
является
время
до
разрушения
.р
при
за
данном
напряжении
0".
Связь
между.р
и
о"
хорошо
аппроксимиру
ется
уравнением
(101)
где
В
и
т
-
коэффициенты.
В
логарифмических
координатах
эта
зависимость
прямолиней
на
и,
следовательно,
дает
возможность
экстраполировать
резуль
таты
на
более
длительное
время.
Определив
время
до
разрушения
образцов,
находившихся
под
напряжением,
заведомо
большим
предполагаемого
предела
длительной
прочности
(чтобы
сокра
тить
время
испытания),
строят
по
экспериментальным
точкам
прямую
19
о"
-
19
.р
и
после
ее
экстраполяции до
заданного
време
ни
оценивают
величину
этого
предела
(рис.
164,
кривая
1).
По
стандарту
рекомендуемый
допуск
по
времени
составляет
от
50
до
10000
ч
и
определяется,
как
и
в
случае
предела
ползучести,
тре
бованиями
к
испытываемому
материалу.
Иногда
зависимость
19
о"
-
19.
характеризуется
точкой
пере
лома
(см.
рис.
164,
кривая
2). dHa
соответствует
переходу
от
внутрикристаллитного
или
смешанного
разрушения
к
полностью
межкристаллитному
разрушению
при
низких
напряжениях.
В
та
ких
случаях
экстраполяцию
можно
проводить,
если
надежно
ус
тановлен
наклон
прямой
в
области
межкристаллитного
разруше
ния.
Обработку
первичных
результатов
испытаний
и
определение
предела
длительной
прочности,
как
и
предела
ползучести,
следу
ет
про
водить
с
использованием
статистических
методов.
В
частно
сти,
построение
прямых
в
логарифмических
координатах
(1gO"~
Igv
n
,YCT'
19
о"
-lg.)
нужно
выполнять
методом
наименьших
квадра-
312

тов
С
оценкой
величины
доверитель-
lqб
ного
интервала.
Обозначение
предела
длительной
прочности
cr
сопровождают
двумя
индексами:
вверху
записывают
тем
пературу
испытания,
ос,
внизу
-
заданную
долговечность,
ч.
Напри-
мер,
crrggo
-
предел
1000-'1
прочно
сти
при
900
ос.
Помимо
предела
длительной
прочности,
в
этих
испытаниях
оце
нивают
характеристики
пластично-
Рис.
164.
Схема
определения
предела
длительной
прочности
сти
-
относительное
удлинение
и
сужение.
Часто
деформация
фиксируется
и
в
процессе
испытания.
В
результате
может
быть
построена
полная
кривая
ползучести,
а
по
ней
определена
величина
относительного
удлинения
к
концу
стадии
установившейся
ползучести
(см.
рис.
152,
Оп),
Эту
величину
считают
характеристикой
запаса
длительной
пластичности
мате
риала,
она
обычно
значительно
меньше
конечного
удлинения
на
стадии
разрушения.
При
высокотемпературных
испытаниях
на
длительную
проч
ность,
когда
образцы
доводят
до
разрушения,
каждый
из
них
последовательно
проходит
все
три
стадии
ползучести
и
величина
предела
длительной
·прочности
определяется
поведением
мате
риала
на
всех
стадиях,
в
том
числе
на
стадии
разрушения.
Факто
ры,
препятствующие
развитию
пор
и
трещин,
способствуют
по
вышению
предела
длительной
прочности.
Таким
образом,
предел
длительной
прочности
характеризует
способность
материала
про
тивостоять
разрушению
при
длительном
воздействии
температу
ры
и
напряжения.
6.
Испытания
на
релаксацию
напряжений
Релаксацией
называют
самопроизвольное
уменьшение
напря
жений
в
материале
при
неизменном
значении
величины
его
об
щей
деформации.
Это
вызвано
переходом
упругой
деформации
в
пластическую.
Релаксация
напряжения
-
широкое
понятие.
Мы
уже
не
раз
встречались
с
ним,
рассматривая
процессы
пластической
дефор-
313

мации
и
разрушения.
Но
до
сих
пор
речь
шла
о
местных
релакса
циях
напряжений
в
отдельных
участках
материала.
При
испыта
ниях
на
релаксацию
оценивают
уменьшение
макронапряжений
во
всем
образце.
Типичным
примером
детали,
работающей
в
ус
ловиях
релаксации
напряжений,
является
болт
фланцевого
со
единения.
Плотность
этого
соединения
определяется
усилием
на
тяга
болта,
который
создается
вследствие
упругой
деформации
болта.
С
течением
времени
натяг
болта
(уровень
напряжений)
ос
лабевает,
так
как
часть
упругой
деформации
переходит
в
пласти
ческую.
Особенно
быстро
и
значительно
релаксируют
напряжения
при
повышенных
температурах,
когда
пластическая
деформация
об
легчается.
Кривая
изменения
напряжения
во
времени
(кривая
ре
лаксации)
в
образце,
деформированном
на
постоянную
величи
ну,
имеет
вид,
схематично
показанный
на
рис.
165.
Спад
напря
жений
особенно
интенсивен
в
первые
часы.
С
течением
времени
кривая
асимптотически
приближается
к
какому-то
определенно
му
значению
напряжения.
Итак,
испытания
на
релаксацию
необходимо
проводить
в
сле
дующих
условиях:
т
= const,
а"#
const,
е
улр
"#
const,
е
л
"#
const,
е
о
=
еynр
+
ел
= const,
где
т
-
температура;
а
-
напряжение
в
образце;
е
улр
,
е
п
-
упругая
и
пластическая
деформация;
е
о
,-
общая
деформация
образца.
Условие
постоянства
общей
деформации
можно
записать
как
де
о
=
о.
Тогда
!!.е
о
=
де
+
де
=
О
или
-де
=
де
.
Так
как
ynр n
ynр
п
деynр
=да/
Е,
Рис.
165.
Кривая
релаксации
напряжений
314
то
-да
=Еде
или
п
да
=
а
-а
=
Е(е
-
ей)
о
п
п
'
(102)
где
а
о
и
e~
-
напряжение
и
деформация
в
момент
начала
релаксации
напряжений.
Из
формулы
(102)
следует
неизбежность
спада
напряжений
из-за
увеличения
доли
пластической
деформации.
Зависимость
величины
релаксации
напря.:.
жений
да
от
времени
часто
подчиняется

логарифмическому
закону:
dcr
=
a,lg(1
+
K't),
где
а,
и
К
-
коэффициенты,
не
зависящие
от
времени,
Этот
закон
можно
вывести
из
общего
уравнения
релаксации
напряжений
как
термически
активируемого
процесса:
dcr/d't
=
к
exp[-(Q-B
cr)/kn,
(103)
где
энергия
активации
(Q-Bcr)
зависит
от
напряжения.
Как
видно
из
формулы
(103),
скорщ:ть
релаксации
dcr/d't
рас
тет
экспоненциально
с
повышением
температуры.
Механизм
релаксации
связан
с
постепенным
перемещением
дислокаций
за
счет
поперечного
скольжения
и
переползания
даже
в
условиях
снижающегося
внешнего
напряжения.
Как
и
при
пол
зучести,
при
высокотемпературной
релаксации
напряжений
пла
стическая
деформация
сопровождается
образованием
субзерен
ной
структуры
и
смещениями
по
границам
кристаллитов.
Ско
рость
релаксации
обычно,
прямо
пропорциональна
скорости
пол
зучести:
чем
выше
сопротивление
ползучести,
тем
больше
релак
сационная
стойкость.
Испытания
на
релаксацию
про
водят
по
схемам
растяжения,
изгиба
и
кручения.
Схема
установки
для
испытании
на
релаксацию
при
растяже
нии
показана
на
рис.
166.
Образец
4
крепится
в
захватах
2
и
5,
помещается
в
печь
6
и
нагружается
рычагом
7
от
электродвигате
ля
11
через
пружину
/О.
На
границах
расчетной
длины
образца
устанавливают
измеритель
де-
формации
З.
При
удлинении
об
разца
на
величину
допуска
кон
такт
J
замыкает
цепь
регулято
ра
J
2,
двигатель
меняет
направ
ление
вращения
и
ослабляет
пружину
10.
Спад
напряжения
в
образце
при
водит
к
его
укоро
чению,
и,
когда
длина
образца
вновь
станет
равной
начальной,
контакт
J
размыкается,
образец
снова
начинает
удлиняться
и
т.
д.
Кривая
релаксации
записыва
ется
на
барабане
8,
который
Рис.
166.
Схема
установки для
испьпаний
на
релаксацию
напряжений
(и.
Г.
Дондик)
315

вращается
двигателем
9.
Широкое
распространение
получил
метод
и.
А.
Одинга,
где
релаксация
оценивается
на
кольцевых
образцах,
расчетная
часть
которых
ВАВ
(рис.
167)
имеет
равное
сопротивление
изгибу.
На
пряжение
в
образце
создается
установкой
клина
К
в
прорезь
сс.
Утолщенные
части
образца
ВС
и
.
вс
в
релаксации
не
участвуют.
Они
только
передают
усилие
от
клина
к
расчетной
части
кольца.
Величина
создаваемых
там
напряжений
определяется
толщиной
клина
t.
Она
больше
ширины
прорези,
поэтому
общая
начальная
деформация
eo=t-a,
а
начальное
напряжение
в
наружных
волок
нах
расчетной
части
а
о
=
ЕАе
о
,
где
Е
-
модуль
нормальной
упругости;
А
-
коэффициент,
свя
занный
с
перемещением
утолщенных
концов
кольца
в
процессе
деформации,
равный
0,000583
мм.
После
выдержки
образца
в
печи
при
заданной
температуре
в.
течение
определенного
времени
его
вынимают,
охлаждают,
уда
ляют
клин
из
прорези
и
измеряют
ширину
се,
которая
теперь
меньше
а.
Величина
остаточного
напряжения
а
ост
=ЕАl1е,
где
l1е
-
разница
между
получаемой
после
испытания
деформа
цией
и
е
о
.
Рис.
]
67.
Кольцевой
образец
для
испытnния
на
релаксацию
(и.
А.
Одимг)
316

После
этого
рассчитывают
величину
релаксации
напряжений
.1.0"
=
0"0
-
о"
ост.
По
результатам
измерений
.1.0"
в
функции
времени
вьщержки
образца
в
печи
строят
кривую
релаксации.
В
качестве
характеристики
релаксационной
стойкости
принимают
величину
падения
напряжения
.1.0"
за
заданное
время
(200-3000
ч).
7.
ВЛИАние
легироваНИА
и
структуры
на
характеристики
жаропрочности
Повышение
характеристик
жаропрочности
(пределов
ползу
чести
и
длительной
прочности,
релаксационной
стойкости
при
высоких
температурах)
достигается
теми
же
способами,
которые
были
обсуждены
в
гл.
V
применительно
к
прочностным
свойствам
при
статических
испытаниях.
Но
влияние
легирования
и
струк
турных
пара
метров
на
жаропрочность
характеризуется
рядом
спе
цифических
особенностей,
которые
и
будут
рассмотрены.
Повышение
жаропрочности
при
переходе
от
чистых
металлов
к
сплавам
достигается
за
счет
образования
твердых
растворов
на
базе
основного
металла
и
частиц
избыточных
фаз.
При
выборе
основы
следует
учитывать,
что
уровень
жаропрочности
чистого
металла
связан
с
температурой
его
плавления.
Чем
она
выше,
тем
больше
прочность
межатомных
связей,
меньше
скорость
само
диффузии
и,
следовательно,
меньше
при
той
же
температуре
ско
рость
ползучести.
Исходя
из
этих
соображений,
температура
со
лидуса
сплавов
также
должна
быть
по
возможности
выше.
Если
температура
плавления
сплава
значительно
ниже,
чем
металла
основы,
то
при
высоких
температурах
чистый
металл
может
ока
заться
прочнее
сплава.
Растворенные
атомы
повышают
сопротивление
ползучести
за
счет
их
упругого
взаимодействия
с
дислокациями
и
дефектами
упаковки,
а
также
в
результате
их
влияния
на
диффузионные
процессы.
Эффект
влияния
растворимых
легирующих
элементов
может
быть
значительным.
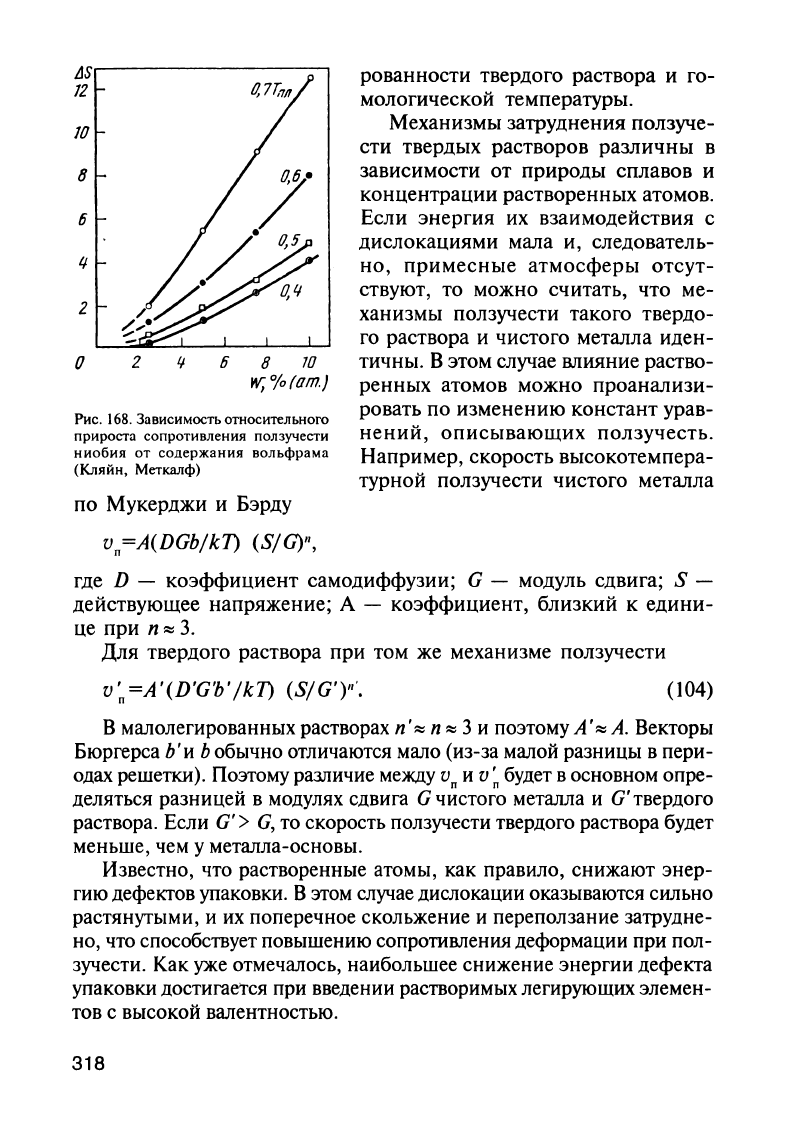
На
рис.
168
показано,
как
зависит
от
концентрации
вольфрама
в
твердом
растворе
на
основе
ниобия
относительный
прирост
сопротивления
ползучести
.1.5=
(О"спл
- O"Nb)/O"Nb'
где
О"спл
И
O"Nb
-
напряжения,
при
которых
в
сплаве и
чистом
ниобии
v =10-5
c-
I
.
Видно,
что
.1.5
растет
с
повышением
леги-
п.уст.
317
AS
12
10
8
б
"
2
О
2
'1
б
8
70
w;o;o(om.)
Рис.
168.
Зависимость
относительного
прироста
сопротивления
ползучести
ниобия
от
содержания
вольфрама
(Кляйн,
Меткалф)
по
Мукерджи
и
Бэрду
v
п
=А(DGЬ/k1)
(S/G)",
рованности
твердого
раствора
и
го
мологической
температуры.
Механизмы
затруднения
ползуче
сти
твердых
растворов
различны
в
зависимости
от
природы
сплавов
и
концентрации
растворенных
атомов.
Если
энергия
их
взаимодействия
с
дислокациями
мала
и,
следователь
но,
примесные
атмосферы
отсут
ствуют, то
можно
считать,
что ме
ханизмы
ползучести
такого
твердо
го
раствора
и
чистого
металла
иден
тичны.
В
этом
случае
влияние
раство
ренных
атомов
можно
проанализи
ровать
по
изменению
констант
урав
нений,
описывающих
ползучесть.
Например,
скорость
высокотемпера
турной
ползучести
чистого
металла
где
D -
коэффициент
самодиффузии;
G -
модуль
сдвига;
S -
действующее
напряжение;
А
-
коэффициент,
близкий
к
едини
це
при
n~
3.
Для
твердого
раствора
при
том
же
механизме
ползучести
v~=A'(D'G'b'/k1)
(S/G')"'.
(104)
в
малолегированных
растворах
n'
~
n
~
3
и
поэтому
А
'
~
А.
Векторы
Бюргерса
Ь'и
Ь
обычно
отличаются
мало
(из-за
малой
разницы
в
пери
одах
решетки).
Поэтому
различие
между
v
п
и
v
~
будет
в
основном
опре
деляться
разницей
в
модулях
сдвига
G
чистого
металла и
G'
твердого
раствора.
Если
G' >
G,
то
скорость
ползучести
твердого
раствора
будет
меньше,
чем
у
металла-основы.
Известно,
что
растворенные
атомы,
как
правило,
снижают
энер
гию
дефектов
упаковки.
В
этом
случае
дислокации
оказываются
сильно
растянутыми,
и
их
поперечное
скольжение
и
переползание
затрудне
но,
что
способствует
повышению
сопротивления
деформации
при
пол
зучести.
Как
уже
отмечал
ось,
наибольшее
снижение
энергии
дефекта
упаковки
достигается
при
введении
растворимых
легирующих
элемен
тов
с
высокой
валентностью.
318

Если
n'
или
А'
в
уравнении
(104)
зависят
от
энергии
дефектов
упаковки,
то тогда
А'<
А,
и
это
будет
вызывать
соответствующее
уменьшение
скорости
ползучести.
Коэффициент
диффузии
при
образовании
твердых
растворов
может
изменяться
по-разному.
В
малолегированных
растворах
п'
является
коэффициентом
самодиффузии
атомов
растворителя
в
растворе.
Он
может
и
увеличиваться,
и
уменьшаться
в
присут
ствии
растворенных
атомов.
При
этом
добавка
быстро
диффунди
рующего
компонента
увеличивает
коэффициент
самодиффузии
основного
металла.
Более
сложно
предсказать
изменение
D'
концентрированных
твердых
растворов.
Поскольку
в
таких
растворах
количество
ато
мов
А
и
В
близко,
следует
определять
некий
средний
коэффици
ент
диффузии
D,
являющийся
функцией
коэффициентов
диф
фузии
компонентов
А
и
В
в
твердом
растворе
АВ.
Существующие
методы
расчета
D
пока
несовершенны.
Рассмотрим
теперь
особенности
высокотемпературной
ползу
чести
твердых
растворов
с
большой
энергией
взаимодействия
растворенных
атомов
с
дислокациями.
В
таких
растворах
на
дис
локациях
образуются
примесные
атмосферы,
и
механизм
ползу
чести
может
существенно
измениться.
Если
в
чистых
металлах
при
ползучести
с
возвратом
скорость
скольжения
дислокаций
значи
тельно
больше
скорости
переползания,
то
в
твердых
растворах
наиболее
медленным
и,
следовательно,
контролирующим
ско
рость
ползучести
может
стать
скольжение
дислокаций
с
примес
ными
атмосферами
-
вЯЗICое
скольжение
дислокаций.
Если
допус
тить,
что
скорость
ползучести
при
таком
движении
дислокаций
определяется
скоростью
перемещения
атмосферы,
т.е.
скоростью
миграции
растворенных
атомов
под
действием
силы
притяжения
дислокации,
то
v
n
=
(п
А
/kTC
o
)
Sbexp
(-
W/k1) ,
(105)
где
п
А
-
коэффициент
диффузии.
растворенных
атомов
в
твердом
растворе
концентрации
СО'
W -
энергия
связи
этих
атомов
с
дислокацией;
S -
действующее
напряжение.
Такая
модель
вязкого
скольжения
дислокаций
при
ползучести
должна
реализоваться
при
низких
скоростях
движения
дислока
ций
и
достаточно
высоких
температурах,
если
внешняя
сила,
дей
ствующая
на
единицу
Д/lИНЫ
дислокации,
меньше силы
притя
жения
атмосферы.
В
установившемся
режиме
скорость
v
прямо
319
