Золотаревский В.С. Механические свойства металлов
Подождите немного. Документ загружается.


Уменьшение
n
при
переходе
от
логарифмической
к
неустано
вившейся
высокотемпературной
ползучести
можно
понять
с
по
зиций
модели
истощения.
Действительно,
если
процессы
возвра
та
успевают
проходить
более
полно,
то,
по
крайней
мере, часть
дислокационных
отрезков
после
первой
активации
может
стать
способной
к
повторному
перемещению,
что
вызовет
дополни
тельную
деформацию
и
прирост
V
п
•
Одна
из
дислокационных
моделей,
дающих
кубический
закон
ползучести
(89),
сводится
к
следующему.
Рассмотрим
небольшую
область
кристалла.
Уровень
напряжений
в
этой
области
определя
ется
наличием
дислокаций
в
соседних
участках.
Переход
одной
дислокации
в
более
удаленные
области
(любым
способом)
умень
шает
уровень
напряжения
в
рассматриваемом
объеме
на какую
то
величину
ДSl.
Наоборот,
если
подобная
же
дислокация
прихо
дит
в
соседнюю
область
и
остается
там
(закрепляется
упругим
полем
скопления
у
какого-либо
барьера),
то
уровень
напряжения
в
интересующей
нас
области
повысится
на
ДSl.
Ползучесть
(пластическая
деформация)
в
этом
объеме
будет
идти,
если
обеспечена
возможность
движения
дислокаций.
Пред
полагается,
что
при
неустановившейся
высокотемпературной
ползучести
источники
дислокаций
могут
работать
(генерировать
новые
петли
дислокаций)
вследствие
уменьшения
запирающего
напряжения
из-за
непрерывного
ухода
дислокаций
из
скопления
путем
поперечного
скольжения
и
переползания.
Статистический
расчет
показывает,
что
с
учетом
поперечного
скольжения
и
переползания
после
совершения
n
беспорядочно
чередующихся
переходов
дислокаций
из
соседних
областей
вели
чина
напряжений
в
нашем
объеме
повысится до
n1/2ДSl.
Эта
вели
чина
может
оказаться
достаточной
для
приведения
в
действие
дислокационных
источников.
Величина
n
l
/2
ДS
I=qо,
где
q -
наклон
кривой
растяжения
S-o
при
данном
уровне
на
пряжения.
Тогда
n = (qo
/ДSl)2.
Если
уход
дислокаций
из
скоплений
происходит
с
постоянной
частотой
00,
то
для
n
перемещений
требуется
время
n/оо
и,
следо
вательно,
частота
действия
дислокационных
источников
будет
00/
n.
Отсюда
290

После
интегрирования
получаем
8 =
13,;'13.
Принципиально
ползучесть
на
установившейся
стадии
не
от
личается
от
неустановившеЙся.
Установившаяся
стадия
рассмат
ривается
как
некое
равновесное
состояние,
подготовленное
не
установившейся
ползучестью.
Элементарные
процессы,
идущие
на
обеих
стадиях,
одинаковы,
различна
только
полнота
их
проте
кания.
В
металлах
скорость
установившейся
ползучести
контроли
руется
обычно
наиболее
медленным
процессом
переползания
дислокаций.
Пластическая
деформация
при
ползучести
вызывает
увеличе
ние плотности
дислокаций
и
деформационное
упрочнение.
В
то
же
время
возврат
при
водит
к
уменьшению
плотности
дислока
ций
и
разупрочнению
металла.
В
результате
при
высокотемпера
турной
ползучести
в
металле
формируется
полигонизованная
суб
структура.
Основные
процессы,
определяющие
возврат,
-
поперечное
скольжение
и
переползание
дислокаций.
При
относительно
ма
лом
времени
выдержки,
когда
переползание
дислокаций
еще
не
успевает
проходить
в
достаточной
степени,
возврат
идет
в
основ
ном
вследствие
поперечного
скольжения.
В
этом
случае
ползучесть
оказывается
неустановившейся:
скорость
ее
все
время
уменьша
ется
из-за
прогрессирующего,
хотя
и
замедляющегося
деформа
ционного
упрочнения
(число
аннигилирующих
дислокаций
меньше
числа
возникающих
при
деформации).
Затем
наступает
момент,
начиная
с
которого
число
переползающих
краевых
дислокаций
становится
достаточным
для
полного
возврата
(равенства
образу
ющихся
и
исчезающих
дислокаций).
С
э"[ОГо
момента
и
наблюда
ется
стадия
установившейся
ползучести.
Скорость
установившейся
ползучести
с
повышением
темпера
туры
испытания
быстро
растет
из-за
ускорения
диффузионного
процесса
переползания.
При
постоянном
напряжении
Vn,ycт
= K
o
exp(-Q/k1),
где ка
-
постоянная,
определяемая
уровнем
напряжений;
Q -
энергия
активации
ползучести,
также
зависящая
от
уровня
на
пряжения.
10·
291

Величина
Q
для
чистых
металлов
близка
к
энергии
активации
самодиффузии,
что
служит
основным
доказательством
контроля
скорости
установившейся
ползучести
процессом
переползания
дислокаций.
Зависимость
скорости
установившейся
ползучести
v
П.уст
от
напряжения
S
подчиняется
уравнению
v
=AS"
П.уст
'
(90)
где
коэффициент
n
при разных
температурах и
напряжениях
ме
няется
от
1
до
-4,
но
чаще
всего
близок
к
трем.
Большинство
физических
моделей
высокотемпературной
пол
зучести,
которые
исходят
из
того,
что
деформация
идет
путем
скольжения
и
переползания
дислокаций
и
что
в
условиях
устано
вившейся
ползучести
имеется
равновесие
скоростей
упрочнения
и
возврата,
при
водит к
n=3.
Если
принять,
что
скорость
возврата
при
нулевой
скорости
деформации
(dS;1
d't)1
dS/dt =
О
=
r,
а
коэффициент
деформационного
упрочнения
при
нулевой
ско
рости
возврата
(dS/d8)l
ds
/
dt
=O=
h,
то
скорость
установившейся
ползучести
d8/d't = V = r
/h
=
р ь
(L/l')v
,
П.уст.
п
т
(91)
где
рп
-
плотность
подвижных
дислокаций;
Ь
-
вектор
Бюргерса;
L -
средняя
длина
скольжения
между
двумя
препятствиями;
г
среднее
расстояние,
которое
проходит
дислокация
при
перепол
зании;
и
,.
-
скорость
переползания.
При
равномерном
распределении
дислокаций
их
плотность
р
-1/12,
(92)
где
1-
характерный
линейный
размер
конкретной
дислокацион
ной
структуры.
Поскольку
напряжение
вокруг
дислокации
убывает
пропорци
онально
расстоянию
от
нее,
зависимость
1
от
напряжения
должна
быть
(93)
292

в
уравнении
(91)
характерными
размерами
структуры
являют
сяLи/'.
При
низких
напряжениях
скорость
переползания
дислокаций
Vm-S.
Подставляя
выражение
(93)
в
(92),
получаем
р_
S2.
(94)
(95)
Поскольку
отношение
L/l'
в
уравнении
(91)
не
зависит
от
на
пряжения,
то
после
подстановки
формул
(95)
и
(94)
в
(91)
по
лучим
V _S3.
П.УСТ.
Деформация
при
высоких
температурах
и
низких
напряжениях
может
быть
не
связана
с
перемещением
дислокаций,
а
явиться
результатом
направленного
диффузионного
массопереноса.
При
отсутствии
внешних
напряжений
преимущественного
переноса
атомов
в
определенных
направлениях
не
происходит.
Но
если
металлический
кристалл
находится
в
поле
напряжений,
где
есть
растягивающие
и
сжимающие
компоненты,
то
концентрация
ва
кансий
оказывается
l;Iеодинаковой
на
растянутых
и
сжатых
по
верхностях,
что
вызывает
направленный
поток
вакансий
и
про
тивоположно
направленный
поток
атомов,
в
результате
дающий
макроскопическое
изменение
формы
кристалла.
Рассмотрим
кубическое
зерно
в
поликристалле
с
ребром
d,
находящееся
в
плосконапряженном
состоянии
(рис.
153).
Допус
тим,
что
внутри
зерна
нет
дислокаций,
и
поэтому
местами
стока
вакансий
могут
служить
только
его
границы.
На
горизонтальных
границах,
находящихся
под
действием
растягивающих
напряже
ний
S,
энергия
образования
вакансий
понижена
на
величину
Sb
3
,
где
Ь
3
-
объем
одного
атома,
а
на
вертикальных
(сжатых)
грани
цах
эта
энергия
повышена
на
ту
же
величину.
Действительно,
образование
вакансии
на
сжатой
-границе
равнозначно
выходу
на
нее
одного
атома
из
кристалла.
Если
атом
-
куб
с
ребром
Ь,
то
для
его
выхода
на
поверхность
границы
потребуется
затратить
работу
против
внешнего
напряжения
S,
равную
Sb
2
х
Ь
=
Sb
3.
В
результате
концентрация
вакансий
на растянутых границах
окажется
выше,
чем
на
сжатых
-
возникнет
градиент
концент
рации
вакансий,
который
приведет
к
их
направленному
переме
щению
от
горизонтальных
к
вертикальным
границам
вдоль
сплош-
293

Рис.
153.
Направления
движения
ва
кансий
и
атомов
(пунктир)
при
диффузионной
ползучести
ных
стрелок
на
рис.
153.
Встречный
поток
атомов
(вдоль
пунктирных
стре
лок
на
рис.
153)
вызовет
удлинение
и
соответствующее
сужение
зерна.
В
установившемся
режиме
число
вакансий,
перенесенных
за
1
с
через
поверхность
d
2
,
будет
Ф
=
-JеР,
где
по
закону
Фика
диффузионный
поток
J=
-Dgrad
С.
Здесь
D -
коэффициент
объемной
диффузии,
а
градиент
концентраций
grad
С
=
а.(С+
-
C-)/d,
где
о.
-
коэффициент·
пропорциональности,
а
С
+
и
С
- -
кон
центрации
вакансий
у
растянутых
и
сжатых
границ.
Тогда
Ф
=
Dd
2
Х
grad
С=
a.DCo/[exp
(Sb
3
/kT-ехр(-SЬ
3
/k1)]
и
Ф
=
20.
DCish(Sb3/kT),
(96)
где
Со
-
концентрация
вакансий
в
единице
объема,
связанная
с
равновесной
концентрацией
вакансий
по
=С
о
Ь
3
'
1 -
путь
диффу
зии.
Уравнение
(96)
можно
записать
и
с
использованием
коэффи
циента
самодиффузии
D'=
Dnо=DСоЪЗ:
Ф
=
(20.
Dd/b
3
)
sh (Sb
3
/kT).
Удлинение
кристалла
в
результате
выхода
на
его
растянутую
поверхность
еР
одного
атома
объемом
Ь
3
составит
Для
Ф
атомов
(вакансий),
перенесенных
за
1
с,
получим
ско
рость
диффузионной
ползучести
294

При
низких
напряжениях
гиперболический
синус
можно
при
нять
равным
его
аргументу,
и
тогда
(97)
Рассмотренная
модель
диффузионной
ползучести
носит
имя
ее
авторов
-
Набарро
и
Херринга.
В
последние
годы
она
была
усовершенствована
с
учетом
геометрии
зерен.
Однако
вид
урав
нения
(97)
остался
практически
неизменным
(в
него
только
вве
ден
коэффициент,
зависящий
от
формы
зерна).
Помимо
ползучести
Набарро
-
Херринга,
которая
учитывает
перенос
вещества
через
объем
кристаллов,
большое
значение
в
последние годы
придается
диффузионной
ползучести
Кобла,
ко
торый
предположил,
что
диффузионные
потоки
идут не
по
объе
му,
а
вдоль
границ
зерен.
Скорость
ползучести
по
Коблу
(98)
где
п
гр
-
коэффициент
зернограничной
диффузии;
(о
-
ширина
границы
зерна,
через
которую
проходит
диффузионный
поток;
в'
-
коэффициент,
зависящий
от
формы
зерна.
Направленный
массоперенос
по
объему
и
границам
зерен
про
ходит
одновременно,
а
их
вклад
в
деформацию
будет
различным
в
зависимости
от
температуры,
напряжения
и
размера
зерна,
что
следует
из
сопоставления
формул
(97)
и
(98).
Зернограничная
диффузия
идет
значительно
быстрее,
чем
объемная,
ее
энергия
активации
составляет
всего
0,35-0,7
от
энергии
активации
объемной
диффузии.
Поэтому
п
гр
не
так
силь
но
уменьшается
при
понижении
температуры,
как
коэффициент
объемной
диффузии,
и
ползучесть
Кобла
должна
вносить
тем
больший
относительный
вклад
в
общую
диффузионную
ползу
честь,
чем
ниже
температура.
Если
раньше
считали,
что
диффу
зионная
ползучесть
существенна
только
при
очень
высоких
тем
пературах
(выше
0,8-0,9
Т
п
)'
то
теперь
установлено
ее
большое
практическое
значение
(в
первую
очередь
ползучести
Кобла)
во
всем
температурном
интервале
высокотемпературной
ползучес
ти,
Т.е.
выше
0,4-0,6
Т
пл
'
Из
диаграммы
на
рис.
151,
а
видно,
что
температурно-силовые
области
проявления
диффузионной
и
вы
сокотемпературной
ползучести
с
возвратом
сильно
перекрыва
ются.
Вклад
диффузионной
ползучести
в
общее
удлинение
в
этих
295

условиях
тем
значительнее,
чем
выше
температура,
ниже
напря
жение
и
меньше
размер
зерна.
По
уравнениям
(97)
и
(98)
скорость
диффузионной
ползучес
ти
прямо
пропорциональна
напряжению.
Это
соответствует
нью
тоновскому
закону
вязкого
течения
и
предполагает,
что
направ
ленный
массоперенос
может
идти
при
любом
сколь
угодно
ма
лом
напряжении.
Теперь
экспериментально
установлено
наличие
у
каждого
материала
порогового
напряжения
So'
ниже
которого
диффузионная
ползучесть
не
развивается.
Величина
So
=(А/ф
exp(U/k1),
где
А
и
U -
константы.
Из
этого
уравнения
следует,
что
порого
вое
напряжение
уменьшается
с
повышением
температуры
и
ук
pyпHeHиeM
зерна.
В
области
высоких
гомологических
температур
So
становится
настолько
малым,
что
его
трудно
эксперименталь
но
зафиксировать.
Поскольку
наличие
порогового
напряжения
характерно
для
диффузионной
ползучести,
она
должна
подчиняться
не
ньюто
новскому
(когда
Vn-S) ,
а
бингамовскому
закону
течения
V
N
= K(S -
So).
(99)
Следовательно,
в
уравнениях
(97)
и
(98),
сохраняющих
свою
силу,
следует
действующее
напряжение
S
заменить на
разность
между
ним
и
пороговым
напряжение'м
(S -
So).
Коэффициент
К
в
уравнении
(99)
заменяет
все
остальные
члены
уравнений
(97)
и
(98).
Из
приведенного
выше
анализа
скорости
ползучести
следует,
что
основными
факторами,
определяющими
механизм
деформа
ции
и
величину
V
n
'
являются
температура
т,
напряжение
S
или
t(r)
и
размер
зерна
d.
Поэтому
в
последние
годы
получили
рас
пространение
предложенные
Эшби
карты
механизмов
деформа
ции,
которые
чаще
всего
строят
в
координатах
"[-
Т
при
d = const.
Для
удобства
сравнения
металлов
с
разными
температурами
плав
ления
и
модулями
упругости
используют
координаты
't/G -
Т/Т
nл
(см.
рис.
151,
б).
При
заданных
значениях
S
и
Т
ползучесть
может
осуществ
ляться
за
счет
действия
нескольких
механизмов
деформации.
Гра
ницы
соседних
областей
на
рис.
151,
б
-
это
геометрическое
ме
сто
точек
температур
и
напряжений,
обеспечивающих
одинако
вый
вклад
двух
конкурирующих
механизмов
деформации
в
об-
296

щую
ползучесть,
а
точки
встречи
трех
областей
соответствуют
равенству
вкладов
трех
механизмов
деформации.
Положение
гра
ниц
областей
рассчитывают
по
уравнениям
скорости
различных
видов
ползучести.
Карты
механизмов
деформации
полезны
для
наглядного
изображения
смены
доминирующих
механизмов
пол
зучести
при
изменении
условий
нагружения,
а
также
размера
зерна
в
материале.
2.
Испытания
на
ползучесть
Для
оценки
поведения
металлов
и
сплавов
в
условиях
ползуче
сти
проводят
различные
испытания.
Обычно
в
этих
испытаниях
реализуются
условия
высокотемпературной
и
диффузионной
пол
зучести,
так
как
их
ведут
при
температурах
выше
0,4-0,6
Т
пл
'
соответствующих
рабочим
температурам
жаропрочных
металли
ческих
материалов.
Основной
целью
стандартных
испытаний
на
ползучесть
при
растяжении
(ГОСТ
3248 - 81)
является
определение
предела
пол
зучести
материала.
Предел
ползучести
-
это
условное
растягива
ющее
напряжение,
при
котором
скорость
или
деформация
пол
зучести
за
определенное
время
достигают
заданной
величины.
В
случае
высокотемпературной
ползучести
имеется
в
виду
скорость
на
установившейся
стадии.
Если
допуск
дается
по
скорости
ползучести,
то
предел
ползу
чести
обозначается
буквой
cr
с
двумя
индексами
-
нижний
соот
ветствует
заданной
V
n
'
%jч,
а
верхний
-
температуре
испыта-
ния,
ос.
Например,
a:.~~~
-
это
предел
ползучести
при
11000
С
и
v
n
=1 • 10-4
%jч.
Если
задается
относительное
удлинение
и
время
его
достижения,
то
в
обозначение
предела
ползучести
вводят
три
индекса:
один
верхний
соответствует
температуре
испытания,
а
два
нижних
-
деформации
и
времени.
Например,
cr~J~ooo
-
пре
дел
ползучести
при
8000
С,
когда
8=
1 %
достигается
за
1000
ч.
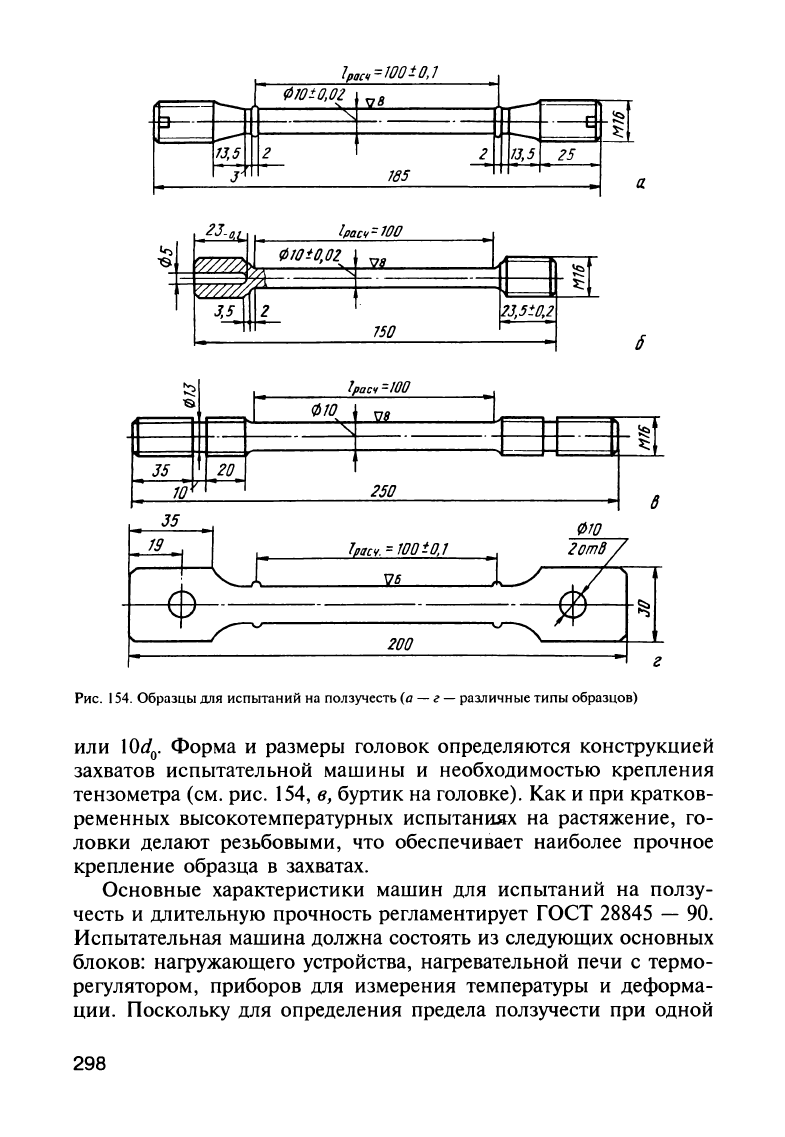
Испытания
проводят
на
образцах
с
круглым или
прямоуголь
ным
сечением
рабочей
части
(рис.
154).
Цилиндрический
образец
имеет
диаметр
10
и
расчетную
длину
100
или
200
мм,
плоский
-
ширину
15
и
расчетную
длину
100
мм.
Допускается
использование
других
образцов
с
диаметром
do~5
мм
и
расчетной
длиной
'о
=
5d
o
297
pacQ-
- ,
1
-!Оо,+{},
7
~1O!o,o!
v8
~:
.--tJ
~I
Ч5
2
2
Ц5
25
J
785
а
tf
~
'рос.=/ОО
"&
I/J!о'
1
fЗ8
1-
-
"'
1
.--t
-
~!
r---
J5
20,
10
250,
6
-f----1f-t--,1--
----
----
----
---hI'+---I-~
г
Рис.
154.
Образuы
ДЛЯ
испытаний
на
ползучесть
(о
-
г
-
различные
типы
образuов)
или
10d
o
.
Форма
и
размеры
головок
определяются
конструкцией
захватов
испытательной
машины
и
необходимостью
крепления
тензометра
(см.
рис.
154,
в,
буртик
на
головке).
Как
и
при
кратков
ременных
высокотемпературных
испытаниях
на
растяжение,
го
ловки
делают
резьбовыми,
что
обеспечивает
наиболее
прочное
крепление
образца
в
захватах.
Основные
характеристики
машин
для
испытаний
на
ползу
честь
и
длительную
прочность
регламентирует
ГОСТ
28845
-
90.
Испытательная
машина
должна
состоять из
следующих
основных
блоков:
нагружающего
устройства,
нагревательной
печи
с
термо
регулятором,
приборов
для
измерения
температуры
и
деформа
ции.
Поскольку
для
определения
предела
ползучести
при
одной
298
температуре
требуется
несколько
образцов
и
испытания
продол
жаются
в
течение
сотен
и
тысяч
часов,
нагружающие
устройства
конструируют
таким
образом,
чтобы
на
одной
установке
можно
было
одновременно
испытывать
по
несколько
образцов.
Нагрузка
на образец
обычно
подается
через
рычажную
систему,
либо
не
посредственно
(подвешиванием
груза).
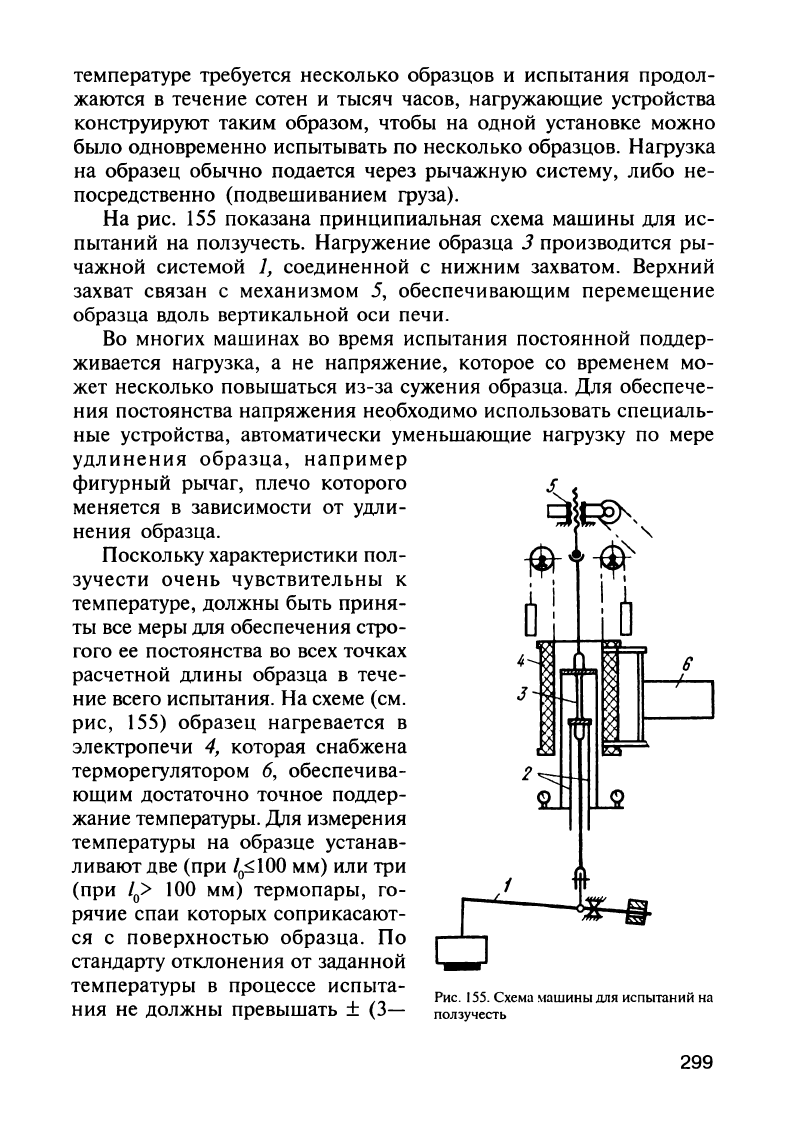
На
рис.
155
показана
принципиальная
схема
машины
для
ис
пытаний
на
ползучесть.
Нагружение
образца
3
производится
ры
чажной
системой
1,
соединенной
с
нижним
захватом.
Верхний
захват
связан
с
механизмом
5,
обеспечивающим
перемещение
образца
вдоль
вертикальной
оси
печи.
Во
многих
машинах
во
время
испытания
постоянной
поддер
живается
нагрузка,
а
не
напряжение,
которое
со
временем
мо
жет
несколько
повышаться
из-за
сужения
образца.
Для
обеспече
ния
постоянства
напряжения
необходимо
использовать
специаль
ные
устройства,
автоматически
уменьшающие
нагрузку
по
мере
удлинения
образца,
например
фигурный
рычаг,
плечо
которого
меняется
в
зависимости
от
удли
HeHия
образца.
Поскольку
характеристики
пол
зучести
очень
чувствительны
к
температуре,
должны
быть
приня
ты
все
меры
для
обеспечения
стро
гого
ее
постоянства
во
всех
точках
расчетной
длины
образца
в
тече
ние
всего
испытания.
На
схеме
(см.
рис,
155)
образец
нагревается
в
электропечи
4,
которая
снабжена
терморегулятором
6,
обеспечива
ющим
достаточно
точное
поддер
жание
температуры.
Для
измерения
температуры
на
образце
устанав
ливают
две
(при
'o~100
мм)
или
три
(при
/0>
100
мм)
термопары,
го
рячие
спаи
которых
соприкасают
ся
с
поверхностью
образца.
По
стандарту
отклонения
от
заданной
температуры
в
процессе
испыта
ния
не
должны
превышать
±
(3-
J
2
f
Рис.
155.
Схема
машины
для
испытаний
на
ползучесть
299
