Золотаревский В.С. Механические свойства металлов
Подождите немного. Документ загружается.


вов
до
установления
норм
на
образцы
с
У-образным
концентра
тором.
Образцы
с
надрезом
и
трещиной
предназначены
для
ис
пытания
материалов,
работающих
в
особо
ответственных
конст
рукциях,
где
сопротивление
развитию
трещины
имеет
первосте
пенное
значение.
При
испытании
образцов
с
L=55
мм
расстояние
между
опора
ми
должно
быть
40
мм.
Изгибающий нож
имеет
сечение
в
виде
треугольника
с
углом
при
вершине
300
и
радиусом
закругления
2
мм.
Испытания
на
изгиб
проводят на
маятниковых
копрах
с
пре
дельной
энергией,
не
превышающей
300
Дж*.
Копры
должны
соответствовать
требованиям
ГОСТ
10708-82.
Схема
испытания
приведена
на
рис.
132.
Образец
кладут
гори
зонтально
в
специальный
шаблон,
обеспечивающий
установку
надреза
строго
в
середине
пролета
между
опорами.
Удар
наносят
со
стороны,
противоположной
надрезу,
в
плоскости,
перпенди
кулярной
продольной
оси
образца.
Маятник
копра
закрепляется
в
исходном
верхнем
положении.
По
шкале
фиксируется
угол
подъема
маятника
а..
Затем
крепящую
защелку
вынимают,
маятник
свободно
пада
ет
под
собственной
тяжестью,
ударяет
по
образцу,
изгибает
и
разрушает
его,
поднимаясь
относительно вертикальной
оси
коп
ра
на
угол
/3.
Этот
угол
тем
меньше,
чем
большая
работа
К
(при
испытании
стандартных
образцов
обозначается
КU,
KV
или
КТ
в
зависимости
от
геометрии
надреза)
затрачена
маятником
на
де
формацию
и
разрушение
образца.
Скорость
копра
и
к
,
м/с,
в
мо
мент
удара
по
образцу
зависит
от
высоты
подъема
Н
(см.
рис.
132):
и
к
=
(2gН)
1/2,
где
g -
ускорение
свободного
падения.
Величина
работы
деформации
и
разрушения
определяется
раз
ностью
потенциальных
энергий
маятника
в
начальный
(после
подъема
на
угол
а.)
И
конечный
(после
взлета
на
угол
/3)
момен
ты
испытания:
К=
Р(Н
- h),
где
Р
-
вес
маятника;
Н
и
h -
высоты
подъема
и
взлета
маятни
ка
(см.
рис.
132).
• 1
Дж,.,
0,1
КГС·М.
250

Если
длина
маятника
L,
то
h = L
(1
- cos
~),
Н=
L
(1
- cos
а)
и,
следовательно,
к
= PL(cos
~
- cos
а).
Эта
формула
и
служит
для
расчета
работы
К
по
измеренным
углам
а
и
~
(Р
и
L
постоянны
для
данного
копра).
Шкала
копра
может
быть
проградуирована
в
единицах
работы,
если
угол
подъема
маятника
а
фиксирован.
Часть
энергии
удара
затрачивается
на
сотрясение
копра
и
фун
дамента,
преодоление
сопротивления
воздуха,
на
трение
в
под
шипниках
и
в
измерительном
устройстве,
на
смятие
образца
на
опорах
и
под
ножом,
на
сообщение
энергии
обломкам
образца
и
на
упругую
деформацию
штанги
маятника.
На
копрах,
применяемых
при
обычных
испытаниях
металлов,
большинство
этих
потерь
не
поддается
учету,
в
результате
полу
чаемые
значения
К
оказываются
завышенными
на
несколько
про
центов.
Особенно
велики
потери
энергии
при
несовпадении
оси
удара
и
середины
надреза
на
образце.
Поэтому
величины
ударной
вязкости,
определенные
на
различных
копрах,
могут
отличаться
друг
от
друга
на
10-30%.
Точность
определения
работы излома
тем
выше,
чем
меньше
превышение
запаса
работы
маятника
над
работой
деформации
и
разрушения
образца;
нужно
стремиться,
чтобы
угол
~
после
разрушения
образца
был
небольшим.
Зная
полную
работу
деформа
ции
и
разрушения,
К,
можно
рас
считать
основную
характеристику,
получаемую
в
результате
рассмат
риваемых
испытаний
-
ударную
вязкость:
КС
= KjF,
(74)
где
F -
площадь
поперечного
се
чения
образца
в
месте
надреза
до
испытания.
Рис.
132.
Схема
ударного
испытания
на
изгиб на
маятниковом
копре
251

Стющартная
размерность
ударной
вязкости
Дж/см
2
или
КГС'
м/см
2
*.
В
зависимости
от
вида
концентратора
в
образце
в
обозначение
ударной
вязкости
вводится
третий
индекс
(и,
V
или
1).
Напри
мер,
KCV
-
ударная
вязкость,
определенная
на
образце
с
у
образным
концентратором
при
комнатной
температуре.
Допуска
ется
обозначение
ударной
вязкости
аи,
aV,
ат.
Ударные
испытания,
как
и
статические,
можно
проводить
при
отрицательных
и
повышенных
температурах.
Методика
этих
ис
пытаний
также
регламентирована
ГОСТ
9454-78.
Динамический
изгиб
при
отрицательных
температурах
производят
с
использова
нием
тех
же
образцов, что
и
при
комнатной.
Образец
вьщержива
ют
в
жидком
хладагенте
не
менее
15
мин
при
температуре
на
2-
6
ос
ниже
заданной,
затем
вынимают
из
ванны,
устанавливают
на
копер
и
немедленно
испытывают.
Аналогичная
методика
используется
при
высокотемператур
ных
испытаниях.
Предварительный
нагрев
образцов
рекоменду
ется
вести
в
муфельных
печах,
при
необходимости
в
нейтральной
атмосфере,
перегревая
образец
относительно
заданной
темпера
туры
на
3-50
ос
в
зависимости
от
ее
абсолютной
величины.
При
этом
время
установки
образца
с
момента
выемки
из
печи
до
уда
ра
маятника
должно
быть
не
больше
3-5
с.
Для
обозначения
ударной
вязкости
при
пониженной
или
по
вышенной
температурах
используется
цифровой
индекс,
соот
ветствующий
температуре
испытания.
Например,
КСТ60
-
удар
ная
вязкость,
определенная
на
образце
с
Т-образным
концент
ратором
при
-60
ОС.
В
ГОСТ
9454-78
рекомендуется
при
обозна
чении
ударной
вязкости
указывать
также
максимальную
энергию
удара
маятника,
Дж,
глубину
концентратора,
мм,
в
испытанном
образце
и
его
ширину,
мм.
Например,
KC[J+JOO
150/3/7,5 -
удар
ная
вязкость,
определенная
на
образце
с
U-образным
концент
ратором
при
100
ос
на
копре
с
максимальной
энергией
удара
ма
ятника
150
Дж
при
глубине
концентратора
3
мм
и
ширине
образ
ца
7,5
мм.
Если
используется
копер
с
максимальной
энергией
удара
маятника
300
Дж
и
образец
шириной
1
О
мм
с
глубиной
концен
тратора
2
мм,
то
эти
данные
в
обозначение
ударной
вязкости не
вводятся
(пишется
просто
KC[J+JOO).
В
массовых
динамических
испытаниях
на
изгиб
образцов
с
над
резом
ударная
вязкость
-
единственная
выходная
характеристи-
* 1
Дж/см
2
",
0,1
КГС'
м/см
2
.
252

ка
испытания.
Диаграмма
деформации
обычно
не
записывается,
так
как
это
сопряжено
со
значительными
экспериментальными
трудностями.
Общее
время
испытания
измеряется
долями
секун
ды,
поэтому
для
фиксации
зависимости
нагрузки
от
деформации
требуются
малоинерционные
чувствительные
датчики
и
быстро
действующий
прибор
для
записи
диаграмм.
Обычно
используют
пьезокварцевые
динамометры
и
шлейфовые
осциллографы.
Характеристики
пластичности
-
стрелу
изгиба
и
угол загиба
-
легко
определить,
сложив
две
половины
разрушенного
образ
ца
точно
так
же,
как
при
испытаниях
на
статический
изгиб.
Ударная
вязкость
-
это
сложная,
комплексная
характеристи
ка,
зависящая
от
совокупности
прочностных
И
пластических
свойств
материала.
Работа,
затрачиваемая
на
пластическую
де
формацию
и
разрушение,
определяется
площадью
под
диаграм
мой
динамического
изгиба.
Ее
величина,
следовательно,
будет
тем
больше,
чем
выше
пластичность
и
уровень
напряжений
тече
ния
на
всем
протяжении
испытания.
При
ударных
испытаниях
на
изгиб
образцов
с
надрезом
на
пряжения
и
пластическая
деформация
концентрируются
в
огра
ниченной
части
объема
образца
вокруг
надреза.
Именно
здесь
поглощается
практически
вся
рабо
та
удара.
На
рис.
133,
а
показаны
границы
области
распространения
пластической
деформации
при
раз
ной
глубине
надреза.
Видно,
что
ширина
этой
области
соизмерима
с
высотой
сечения
образца
и
увели
чивается
по
мере
уменьшения
глу
бины
надреза.
На
рис.
133,
б
дана
схема
распредедения
продольных
нормальных
напряжений
SI
в
сече
нии
надреза.
В
районе
вершины
над
реза,
помимо
SI'
дейстнуют
попе
речные
нормальные напряжения
S2
и
Sз
(Sз
не
показано
на
рис.
133,
б,
так
как
оно
перпендикулярно
плос
кости
чертежа).
Их
появление
выз
вано
торможением
поперечной
де
формации
объемами
образца,
при
мыкающими
с
двух
сторон
к
надре-
(J
$,
Sz
tf
Рис.
133.
Области
(1,
2,
3)
раСПРОС1р3не
ния
пластической
деформации
при
раз
ной
глубине
надреза
(а)
и
схема
рас
пределения
продольных
напряжений
S,
в
сечении
надреза
(6)
при
ударном
из
гибе
253
зу.
Чем
глубже
и
острее
надрез
и
больше
ширина
сечения,
тем
больше
величина
всех
трех
нормальных
напряжений
в
точке
М
и
меньше
работа
К.
Повышение
ударной
вязкости
материала
часто
сопровождает
ся
и
увеличением
деформируемого
объема
в
области
надреза.
Возникновение схемы
объемного
растяжения,
концентрация
напряжений
у надреза,
а
также
рост
предела
текучести
в
резуль
тате
ускорения
деформации
при
мало
меняющейся
хрупкой
проч
ности
(см.
схему
Иоффе
на
рис.
73)
создают
наиболее
благоприят
ные
условия
для
хрупкого
разрушения.
Количественно
величину
деформируемого
объема
при
удар
ном
испытании
определить
трудно.
Поэтому
при
расчете
ударной
вязкости
полную
работу
деформации
разрушения
относят
не
к
объему,
а
к
площади
Fпоперечного
сечения
в
надрезе,
что,
строго
говоря,
не
имеет
физического
смысла.
При
испытании
стандарт
ных
образцов
величина
F
постоянна
и,
следовательно,
ударная
вязкость
прямо
пропорциональна
полной
работе
К.
Поскольку
в
разных
материалах
или
при
различных
температурах
испытания
пластически
деформируются
различные
объемы,
то
при
одина
ковых
значениях
К
получаются
разные
величины
удельной
рабо
ты
(в
расчете
на
единицу
объема).
Ударная
же
вязкость
в
этом
случае
оказывается
одинаковой.
Таким
образом,
характеристика
ударной
вязкости
КС
является
условной,
и
это
необходимо
учитывать
при
сопоставлении
раз
ных
материалов.
Как
уже
отмечалось,
одной
из
важнейших
задач
ударных
ис
пытаний
является
оценка
склонности
к
хрупкому
разрушению.
Эта
задача
решается
построением
температурной
зависимости
ударной
вязкости
и
определением
/(1:
_-----7
,-
Рис.
134.
Типы
температурных
зависи
мостей
ударной
вязкости
254
температурыхрупко-вязкогоперехо
да.
Возможны
три
типа
кривых
удар
ная
вязкость-температура
(рис.
134).
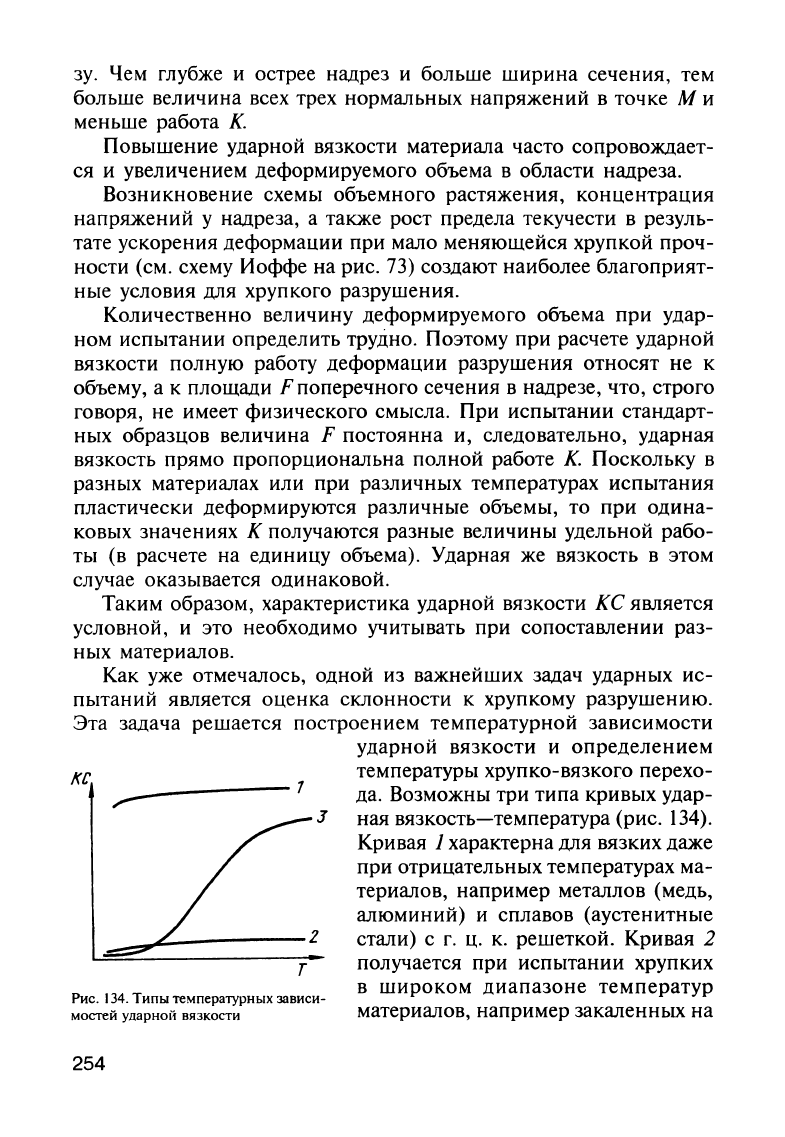
Кривая
1
характерна
для вязких
даже
при
отрицательных
температурах
ма
териалов,
например
металлов
(медь,
алюминий)
и
сплавов
(аустенитные
стали)
с
г.
ц.
к.
решеткой.
Кривая
2
получается
при
испытании
хрупких
в
широком
диапазоне
температур
материалов,
например
закаленных
на

мартенсит
сталей.
Наконец,
кривая
3
характеризуется
темпера
турным
интервалом
хрупко-вязкого
перехода,
по
ней
можно
оце
нить
Т
.
Такой
тип
кривых
КС-
Т
типичен
для
металлов
с
о.
ц.
к.
хр
И
г.
п.
решетками,
многих
сталей
с
феррито-перлитной
структу-
рой.
Зная
Т
и
рабочую
температуру
Т
испытуемого
материала,
~
р
можно
оценить
его
температурный
запас
вязкости:
Х
=
(Т
-
Т
)/
Т.
р
хр
р
Чем
больше
Х,
тем
меньше
опасность
хрупкого
разрушения.
Поскольку
хрупкий
и
вязкий
характер
разрушения
при
удар
ном
изгибе
четко
различается
по
виду
излома
(блестящий
«крис
таллический»
или
матовый,
волокнистый),
т.
р
можно
определять
по
структуре
излома.
За
т.
р
принимают
температуру,
при
которой
в
изломе
появляются
первые
участки
хрупкого
разрушения
или
он
становится
полностью
хрупким.
Возможна
также
оценка
Т
хр
как
температуры,
соответствующей
равным
долям
хрупких
и
вяз
ких
участков
разрушения
в
изломе.
Динамические
испытания
на
изгиб
надрезанных
образцов
яв
ляются
самыми
жесткими
среди
стандартных
испытаний.
Для
оцен
ки
температуры
хрупко-вязкого
перехода
эти
испытания
приме
няют
в
тех случаях,
когда
статические
испытания
не
позволяют
выявить
эту
температуру
(образцы
пластичны
вплоть
до
глубоких
отрицательных
температур).
Полезны
они
и
для
оценки
этой
тем
пературы
у
материалов,
которые
могут
подвергаться
ударным
нагружениям
при
эксплуатации.
Наконец,
ударные
испытания
часто
используют
для
определения
«максимальной»
т.
р
•
Действи
тельно,
переход
в
хрупкое
состояние
в
условиях
динамического
нагружения
происходит
при
более
высоких
температурах,
чем при
статических
испытаниях.
Поэтому
оценка
склонности
к
хрупкому
разрушению
в
наиболее
жестких
условиях
представляет
самосто
ятельный
интерес.
Определение
температуры
хрупко-вязкого
перехода
по
темпе
ратурной
зависимости
ударной
вязкости
имеет
ряд
принципи
альных
недостатков.
Главный
из
них
заключается
в
том,
что
удар
ная
вязкость
характеризует
суммарное
сопротивление
образца
пластической
деформации
и
разрушению.
Определяя
же
т.
р
'
мы
стремимся
оценить
только
сопротивление
разрушению,
т. е.
рас
пространению
трещины.
Для
того
чтобы
вьщелить
эту
составляю
щую
полной
работы
Кл'
используют
следующий
метод.
На
копре
с
255
постепенно
увеличивающимся
запасом
работы
маятника
(увели
чением
угла
а,
рис.
132)
испытывают
несколько
образцов
и
стро
ят
зависимость
угла
загиба
от
полной
работы
Кл
(рис.
135).
Если
образцы
(при
малых
углах
подъема
маятника)
не
разрушаются,
то
величину
КЛ
принимают
равноЙ
запасу
работы
маятника
РН
=
РЦ1
- cos
а).
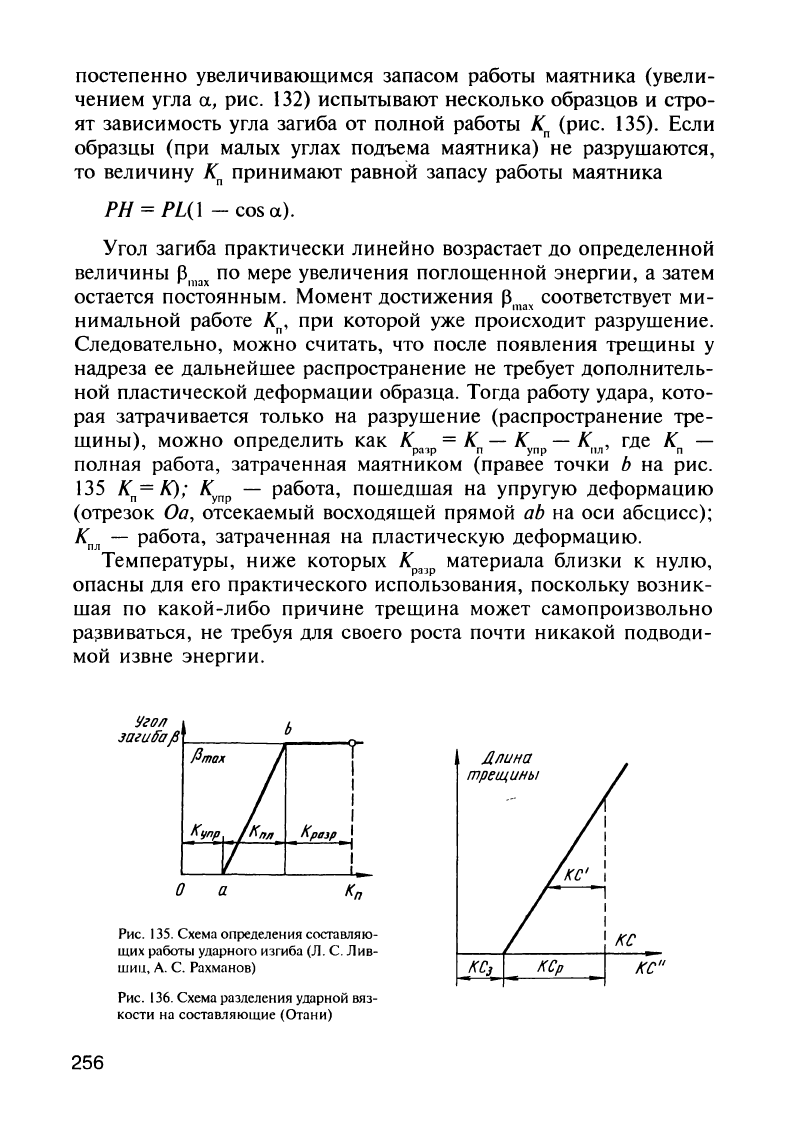
Угол
загиба
практически
линейно
возрастает
до
определенной
величины
Р
шох
по
мере
увеличения
поглощенной
энергии,
а
затем
остается
постоянным.
Момент
достижения
Р
l11аХ
соответствует
ми
нимальной
работе
Кл'
при
которой
уже
происходит
разрушение.
Следовательно,
можно
считать,
что
после
появления
трещины
у
надреза
ее
дальнейшее
распространение
не требует
дополнитель
ной
пластической
деформации
образца.
Тогда
работу
удара,
кото
рая
затрачивается
только на
разрушение
(распространение
тре
щины),
можно
определить
как
К
=
К
- К - К ,
где
К
-
ра1Р
n
упр
пл
n
полная
работа,
затраченная
маятником
(правее
точки
Ь
на
рис.
135
К
=
К);
к
-
работа,
пошедшая
на
упругую
деформацию
л
упр
(отрезок
00,
отсекаемый
восходящей
прямой
аЬ
на
оси
абсцисс);
К
пл
-
работа,
затраченная
на
пластическую
деформацию.
Температуры,
ниже
которых
К
разр
материала
близки
к
нулю,
опасны
для
его
практического
использования,
поскольку
возник
шая
по
какой-либо
причине
трещина
может
самопроизвольно
ра;звиваться,
не
требуя
для
своего
роста
почти
никакой
подводи
мой
извне
энергии.
256
!lгUIl
Ь
ЗОгtfОО
J11----::-------.---r
о
а
Рис.
135.
Схема
определения
составляю
щих
работы
ударного
изгиба
(Л.
С.
Лив
шиц,
А.
С.
Рахманов)
Рис.
136.
Схема
разделения
ударной
вяз
кости
на
составляющие
(Отани)
ДIlLJна
треЩLJНЫ
/(С;
/(С"

Полную
работу
К
(или
ударную
вязкость
КС)
можно
разделить
на
составляющие,
определяющие
работу
зарождения
и
работу
распространения
трещины.
Для
этого
при
заданной
температуре
испытывают
несколько
образцов
при
двукратном
приложении
ударной
нагрузки.
Первый
удар
наносят
маятником,
поднятым
на
заведомо
меньший
угол,
чем
необходимо
для
полного
разру
шения.
При
этом
вблизи
надреза
зарождается
трещина.
Затем
на
носят
разрушающий
образеu
второй
удар,
подняв
маятник
на
высоту,
используемую
при
стандартных
испытаниях,
фиксируют
величину
ударной
вязкости
КС'
и
измеряют
глубину
полученной
при первом
ударе
грещины
[,
например,
с
помощью
10%-ного
щелочного
раствора
двухлористой
меди,
который
окрашивает
трещину
ИЗ-З<l
осаждения
на
ее
поверхности
слоя
меди.
Исходя
из
того,
что
при
втором
ударе
работа,
пропорциональная
КС',
рас
ходуется
только
на
распространение
трещины,
строят
диаграмму
в
координатах
длина
трещины
[-КС"
(КС"=
КС
-
КС'),
где
КС
-
стандартная
ударная
вязкость,
определенная
в
результате
од
нократного
удара
(рис.
136).
Точка
пересечения
прямой
'-КС"
с
осью
абсцисс
дает
величину
КС]
пропорциональную
работе
за
рождения
трещины,
а
разность
КС
-
КС]
=
КС
р
-
долю
ударной
вязкости,
приходящуюся
на
распространение
трещины.
Показано,
что
работа
распространения
трещины
не
меняется
при
изменении
остроты
надреза
и
становится
ничтожно
малой
при
температурах,
более
высоких,
чем
обычная
Т
хр
'
когда
удар
ная
вязкость
еще
достаточно
высока.
Следовательно,
большая
ве
личина
КС
не
гарантирует
вязкого
разрушения.
В
реальных
усло
виях
материал
может
оказаться
хрупким,
так
как
энергия
рас
пространения
в
нем
трещины
близка
к
нулю.
Разделить
ударную
вязкость
на
две
составляющие
-
КС
и
КС
]
Р
-
можно,
построив
зависимость
КС
от
радиуса
кривизны
надре-
за
r.
Действие
очень
острого надреза
аналогично
действию
заро
дышевой
трещины.
Поэтому
при
значениях
радиуса
закругления
надреза,
меньших
какого-то
критического,
величина
ударной
вяз
кости
будет
постоянна.
В
координатах
KC--vr
эта
зависимость
бу
дет
иметь
вид,
схематично
показанный
на
рис.
137.
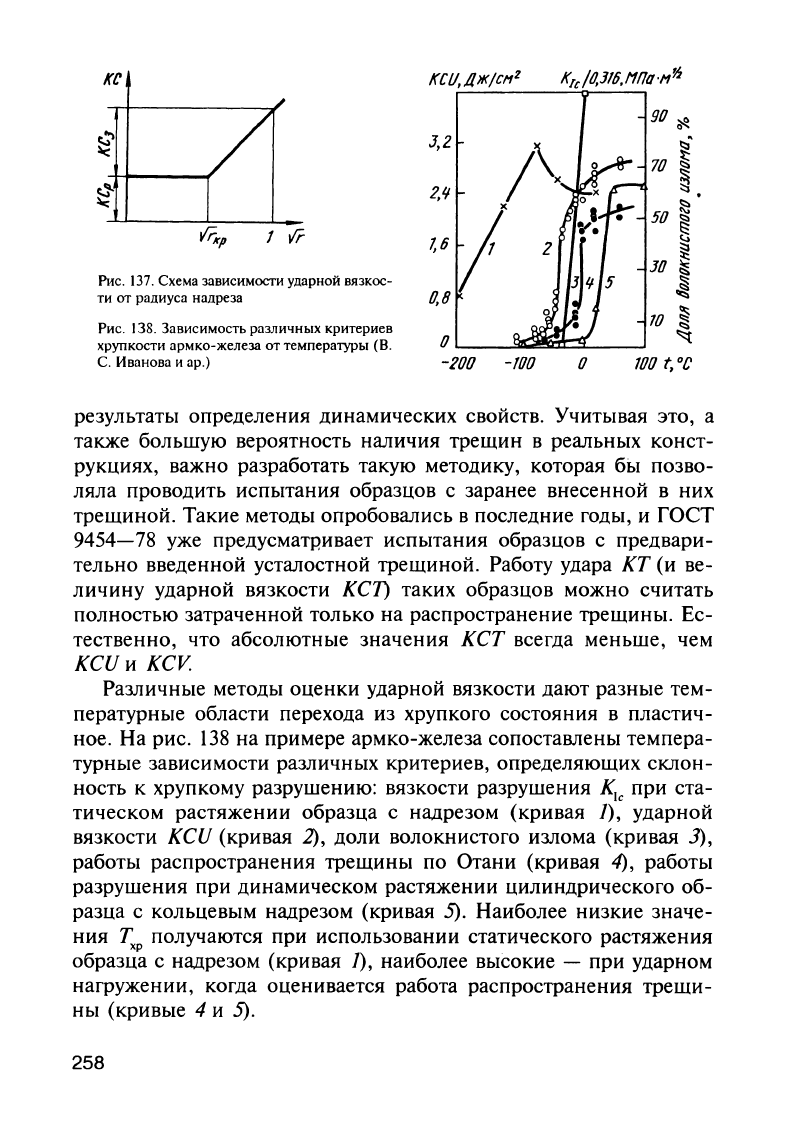
Постоянный
уровень
значений
ударной
вязкости
при
r < r
соответствует
КС
,
КР
..
У.
пропорциональной
работе
распространения
трещины,
а
КСз=КС
-
КС.
р
Описанные
выше
нестандартные
методы
ударных
испытаний
на
изгиб
наглядно
демонстрируют
сильное
влияние
трещин
на
9
~
3755
257
Kt
Рис.
137.
Схема
зависимости
ударной
вязкос
ти от
радиуса
надреза
Рис.
138.
3ависимость
различных
критериев
хрупкости
армко-железа
от
температуры
(В.
С.
Иванова
и
ар.)
КС//,ДЖ/С,.,Z
результаты
определения
динамических
свойств.
Учитывая
это,
а
также
большую
вероятность
наличия
трещин
в
реальных
конст
рукциях,
важно
разработать
такую
методику,
которая
БыI
позво
ляла
проводить
испытания
образцов
с
заранее
внесенной
в
них
трещиной.
Такие
методы
опробовались
В
последние
годы,
и
ГОСТ
9454-78
уже
предусмаТр'ивает
испытания
образцов
с
предвари
тельно
введенной
усталостной
трещиной.
Работу
удара
КТ
(и
ве
личину
ударной
вязкости
КС1)
таких
образцов
можно
считать
полностью
затраченной
только
на
распространение
трещины.
Ес
тественно,
что
абсолютные
значения
КСТ
всегда
меньше,
чем
КСUи
KCV.
Различные
методы оценки
ударной
вязкости
дают
разные
тем
пературные
области
перехода
из
хрупкого
состояния
в
пластич
ное.
На
рис.
138
на
примере
арм
ко-железа
сопоставлены
темпера
турные
зависимости
различных
критериев,
определяющих
склон
ность
к
хрупкому
разрушению:
вязкости
разрушения
K
1c
при
ста
тическом
растяжении
образца
с
надрезом
(кривая
J),
ударной
вязкости
кси
(кривая
2),
доли
волокнистого
излома
(кривая
3),
работы
распространения
трещины
по
Отани
(кривая
4),
работы
разрушения
при
динамическом
растяжении
цилиндрического
об
разца
с
кольцевым
надрезом
(кривая
5).
Наиболее
низкие
значе
ния
т.
р
получаются
при
использовании
статического
растяжения
образца
с
надрезом
(кривая
1),
наиболее
высокие
-
при
ударном
нагружении,
когда
оценивается
работа
распространения
трещи
ны
(кривые
4
и
5).
258
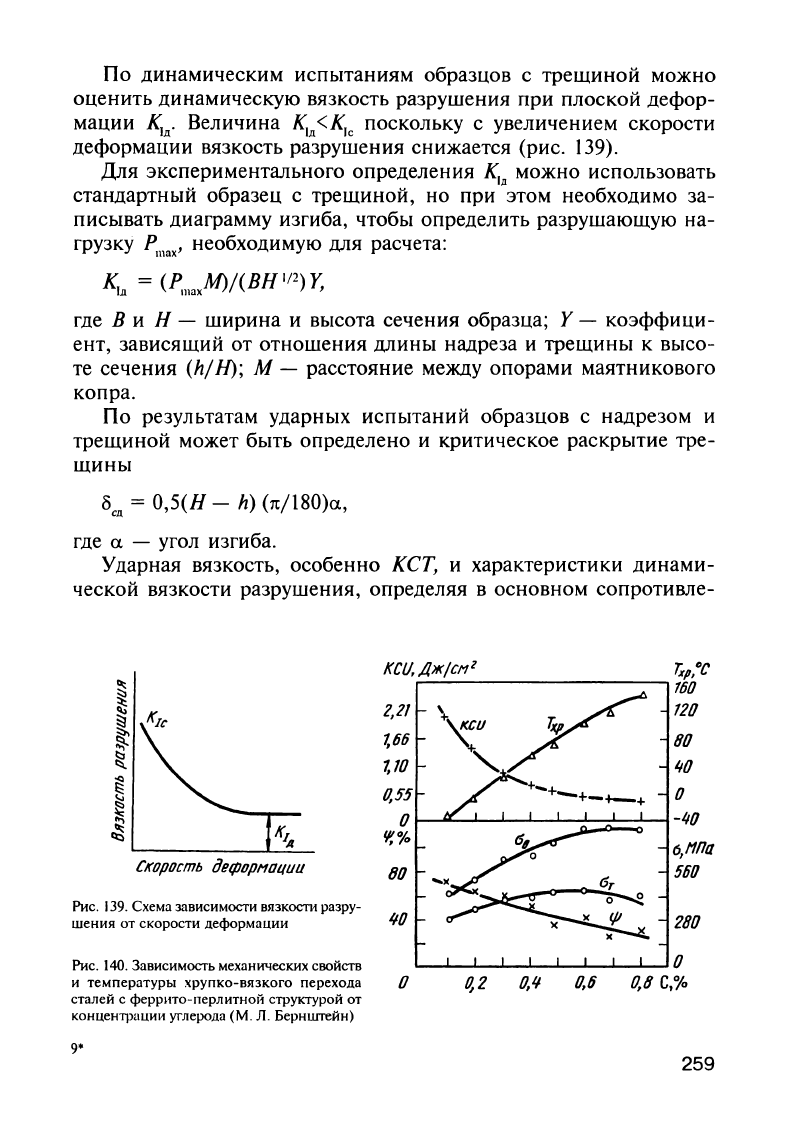
По
динамическим
испытаниям
образцов
с
трещиной
можно
оценить
динамическую
вязкость
разрушения
при
плоской
дефор
мации
к.,д'
Величина
KIд
<K
1c
поскольку
с
увеличением
скорости
деформации
вязкость
разрушения
снижается
(рис.
139).
Для
экспериментального
определения
к.,д
можно
использовать
стандартный
образец
с
трещиной,
но
при
этом
необходимо
за
писывать
диаграмму
изгиба,
чтобы
определить
разрушающую
на
грузку
Р.11.Х'
необходимую
для
расчета:
к
=
(Р
М)/(ВН
1/2)
у.
Iд
шах
'
где
В
и
Н
-
ширина
и
высота
сечения
образца;
У
-
коэффици
ент,
зависящий
от
отношения
длины
надреза
и
трещины
к
высо
те
сечения
(h/
Н);
м
-
расстояние
между
опорами
маятникового
копра.
По
результатам
ударных
испытаний
образцов
с
надрезом
и
трещиной
может
быть
определено
и
критическое
раскрытие
тре
щины
Оед
=
0,5(Н
- h)
(п/180)а,
где
а
-
угол
изгиба.
Ударная
вязкость,
особенно
кст,
и
характеристики
динами
ческой
вязкости
разрушения,
определяя
в
основном
сопротивле-
~
~
~
~
~
~
~
~
~
KJД
Скорость
tJеФОРl10ЦUU
Рис.
139.
Схема
зависимости
ВЯЗКОСТИ
разру
шения
от
скорости
деформации
Рис.
140.
Зависимость
механических
свойств
и
температуры
хрупко-вязкого
перехода
сталей
с
феррито-перлитной
структурой
от
концентрации
углерода
(м.
Л.
Бернштейн)
9'
кcu.ДЖ/СI1
2
7;р,ОС
~/
150
2,21
120
1,55
ВО
1,10
"О
0,55
-+-+-+-+
О
О
-110
v.~
6,I1ПIl
ВО
550
40
280
О
О
~2
0,'1
0,5
о,в
С,%
259
