Зоценко Н.Л. Инженерная геология. Механика грунтов, основания и фундаменты

Подождите немного. Документ загружается.

160

T γηττ

, (6.15)

де T

=η/G

– час релаксації.

При постійній деформації γ=const рішення (6.15) при початковій умові t=0 τ=τ

приво-

дить до рівняння релаксації

T/t

−

ττ

. (6.16)

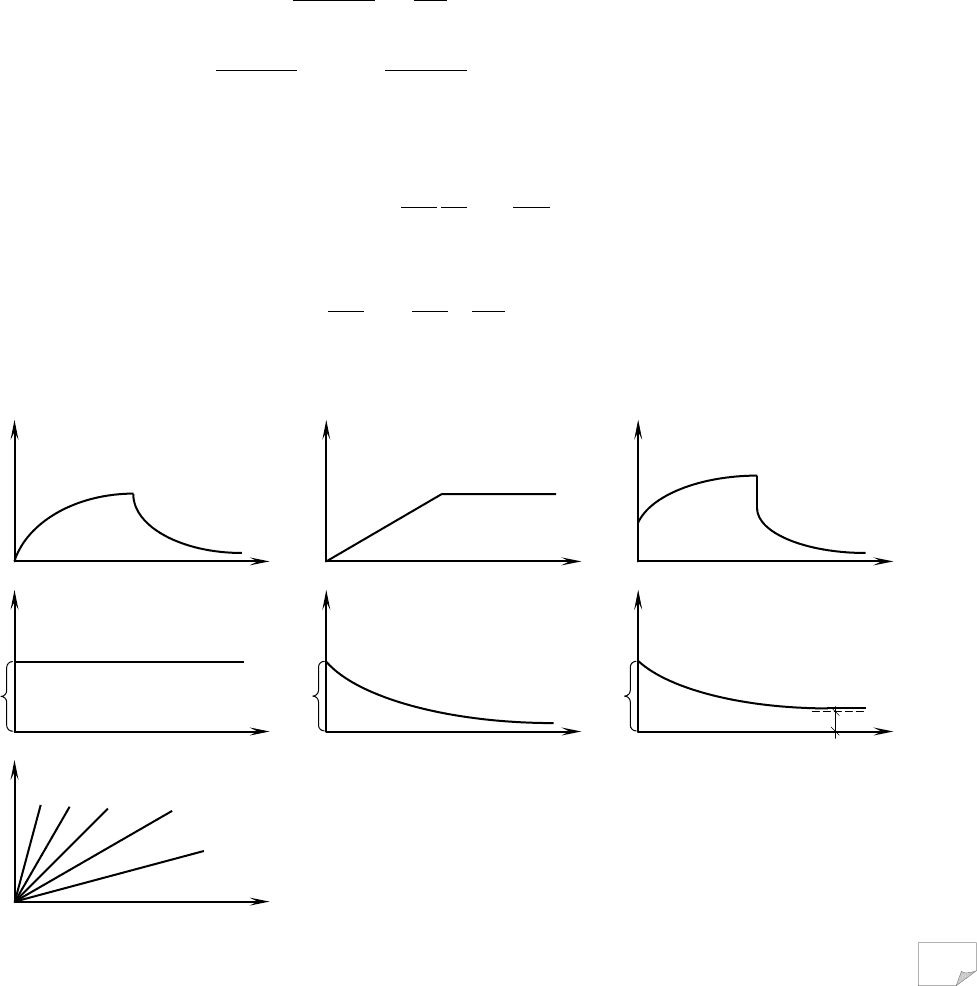
Згідно з (6.16), напруги розслаблюються з часом від початкового значення τ

до нуля

(рис. 6.9, б). При постійній напрузі τ=const вираз (6.15) переходить у рівняння Ньютона

ητγ /



, що відповідає безперервному зростанню деформації з постійною швидкістю (рис.

6.9, б). Тому тіло Максвелла має властивість релаксації, але не проявляє властивості післядії.

Узагальнене пружно-в’язке тіло – це сполучення тіл Кельвіна-Фойгта та Максвелла

(рис. 6.8, в): HP=H

–(H

/N)=H–K, – яке одночасно описує різні боки пружно-в’язкого проце-

су деформування: післядію і релаксацію. Рівняння цієї системи мають такий вигляд:

NHH

ττττ

+==

;

γγγ

;

γγ

. (6.17)

Підставивши в ці вирази значення напруг у відповідних елементах

000

γτ

111

γτ

γητ



, після відповідних перетворень отримуємо

γηγτ



+=+

. (6.18)

Прийнявши

∞

та

, маємо рівняння деформування

γγττ



TGGT

+=+

∞

. (6.19)

При постійному навантаженні τ=const рішення цього рівняння дає

τγ

∞













−=

exp

. (6.20)

Звідси при початковій умові γ=γ

при t=0 отримуємо рівняння пружної післядії

T/t

GGG

−

∞∞













−−=

, (6.21)

де

T)G/G(T

∞

Для t=0 за цим рівнянням маємо γ

=τ/G

, а для t=∞ – γ

∞

=τ/G

∞

. Відповідно (рис. 6.9, в)

γ=const

τ=0

τ=const

τ=0

τ=const

γ=const

∞

τ=0

τ=const

t=0

t=∞

Рис. 6.9. Типовий вигляд графіків повзучості та ре-

лаксації пружно-в’язких тіл: а – Кельвіна-

Фойгта;

б – Максвелла; в – узагальненого пружно-в’язкого;

г – зміни в часі модуля деформації

161

вираз (6.21) можна переписати у вигляді

T/t

e)(

−

∞∞

−−=

γγγγ

. (6.22)

Звідси стає зрозумілим зміст початко-

вого (умовно-миттєвого) G

та кінцевого (гра-

нично-тривалого) G

∞

модуля зсуву (деформа-

ції): перший визначає зв’язок між напругою і

миттєвою деформацією γ

, а другий – між на-

пругою та кінцевою, стабілізованою дефор-

мацією γ

∞

(рис. 6.9, г).

Для випадку розвантаження t=0 вираз

(6.19) дає таке рівняння:













−













−=

exp

γγ

, (6.23)

де t

– час розвантаження; τ

і γ

– напруга й деформація, що відповідають цьому моменту.

При постійній деформації γ=const вираз (6.19) описує релаксацію напруг (рис. 6.7, в):

T/tT/t

e)(e)GG(G

−

∞∞

−

∞∞

−+=−+=

τττγγτ

, (6.24)

де τ

– початкове значення напруги (при t=0); τ

∞

– кінцеве значення напруги (при t=∞).

Таким чином, узагальнене рівняння (6.19) описує як процес пружної післядії, так і

процес релаксації, при цьому на відміну від (6.12) вираз (6.19) ураховує миттєву деформацію,

а на відміну від (6.15) передбачає падіння напруги не до нуля, а до певної кінцевої величини.

Пружно-пластичне тіло Прандтля моделюють послідовним з’єднанням елемента

Сен-Венана і пружного елемента Гука (рис. 6.10, а). Воно показує, що при напругах τ<τ

роз-

вивається пружна деформація γ=τ/G, а при τ=τ

– необмежена деформація γ→∞.

Модель пластично-в’язкого тіла Бінгама складається з пружного H, в’язкого N еле-

ментів й елемента Сен-Венана SV (рис. 6.10, б): B=H–(N/SV). Закономірність його деформу-

вання виводять з умови τ=τ

+τ

при

ττ

γτ G

, (6.25, а) при

ττ

γηττ



=−

. (6.25, б)

Модель іншого пластично-в’язкого тіла Шведова – з’єднання двох пружних елемен-

тів H

і H

з в’язким N та сен-венановим SV елементами (рис. 6.10, в): SW=H

–[(N

-N)/SV].

Рівняння його деформування має такий вигляд:

ττ



−

. (6.26)

Значне розходження між дійсними властивостями реальних ґрунтів та їх модельним

відображенням привело до побудови більш складних багатоелементних моделей із великою

(але кінцевою) кількістю пружних і в’язких елементів. У загальному випадку диференційне

рівняння таких реологічних моделей має вигляд

...

βγβ

ατα

3211

321 ++

++++=++++

, (6.27)

де α

, β

– коефіцієнти, що враховують особливості завантаження й властивості елементів мо-

делі. При

1313

======

...... ββαα

це рівняння переходить у (6.19).

Інший загальний поділ усіх моделей ґрунту пов’язаний із підходом до побудови зале-

жності “напруга – деформація”. З урахуванням того, що ґрунт за своєю природою є не су-

цільним, а дискретним середовищем, його реальною моделлю може бути модель, яка б ста-

тистично описувала взаємодію окремих часток з урахуванням фізичного виду зв’язків між

ними. Цей напрям називають мікропідходом.

Найбільш відомим результатом його є імітаційна ймовірнісна модель І. І. Кандаурова

(більш детально про неї та аналогічні моделі – в книзі: Кандауров И. И. Механика зернистых

сред и ее применение в строительстве. – Л.: Стройиздат, Ленингр. отд-ние, 1988), яка розгля-

дає закономірності розподілу напруг у дискретному сипучому середовищі, виходячи із ста-

Рис. 6.10. Моделі пружно-пластичних

і пружно-в’язких тіл: а –

Прандтля;

б – Бінгама; в - Шведова

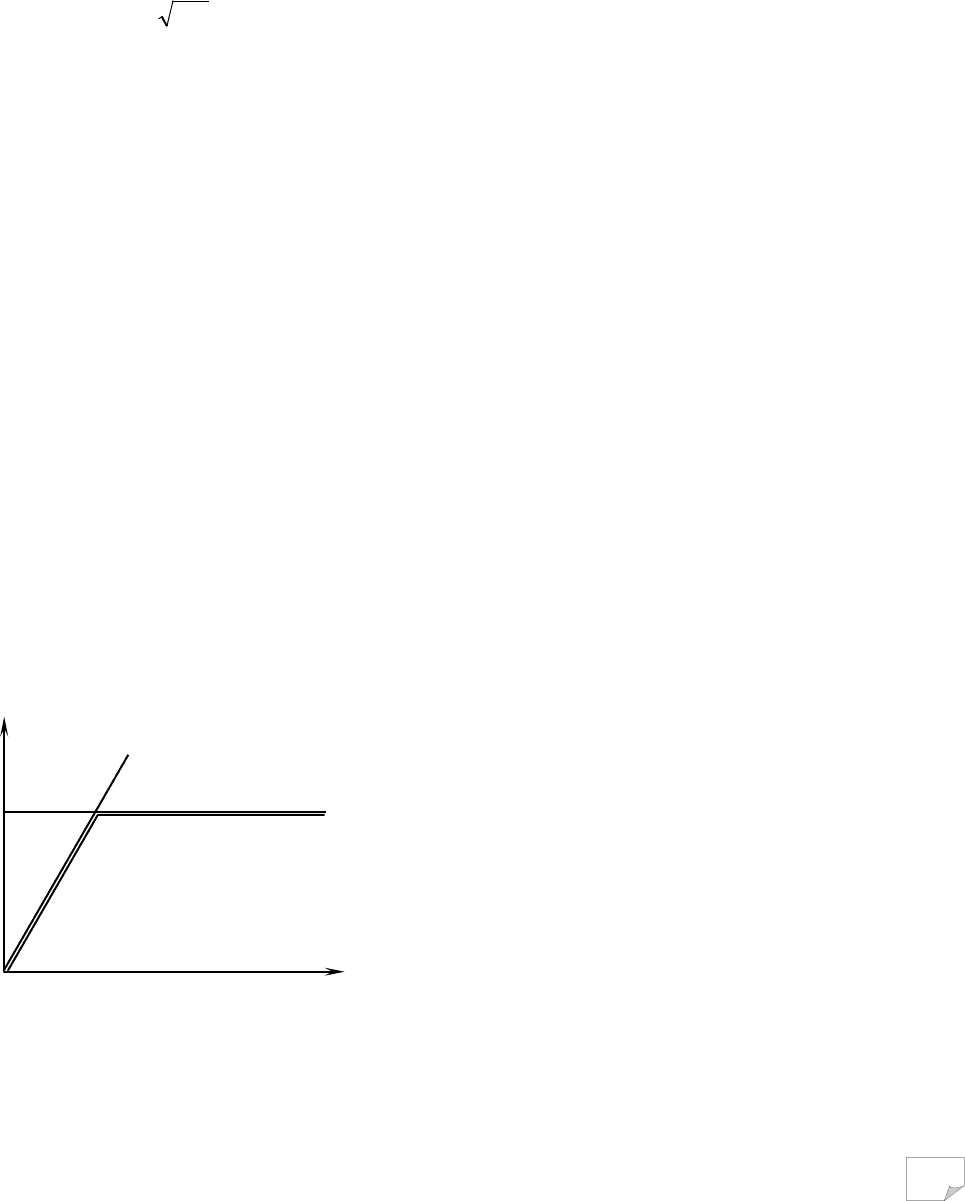
162

тистичного аналізу силової взаємодії часток, що контактують та взаємно проковзуються. Пе-

вною популярністю користується й модель Р. Роу (1962), що описує деформування середо-

вища, яке складається з шарів, на контакті між котрими діють сили тертя. Є й інші цікаві мо-

делі ґрунту (особливо пісків та інших сипучих матеріалів) як дискретного середовища

(Г. І. Покровського, 1937; Р. А. Муллера, 1962; М. Харра, 1977; Б. Й. Дідуха, 1987), але ство-

рення загальної і практичної теорії деформування ґрунтів ще попереду.

Альтернативою мікропідходу є макропідхід, оснований на гіпотезі про безперервність

(континуумі) ґрунтового середовища. При цьому розглядають напруги та деформації нескін-

ченно малих об’ємів і використовують апарат диференціального обчислення, що дає змогу

вивчати НДС усього масиву. Використання для ґрунтових масивів розрахункової моделі су-

цільного середовища передбачає виконання умови, відповідно до якої розміри ℓ елементар-

них об’ємів ΔV (

V∆

=

) ґрунту повинні бути набагато меншими за характерні розміри L

масиву (розміром L можуть бути товщина стислого шару, ширина стрічки завантаження, ви-

сота насипу тощо), отже, ℓ<<L. Ця умова для реальних основ і ґрунтових споруд безперечно

виконується.

Поділ континуальних моделей, звичних для механіки суцільного середовища, можна

провести за багатьма ознаками, зокрема: моделі лінійно деформованого середовища; моделі

теорії граничної рівноваги; моделі пружно-пластичного середовища та теорії пластичної

течії; моделі, що базуються на концепції критичного стану ґрунту, тощо.

Континуальні моделі ґрунтів досить детально розглянуті в підручнику: Механика

грунтов, основания и фундаменты/ С. Б. Ухов и др. – М.: Изд-во АСВ, 1994; книгах: Зарец-

кий Ю. К. Лекции по современной механике грунтов. – Изд-во Ростовского ун-та, 1989; Ры-

жов А. М. Введение в нелинейную механику грунтов и физическое моделирование основа-

ний. – Запорожье: РИП “Видавець”, 1995 і Федоровский В. Г. Современные методы описа-

ния механических свойств грунтов. Обзор. – М.: ВНИИИС, 1985. – Сер. 8, вып. 9.

Моделі лінійно деформованого середовища – найбільш поширені в інженерній прак-

тиці класичної механіки ґрунтів. Умови й обмеження їх застосування перелічені в останньо-

му абзаці п. 6.3. На думку вчених, вони ще будуть конкурувати з більш складними моделями,

особливо в розрахунках масового будівництва. Їх практичне використання розглянуто в роз-

ділі 7. У цих моделях, крім разового завантаження ґрунту і лінійної залежності між напруга-

ми та деформаціями, при навантаженні розглядають лише загальну деформацію без поділу

на пружну й пластичну складові. Перше припущення забезпечує можливість використання

для розрахунків напруг у масиві ґрунту апарату теорії пружності, а друге – при відомих на-

пругах визначення кінцевих деформацій основи.

Отже, моделям лінійно деформованого середовища відповідає не вся крива 0c дефор-

мації ґрунту (рис. 6.1, б), а тільки її ділянка 0a. Тобто застосування теорії лінійного дефор-

мування ґрунту вимагає встановлення межі її ви-

користання. Цією межею в розрахунках напруг і

осідань основ служить переважно середній тиск

під підошвою фундаменту, до досягнення якого

залежність S=f(σ) близька до лінійної. Недотри-

мання цього обмеження звичайно призводить до

заниження величини осідання основ порівно з їх

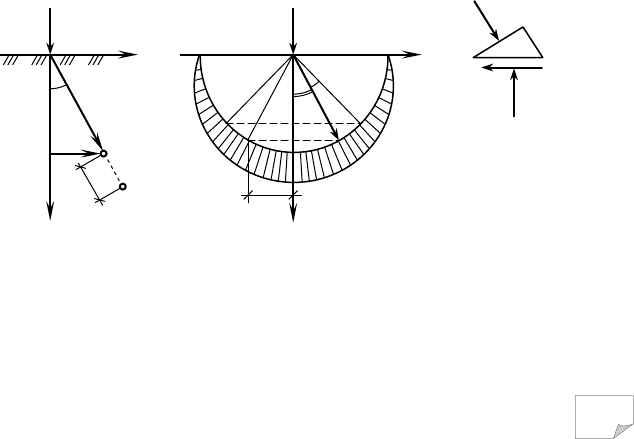
фактичними значеннями. Типовий для моделі лі-

нійно деформованого середовища вигляд графіка

залежності між напругами та деформаціями подано

на рис. 6.11 (лінія 1). Границею лінійного дефор-

мування цієї моделі ґрунту є межа пропорційності

(точка А).

Рівняння стану моделі теорії лінійного де-

формування записують у вигляді узагальненого за-

кону Гука:

Рис. 6.11. Типовий вигляд графіків за-

лежності між напругами (σ) та дефор-

маціями (ε) моделей грунтів: 1 –

лінійно

деформованого середовища; 2 – жорст-

ко-пластичного тіла; 3 – пружно-

пластичного тіла (діаграма Прандтля)

163

[ ]

)(

;)(

;

)(

;)(

;

)(

;)(

zxzxyxzz

yzyzxzyy

xyxyzyxx

γσσνσε

=+−=

121

(6.28)

де E – модуль загальної лінійної деформації; ν – коефіцієнт поперечного лінійного розши-

рення (коефіцієнт Пуассона). Методики отримання цих деформаційних характеристик ґрунту

розглянуті в п. 4.5.

У випадку розвантаження рівняння стану мають той же вигляд, але вміщують інші ве-

личини

′

та

′

, що характеризують лише пружні (які відновлюються) деформації ґрунту.

Нерідко методику лінійно деформованого середовища використовують для розрахун-

ків напруг і деформацій, виходячи з того, що у різних шарах ґрунту, при різних граничних

умовах, механічні властивості неоднакові. Наприклад, модуль деформації приймають змін-

ним за глибиною (Дураев А. Е. Расчет конструкций на грунтовом основании с возрастающим

по глубине модулем деформации. – Саранск: Изд-во Мордов. ун-та, 1991) або враховують

змінність модуля деформації ґрунту в усьому діапазоні тиску, який сприймає основа при на-

вантаженні (Винников Ю. Л., Яковлєв А. В. Пропозиції щодо уточнення розрахунку осідань

основ методом пошарового підсумовування// Будівельні конструкції. – Міжвідомчий науко-

во-технічний збірник. – Вип. 51. – К.:НДІБК, 1999. – С.445-453). Тоді результати розрахунків

стають більш точними, але й більшою складністю стає визначення вихідних механічних ха-

рактеристик у кожному шарі навіть однорідного ґрунту.

Часові процеси в межах моделей лінійно деформованого середовища розглядають у

теорії консолідації (більш детально див. пп. 10.6 і 10.7).

Критерієм застосовуваності моделі лінійно деформованого середовища до ґрунтових

масивів за пропозицією В. А. Флоріна, прийнято ступінь розвитку областей граничного на-

пруженого стану (граничної рівноваги). Якщо такі області відсутні чи малі порівняно з роз-

мірами фундаменту використання цієї моделі вважають допустимим, у протилежному випа-

дку – ні. Зокрема, тепер у розрахунках основ будівель і споруд допускається використання

моделі лінійно деформованого середовища, якщо глибина розвитку областей граничного на-

пруженого стану не перевищує приблизно ¼ ширини підошви фундаменту (для міцних ґру н-

тів та жорстких споруд ця глибина може бути збільшена).

Моделі теорії граничної рівноваги ґрунту відповідають умовам, коли в усіх точках

ґрунтового середовища виконується умова граничної рівноваги, а в елементах масиву пере-

важають пластичні деформації (орієнтовно точка c графіка S=f(p) на рис. 6.1, б). Тоді система

рівнянь стану (при використанні моделі міцності ґрунту Кулона–Мора) для плоскої задачі

набуває вигляду

ϕϕσστσσ

τσ

2222

sin)ctgc()(

zxxzzx

xzx

⋅++=+−

∂

, (6.29)

де c – питоме зчеплення ґрунту; φ – кут внутрішнього тертя ґрунту (див. п. 4.6); X, Y – ком-

поненти об’ємних сил.

Лінія 2 на рис. 6.11 відображає модель жорстко-пластичного тіла. Припускають, що

лінійна (пружна) частина його переміщень (деформацій) дуже мала порівняно з пластичною

складовою. Фізичні рівняння описують граничний напружений стан (граничну рівновагу).

Задачу розрахунку такого тіла вирішують як статично визначену. Переміщення не знаходять,

бо ця модель не містить співвідношень, котрі б зв’язували напруги та деформації. Розраху-

нок спрямовано на визначення, як правило, одного параметра – показника несучої здатності:

граничного навантаження (сили, моменту тощо).

164

Через те, що використання таких моделей не дає змоги визначати деформації середо-

вища, які відповідають моменту настання граничної рівноваги, їх іноді називають “безде-

формативними”. Ще один недолік системи рівнянь (6.29) полягає в тому, що вона дає задо-

вільні результати лише за умови постійності значень характеристик міцності та деформатив-

ності ґрунтів усіх елементів масиву в будь-який момент його роботи. Між тим, у загальному

випадку ці показники змінні як в елементах масиву за глибиною і в плані, так і в кожному з

них при зміні тиску на ґрунт.

У зв’язку з цим часто в розрахунках використовують рішення змішаної задачі теорії

лінійно деформованого середовища та теорії граничної рівноваги. Згідно з ним (моделі

Б. Й. Дідуха, О. Л. Крижанівського, Ю. М. Мурзенка, З. Мруза, К. Роско, А. Скофільда й ін-

ших) рівняння рівноваги виконуються за усім масивом, що розглядають, рівняння сумісності

– в пружній області і рівняння граничної рівноваги – в області пластичних деформацій. Зна-

чення механічних властивостей ґрунтів моделі В. М. Ніколаєвського, О. К. Бугрова,

Д. М. Шапіро та інших коригують урахуванням швидкості дилатансії (див. п. 4.9).

Раціональним застосуванням теорії граничної рівноваги є розрахунки стійкості спо-

руд і основ, укосів, схилів, тиску ґрунту на огорожі (див. розділ 8).

Моделі пружно-пластичного середовища та теорії пластичної течії – це набір рів-

нянь, що визначають границі пружної поведінки середовища й зв’язок деформацій і напруг

(або їх приростів) за межею пружної області. Вони базуються на диференціальних співвід-

ношеннях між напругами та деформаціями й можуть ураховувати закономірності зміни ме-

ханічних властивостей ґрунту як у процесі експерименту, так і в натурних умовах. Для цього

в систему рівнянь пружно-пластичних деформацій уводять функції, що враховують змінні за

ходом експерименту значення модулів зрушення, об’ємної деформації, загальної деформації,

коефіцієнтів Пуассона. Всі ці варіанти пружно-пластичних середовищ відносять до дефор-

маційних теорій.

Компоненти деформацій і напруг у цих моделях поділяють на пружні й пластичні

складові (лінійних) та кутових деформацій. Пружні складові деформацій описують вищена-

веденими диференційними рівняннями рівноваги, рівняннями нерозривності, фізичними рів-

няннями теорії пружності. Пластичні складові описують диференційними співвідношеннями

деформацій і напруг.

Лінія 3 на рис. 6.11 відображає властивості досить поширеної моделі ідеального пру-

жно-пластичного тіла (діаграма Прандтля), що є сполученням рівнянь лінійно деформова-

ного та жорстко-пластичного тіл. У цій моделі межі пропорційності, текучості й міцності збі-

гаються (точка А). Залежність OAB (рис. 6.11) відповідає формам фізичної нелінійності, що

проявляються у безперешкодному деформуванні при граничному напруженому стані: теку-

чості, повзучості, однобічних зв’язках.

Як правило даний клас моделей дає змогу отримувати більш точні результати за ра-

хунок більш чіткої фіксації напруг і деформацій у той чи інший момент навантаження ґрун-

ту. До його проблем відносять використання припущення про ізотропність середовища, чого

немає (згадаймо п. 4.10) навіть у природному однорідному ґрунті, та опис середовища, яке

або лише зміцнюється, або тільки знеміцнюється.

Моделі, що базуються на концепції критичного стану ґрунту (або КС-моделі) (перед

ознайомленням із цим пунктом бажано переглянути п. 4.9), – відносно нова група ґрунтових

моделей, основаних на закономірностях поведінки ґрунту при зсуванні, зокрема зміні його

щільності від початкової до критичної. На сьогодні найбільш відомі дві схеми розроблення

цих моделей:

– перша (моделі В. М. Ніколаєвського, «Cam-clay» (кембріджська глина) Скофільда-Рота та

К. Роско тощо), коли в розрахунок пружно-пластичних деформацій уводять залежність

між швидкістю зміни об’єму та механічними характеристиками ґрунтів. У систему

розв’язуючих рівнянь включають: диференціальне рівняння рівноваги; рівняння гранич-

ної рівноваги; залежність, яка коригує механічні властивості ґрунтів при пластичних де-

формаціях;

165

– друга (модель А. М. Рижова), коли механічні властивості ґрунту визначають безпосеред-

ньо за фіксованими у даний момент часу значеннями щільності природного складу і кри-

тичної щільності. У систему розв’язуючих рівнянь уходять: рівняння зв’язку між почат-

ковими та кінцевими значеннями деформацій; рівняння зв’язку між початковими й кінце-

вими відносними напругами; рівняння зв’язку між безрозмірними параметрами деформа-

цій і напруг; умови граничної рівноваги.

Перевагою КС-моделей є можливість опису з єдиних позицій як зміцнення, так і зне-

міцнення ґрунтів при деформуванні.

У висновку додамо, що ми не розглядали досить специфічні динамічні моделі ґрунтів,

моделі консолідації ґрунту, а також моделі анізотропного середовища. Питання застосування

теорій нелінійного деформування для розв’язання певного класу задач механіки ґрунтів про-

понуються у розділі 9.

7. ЗАСТОСУВАННЯ ТЕОРІЇ ЛІНІЙНОГО ДЕФОРМУВАННЯ

ДЛЯ РОЗВ’ЯЗАННЯ ЗАДАЧ МЕХАНІКИ ҐРУНТІВ

7.1. ВИЗНАЧЕННЯ НАПРУГ У МАСИВІ ҐРУНТУ

ПРИ ДІЇ ЗОВНІШНІХ НАВАНТАЖЕНЬ

Дія вертикальної зосередженої сили (основна задача).

У 1885 p. французьким ученим Ж. Бусінеском була розв’язана задача про

розподілення напруг у ґрунті при дії зосередженої сили. Задача має теоретич-

ний і прикладний характер. Ґрунт у цій задачі уявляється однорідним, ізотроп-

ним, лінійно деформованим напівпростором, що має нескінченне поширення за

глибиною і за площею.

Розглянемо дію вертикальної зосередженої сили N, прикладеної у точці О

до горизонтальної площини, що є поверхнею лінійно деформованого напівпро-

стору (рис. 7.1, а). Під дією цієї сили в усіх точках напівпростору виникає скла-

дний напружений стан. У загальному випадку в кожній точці буде діяти шість

складових напруг. Найбільше практичне значення мають напруги, що діють на

площадках, паралельних поверхні напівпростору: σ

, τ

і τ

Візьмемо довільну точку М

на глибині z і визначимо її положення у по-

лярних координатах. Зрозуміло, що переміщення елементарного об’єму ґрунту

в цій точці під дією сили N буде тим меншим, чим далі вона розташована від

точки прикладання сили, тоб-

то обернено пропорційним ра-

діусу R. У той же час при од-

ному й тому ж значенні R, пе-

реміщення точок будуть неод-

наковими при різних значен-

нях кута β. Переміщення точ-

ки М

будуть максимальними,

якщо кут β дорівнює нулю (на

осі Z). При збільшенні кута β

переміщення зменшуються і

на поверхні ґрунту дорівню-

Рис. 7.1. Схеми дії сил:

а – схема дії зосередженої сили; б – розподіл

напруги

на півкульовій поверхні; в–дія напруги в точці М

dβ

166

ють нулю (β=90°).

Приймемо як постулат, що переміщення точки М

у напрямі радіуса, ви-

ключаючи зону біля точки прикладення сили N, дорівнює

cos

⋅=

, (7.1)

де B – коефіцієнт пропорційності.

Ця залежність може бути виведена із закону всесвітнього тяжіння й задо-

вольняє граничні умови, наведені вище.

Розглянемо тепер точку М

, яка знаходиться на відстані dR від точки М

Переміщення для точки М

dRR

cos

⋅=

. (7.2)

Тоді відносна деформація ґрунту на відрізкові М

-М

RdRR

cosB

dRRRdR

cosB













−=

−

ββ

Нехтуючи величиною RdR, незрівнянно меншою, ніж R

, одержимо

cos

. (7.3)

Згідно із законом Гука, радіальна напруга

⋅=

εσ

, (7.4)

де C – коефіцієнт пропорційності між напругами і деформаціями.

Після підстановки виразу (7.3) у (7.4) одержимо

cos

. (7.5)

Для визначення добутку коефіцієнтів B та C умовно відсічемо частину

напівпростору півкульовою поверхнею (рис. 7.1, б). Складемо рівняння проек-

цій на вісь Z усіх сил, що діють на відсічений елемент, для невагомого середо-

вища. Тоді

∫

=−

βσ dAcosN

, (7.6)

де dA – поверхня елементарного кульового пояса, яка дорівнює

( )( )

ββπ RdsinRdA

Підставляючи вираз для dA в (7.6), одержимо після інтегрування і підста-

новки меж інтегрування

=−

πBCN

Звідси добуток невідомих коефіцієнтів

. (7.7)

Підставляючи вираз (7.7) у (7.5), одержимо

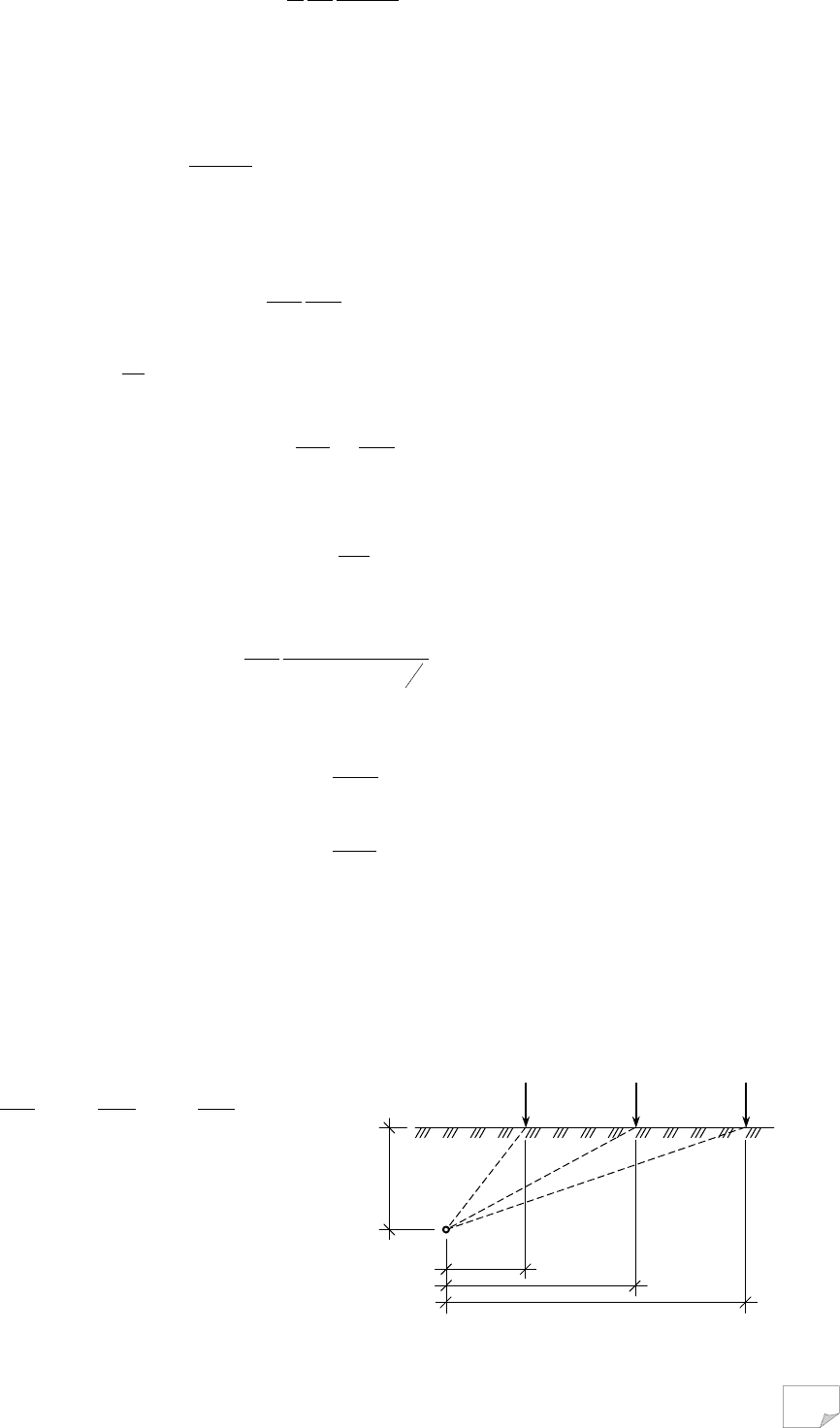
167

cosN

. (7.8)

Напруга σ

діє на похилу площадку dA.

Розглядаючи рівновагу елементарної трикутної призми (рис. 7.1, в), скла-

демо рівняння проекцій усіх сил на вертикальну вісь:

0=−

dAcos

cos

βσ

Після підстановки сюди значення σ

із виразу (7.8) одержимо формулу

для визначення вертикальної напруги

cos

Оскільки

cos

(див. рис. 7.1, а), то

Ураховуючи, що

222

zrR

, одержимо

, (7.9)

де

( )

[ ]

z/r

. (7.10)

Аналогічно знаходимо дотичні напруги:

⋅

;

⋅

Значення коефіцієнта К можна знайти в таблицях залежно від співвідно-

шення r/z.

Якщо на поверхні масиву прикладені кілька зосереджених сил, то, вихо-

дячи з принципу незалежності дії сил, стискуючу напругу для горизонтальних

площадок, паралельних обмежуючій площині, можна визначити простим під-

сумовуванням (рис. 7.2)

++=

, (7.12)

де коефіцієнти K

залежать від співвідно-

шення r

/z.

Визначивши значення напруг в

окремих точках масиву, можна побудувати

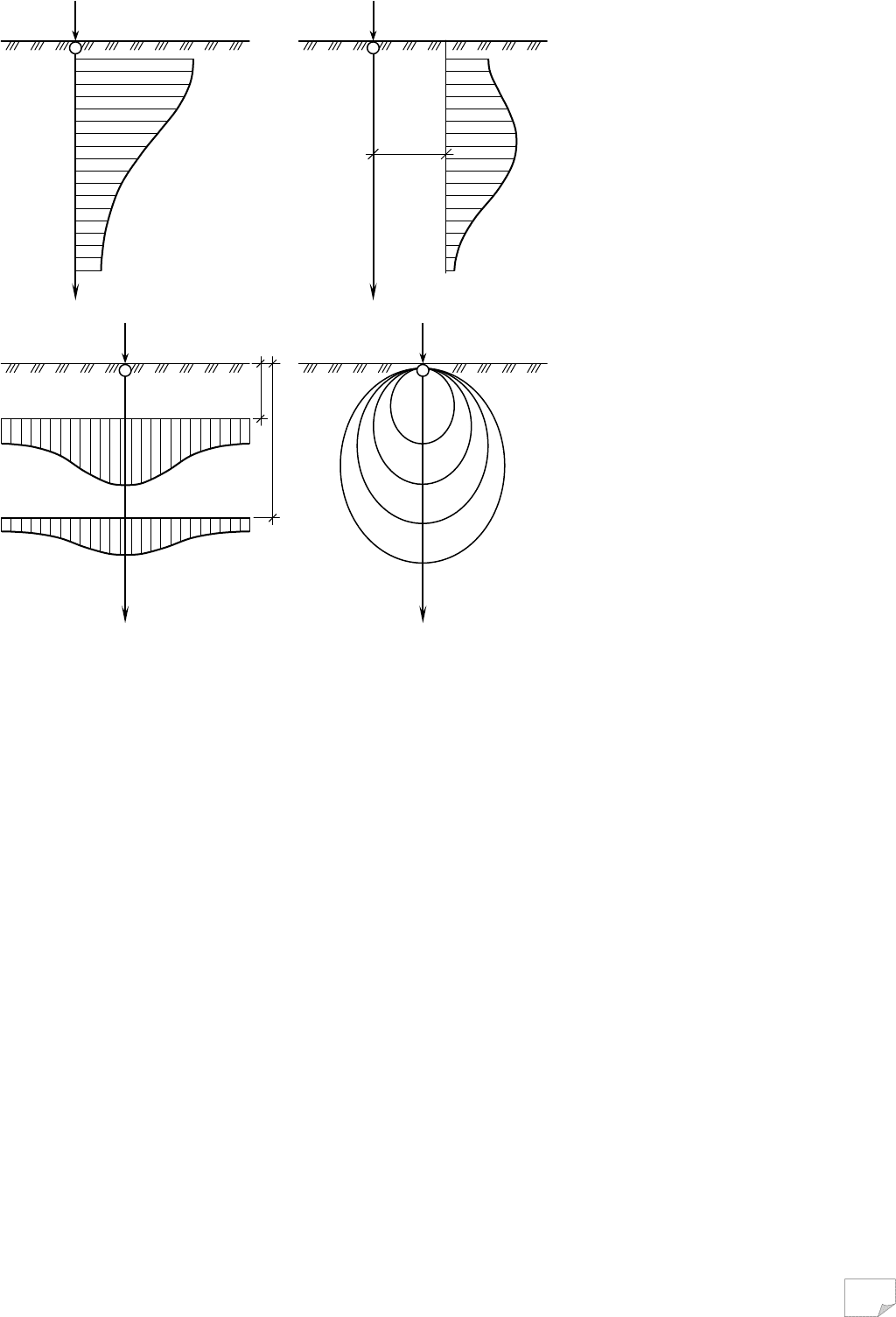
епюри напруг (рис. 7.3).

Якщо розглядати характер зміни

стискуючих напруг σ

по глибині на про-

Рис. 7.2. Схеми дії кількох зосере-

джених сил

168

довженні лінії дії сили N

(рис. 7.3, а), можна поба-

чити, що напруги змен-

шують

ся з глибиною за

нелінійним законом, на-

ближаючись до нуля. При

цьому на ділянці безпосе-

реднього контакту сили N

із ґрунтом спостерігається

незначна за розмірами зо-

на, де теоретичні вирази

для визначення напруги

не можуть бути викорис-

тані через великі значення

напруг, що значно пере-

вищують міцність ґрунту.

Якщо розглядати

характер зміни напруг по

глибині на деякій відстані

r (рис. 7.3, б), то можна

одержати епюру, в якої

через розсіювання напруг

максимальне значення σ

може бути одержане на

деякій глибині від повер-

хні з наступним затухан-

ням.

Визначаючи зміни напруги при віддаленні від лінії дії сили в боки, буду-

ють епюри для необхідних постійних глибин z

, z

і т.д. (рис. 7.3, в). Максима-

льне значення напруга має по осі Z і зменшується за криволінійним законом

при віддаленні від цієї осі. Чим глибше розміщена горизонтальна площина, тим

менші максимальне значення напруг і криволінійність епюри.

Для визначення розміщення в ґрунті зони з однаковим напруженим ста-

ном будують лінії однакових напруг (ізобари), з’єднуючи точки з однаковими

значеннями напруг (рис. 7.3, г).

Дія місцевого рівномірно розподіленого навантаження

У справжніх умовах роботи споруд навантаження на ґрунт не передають-

ся у вигляді зосереджених сил, а розподіляються по площадках обмежених ро-

змірів.

У випадку прямокутної площадки і рівномірно розподіленого наванта-

ження розв’язання в кінцевій формі є тільки для визначення вертикальних нор-

мальних напруг у точках, які розміщуються на вертикалях, що проходять через

центр площадки та її кути.

Найпростіше рішення одержано А. Лявом у 1935 p.

Рис. 7.3. Види епюр напруг від зосередженої сили:

а – за глибиною по осі z; б – за глибиною на відстані r

;

в – відносно горизонтальних площин; г – лінії рівних на-

пруг (ізобари)

=f(z)

z≠0

r=0

=f(z)

r=const

z≠0

=const

z≠0 r≠0

0,1 σ

0,2 σ

0,4 σ

0,6 σ

r≠0

z=const

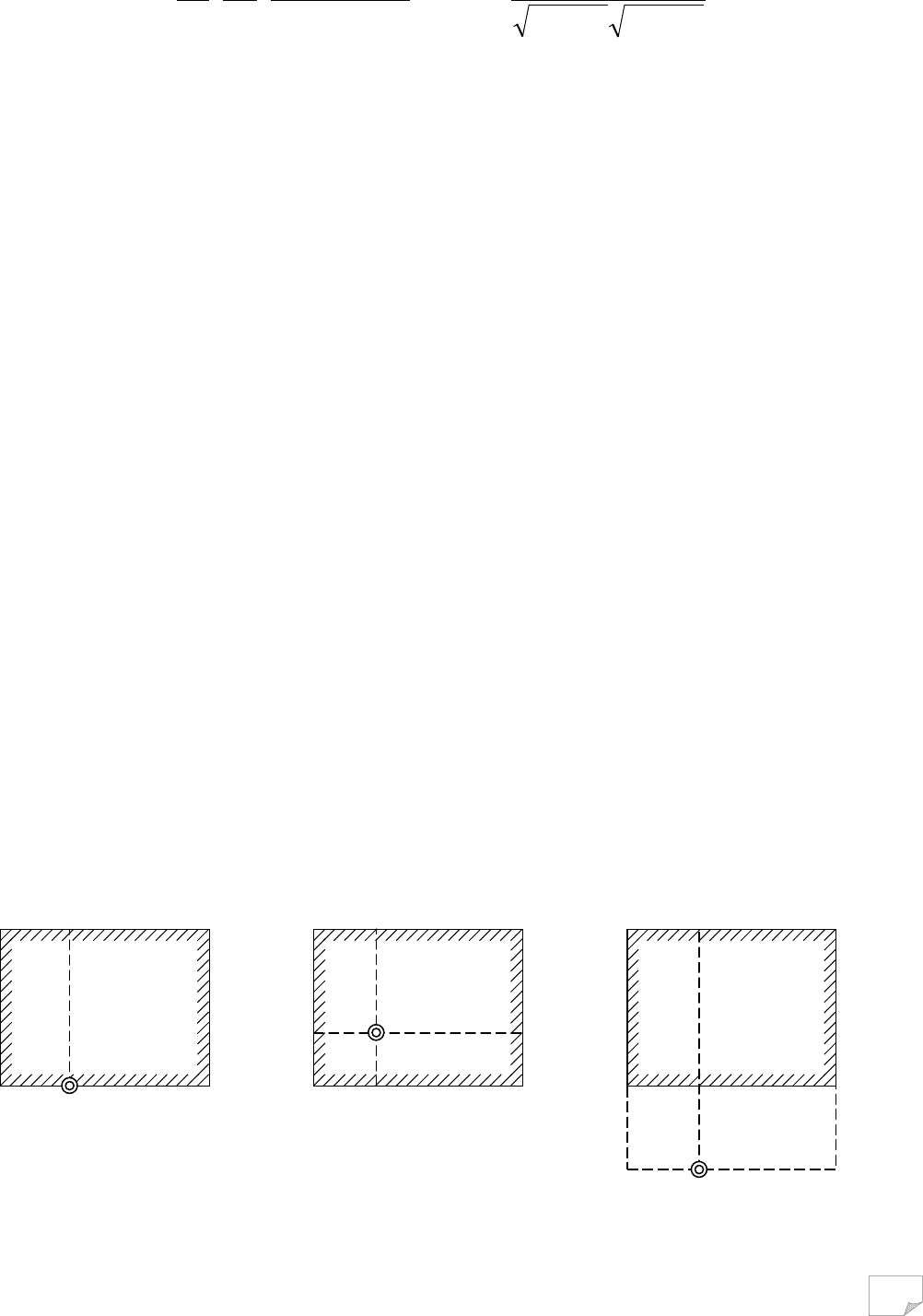
169

Стискуюча напруга для кутових точок

























⋅=

2222

222

zbzr

arcsin

blzD

zbl

lbzp

zс

, (7.13)

де p – інтенсивність рівномірно розподіленого навантаження; ℓ, b – відповідно

довжина і ширина площадки;

22222

zbr)/D(

++== 

Аналогічно визначають напругу σ

під центром завантаженого прямо-

кутника.

Для полегшення розрахунків ці формули приводять до вигляду

czc

⋅=

, (7.14)

⋅=

, (7.15)

де K

і K

– кутові коефіцієнти, які можна знайти в СНиП 2.02.01-83 залежно від

співвідношень 2z/b і ℓ/b. Вирази (7.13)-(7.15) дають точний розв’язок лише для

прямокутної площадки завантаження, деформації якої відповідають деформаці-

ям поверхні лінійно деформованого напівпростору, тобто для умов гнучкого

прикладання навантаження. Реальні умови роботи основ і фундаментів дещо

відрізняються від умов розглянутої задачі, але отримані розв’язки дозволяють із

незначними похибками визначити стискуючі напруги для будь-якої точки напі-

впростору.

Використовуючи кутові коефіцієнти, можна визначити стискуючу напру-

гу на вертикалі, котра проходить через будь-яку точку прямокутника. Цей ме-

тод має назву методу кутових точок. Суть його в тому, що вантажну площу ро-

збивають на такі прямокутники, для яких точка, через яку проходить вертикаль,

є кутовою. Тоді стискуюча напруга в цій точці буде дорівнювати алгебраїчній

сумі напруг від прямокутних площ завантаження, для котрих ця точка є куто-

вою.

Розглянемо три основних випадки застосування методу кутових точок

для визначення стискуючої напруги (рис. 7.4):

1) точка М лежить на контурі прямокутника зовнішнього тиску; 2) точка М ро-

зміщується в середині прямокутника тиску; 3) точка М розташована зовні пря-

мокутника тиску. У першому випадку σ

у точці М визначають як суму кутових

Рис. 7.4.Схема розподілу прямокутної площадки при визначенні

напруг за методом кутових точок: а – точка на контурі площадки;

б – точка в середині площадки; в – точка зовні площадки