Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств

Подождите немного. Документ загружается.

муле (11-100) величину Я можно определить из очевид-

ного соотношения:

/7 =

(у,-т)

+(^-^

)

^+(/?*м-<i

)

1/2

(11-103)

Следует помнить, что для малого зеркала, располо-

женного в зафо'кальнон области, П>й, а в предфокаль-

ной —

IJ<d.

Определив Я по формулам (11-98)

—

(11-100), строят профиль малого зеркала.

в) Двухзеркальные антенны, удовлетворяющие спе-

циальным требованиям. Рассмотренные выше некоторые

виды двухзеркальных антенн являются только неболь-

шой и притом наиболее простой частью возможных ва-

риантов этих антенн. В самом деле, поверхности одного

из зеркал можно придать произвольную форму и найти

форму поверхности второго зеркала исходя из необходи-

мости получить в раокрыве ангенны плоский или какой-

либо иной фронт волны. Рассмотренные выше двухзер-

кальные сферические антенны являются частным слу-

чаем таких антенн.

С помощью двухзеркальных антенн можно решать и

более сложные задачи. Можно, например, потребовать

чтобы распределение как амплитуды, так и фазы поля

в раскрыве антенны удовлетворяло заданным законам

или чтобы антенна представляла собой апланатическую

систему, что позволит в широких пределах перемещать

ДН

пространстве за счет изменения положения источ-

ника.

Строгий расчет таких систем, даже методами геомет-

рической оптики, достаточно сложен, и поэтому часто

прибегают к графическому построению профилей зеркал,

обеспечивающему вполне удовлетворительную точность.

Пусть источник расположен в точке О, являющейся

началом координатной системы (рис. 11-47). Нетрудно

показать, что выполнение какого-либо требования, ука-

занного выше, равносильно заданию соответствия между

углами выхода лучей из источника г|з и точками рас-

крыв а:

у=у{Ъ) или чр=1р(^)- (11-104)

611

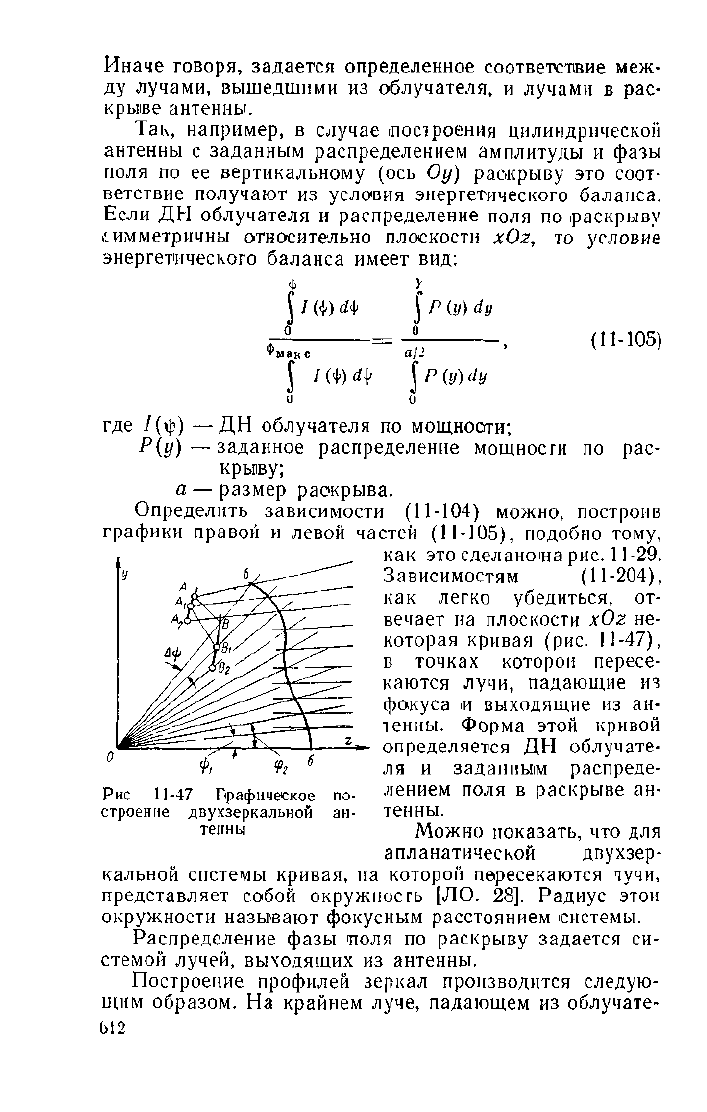
Иначе говоря, задается определенное соответствие меж-

ду лучами, вышедшими из облучателя, и лучами в рас-

крыве антенны.

Так, например, в случае (построения цилиндрической

антенны с заданным распределением амплитуды и фазы

ноля по ее вертикальному (ось Оу) раокрыву это соот-

ветствие получают из условия энергетического баланса.

Если ДН облучателя и распределение поля по раскрыву

симметричны относительно плоскости xOz, то условие

энергетического баланса имеет вид:

(ф)

йф

] Р (у) dy

лаке а/2

J /(ф)<# ^P(y)dy

(11-105)

где 1($)

Р(У)

рас-

•

ДН облучателя по мощности;

заданное распределение мощности по

крьгоу;

а — размер раокрыва.

Определить зависимости (11-104) можно, построив

графики правой и левой частей (11-105), подобно тому,

как это сделано на рис. 11-29.

Зависимостям (11-204),

как легко убедиться, от-

вечает на плоскости xOz не-

которая кривая (рис. 11-47),

в точках которой пересе-

каются лучи, падающие из

фокуса <и выходящие из ан-

тенны. Форма этой кривой

определяется ДН облучате-

ля и заданным распреде-

лением поля в раскрыве ан-

тенны.

Можно показать, что для

апланатической двухзер-

кальной системы кривая, па которой пересекаются тучи,

представляет тобой окружность [ЛО. 28]. Радиус этой

окружности называют фокусным расстоянием системы.

Распределение фазы тюля по раскрыву задается си-

стемой лучей, выходящих из антенны.

Построение профилей зеркал производится следую-

щим образом. На крайнем луче, падающем из облучате-

Ы2

Рис 11-47 Графическое

строение двухзеркальной

по-

ан-

ля,

выбирается некоторая точка А. На выходящем луче,

соответствующем крайнему лучу облучателя, выбирается

точка В (|рис. 11-47). Выбор этих двух точек весьма про-

изволен, но он влияет на форму профилей зеркал, их

размеры и взаимное расположение.

Если соединить точки А и В прямой, то траектория

одного луча системы будет определена, а в точках А и В

можно построить касательные к профилю зеркал. По-

следние перпендикулярны биссектрисам углов между па-

дающим и отраженным лучами в соответствующих точ-

ках.

Касательные к профилю зеркал определяют ориента-

цию плоских отражателей, которые при расположении

их в точках А и В обеспечат нужную траекторию луча.

Если расстояние между лучами не очень велико, то мож-

но считать, что направление касательных к профилю зер-

кал при переходе от первого выбранного луча ко второ-

му изменится незначительно и этим изменением можно

пренебречь. Продолжая касательные в точках Л и В до

пересечения со следующим лучом, получают точки А\

и В[. Соединяя эти точки, получают траекторию следую-

щего луча, и в точках А\ и В\ теперь можно построить

касательные к профилям зеркал, так чтобы обеспечить

полученную траекторию.

Снова продлив касательные до пересечения с после-

дующим, третьим по счету, лучом, получают на нем точ-

ки Ач и В

, в которых строят касательные и т. д.

В результате построения получают ломаную, которая

аппроксимирует профили зеркал. Чем меньше расстоя-

ние между лучами (меньшие углы Аф), тем точнее

аппроксимация. Точность построения можно повысить,

если последующие точки (например, А\ и В\ при выбран-

ных уже точках А я В) выбирать не на пересечении ка-

сательных с лучами, а несколько в стороне (см.

рис.

11-30,6).

Следует отметить, что можно получить рекурентные

выражения для приближенного построения профилей

зеркал по точкам, которые определяют координаты то-

чек А

и В

по известным координатам точек Л

_! и

В работе [Л. 14], например, получены такие рекур-

рентные формулы для синфазной апланатической двух-

зеркальной системы. Однако подобные соотношения ча-

сто достаточно сложны и «вычисления о их помощью уто-

мительны. Поэтому использование графического метода

613

построения профилей зеркал, вполне обеспечивающего

достаточную для практики точность, следует признать

более удобным.

11-11.

ОБЛУЧАТЕЛИ ЗЕРКАЛЬНЫХ АНТЕНН

Облучатель зеркальной антенны является важней-

шим ее элементом, во многом определяющим характери-

стики антенной системы в целом Он представляет собой

небольшую антенну, которая должна удовлетворять сле-

дующим основным требованиям-

Иметь ДН, обеспечивающую надлежащее облуче-

ние зеркала и имеющую минимальный уровень боковых

лепестков.

Иметь минимальные размеры.

Если зеркало фокусирует параллельный пучок лу-

чей в точку (фокус), то иметь фазовый центр

4 Пропускать без пробоя заданную мощность.

5 Иметь требуемую диапазонность.

6 Иметь небольшой вес и достаточную механическую

прочность креплений.

7 Обеспечивать необходимую стойкость к воздейст-

вию метеоусловий и возможность полной герметизации

фидерного тракта

Требования к ДН облучателя во многом определяют-

ся заданными характеристиками антенны. Обычно необ-

ходимо получить заданный коэффициент усиления или

ширину ДН антенны при ее минимальных размерах Для

этого следовало бы выбрать облучатель с такой ДН, ко-

торая обеспечивала бы равномерное распределение

амплитуды поля в раскрыве антенны Однако практиче-

ски такой облучатель изготовить не удается. Более того,

как правило, требуют, чтобы ДН антенны имела малый

уровень боковых лепестков, что возможно получить толь-

ко при спадающем к краям зеркала амплитудном рас-

пределении. При использовании реальных облучателей

амплитуда поля в раскрыве всегвд уменьшается по мере

приближения к краю зеркала. Закон изменения ампли-

туды поля по раскрыву и ее величина на краю могут

быть подобраны путем выбора облучателя и параметров

зеркала С точки зрения повышения коэффициента усиле-

ния антенны и устранения интерференции полей, созда-

ваемых в пространстве зеркалом и непосредственно

облучателем, было бы желательно, чтобы вся энергия

облучателя попадала на зеркало. При этом, однако,

614

края зеркала облучаются весьма слабо, и их роль в соз-

дании ДН антенны незначительна.

Можно показав (§ 11-3), чю для каждого облуча1е-

ля при заданном раскрыве зеркала существует некото-

рый оптимальный угол раскрыва. Этот угол для боль-

шинства используемых на практике облучателей соответ-

ствует ширине ДН облучателя на уровне

—

(9—11) дб

я иже ее максимума. Как правило, требуют, чтобы края

зеркала облучались на уровне 0,1 ДП облучателя по

мощности (—10 дб). При этом уровень первого бокового

лепестка получается не очень большим, а использование

поверхности зеркала достаточно хорошим. При необхо-

димости иметь очень небольшие боковые лепестки уро-

вень облучения краев зеркала нужно уменьшить, но при

этом слетует помнить, что будет ухудшаться использова-

ние поверхности зеркала, что при неизменном размере

раскрыва ведет к уменьшению коэффициента усиления

антенны.

Требование минимального уровня побочных лепест-

ков ДН облучателя связано о тем, что в результате

интерференции поля создаваемого антенной и поля ле-

пестков облучателя ДН антенны может быть искажена.

Если облучатель имеет значительный задний лепесток,

то он может оказать существенное влияние на интенсив-

ность излучения ангенны в направлении ее оси. Чтобы

избежать этого, стремятся к тому, чтобы поле заднего

лепестка было бы в фазе с полем антенны. С этой целью

фокусное расстояние зеркала выбирают кратным нечет-

ному числу четвертей волн

(

/ =

(2т'-\~

-г-,

где т—целое

число), если поле заднего лепестка находится в проти-

вофазе с полем основного лепестка облучателя. В случае,

если поля основного и заднего лепестков облучателя

синфазпы, фокусное расстояние берут равным целому

числу полуволн (/—

2~)'

Требование, чтобы размеры облучателя были мини-

мальными, связано с экранировкой (затенением) раскры-

ва антенны облучателем (§ 11-6).

Облучатель должен излучать волну, имеющую сфери-

ческий фронт. Всякое отклонение поверхности фронта

вблны облучателя от сферической ведет к расфазировке

поля в раскрыве антенны т, следовательно, к уменьше-

615

нию КНД. Следует отметить, что наличие фазового цен-

тра у облучателя существенно облегчает расчет поверх-

ности зеркал других типов, например зеркал с поверхно-

стью двойной «ривизны.

При проектировании зеркальной антенны следует

учитывать, что диапазонносгь антенн этого типа пол-

ностью определяется диапазонностью облучателя и фи-

дерного тракта. На диапазонность также влияет взаим-

ное расположение облучателя и зеркала, так как отра-

женная зеркалом волна вновь попадает в облучатель

и может вызывать рассогласование его с фидерным

трактом.

На механическую прочность облучателя и его креп-

ления следует обратить серьезное внимание. Всякое пе-

ремещение облучателя вызывает соответствующее откло-

нение ДН антенны, что может привести к ухудшению

точности определения положения ДН антенны в про-

странстве. При этом следует помнить, что наличие в рас-

крыве антенны всякого рода устройств для крепления

облучателя вызывает ухудшение параметров антенны, и

поэтому к выбору способа крепления облучателя нужно

подойти особенно внимательно. В антеннах, в которых

предусмотрено механическое перемещение облучателя

с целью управления положением ДН в пространстве,

следует предусмотреть балансировку облучателя, особен-

но при использовании конического сканирования, когда

вынесенный с оси вращения облучатель вращается

с большой скоростью.

Как правило, облучатель закрывают диэлектрическим

кожухом, предохраняющим его от воздействия метео-

условий. В антеннах, устанавливаемых на летательных

апппаратах, такой кожух часто является также устрой-

ством, обеспечивающим герметичность фидерного

тракта.

На практике нашли применение облучатели следую-

щих типов:

Вибраторные.

Волноводно-рупорные.

Щелевые.

Вибраторные облучатели. Вибраторные облучатели

представляют собой систему из активного полуволнового

вибратора и рефлектора в виде диска или пассивного

вибратора, которые применяются для получения одно-

направленного излучения (рис. 11-48, 11-49). Реже

используются многовибраторные облучатели, что объяс-

616

няется их сложностью. Существенным достоинством виб-

раторных облучагелеп являются их небольшие размеры

и, следовательно, незначительное затенение ими раскры-

ва антенны.

В зависимости от типа фидера, подводящего энергию

к облучателю, можно различать две группы вибратор-

ных излучателей:

а) питаемые коаксиальным кабелем;

б) питаемые волноводом.

0,0575 А

•*-0,250\-

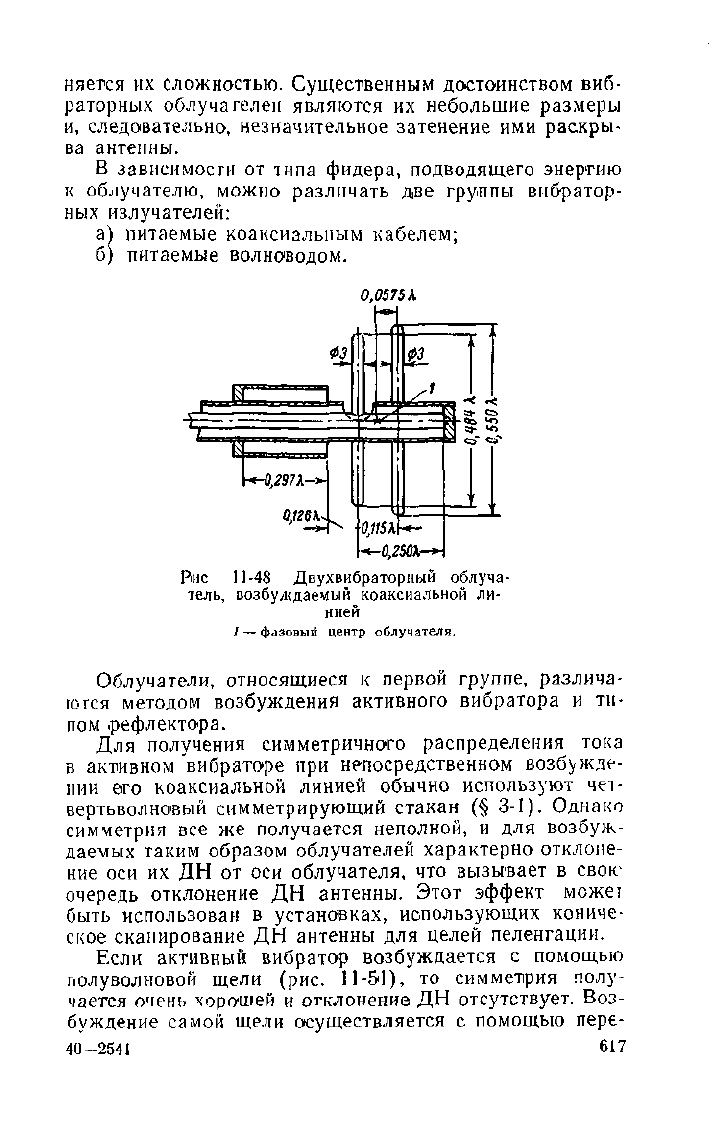
Рис 11-48 Двухвибраторный облуча-

тель,

возбуждаемый коаксиальной ли-

нией

—

фазовьп! центр облучателя.

Облучатели, относящиеся к первой группе, различа-

ются методом возбуждения активного вибратора и ти-

пом (рефлектора.

Для получения симметричного распределения тока

в активном вибраторе при непосредственном возбужде-

нии его коаксиальной линией обычно используют чет-

вертьволновый симметрирующий стакан (§ 3-1). Однако

симметрия все же получается неполной, и для возбуж-

даемых таким образом облучателей характерно отклоне-

ние оси их ДН от оси облучателя, что вызывает в свою

очередь отклонение ДН антенны. Этот эффект может

быть использован в установках, использующих кониче-

ское сканирование ДН антенны для целей пеленгации.

Если активный вибратор возбуждается с помощью

полуволновой щели (рис. 11-51), то симметрия полу-

чается очень хорошей и отклонение ДН отсутствует. Воз-

буждение самой щели осуществляется с помощью пере-

40-2541 617

мычки, соединяющей в пределах щели внутренний и

внешний проводники кабеля Обычно перемычка распо-

лагается на оси вибратора (рис 11-51)

На рис. 11-48 показан цвухвибраторныи облучатель,

возбуждаемый коаксиальной линией с волновым сопро-

тивлением 50 см Такая система имеет фазовый центр,

положение которого указано на рисунке Облучатель

Размера.

9,1

1,593

0,875

0,681

2,875

0,594

0,842

0,177

10,0

1,880

0,984

0,740

3,250

0,657

0,934

0,394

10,7

1,990

1,061

0,7 Т

3,500

0,705

1,000

0,571

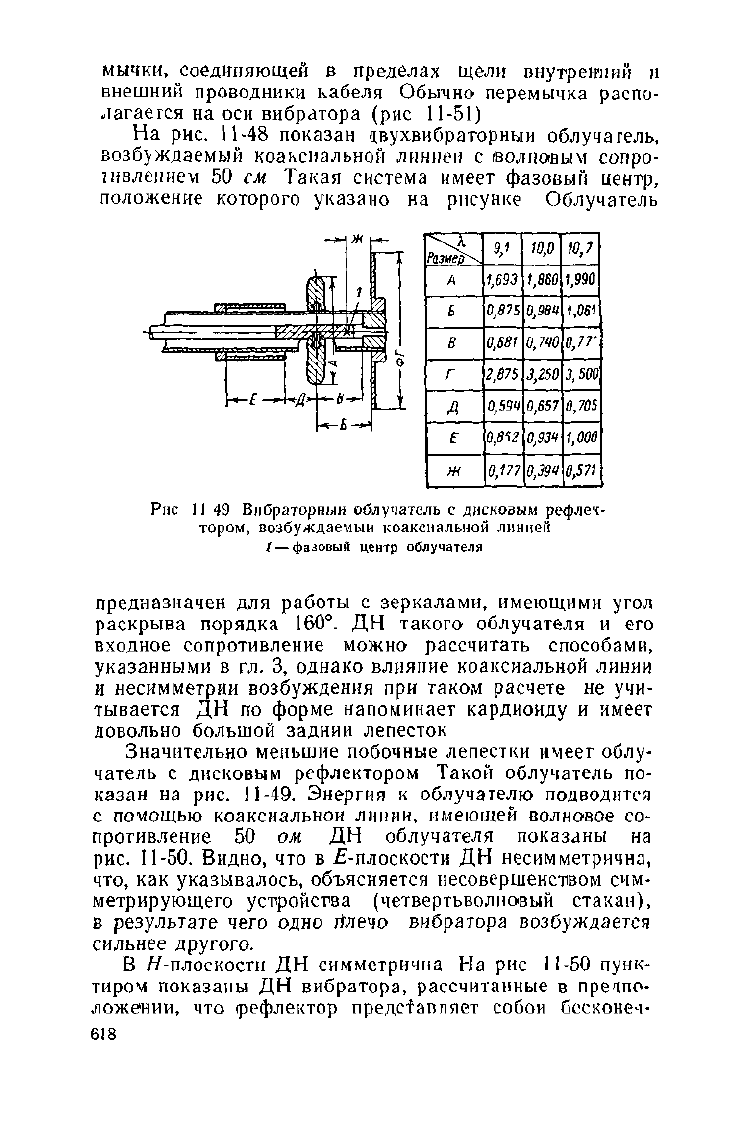
Рис 11 49 Вибраторный облучатель с дисковым рефлек-

тором, возбуждаемый коаксиальной линией

/ — фазовый центр облучателя

предназначен для работы с зеркалами, имеющими угол

раскрыва порядка 160°. ДН такого облучателя и его

входное сопротивление можно рассчитать способами,

указанными в гл. 3, однако влияние коаксиальной линии

и несимметрии возбуждения при таком расчете не учи-

тывается ДН по форме напоминает кардиоиду и имеет

довольно большой задний лепесток

Значительно меньшие побочные лепестки имеет облу-

чатель с дисковым рефлектором Такой облучатель по-

казан на рис. 11-49. Энергия к облучателю подводится

с помощью коаксиальной линии, имеющей волновое со-

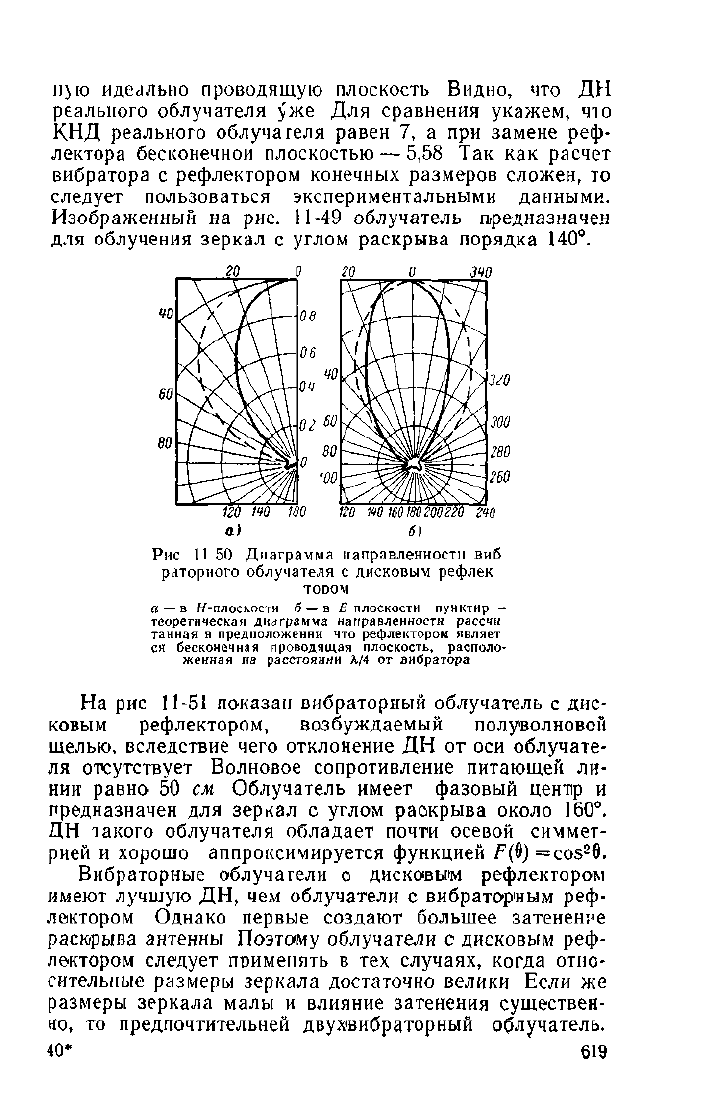
противление 50 ом ДН облучателя показаны на

рис.

11-50. Видно, что в ^-плоскости ДН несимметрична,

что,

как указывалось, объясняется несовершенством сим-

метрирующего устройства (четвертьволновый стакан),

в результате чего одно Ачечо вибратора возбуждается

сильнее другого.

В Я-плоскости ДН симметрична На рис 11-50 пунк-

тиром показаны ДН вибратора, рассчитанные в предпо-

ложении, что рефлектор представляет собой бесконеч-

618

lijio идеально проводящую плоскость Видно, что ДН

реального облучателя уже Для сравнения укажем, что

КНД реального облучателя равен 7, а при замене реф-

лектора бесконечной плоскостью — 5,58 Так как расчет

вибратора с рефлектором конечных размеров сложен, то

следует пользоваться экспериментальными данными.

Изображенный на рис. 11-49 облучатель предназначен

для облучения зеркал с углом раскрыва порядка 140°.

Рис 11 50 Диаграмма направленности виб

раторного облучателя с дисковым рефлек

топом

а — в Я-плоскости б — в Е плоскости пунктир -

теоретическая диаграмма направленности рассчн

тайная в предположении что рефлектором являет

ся бесконечная проводящая плоскость, располо-

женная на расстоянии Л/4 от вибратора

На рис 11-51 показан вибраторный облучатель с дис-

ковым рефлектором, возбуждаемый полуволновой

щелью, вследствие чего отклонение ДН от оси облучате-

ля отсутствует Волновое сопротивление питающей ли-

нии равно 50 см Облучатель имеет фазовый центр и

предназначен для зеркал с углом раскрыва около 160°.

ДН такого облучателя обладает почти осевой симмет-

рией и хорошо аппроксимируется функцией f(6)=cos

Вибраторные облучатели о дисковым рефлектором

имеют лучшую ДН, чем облучатели с вибраторным реф-

лектором Однако первые создают большее затенение

раскрыта антенны Поэтому облучатели с дисковым реф-

лектором следует применять в тех случаях, когда отно-

сительные размеры зеркала достаточно велики Если же

размеры зеркала малы и влияние затенения существен-

но,

то предпочтительней двух'вибраторный облучатель.

40*

619

Мощнос1Ь, пропускаемая вибраторным облучателем,

в основном определяется фидером и может достигать

300—350 кет в импульсе при нормальном давлении.

У вибраторов, возбуждаемых щелью, пропускаемая

мощность несколько ниже, так как она определяется ма-

ксимально допустимым напряжением между краями

щели.

о.жх-

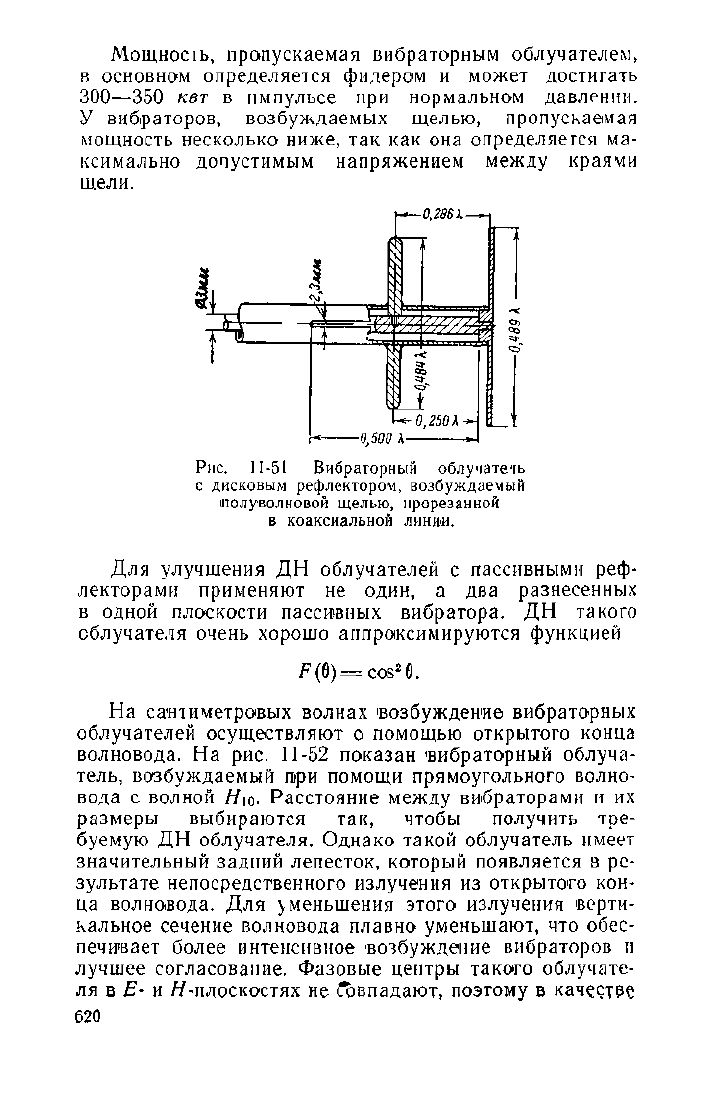
Рис.

11-51 Вибраторный облучатель

с дисковым рефлектором, возбуждаемый

полуволновой щелью, прорезанной

в коаксиальной линии.

Для улучшения ДН облучателей с пассивными реф-

лекторами применяют не один, а два разнесенных

в одной плоскости пассивных вибратора. ДН такого

облучателя очень хорошо аппроксимируются функцией

F (6)

cos

б.

На сантиметровых волнах возбуждение вибраторных

облучателей осуществляют о помощью открытого конца

волновода. На рис. 11-52 показан вибраторный облуча-

тель,

возбуждаемый при помощи прямоугольного волно-

вода с волной Ню. Расстояние между вибраторами и их

размеры выбираются так, чтобы получить тре-

буемую ДН облучателя. Однако такой облучатель имеет

значительный задний лепесток, который появляется в ре-

зультате непосредственного излучения из открытого кон-

ца волновода. Для уменьшения этого излучения верти-

кальное сечение волновода плавно уменьшают, что обес-

печивает более интенсивное возбуждение вибраторов и

лучшее согласование. Фазовые центры такого облучате-

ля в Е- и Я-плоскостях не Совпадают, поэтому в качестве

620