Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств

Подождите немного. Документ загружается.

путем вращения образующей параболы вокруг оси О',

находящейся за зеркалом В этом стучае главный лепе-

сток ДП формируется верхней частью зеркала, а косе-

Кансная часть — нижней Однако такой профиль зерка-

ла менее удобен и на практике не используется

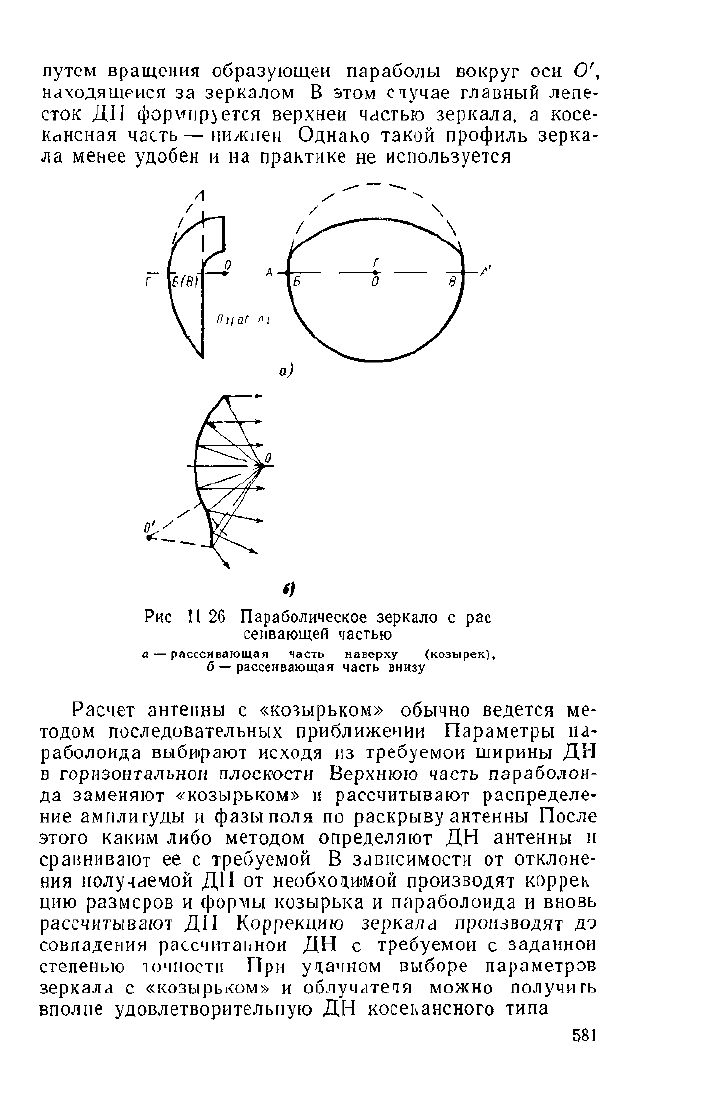
Рис 11 2G Параболическое зеркало с рас

сеивающей частью

а — рассеивающая часть наверху (козырек),

6 — рассеивающая часть внизу

Расчет антенны с «козырьком» обычно ведется ме-

тодом последовательных приближении Параметры па-

раболоида выбврают исходя из требуемой ширины ДН

в горизонтальной плоскости Верхнюю часть параболои-

да заменяют «козырьком» и рассчитывают распределе-

ние амплитуды и фазы поля по раскрыву антенны После

этого каким либо методом определяют ДН антенны и

сравнивают ее с требуемой В зависимости от отклоне-

ния получаемой ДП от необходимой производят коррек

цию размеров и формы козырька и параболоида и вновь

рассчитывают ДП Коррекцию зеркала производят до

совпадения рассчитанной ДН с требуемой с заданной

степенью точности При удачном выборе параметров

зеркала с «козырьком» и облучатетя можно получить

вполне удовлетворительную ДН косекансного типа

581

Антенна в виде параболоида с «козырьком» имеет

ряд недостатков. Как правило, ДН таких антенн имеет

значительные провалы; волна, отраженная «козырь-

ком»,

направлена на облучатель, что требует примене

ния согласующих устройств, которые обычно узкополос-

ны.

Следует также отметить, что отраженная от такого

зеркала волна имеет значительную паразитную поляри-

зацию, а это приводит к снижению КУ антенны. Несмот-

ря на эти недостатки, подобные антенны находят приме-

нение па практике.

Можно создать косекансную ДН, изменяя часть по-

верхности параболоида различными способами. Однако

полным решением задачи будет конструирование специ-

ального зеркала, вся поверхность которого определена

из условия получения ДН заданной формы.

в) Зеркало двойной кривизны и цилиндрическое зер-

кало специальной формы. Рассмотренное выше зеркало

в виде параболоида с «козырьком» имеет поверхность

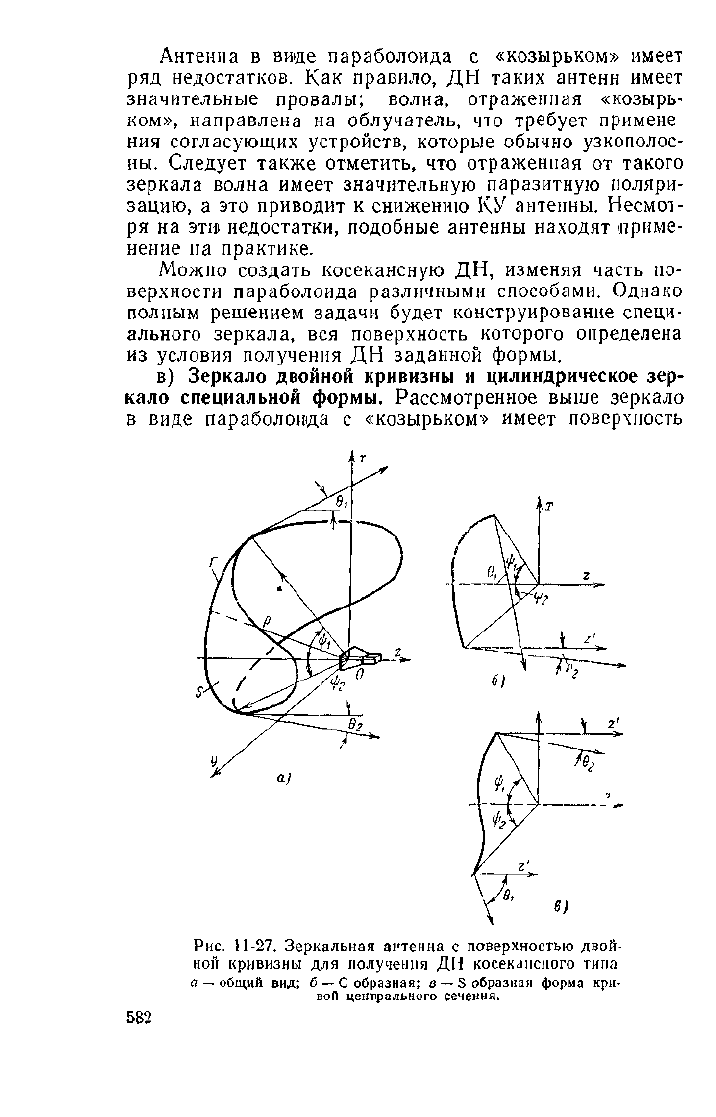
Рис.

11-27. Зеркальная антенна с поверхностью двой-

ной кривизны для получения ДН косекапспого типа

—

общий вид; б

—

С образная; в

—

S образная форма кри-

вой центрального сечения.

582

Рис.

11-28 Антенна с ци-

линдрическим зеркалом для

получения ДН косекансного

типа

У —

цилиндрическое зеркало;

—

линейный облучатель.

11-28).

Антенны с ци-

в изготовлении и на-

двойной кривизны. Однако ниже под зеркалами с поверх-

ностью двойной кривизны будут пониматься такие зер-

кала, вся поверхность которых определена из условия

получения косекансной ДН. В качестве облучателя та-

кого зеркала используется небольшой по размерам

источник электромагнитных

волн

—

рупор, волноводновиб-

раторный облучатель и т. п.

(рис.

11-27).

Частным случаем зеркала

двойной кривизны является

зеркало в виде цилиндра, на-

правляющая которого также

определена из условия получе-

ния ДН нужной формы. В ка-

честве облучателя такого зер-

кала используют линейные из-

лучатели: сегментпо-параболи-

ческую антенну, волповодно-

щелевые и волноводно-вибра-

торпые антенны и т. п. (рис.

линдрическим зеркалом проще

стройке, так как ДН в разных плоскостях формируется

различными элементами (в горизонтальной плоскости—

линейным облучателем, а в вертикальной — зеркалом).

Однако вес и габариты такой антенны относительно ве-

лики и «ри больших длинах волн и узких ДН они могут

оказаться неприемлемыми. Зеркала двойной кривизны

в этом отношении более удобны.

Строгое, электродинамическое, решение задачи об

определении поверхности зеркала представляет значи-

тельные трудности. Однако для синтеза антенн с косе-

кансными ДН удается с успехом использовать методы

геометрической оптики. Хотя решение и является прибли-

женным, но точность его часто оказывается с практиче-

ской точки зрения вполне удовлетворительной. При опре-

делении поверхности зеркала используется следующее

положение геометрической оптики —угловая плотность

энергии при отражении от изогнутой поверхности изме-

няется, причем в случае выпуклой поверхности она

уменьшайся, а при вогнутой увеличивается.

Обычно диаграмма антенны в той плоскости, в ко-

торой она узкая (горизонтальной), симметрична, так же

как и диаграмма направленности облучателя, причем

оси их совпадают. Поэтому поверхность зеркала S долж-

583

на быть симметричной относительно вертикальной пло-

скости, проходящей через оси этих диаграмм. Пересече-

ние этой плоскости с поверхностью зеркала представ-

ляет собой кривую центрального сечения Г (рис. 11-27,о).

Дифференциальное уравнение кривой Г в полярной

системе координат имеет вид:

=tg

^m,

53)

где

— угол между горизонталью и отраженным от зер-

кала лучом (рис. 11-27,а).

Если известна зависимость

(«}>),

то уравнение кри-

вой центрального сечения находят из выражения

|tgjL^(*)

. (11-54)

Зависимость

6 (ф)

можно найти из условия равенства

энергии в трубке лучей (энергетического баланса), которое

в рассматриваемом случае имеет вид:

kI(^)d-b = P(r))

df); (11-55)

здесь /(ф)

—

известная ДН облучателя по мощности.

(d) —

задананя ДН косекансного типа, a k

—

постоянный

коэффициент, который определяется из условия равенства

полной энергии, падающей на зеркало, полной энергии,

отраженной от него:

JP(6)

* = °i (11-56)

'/(Ф) Р/(Ф)

J PW)

Ф.

Однако определить величину этого коэффициента нельзя,

так как неизвестна функция

= р(ф).

584

Для определения искомого соотношения

(ф) можно

воспользоваться приближенным способом расчета по сле-

дующей схеме. Из (11-55) и (11-56) следует:

fp(8)d8

Фа

Г/(Ф)

J г

(Ф)'

Ртл=1

^^---

<п

57)

;<*Ф

где г—относительный радиус-вектор кривой

Г,

равный:

г№=

-Р>.

(И-58)

здесь р

—

наибольшее значение радиуса-вектора кривой Г,

так что всегда

< 1. Интеграл

знаменателе правой

части (11-57) можно представить

другом виде:

]

}

7§)

^=ir]

(П-59)

Ф1

4>i

где

некоторый постоянной коэффициент, причем /i<M.

Теперь соотношение (11-57) можно записать следую-

щим образом:

РШ^-Шьк,

(и-60)

где

P(0)d8

*=£

•

(ц-61)

f/(4>)<*Ф

Ф.

Коэффициент К можно вычислить путем интегрирова-

ния известных функций Р(Щ и /(ф).

Выбрав некоторое значение для г,,

(например, 0,9]

задаваясь приращением угла

—

Д<]/

(порядка

1 —

3°),

можно определить величину Р(б)Дб'

из

соотношения

[см.

(11-60)]:

(

)

Д0'

-^^1^,

(11

62)

585

для одной из крайних точек зеркала, соответствующей,

например, углам 6, и <|v В (11-62) Г (t)

—

среднее значе-

ние функции /(ф) в интервале Дф'- Построив график

функции

и зная величину Р'

(6)

ДО',

т. е. величину интеграла 6

-f

Д8'

j/>(6)tf6,

мы можем найти приращение угла О(Дб'), соответствую-

щее выбранному приращению угла ф(Д'К). Используя за-

тем соотношение (11-53), можно найти приращение радиу-

са-вектора кривой Г

Дг' = г

ДфЧ

Ц^, (11-63)

а по нему и радиус-вектор второй точки зеркала

Таким образом, координаты второй точки зеркала из-

вестны:

Известен также и угол 6, соответствующий этой

точке:

Дб'.

Знание этих трех величин: г', т|/ и 6'—позволяет

применить приведенный выше способ для нахождения

следующей, третьей, точки зеркала и г. д. При правиль-

но выбранном значении коэффициента h в конце расчета

должно получиться, что углу T)i=ip2 соответствует угол

Если это не так, то, значит, величина коэффи-

циента h выбрана неправильно и следует расчет повто-

рить,

взяв новое значение h. Если величина полученного

превышает требуемое, го это означает, что выбран-

ное значение h велико и его нужно уменьшить. Наобо-

586

рот, если полученный угол б

меньше заданного, то вели-

чину коэффициента h следует увеличить.

Из приведенного приближенного способа расчета

ясно,

что его точность тем выше, чем меньше выбранная

величина приращения Дгр угла т|з. Для первых расчетов,

имеющих целью уточнение значения коэффициента h,

можно брать достаточно большую величину Дтр (5—8°).

Однако и в последующем не следует стремиться к очень

большой точности расчета, ибо сам метод построения

зеркала по законам геометрической оптики является

приближенным. Можно показать, что точность расчетов

будет вполне удовлетворительной, если дуга вдоль кри-

вой центрального сечения, соответствующая прираще-

нию А\|), будет «порядка полуволны.

Приведенный выше способ нахождения зависимостей

6(т|))

и r=r(ij)) можно несколько видоизменить.

В уравнении (П-57) можно положить r = const. Тогда

P(9)tf9 __ /(ФИФ И1-64)

(в)

rf8 j /

(ф)

4ф

Эго соотношение имеет место при расчете цилиндри-

ческих зеркальных антенн со специальной формой диа-

граммы направленности, для которых уравнение энерге-

тического баланса имеет более простой вид:

/(ф)й<[» = АР(в)<Й. (11-65)

Так как в (11-65) функции Р(Ь) и /(ф) известны, то зави-

симость

б (ф)

легко найти из соотношения, следующего

из (11-65):

* |/(ФИФ „

|/(Ф)^=Й |/W0. (П-66)

Ф. [Р (6)

rf8

Последнее соотношение выражает условие энергетиче-

ского баланса для всех соответствующих друг другу сек-

торов ДП облучателя (гр—1\ц) и ДН антенны

(б —

б,)

Функции Р(0) и /(Чр) обычно заданы графически, и

для выполнения интегрирования в

(1*1 -66)

удобно приме-

587

пять графическое интегрирование [Л. 8]. Результаты ин-

тегрирования представлены на рис. 11-29 в виде графи-

ков,

построенных в прямоугольной системе координат

с общей осью ординат. Пользуясь этими графиками, на-

ходят зависимость 6—6(ф). Знание этой зависимости

дает возможность проинтегрировать правую часть соот-

град

-50 -40 -30 -20 -10

10 20 30 40

о "] го зо "О ьо so

?о

во но

epcj

Рис.

11-29 Результаты интегрирования ДН

косекансного типа и ДН облучателя.

ношения (11-54) и получить уравнение кривой, которая

является направляющей цилиндрического зеркала (про-

филем зеркала).

Однако целесообразнее построить эту кривую гра-

фическим путем. Для этого выбираем некоторую вели-

чину р

радиуса-вектора определяемой кривой, который

соответствует углу \(ц. Так как для угла

\\>i

известен

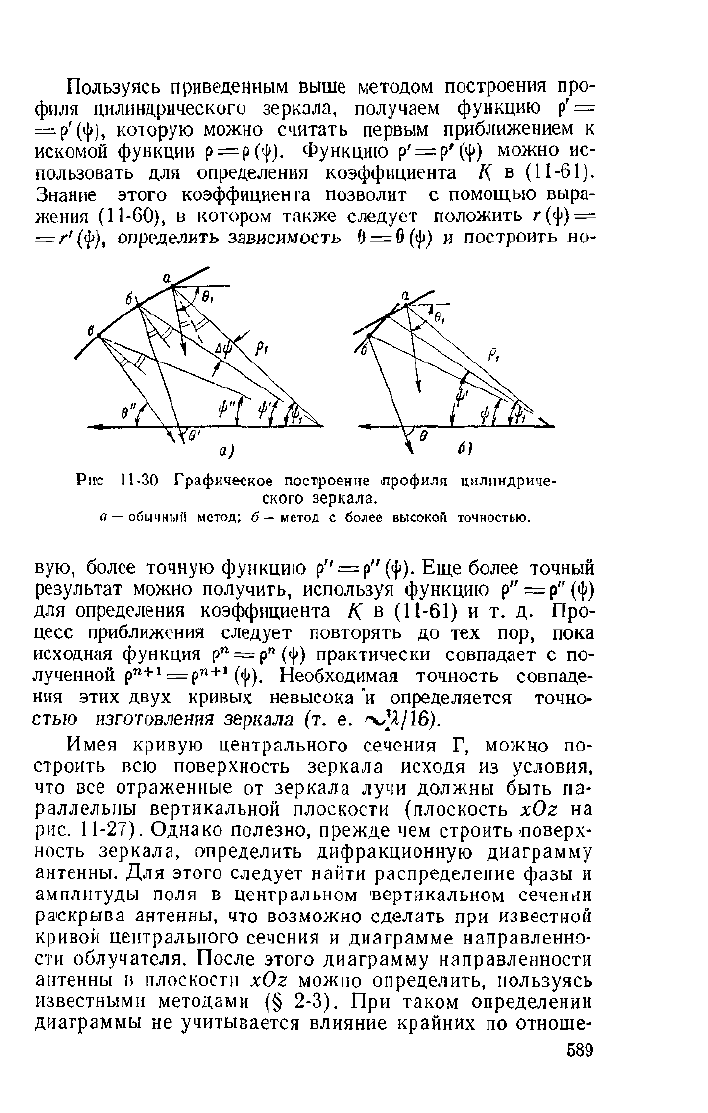
угол 6j, то в точке а (рис. 11-30,а) можно построить

касательную к истинной кривой в этой точке. Выбрав не-

которое приращение Дф угла г(з и считая, что на этом

интервале наклон касательной не изменяется, получаем

точку б. С помощью графиков рис. 11-29 определяем

угол 6', соответствующий углу i|/ =

\pi—Агр.

В точке б

можно также построить касательную к кривой и т. д.

В полученную в итоге таких последовательных построе-

ний ломаную линию вписывается плавная кривая, кото-

рая и является искомой кривой.

Точность такого построения будет тем выше, чем

меньше интервал Arji. Однако и здесь справедливы за-

мечания относительно величины Ai|-, сделанные выше.

С целью повышения точности построения можно точ-

ку б выбирать не в точке пересечения касательной

к искомой 'кривой в точке а с прямой

i[)

= const, а не-

сколько смещая ее в сторону, так чтобы касание к иско-

мой кривой в точках а я б пересекалось при некотором

значении угла ip", причем \|i<i|/<ipi (рис. 11-30,6).

588

Пользуясь приведенным выше методом построения про-

филя цилиндрического зеркала, получаем функцию

р'

—

р'(ф),

которую можно считать первым приближением к

искомой функции

р(ф).

Функцию

р'

= р'(ф) можно ис-

пользовать для определения коэффициента К в (11-61).

Знание этого коэффициента позволит с помощью выра-

жения (11-60), в котором также следует положить г(ф) =

= г'(Ф), определить зависимость

= 6(ф) и построить но-

Pirc 11-30 Графическое построение профиля цилиндриче-

ского зеркала.

а — обычный метод; б

—

метод с более высокой точностью.

вую,

более точную функцию

р"

р"(ф).

Еще более точный

результат можно получить, используя функцию

р"

(ф)

для определения коэффициента К в (11-61) и т. д. Про-

цесс приближения следует повторять до тех пор, пока

исходная функция

(ф) практически совпадает с по-

лученной

n+1

(ф). Необходимая точность совпаде-

ния этих двух кривых невысока "и определяется точно-

стью изготовления зеркала (т. е. '>Л/16).

Имея кривую центрального сечения Г, можно по-

строить всю поверхность зеркала исходя из условия,

что все отраженные от зеркала лучи должны быть па-

раллельны вертикальной плоскости (плоскость xOz на

рис.

11-27). Однако полезно, прежде чем строить поверх-

ность зеркала, определить дифракционную диаграмму

антенны. Для этого следует найти распределение фазы и

амплитуды поля в центральном вертикальном сечении

раскрыва антенны, что возможно сделать при известной

кривой центрального сечения и диаграмме направленно-

сти облучателя. После этого диаграмму направленности

антенны и плоскости xOz можно определить, пользуясь

известными методами (§ 2-3). При таком определении

диаграммы не учитывается влияние крайних по отноше-

589

нйю к плоскости xOz участков зеркала. 'Это, однако, не

приводит к серьезным ошибкам, так как распределение

поля на участках, расположенных вблизи кривой цен-

трального сечения, близко к найденному, а остальные

отражают меньшую часть излучаемой антенной мощно-

сти.

Поэтому можно считать, что диаграмма антенны

в вертикальной плоскости полностью определяется рас-

пределением поля в центральной части антенны. Срав-

нивая полученную диаграмму с заданной, можно сде-

лать вывод о необходимых изменениях вертикального

размера раскрыва антенны и формы кривой центрально-

го сечения. Если, например, диаграмма получилась ши-

ре требуемой, то размер раскрыва следует увеличить,

если же диаграмма уже, чем это необходимо, то раскрыв

уменьшают, и т. п.

После того как окончательно определена кривая цен-

трального сечения, можно построить всю поверхность

зеркала.

Если облучатель имеет фазовый центр, то поверх-

ность зеркала можно найти следующим 'путем. Располо-

жим в фазовом центре облучателя начало координат

(рис.

11-31). Луч, лежащий в плоскости xOz (плоскость

симметрии) и образующий с осью Oz угол т|з, отразится

от точки зеркала Р, принадлежащей кривой центрально-

го сечения Г, под некоторым углом 6- Плоскость, пер-

пендикулярная плоскости xOz « проходящая через отра-

женный от зеркала луч, пересечет поверхность зеркала

по некоторой кривой у. Учитывая параллельность отра-

женных лучей плоскости xOz, можно найти уравнение

этой кривой, которое имеет вид {Л. 9]:

(

Ш>.].

(11-67) г/

4тг)

pcos-

В этом выражении

т)

— координата, отсчитываемая от

зеркала вдоль отраженного луча, лежащего в плоско-

сти Q на рис.

11-31.

Уравнение (11-67) есть уравнение

параболы, имеющей фокусное расстояние, равное:

/ =

cos

(

-i±^-.

(11-68)

Таким образом, каждой точке кривой центрального се-

чения Г соответствует своя парабола, причем эти пара-

болы лежат в плоскостях, перпендикулярных координат-

ной плоскости хОу и образующих с плоскостью yOz

угол б.

590