Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств

Подождите немного. Документ загружается.

Глава

ЩЕЛЕВЫЕ АНТЕННЫ

4-1.

ЩЕЛИ, ПРОРЕЗАННЫЕ В ПЛОСКИХ ЭКРАНАХ

Параметры одиночной щелевой антенны могут быть

определены с помощью принципа двойственности, впер-

вые сформулированного для щелей в плоских экранах

Пистолькорсом [Л. 1, 2]. Строго говоря, он справедлив

для случая щели, прорезанной в безграничной идеально

проводящей плоскости, однако практически им можно

пользовался для большинства щелевых антенн.

Принцип двойственности применительно к щелевым

антеннам гласит: векторы Е и Я поля щелевой антенны,

прорезанной в безграничном плоском экране, имеют та-

кое же направление в пространстве и являются такими

же функциями координат, как векторы Я и —Е поля

симметричного ленточного вибратора, имеющего такие

же размеры, как и щель, и распределение плотности

тока, такое же, как распределение тангенциальной со-

ставляющей напряженности электрического поля по

щели.

Следовательно, ДН узкой прямой щелевой антенны

в безграничном экране такая же, как у симметричного

вибратора. Поляризация поля перпендикулярна по отно-

шению к поляризации поля вибратора.

Полная проводимость щелевой антенны и входное

сопротивление определяются через параметры эквива-

лентного симметричного вибратора:

у 2п "i -f tfi

вх

(60п)

— (60л)

_ (60к)

(

]

)

181

Прямоугольная щель. Для узкой прямоугольной щели,

распределение E

на которой принимается синусоидаль-

ным, входное сопротивление может быть с достаточной

для практики точностью определено по формулам:

z„-_ей£_

1Г

(«

с*4>

где /?

—

сопротивление излучения вибратора, пересчи-

танное к его входу [см. формулы (3-11) и

(3-14)];

р —

волновое сопротивление плоского вибратора,

вычисляемое по формуле (3-13), в которую

надо подставить эквивалентный радиус пло-

ского вибратора

*=\d\

(4-3)

здесь d—ширина пластины плоского вибратора, равная

ширине щели.

Резонансная длина щели, так же как и у вибратора,

несколько меньше половины длины волны.

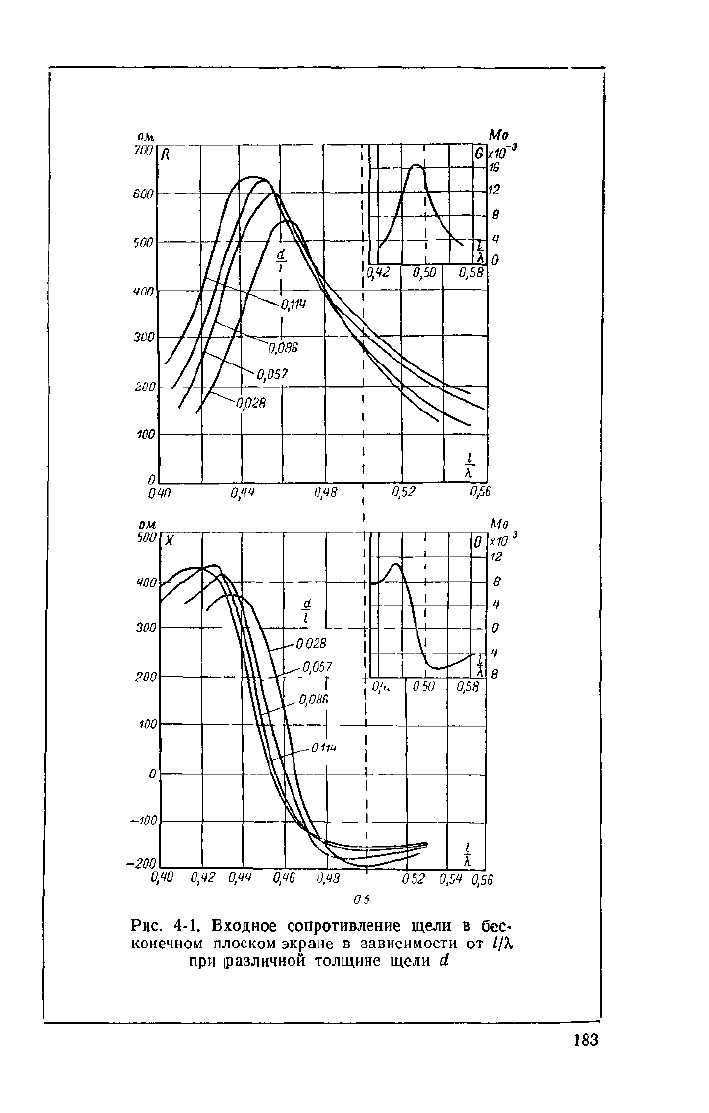
Экспериментальные кривые входного сопротивления

щели в плоском экране большого размера при различ-

ной ширине щели приведены на рис 4-1. В верхнем пра-

вом углу приведены для сравнения кривые проводимо-

стей бесконечно тонкого симметричного вибратора.

С увеличением толщины щели ее резонансная длина

уменьшается, входная проводимость падает, а полоса

пропускания растет. Для узких резонансных щелей мож-

но считать, что входное сопротивление равно.

ve3

{

^-~ 500 ом. (4-4)

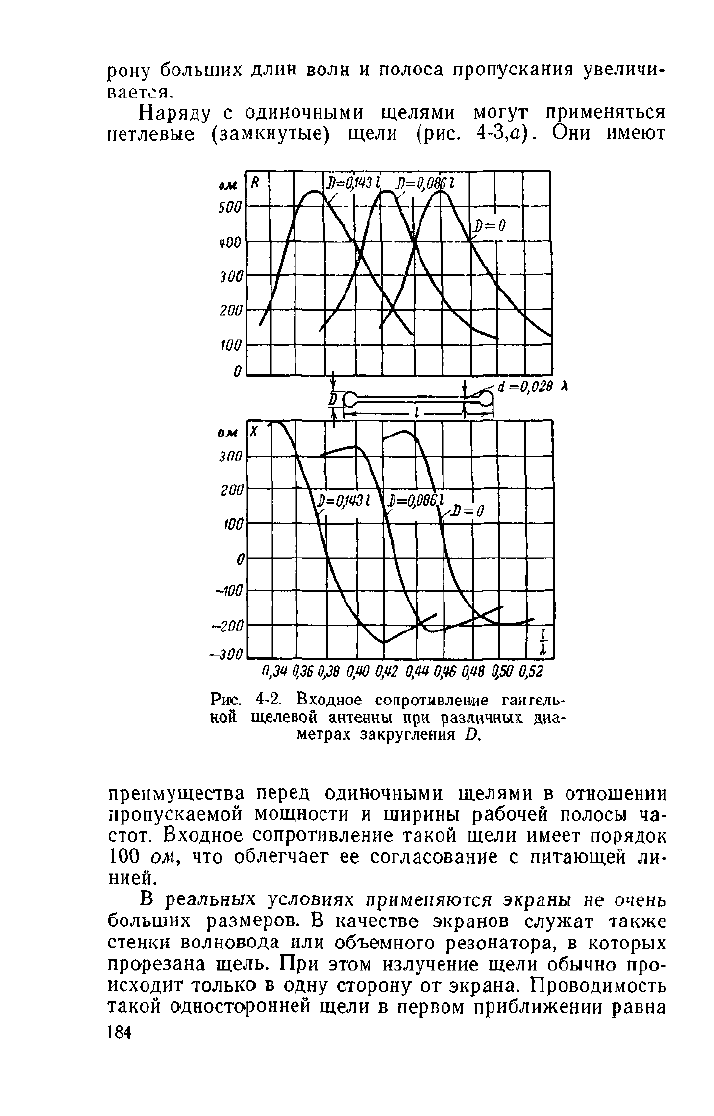
В случаях, когда излучатель должен быть более широ-

кополосным, находят применение гантельные щели. За-

висимость входного сопротивления от размеров для

такой щели приведена на рис. 4-2. С увеличением диа-

метра закругления D точка резонанса смещается в сто-

182

0,40 0,42 0,41 0,46 0,48 052 0,54 0,56

Рис.

4-1. Входное сопротивление щели в бес-

конечном плоском экране в зависимости от

1/Х

при различной толщине щели d

183

рону больших длин волн и полоса пропускания увеличи-

вается.

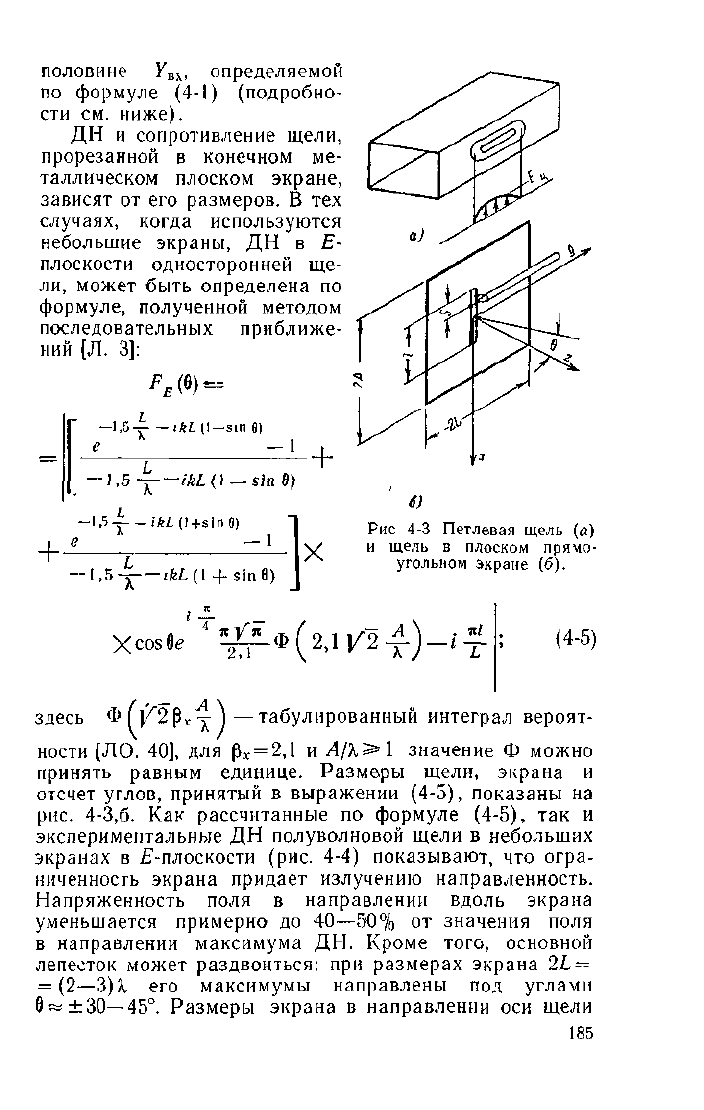
Наряду с одиночными щелями могут применяться

петлевые (замкнутые) щели (рис. 4-3,а). Они имеют

0,34

0,36

0,38

0,40

0,42

0,44

0,46

0,48

0,50

0,52

Рис.

4-2. Входное сопротивление ran

гель-

нон щелевой антенны при различных диа-

метрах закругления D.

преимущества перед одиночными щелями в отношении

пропускаемой мощности и ширины рабочей полосы ча-

стот. Входное сопротивление такой щели имеет порядок

100 ом, что облегчает ее согласование с питающей ли-

нией.

В реальных условиях применяются экраны не очень

больших размеров. В качестве экранов служат также

стенки волновода или объемного резонатора, в которых

прорезана щель. При этом излучение щели обычно про-

исходит только в одну сторону от экрана. Проводимость

такой односторонней щели в первом приближении равна

184

половине У

вх

, определяемой

по формуле (4-1) (подробно-

сти см. ниже).

ДН и сопротивление щели,

прорезанной в конечном ме-

таллическом плоском экране,

зависят от его размеров. В тех

случаях, когда используются

небольшие экраны, ДН в Е-

плоскости односторонней ще-

ли,

может быть определена по

формуле, полученной методом

последовательных приближе-

ний [Л. 3]:

— ikL (I —sin

—

1,5 -j-—ekL(l —sin 8)

-I.'S-j-

-IkLO+sln 0)

,5-jj-

ikL{\ +sin8)

Рис 4-3 Петлевая щель (a)

и щель в плоском прямо-

угольном экране (б).

X cos бе

7С

У~П

2,1

2,1/2-4)-/ 4

(4-5)

здесь

]/2

Рж

-у )—табулированный интеграл вероят-

ности [ЛО. 40], для

2,1

и Л/Я>1 значение Ф можно

принять равным единице. Размеры щели, экрана и

отсчет углов, принятый в выражении (4-5), показаны на

рис.

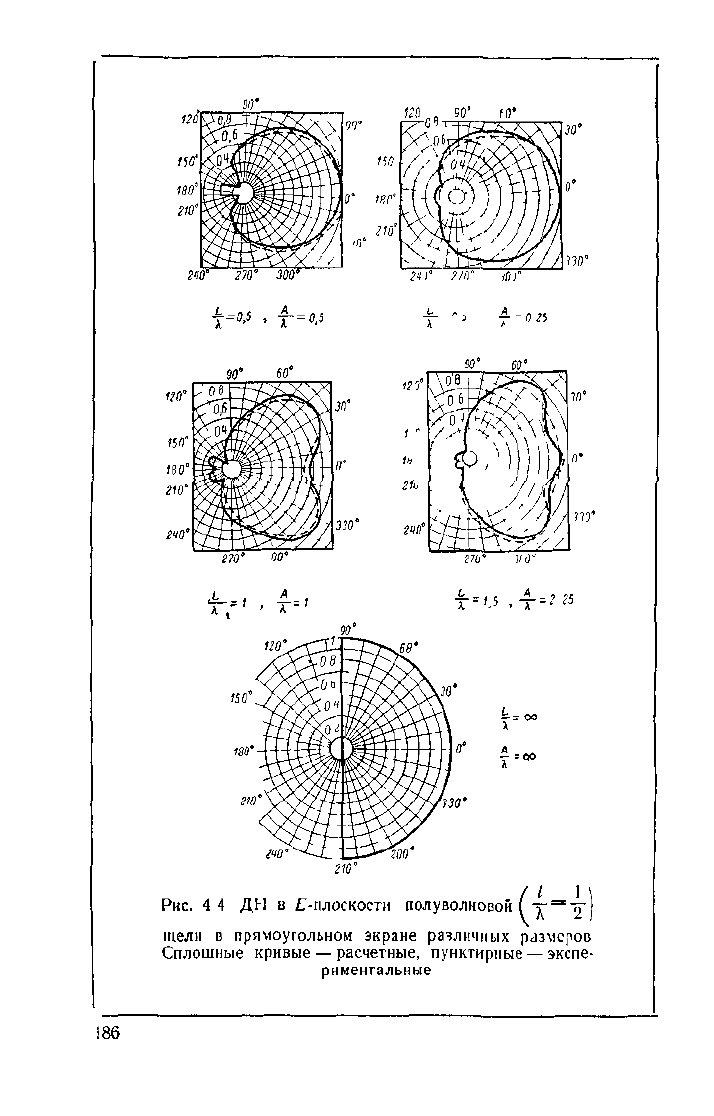
4-3,6. Как рассчитанные по формуле (4-5), так и

экспериментальные ДН полуволновой щели в небольших

экранах в ^-плоскости (рис. 4-4) показывают, что огра-

ниченность экрана придает излучению направленность.

Напряженность поля в направлении вдоль экрана

уменьшается примерно до 40—50% от значения поля

в направлении максимума ДН. Кроме того, основной

лепесток может раздвоиться: при размерах экрана

= (2—3)А, его максимумы направлены под углами

6— ±30—45°. Размеры экрана в направлении оси щели

185

120

150°

180

л|М

90°

SSyvyi

§9?/?<

кх/.с

гчо° 2?а° зоо°

{ = 0,5 , f

0,5

150

0° 1RP°

210°

iff

120

„„ SO' ff)'

30'

120°

150°

180°

210°

240°

90° 50°

^08

5хЬ

^S^KXsS

ШУ^йЛТ'

Jftl-jfJilT

Шш,

270° 00°

214° 110°

T='.5 >T = "

Ш°

Рис.

4 4 ДИ в Г-плоскости полуволновой ( Y

(к

щели в прямоугольном экране различных размеров

Сплошные кривые — расчетные, пунктирные

—

экспе-

риментальные

186

мало влияют на ДН как в ^-плоскости, так и в Я-пло-

скости.

ДН узкой щели длиной /, прорезанной в пластине

шириной а, могут быть также рассчитаны по выраже-

ниям, полученным в результате решения задачи о ди-

фракции плоской волны на бесконечном эллиптическом

цилиндре [Л. 4]. Тонкая пластина рассматривается как

предельный случай. При расположении щели параллель-

но оси пластины определяются ДН в ^-плоскости, а при

расположении щели перпендикулярно оси — в Я-пло-

скости. Формулы имеют вид:

для ^-плоскости

^(6) =

+ 2 K

Seu

n+l

)(ka,cosby, (4-6)

га=0

для //-плоскости

(Ы \ ы

cos -п~ cos 8 —cos -s-

*„(*)

—-

sin

(

1/2

+ Yj D

e2n

(ka, cos6)

\sinkf-^

xjX

я=0 0

[ ka,

X r , \-

> (4-7)

где S

(

n+i) (ka, cos

6) —

нечетная функция Матье (2/z+l)-ro

порядка;

ein

(ka,

cos

б) —

четная функция Матье 2п-го по-

рядка;

_ 2Al

{

X(ka, 0)

(ka,

0)C

ein

(ka, 0) '

H^l

{ka,

$) —

четная функция Матье—Ганкеля 2«-го по-

рядка;

187

/(2)

(ka, £)— нечетная функция Матье—Ганкеля

(2/7-f-

—j—

1)-го порядка; Шфих означает произ-

водную по 5;

А\

В\

п+1

— коэффициенты первых членов разложения

функций

егп

по cos

г8

(

(2n+l)

по

sin

гб

соответственно.

Таблицы функций Матье и значения А " и В"

приведены в [Л. 5]. Формулы (4-5)

—

(4-7) позволяют

рассчитать с достаточной для практики точностью ДН

щели, прорезанной в широкой стенке прямоугольного

волновода. Структура этих формул показывает, что поле

излучения состоит из двух слагаемых: поля излучения

щелевой антенны в бесконечном экране (щель в идеаль-

ных условиях) и поля токов, текущих по экрану.

Влияние малого экрана может быть использовано для

того,

чтобы получить ДН примерно одинаковой ширины

в обеих плоскостях; такую примерно осесимметричную

ДН имеет полуволновая щель, прорезанная в торце пря-

моугольного волновода и снабженная четвертьволно-

выми «карманами» (см. рис. 4-16,з).

При возбуждении щели коаксиальным кабелем

(рис.

4-3,6) для обеспечения его согласования с нагруз-

кой необходимо правильно выбрать точку питания.

Входное сопротивление в средних точках щели имеет по-

рядок 500 ом (4-4) а волновое сопротивление кабеля

50—75 ом. Поэтому точка питания должна быть сдви-

нута к краю щели; входное сопротивление уменьшается

примерно по закону sin

kS, оставаясь чисто активным.

Расстояние от края щели S подбирается так, чтобы

входное сопротивление в точках питания оказалось рав-

ным волновому сопротивлению кабеля. Для 50-омного

кабеля, например, и двусторонней щели S =

Входное сопротивление щели с односторонним излу-

чением зависит как от ее формы и размеров, так и от

данных полости, закрывающей щель с обратной сто-

роны. Полость оказывает также заметное влияние на

резонансную длину щели. Параметры односторонней

щели можно определить, рассматривая щель как неко-

торую длинную линию с эквивалентным коэффициентом

распространения у

и волновым сопротивлением р

[Л 6] Тогда входное сопротивление в средних точках

односторонней щели длиной 21 определится как

= 0,5p

tgYj

188

а резонансная длина 2/

рР

з~

0,5Ла, где

2я/уэ.

Если

полость имеет прямоугольную форму, то величины уо

и р

МОЖНО

найти из следующих выражений, получен-

ных Ю. К. Муравьевым:

I»

(

21п

дТ+Ч^

-ctg

£й

I/ ^™Г 4/ .

I Д \ | . М

(4-9)

где

ро

\ я

х{^

е = 2,718 ...;

Л—

глубина

—

ширина

Л —

ширина

["•£+'(•4-

[

"^+'(4)]

полости;

щели;

)]

-f

—

ctg Ли |

cos

(4-10)

где

JQ(X)—функция

Бесселя первого рода нулевого по-

рядка.

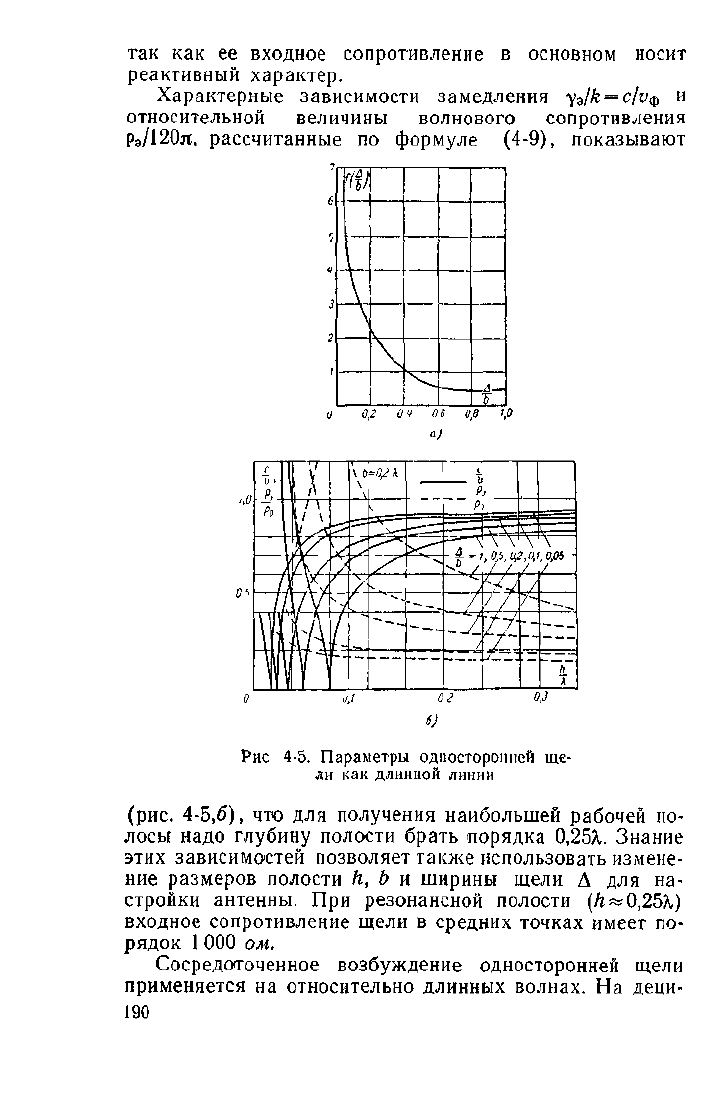
График функции !(А/Ь) приведен на рис. 4-5,я; фор-

мулы (4-9) и (4-10) являются приближенными; они

справедливы при относительно небольших размерах по-

лости, h^b, и при работе антенны в режиме стоячей

волны. Из них следует, что у

и р

будут действительны-

ми при выполнении условия

21n

E +

f(y)]>

(

)

При этом y

<k, т. е. фазовая скорость волны, рас-

пространяющейся вдоль щели, больше скорости света,

и 2/

ез>0,5А. При очень мелких полостях (&/г<1) усло-

вие (4-11) не выполняется; вдоль щели устанавливается

спадающее по экспоненте напряжение. Такая щель

плохо излучает и плохо согласуется с питающей линией,

189

так как ее входное сопротивление в основном носит

реактивный характер.

Характерные зависимости замедления

1к

с/иф

относительной величины волнового сопротивления

/120я, рассчитанные по формуле (4-9), показывают

I I I !

Рис 4-5. Параметры односторонней ще-

ли как длинной линии

(рис.

4-5,6), что для получения наибольшей рабочей по-

лосы надо глубину полости брать порядка 0,25Я. Знание

этих зависимостей позволяет также использовать измене-

ние размеров полости h, Ь и ширины щели А для на-

стройки антенны. При резонансной полости (/г»0,25Х)

входное сопротивление щели в средних точках имеет по-

рядок

000 ом.

Сосредоточенное возбуждение односторонней щели

применяется на относительно длинных волнах. На деци-

190