Zhu J. Applications of Fourier Transform to Smile Modeling: Theory and Implementation
Подождите немного. Документ загружается.


10.3 Lookback Options 241
L
2
=
1
2
+
1
π
∞
0
Re
f
2
(
φ
)
e
(1−i
φ
)z
1 −i
φ
+
e
i
φ
z
i
φ
d
φ
−
1
π
∞
0
z
−∞
Re
f
2
(
φ
)
e
i
φ
u
i
φ
+
sin(
φ
u)
φ
dud
φ
=
1
2
+
1
π
∞
0
Re
f
2
(
φ
)
e
(1−i
φ
)z
1 −i
φ
+
e
i
φ
z
i
φ
d
φ
+ lim
a→−∞
1
π
∞
0
Re
f
2
(
φ
)
e
i
φ
z
−e
i
φ
a
φ
2
−
cos(
φ
z) −cos(
φ
a)
φ
2
d
φ
.
(10.43)
The numerical integrals in (10.43) display a well-behaved and fast convergence
for a sufficiently small a,say−10.
4
The pricing formula for lookback options takes
then a form of
C
LB
= e
−rT
(F
T
0
−mL
1
−F
T
0
L
2
). (10.44)
The interpretation of this pricing formula is straightforward: L
1
is the probabil-
ity that the expected minimum up to maturity is smaller than the realized minimum
while L
2
gives the opposite probability but under another measure. The technique
applied in the above procedure is somehow different from anywhere else in this
book. We do not change measure to evaluate E
exp(m
X
T
) ·I
(m
X
T
z)
. Instead we cal-
culate it by using the density function.
If X(t) and r(t) follow the processes (10.20) and (10.21) respectively, we can
obtain a pricing formula for lookback options on spot in the same way,
C
LB
= E
exp
−
T
0
r(t)dt
S(T) −min(m,S
0
exp(m
X
T
)
= S
0
−B(0,T)(mL
1
+ S
0
L
2
) (10.45)
with
L
1
= Pr(m
X
T
> z)
=
1
2
+
1
π
∞
0
Re
f
2
(
φ
)
exp(−i
φ
z)
i
φ
d
φ
(10.46)
= e
−z
(
1−2v
−2
)
1
2
+
1
π
∞
0
Re
f
2
(
φ
)
exp(i
φ
z)
i
φ
d
φ
and
4
The number a = −10 for this intergral can be regarded to be sufficiently small because we have
m = 4.54×10
−5
F
T
0
(ln(m/F
T
0
)=−10) for this case and the probability Pr(m
X
T
−10) is actually
zero. Thus, we only need to implement the integral over the interval [a, z] instead of [−∞, z].

242 10 Exotic Options with Stochastic Volatilities
L
2
=
−1+2v
−2
4v
−2
e
2v
−2
z
+
1
π
∞
0
Re
f
2
(
φ
)
e
(1−i
φ
)z
1 −i
φ
+
1 −2v
−2
−i
φ
φ
2
−2v
−2
i
φ
e
(2v
−2
+i
φ
)z
d
φ
= e
2v
−2
z
[Pr(X(T) > −z) −0.25v
2
]
+
1
π
∞
0
Re
f
2
(
φ
)
e
(1−i
φ
)z
1 −i
φ
+
e
(2v
−2
+i
φ
)z
φ
2
−2v
−2
i
φ
d
φ
, (10.47)
where f
2
(
φ
) is defined by
f
2
(
φ
)=E
⎡
⎣
exp
−
T
0
r(t)dt
B(0,T)
exp(i
φ
X(T))
⎤
⎦
.
A similar procedure can be applied to price lookback put options. However, one
must know the probability distributions involving maximum. We have the following
proposition:
Proposition 10.3.1. (a): If X(t) follows the process (10.12) and the volatility v(t)
follows a mean-reverting Ornstein-Uhlenbeck process, and they are mutually not
correlated, then the probabilities of Pr(X(T) z
1
,M
X
T
y) and Pr(M
X
T
z
2
) with
z
1
z
2
and z
2
0 are respectively given by
Pr(X(T) z
1
,M
X
T
z
2
)
(10.48)
= e
z
2
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(−i
φ
(z
1
−2z
2
))
i
φ
d
φ
and
Pr(M
X
T
z
2
)=
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(−i
φ
z
2
)
i
φ
d
φ
(10.49)
− e
−z
2
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(i
φ
z
2
)
i
φ
d
φ
.
(b): If X(t) and r(t) follow the processes (10.20) and (10.21) respectively, then the
probabilities of Pr(X(T) z
1
,M
X
T
z
2
) and Pr(M
X
T
z
2
) with z
1
z
2
and z
2
0
are given by
Pr(X(T) z
1
,M
X
T
z
2
)
(10.50)
= e
−z
2
(
1−2v
−2
)
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(i
φ
(z
1
−2z
2
))
i
φ
d
φ

10.3 Lookback Options 243
and
Pr(M
X
T
z
2
)=
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(−i
φ
z
2
)
i
φ
d
φ
(10.51)
− e
−z
2
(
1−2v
−2
)
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(i
φ
z
2
)
i
φ
d
φ
.
A detailed proof is given in Appendix C. Since the terminal payoff of lookback
put options on futures is equal to max
t∈[0,T]
F
T
(t) −F
T
(T) , the corresponding the-
oretical prices can be evaluated by
P
LB
= e
−rT
E
maxF
T
(t) −F
T
(T)
= e
−rT
E
M Pr
M
X
T
z
+ F
T
0
exp(M
X
T
) ·I
(M
X
T
>z)
−F
T
(T)
= e
−rT
[M ·L
1
+ F
T
0
·L
2
−F
T
0
], (10.52)
where M is the realized maximum up to now and z is equal to ln(M/F
T
0
). L
1
and L
2
are respectively given by
L
1
=
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(−i
φ
z)
i
φ
d
φ
− e
−z
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(i
φ
z)
i
φ
d
φ
and
L
2
= E[exp(M
X
T
) ·I
(M
X
T
>z)
]
=
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(i
φ
z)
i
φ
d
φ
+ lim
a→∞
1
π
∞
0
Re
f
2
(
φ
)
e
(1−i
φ
)a
−e
(1−i
φ
)z
1 −i
φ
d
φ
+ lim
a→∞
1
π
∞
0
Re
f
2
(
φ
)
e
i
φ
a
−e
i
φ
z
φ
2
−
cos(
φ
a) −cos(
φ
z)
φ
2
d
φ
.
In a practical implementation, setting the number a as 10 offers us very accurate
results. The last integral in L
2
converges faster at a quadratic rate of
φ
. The deriva-
tion of the pricing formula for lookback put options on spot follows an analogous
way,
P
LB
= B(0,T )[M ·L
1
+ S
0
·L
1
] −S
0
(10.53)
with

244 10 Exotic Options with Stochastic Volatilities
L
1
=
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(−i
φ
z)
i
φ
d
φ
− e
−z
(
1−2v
−2
)
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(i
φ
z)
i
φ
d
φ
and
L
2
= lim
a→∞
1
π
∞
0
Re
f
2
(
φ
)
e
(1−i
φ
)a
−e
(1−i
φ
)z
1 −i
φ
d
φ
+
1
1 −b
lim
a→∞
1
π
∞
0
Re
⎛
⎝
f
2
(
φ
)
e
(1−b+i
φ
)a
−e
(1−b+i
φ
)z
1 −b + i
φ
⎞
⎠
d
φ
−
b
1 −b
e
(1−b)z
1
2
−
1
π
∞
0
Re
f
2
(
φ
)
exp(i
φ
z)
i
φ
d
φ
,
where b = 1 −2v
−2
. With these complex pricing formulas having been derived, we
close this section.
10.4 Asian Options
10.4.1 Introduction
Asian options are referred to as a class of options whose payoff at maturity depends
on a certain average of some prices of the underlying asset prior to the expiration.
The average designed in a contract could be arithmetic or geometric. Asian options
based on an arithmetic average dominate trading in the OTC markets. The exotic
average feature of Asian options is especially designed for those thinly traded assets
whose prices can be manipulated easily. Hence, the average component in Asian
options allows their holders to control the risk of manipulation better. Another us-
age of Asian options, which is not emphasized in the literature, is the diversification
of volatile market prices. In this section, we study the effect of stochastic volatili-
ties on the pricing of Asian options and give closed-form pricing formulas for two
cases: a mean-reverting Ornstein-Uhlenbeck process and a mean-reverting square-
root process. This is a natural extension of our modular pricing by using the Fourier
transform. An Asian option is usually cheaper than its standard counterpart. Thus,
it is also an economic alternative for hedging and other risk management.
A still unsolved problem in financial economics is that one can not find a closed-
form solution for arithmetic average Asian options even in the Black-Scholes world.
However, the closed-form solution for Asian options with a geometric average is
available since the geometric average of stock prices is still lognormally distributed.
If the time to maturity of an option has the same length as the average period spec-
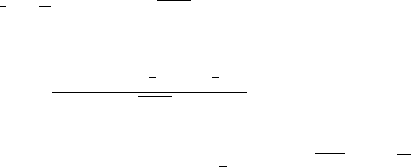
10.4 Asian Options 245
ified in the option contract, we have the following formula for Asian options with
continuous geometric average:
C
asian
= S
0
e
−(
1
2
rT+
1
12
v
2
T)
N(d +
T/3v) −Ke
−rT
N(d), (10.54)
where
d =
ln(S
0
/K)+
1
2
T(r −
1
2
v
2
)
T/3v
.
In comparison with the Black-Scholes formula for standard options, this formula
has two additional correction terms: 1/2forT(r −
1
2
v
2
) and
1/3for
√
Tv.This
is the reason why Asian options are cheaper than their standard counterparts. In
the following subsections, at first, we explain how these two terms enter the valua-
tion formula. Next, we incorporate stochastic factors including random jumps into
the pricing formulas. The third subsection is about the approximation methods for
arithmetic average Asian options. Finally, we deal with a pricing model for Asian
interest rate options.
10.4.2 The Black-Scholes World
In this subsection, we give an alternative pricing formula to (10.54) by applying the
Fourier inversion. This formula is equivalent to the existing one. The purpose of
giving an alternative pricing formula, which, at first glance, is more complicated, is
twofold. Firstly, we show why hedging with Asian options is different from hedging
with plain vanilla options. In other words, why we need to modify the method of
risk-neutral pricing used for plain vanilla options. Secondly, we make preparations
for the valuation of Asian options with stochastic factors. Some notations are defined
here:
• n
0
: the number of total observation points in the whole average period.
• n : the number of remaining observation points for calculating the average stock
price. For out-of-the-period (OTP) Asian options we have n
0
= n.
• T
0
: time from the current time to the first observation point. For in-the-period
(ITP) or at-the-period (ATP) Asian options T
0
= 0.
• h : observation frequency defined by the whole average period dividing n.
Instead of using the arithmetic average, we use the geometric average of the ob-
served stock prices to price Asian options. The discrete geometric average is defined
as follows:
GA(n)=
n
∏
j=1
S
j
1/n
. (10.55)
where S
j
is the stock price at the j-th observation point. The price of an Asian option
is then generally given by
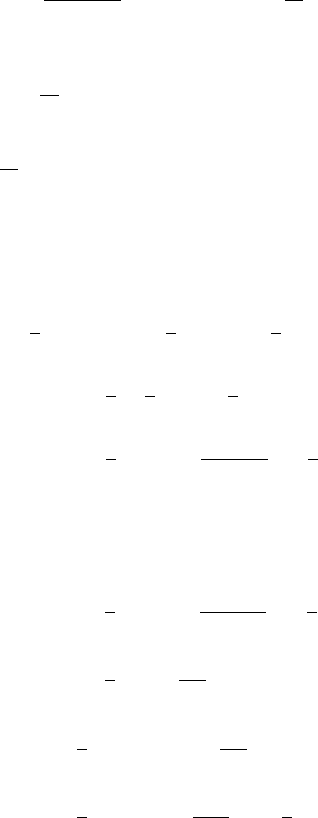
246 10 Exotic Options with Stochastic Volatilities
C
asian
= e
−rT
E
{(nGA(n)+A)/n
0
−K}·1
{nGA(n)+AK·n
0
}
(10.56)
= e
−rT
E
{(nGA(n)+A)/n
0
−K}·1
{GA(n)(K·n
0
−A)/n}
,
where A is the sum of stock prices from the first day of the average period to the
current time, and is equal to zero for the OTP- and ATP-Asian options.
Defining
K
0
=
K ·n
0
−A
n
and K
1
= K −
A
n
0
, (10.57)
we have
C
asian
= e
−rT
E
n
n
0
GA(n) −K
1
·1
{GA(n)K
0
}
(10.58)
= e
−rT
n
n
0
E
GA(n) ·1
{GA(n)K
0
}
−e
−rT
K
1
E
1
{GA(n)K
0
}
.
What we need to do is calculating the CFs of GA(n) under the risk-neutral mea-
sure. We consider the Black-Scholes world where the volatility is constant. The
logarithm of GA(n) can be expanded as follows:
lnGA(n)=
1
n
ln
n
∏
j=1
S
j
=
1
n
n
∑
j=1
lnS
j
=
1
n
n
∑
j=1
x
j
= x
0
+(r −
1
2
v
2
)
1
n
n
∑
j=1
T
j
+
v
n
n
∑
j=1
W
j
= x
0
+(r −
1
2
v
2
)
T
0
+
h(n +1)
2
+
v
n
n
∑
j=1
W
j
. (10.59)
So we have
E[exp(i
φ
lnGA(n)]
= E
exp
i
φ
x
0
+(r −
1
2
v
2
)
T
0
+
h(n +1)
2
+
v
n
n
∑
j=1
W
j
= E
exp
i
φ
x
0
+ i
φ
(r −
1
2
v
2
)t
1
+
i
φ
v
n
n
∑
j=1
W
j
= exp
i
φ
x
0
+ i
φ
(r −
1
2
v
2
)t
1
E
exp
i
φ
v
n
n
∑
j=1
W
j
= exp
i
φ
x
0
+ i
φ
(r −
1
2
v
2
)t
1
exp
−
φ
2
2
Var
v
n
n
∑
j=1
W
j
(10.60)
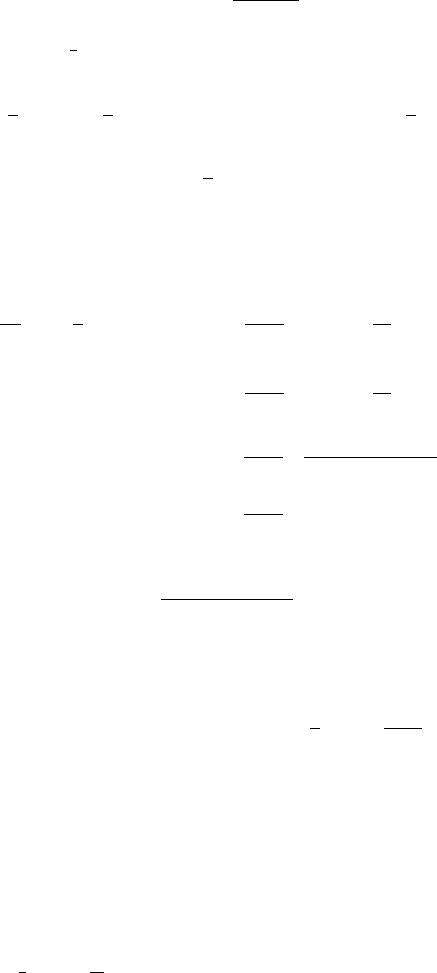
10.4 Asian Options 247
with
t
1
= T
0
+
h(n +1)
2
.
To calculate Var
v
n
∑
n
j=1
W
j
, the following equation
1
n
n
∑
j=1
W
j
=
1
n
n
∑
j=1
(W(T
0
)+ j
Δ
W
j
)=W(T
0
)+
n
∑
j=1
j
n
Δ
W
j
= W (T
0
)+
n
∑
j=1
j
n
W(h)
is the key to the following calculation. Due to the Markovian property of the Brow-
nian motion we immediately obtain
exp
φ
2
2
Var
v
n
n
∑
j=1
W
j
= exp
v
2
φ
2
2
T
0
+
n
∑
j=1
j
2
n
2
h
= exp
v
2
φ
2
2
T
0
+
n
∑
j=1
j
2
n
2
h
= exp
v
2
φ
2
2
h(n +1)(2n + 1)
6n
+ T
0
= exp
v
2
φ
2
2
t
2
,
where
t
2
=
h(n +1)(2n + 1)
6n
+ T
0
.
Therefore we have
f
2
(
φ
;lnGA(n)) = E[exp(i
φ
lnGA(n)]
= exp
i
φ
x
0
+ i
φ
(r −
1
2
v
2
)t
1
−
v
2
φ
2
2
t
2
. (10.61)
Now we consider the following expected value,
E
GA(n) ·1
{GA(n)K
0
}
.
In order to guarantee the risk-neutral pricing and a suitable hedging, we have
to find a suitable process M(t) such that GA(n)/S
0
M(t) is a likelihood process
with an expected value of one. M(t)=e
rt
, usually suggested for standard op-
tions, obviously can no longer satisfy the required condition since E[GA(n)] =
exp
x
0
+(r −
1
2
v
2
)t
1
+
v
2
2
t
2
. This means that the usual arbitrage argument for Eu-
ropean options is no longer valid for Asian options. An appropriate M(t) should
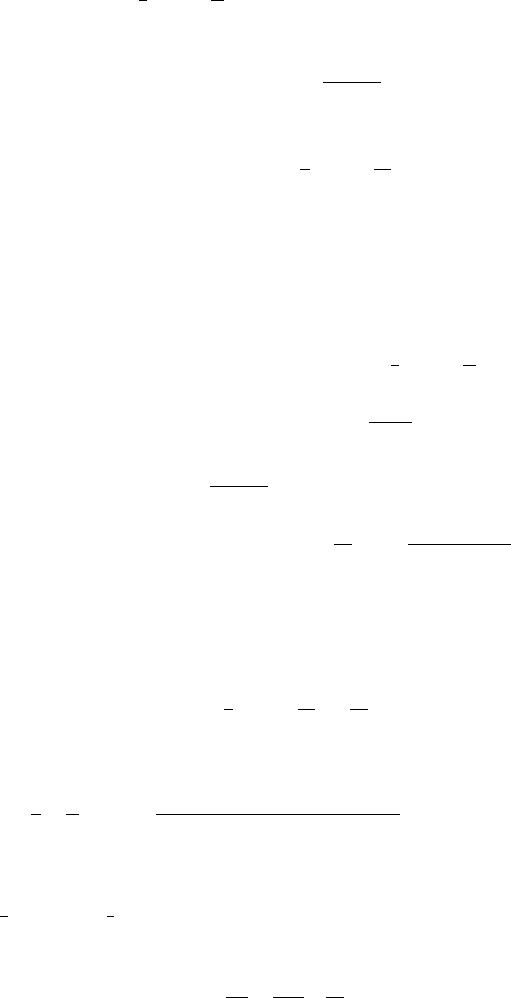
248 10 Exotic Options with Stochastic Volatilities
be the term exp
(r −
1
2
v
2
)t
1
+
v
2
2
t
2
, with which we have E[GA(n)/S
0
M(t)] = 1.
Thus,
E
GA(n) ·I
{GA(n)K
0
}
= S
0
M(t)E
GA(n)
S
0
M(t)
·I
{GA(n)K
0
}
(10.62)
with
M(t)=exp
(r −
1
2
v
2
)t
1
+
v
2
2
t
2
.
The expectation in the above equality implies a probability measure due to the spe-
cial term S
0
M(t). It is well worth discussing M(t) in more detail because it includes
some useful information for hedging. Due to the correlation among the sequence
of stock prices, t
2
is somehow smaller than t
1
and M(t) can not be reduced to e
rt
.
Hence, the volatility v plays an important role in discounting GA(n) to S
0
, which
is not the case for plain vanilla options. The larger the volatility v is, the smaller
the value of the “discounted” spot price S
0
exp
(r −
1
2
v
2
)t
1
+
v
2
2
t
2
is. This effect
shows the usefulness and effectiveness of Asian options in eliminating the undesired
impact of volatility on option prices. The CF of E
GA(n)
S
0
M(t)
·1
{GA(n)K
0
}
is given by
f
1
(
φ
;lnGA(n)) = E
GA(n)
S
0
M(t)
exp(i
φ
lnGA(n)
= exp
i
φ
x
0
+ i
φ
r −
i
φ
2
v
2
t
1
+
v
2
(2i
φ
−
φ
2
)
2
t
2
.
(10.63)
Hence, the pricing formula for Asian stock options with the discrete geometric
average may be given by
C
asian
= exp
−rT +(r −
1
2
v
2
)t
1
+
v
2
2
t
2
n
n
0
S
0
F
1
−e
−rT
K
1
F
2
. (10.64)
where
F
j
=
1
2
+
1
π
∞
0
Re
f
j
(
φ
;lnGA(n))exp(−i
φ
lnK
0
)
i
φ
d
φ
, j = 1,2. (10.65)
If n approaches infinity, we actually arrive at the pricing formula for options
with the continuous geometric average. In the case of ATP-Asian options, we have
t
1
=
1
2
T and t
2
=
1
3
T. Consequently, the pricing formula for Asian options with a
continuous geometric average is given by
C
asian
= exp
−
rT
2
−
v
2
T
12
n
n
0
S
0
F
1
−e
−rT
K
1
F
2
, (10.66)
which is identical to formula (10.54).
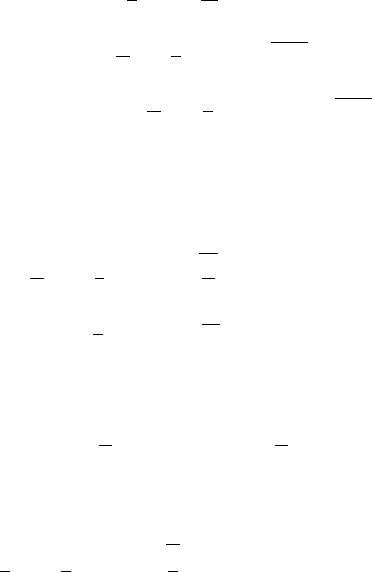
10.4 Asian Options 249
10.4.3 Asian Options in a Stochastic World
In this subsection, we take stochastic volatilities and stochastic interest rates into
account in pricing geometric average Asian options. Intuitively, lnGA(n) should
follow a Brownian motion since GA(n) is lognormally distributed. In order to ob-
tain the concrete form of the process of lnGA(n), we consider E[GA(n)].Fromthe
results in the above subsection, we rewrite
E[GA(n)] = E[exp(lnGA(n)]
= exp
x
0
+(r −
1
2
v
2
)t
1
+
v
2
2
t
2
= E
exp
x
0
+
t
1
T
(r −
1
2
v
2
)T +(
t
2
/Tv)W
T
= E
exp
x
0
+
T
0
t
1
T
(r −
1
2
v
2
)dt +
T
0
(
t
2
/Tv)dW
.
(10.67)
This expression with stochastic integral implies a “visual” stochastic process of
lnGA(n), which takes the following form
d lnGA(t;n)=
t
1
T
r −
1
2
v
2
dt +
t
2
T
vdW,
=
ε
1
r −
1
2
v
2
dt +(
√
ε
2
v)dW, lnGA(0;n)=x
0
,
(10.68)
with
ε
1
=
t
1
T
, and
ε
2
=
t
2
T
.
In the case of ATP-Asian options with infinity n, t
1
/T = 1/2 and t
1
/T = 1/3.
The process can be rewritten as
d lnGA(t)=
1
2
r −
1
2
v
2
dt +
1
3
vdW, lnGA(0;n)=x
0
. (10.69)
We call such a process of lnGA(t) “visual” since this process can not be directly ob-
served in the marketplaces and is derived from the stock price process. The deriva-
tion of the rigorous process of GA(t;n) in the presence of stochastic volatilities and
interest rates is mathematically very cumbersome and does not result in a tractable
form. To incorporate stochastic factors into geometric average Asian options, we
have the following assumption:
Assumption: The geometric average of n sequential stock prices of Asian op-
tions GA(t;n) follows the process (10.68) even in the presence of stochastic volatil-
ities and stochastic interest rates.
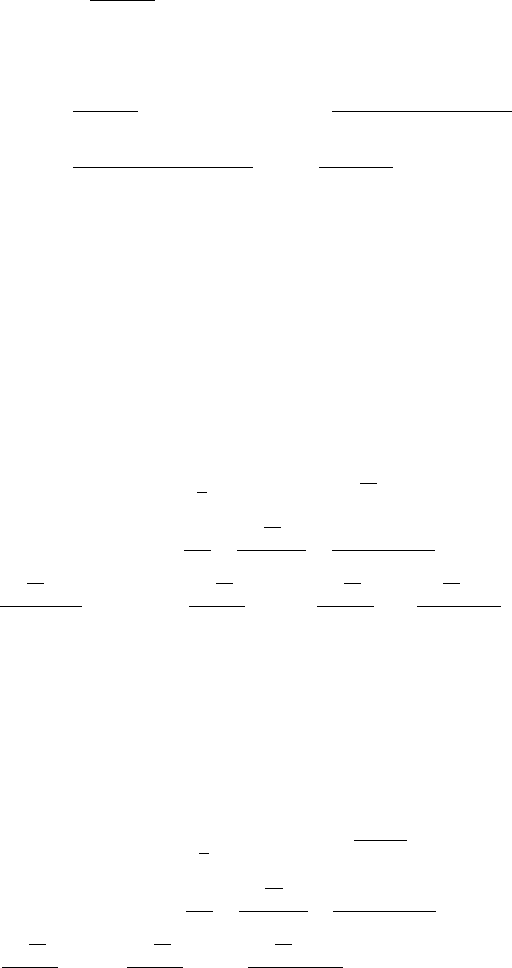
250 10 Exotic Options with Stochastic Volatilities
If the pricing formula for Asian options implies no arbitrage, as mentioned above,
then there exists a process M(t) such that the following equation holds,
E
GA(T)
S
0
M(T )
= 1 ⇐⇒ M(T)=E[GA(T )]/S
0
. (10.70)
Consequently, the CFs f
1
(
φ
) and f
2
(
φ
) are given by
f
1
(
φ
)=E
GA(n)
S
0
M(T )
exp(i
φ
lnGA(n)
= E
exp((1 + i
φ
)lnGA(n))
S
0
M(T )
= E
exp((1 + i
φ
)lnGA(n))
E[GA(T)]
= E
g(1 +i
φ
)
E[g(1)]
(10.71)
and
f
2
(
φ
)=E[g(i
φ
)], (10.72)
where the function g(a)=exp(alnGA(n)). Again, in order to calculate the CFs, we
classify the volatilities in two popular cases.
Case 1: A mean-reverting Ornstein-Uhlenbeck process.
Similar to the Sch
¨
obel and Zhu (1999) model, we may compute the following
expected value,
E[g(a)]
= E[exp(alnGA(n))]
= E
exp
ax
0
+ a
T
0
ε
1
(r −
1
2
v(t)
2
)dt +a
T
0
(
√
ε
2
v(t))dW (t)
= E
exp
ax
0
+ a
ε
1
rT −
a
ε
1
2
−
a
√
ε
2
ρκ
σ
−
a
2
ε
2
(1−
ρ
2
)
2
T
0
v
2
(t)dt
−
a
√
ε
2
ρκθ
σ
T
0
v(t)dt +
a
√
ε
2
ρ
2
σ
v
2
(T) −
a
√
ε
2
ρ
2
σ
v
2
0
−
a
√
ε
2
ρσ
T
2
.
(10.73)
Case 2: A mean-reverting square-root process.
As in the Heston (1993) model, computing the following expected value is
straightforward,
E[g(a)]
= E[exp(alnGA(n))]
= E
exp
ax
0
+ a
T
0
ε
1
(r −
1
2
V(t)dt + a
T
0
(
ε
2
V(t))dW(t)
= E
exp
ax
0
+ a
ε
1
rT −
a
ε
1
2
−
a
√
ε
2
ρκ
σ
−
a
2
ε
2
(1−
ρ
2
)
2
T
0
V(t)dt
+
a
√
ε
2
ρ
σ
V(T ) −
a
√
ε
2
ρ
σ
V(0) −
a
√
ε
2
ρκθ
T
σ
. (10.74)
