Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

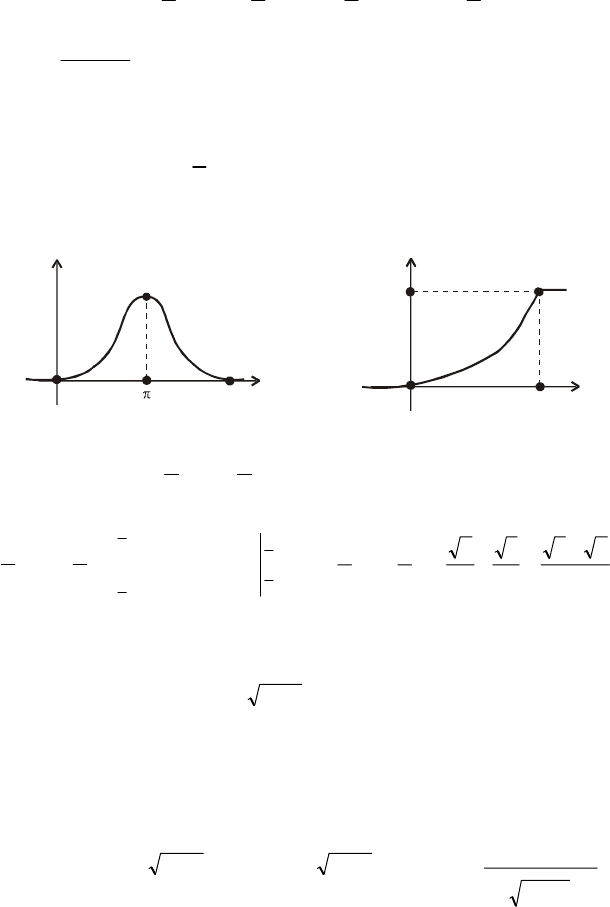
88
Розв’язання. Згідно із (74) маємо:
.
2
cos1
)1cos(
2
1
)|cos(
2
1
sin
2
1
sin
2
1
)()(
0
000
x
xxdxdxdxxfxF
x
xxx
−
=
=+−=−====
∫∫∫
Отже, функція розподілу ймовірностей буде така:
()
⎪
⎪
⎩
⎪
⎪
⎨
⎧
π>
π≤<−
≤
=
.,1
;0),cos1(
2
1
;0,0
x
xx
x
xF
Графіки функцій f (x), F(x) зображені відповідно на рис. 29 і 30.
2
π
F x
()
0
x
π
f x
()
0
x
π
2
–
Рис. 29 Рис. 30
Імовірність події
26
π
<<
π
X
можна обчислити згідно з (65) або (72).
Застосуємо формулу (72):
.
2
23
2
3
2
2
6
cos
4
coscos
46
2
6
4
6
−
=+−=
π
+
π
−=−==
⎟
⎠
⎞
⎜
⎝
⎛
π
<<
π
∫
π
π
π
π
xdxxXP sіn
Приклад 3. За заданою щільністю ймовірностей маємо:
⎪
⎩
⎪
⎨
⎧
>
≤<−+
−≤
=
.7,0
;72,2
;2,0
)(
x
xxa
x
xf
Знайти значення сталої а та функцію F(x). Побудувати гра-
фіки функцій f (x), F(x).
Розв’язання. Значення сталої а визначаємо з умови нормування (71):
.
2
1
12121)(
7
2
7
2
7
2
7
2
dxx
adxxadxxadxxf
+
=→=+→=+→=
∫
∫∫∫
−
−−−
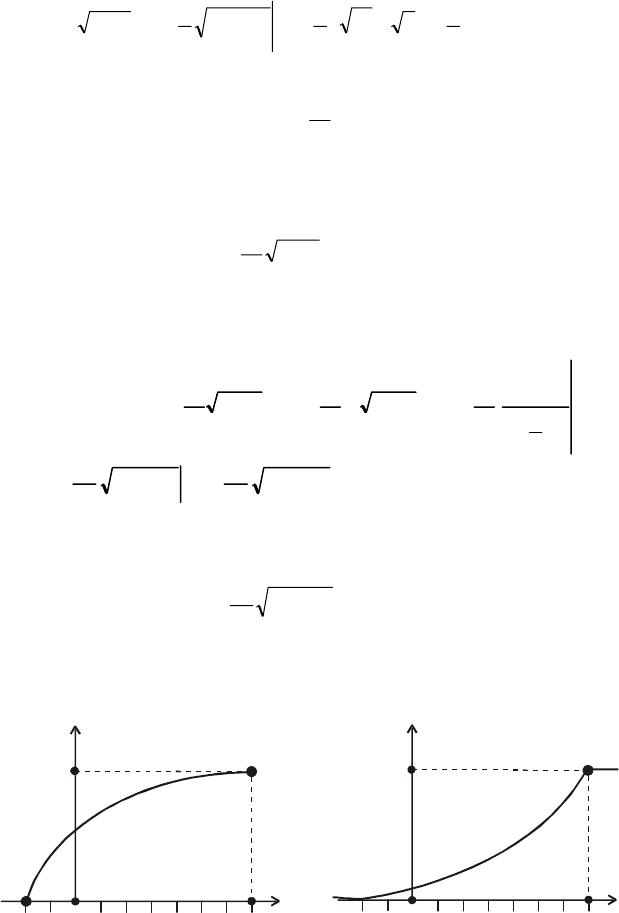
89
Тут
.1827
3
2
09
3
2
)2(
3
2
2
3
7
2
3
7
2
==
⎟
⎠
⎞
⎜
⎝
⎛
−=+=+
−
−
∫
xdxx
Отже,
.
18
1
=a
При знайденому значенні а щільність імовірностей
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−+
−≤
=
.7,0
;72,2
18
1
;2,0
)(
x
xx
x
xf
Функція розподілу ймовірностей визначається так:
.)2(
27
1
)2(
27
1
2
3
)2(
18
1
2
18
1
2
18
1
)()(
3
2
3
2
3
222
+=+=
=
+
=+=+==
−
−
−−−
∫∫∫
xx
x
dxxdxxdxxfxF
x
x
xxx
Отже,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−+
−≤
=
.7,1
;72,)2(
27
1
;2,0
)(
3
x
xx
x
xF
Графіки функцій f (x), F(x) зображені відповідно на рис. 31 і 32.
f
x
()
1
–
2 0 7
x
(7; 1/6)
Fx
()
1
–
2 0 7
x
Рис. 31 Рис. 32
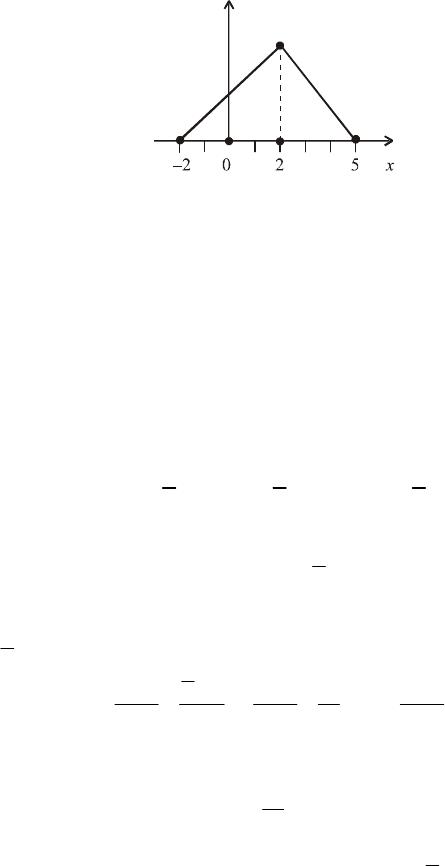
90
Приклад 4. Неперервна випадкова величина Х має закон ро-
зподілу ймовірностей у вигляді трикутника, зображеного на
рис. 33.
f
x
()
СКВ
Ау
(2; )
Рис. 33
Записати вирази для щільності ймовірностей і функції роз-
поділу ймовірностей. Побудувати графік F(x) і обчислити
Р(0 < X < 4).
Розв’язання. На проміжку [–2; 2] щільність імовірностей змінюєть-
ся за законом прямої пропорційної залежності f (x) = k
1
x + b
1
(k
1
> 0), а
на проміжку [2; 5] за аналогічним законом f (x) = k
2
x + b
2
(k
2
< 0). Для
знаходження значень параметрів k
1
, b
1
, k
2
, b
2
обчислимо координати ве-
ршини цього трикутника А(х, у). Абсциса цієї точки відома за умовою
задачі: х = 2; ординату знаходимо за умовою нормування, згідно з якою
площа цього трикутника АВС має дорівнювати одиниці:
.
7
2
17
2
1
2
1
=→==⋅=
∆
yyAKCBS
Отже, шукані координати:
.
7
2
;2 == уx
Знаходимо рівняння прямої, яка проходить через точки С (–2; 0) і
⎟
⎠
⎞
⎜
⎝
⎛
7
2
;2A
:
Отже, на проміжку [–2; 2] маємо:
).2(
14
1
)( += xxf
Рівняння прямої, що проходить через точки
()
0;2,
7
2
;2
BA
⎟
⎠
⎞
⎜
⎝
⎛
:
.
14
2
14
1
222
0
7
2
2
0 +
=→=
+
→
+
−
=
+
− x
y
x
y
x
y
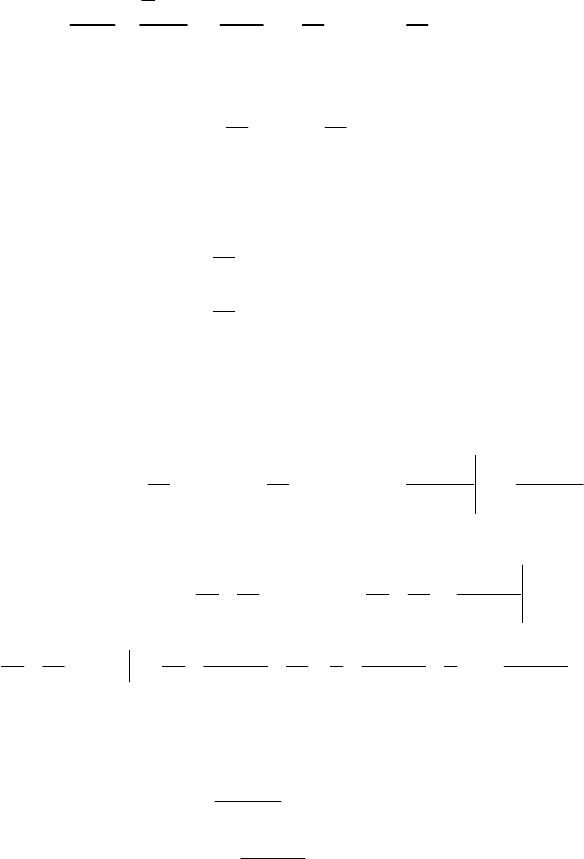
91
).5(
21
2
21
2
552
0
7
2
5
0
−−=→−=
−
→
−
−
=
−
−
xy
x
y
x
y
Звідси на проміжку [2; 5] дістаємо:
).5(
21
2
)5(
21
2
)( xxxf −=−−=
Отже, на проміжку [–2; 5] щільність імовірностей
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<−
≤<−+
−≤
=
.5,0
;52),5(
21
2
;22),2(
14
1
;2,0
)(
x
xx
xx
x
xf
Згідно із (74) знаходимо F(x) на обох розглядуваних проміжках:
1) на проміжку [–2; 2]:
;
28
)2(
28
)2(
)2(
14
1
)2(
14
1
)()(
2
2
2
2
22
+
=
+
=+=+==
−
−−−
∫∫∫
xx
dxxdxxdxxfxF
x
xxx
2) на проміжку [–2; 5]:
.
21
)5(
1
7
3
21
)5(
7
4
21
9
21
)5(
28
16
)5(
21
1
28
16
2
)5(
21
1
28
16
)5(
21
2
28
16
)()2()(
222
2
2
2
2
22
−
−=−
−
−=+
−
−=−−=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−+=−+=+=
−
∫∫
xxx
x
x
dxxdxxfFxF
x
x
xx
Отже, функція розподілу ймовірностей
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
−
−
≤<−
+
−≤
=
.5,1
;52,
21
)5(
1
;22,
28
)2(
;2,0
)(
2
2
x
x
x
x
x
x
xF
Графік F(x) зображено на рис. 34.
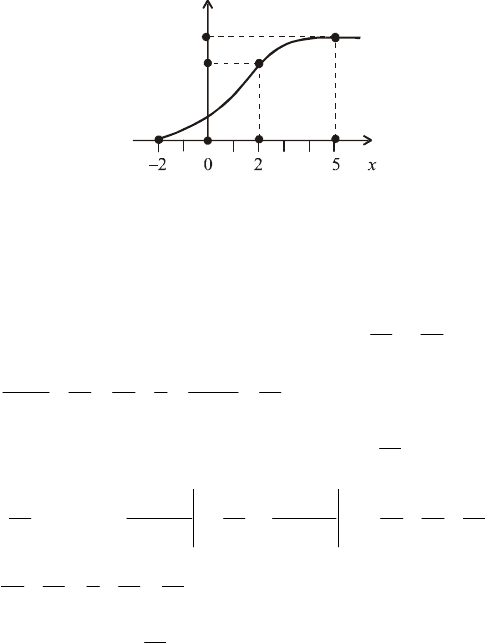
92
7
4
Fx
()
1
7
4
–
Рис. 34
Обчислюємо ймовірність події 0 < X < 4 згідно з (65) і (72).
На інтервалі [0; 4] діють два закони розподілу:
1)
.
21
17
21
320
7
1
21
20
28
4
21
121
28
4
21
1
1)0()4()2()4()0()2(
).42()20()40(
=
−
=−=−
−
=
=−
⎟
⎠
⎞
⎜
⎝
⎛
−=−=−+−
<
<
+
<
<
=<<
FFFFFF
XPXPXP
.
21
17
21
8
7
3
21
8
28
12
)91(
21
1
28
4
28
16
2
)5(
21
2
28
)2(
)5(
21
2
)2(
14
1
)42()20()40()2
4
2
2
2
0
2
4
2
2
0
=+=+=
=+−+−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−+
+
=−+
++=<<+<<=<<
∫
∫
xx
dxx
dxxXPXPXP
Отже,
()
21
17
40 =<< XP
.
Теоретичні запитання до теми
?
1. Означення випадкової величини.
2. Означення дискретної і неперервної випадкової величини.
3. Умова нормування для дискретної випадкової величини.
4. Закон розподілу випадкової величини.
5. Що називається функцією розподілу випадкової величини?
6. Довести, що
(
)
)(
12
xFxF ≥
при x
2
> x
1
.
7. Чому дорівнює
)(),(
∞
∞
−
FF
?
8. Чому дорівнює
)(
β
<
<
α
XP
?
9. Довести, що для неперервної випадкової величини
Р (Х = х) = ...

93
10. Означення щільності ймовірностей неперервної випад-
кової величини Х.
11. Чому дорівнює
∫
∞
∞−
dxxf )(
?
12. Чому дорівнює
∫
β
α
dxxf )(
?
13. Чому дорівнює
∫
∞−
x
dxxf )(
?
14. Якщо Х ∈ [a; b], то чому дорівнює
∫
b
а
dxxf )(
?
15. Якщо Х ∈ [а; b], то чому дорівнює
∫
x
a
dxxf )(
?
16. Властивості F(x).
17. Властивості f (x).
18. Довести, що
∫
∞−
=
x
xFdxxf )()(
.
Приклади до теми
1. За заданим законом розподілу дискретної випадкової величи-
ни Х маємо:
Х = х
і
– 4 –1 2 5 8 10
Р(Х = х
і
) = р
і
а 1,5а 0,5а 3,5а 2,5а а
Знайти а. Обчислити: P(X < 2), P(– 4 < X
≤
8).
Побудувати функцію розподілу ймовірностей і накреслити її
графік.
Відповідь. а = 0,1; 0,25; 0,8.
2. За заданою функцією розподілу ймовірностей
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
≤<
≤<−
−≤<−
−≤
=<=
8,1
;85,8,0
;52,5,0
;21,3,0
;14,1,0
;4,0
)()(
x
x
x
x
x
x
xXPxF
обчислити:
).2();5();2();24(
≤
≥>
≤
<− XPXPXPXP
Відповідь: 0,5; 0,5; 0,5; 0,5.
94
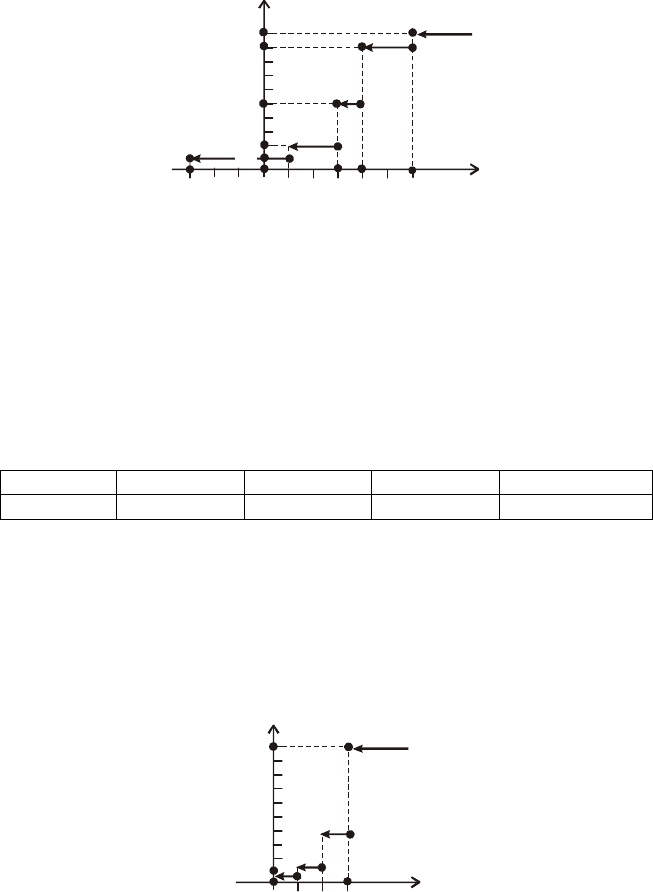
3. Дано функцію розподілу ймовірностей (рис. 35).
–
3 0 1 3 4 6
х
Fx
()
1
0,1
0,5
0,9
Рис. 35
Обчислити:
()
(
)
(
)
.3;61;3 ≥
<
≤
≤ XPXPXP
Відповідь: 0,5; 0,4; 0,7.
4. Троє складають іспит із теорії ймовірностей. Імовірність того,
що перший студент складе екзамен, становить 0,9, для другого та
третього студентів ця ймовірність дорівнює відповідно 0,85; 0,8.
Побудувати закон розподілу ймовірностей дискретної випадкової
величини Х — числа студентів, які складуть іспит з теорії ймовірнос-
тей, побудувати F(x) і накреслити її графік.
Відповідь.
х
і
0 1 2 3
р
і
0,003 0,056 0,329 0,612
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
≤<
≤<
≤
=
.3,1
;32,398,0
;20,059,0
;10,003,0
;0,0
)(
x
x
x
x
x
xF
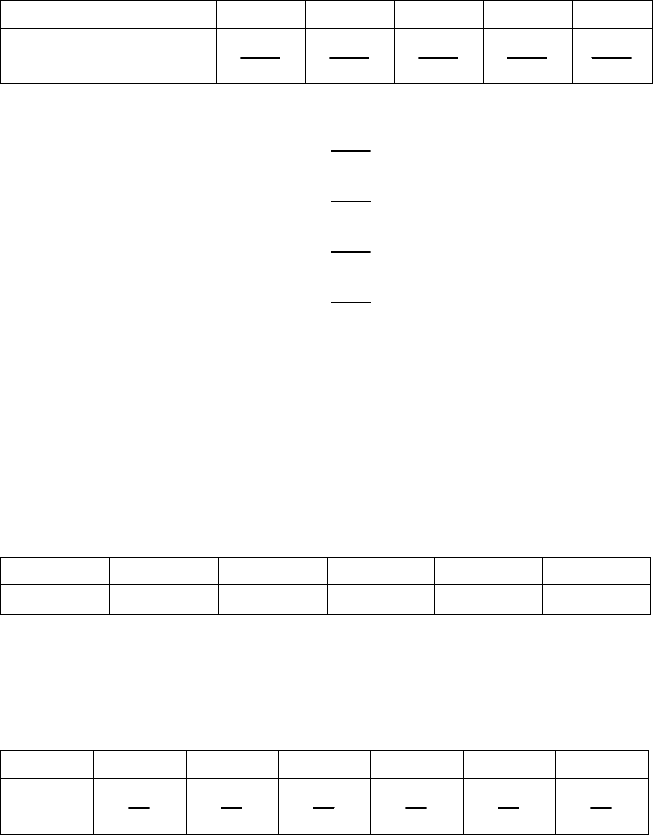
Графік F(x) зображено на рис. 36
0 1 2 3
х
Fx
()
1
0,1
Рис. 36
95
5. У першому ящику міститься 7 стандартних і 3 браковані деталі, у
другому — 6 стандартних і 4 браковані. Навмання з першого ящика бе-
руть чотири деталі, а з другого — одну. Побудувати закон розподілу
ймовірностей дискретної випадкової величини Х — появи числа стан-
дартних деталей серед чотирьох навмання взятих — і побудувати F(x).
Відповідь.
х
і
1 2 3 4 5
р
і
2100
28
2100
294
2100
798
2100
770
2100
210
⎪
⎪
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
≤<
≤<
≤<
≤
=<=
.5,1
;54,
2100
1890
;43,
2100
1120
;32,
2100
322
;21,
2100
28
;1,0
)()(
x
x
x
x
x
x
xXPxF
6. Під час виготовлення деталі робітникові необхідно виконати
чотири незалежні між собою технологічні операції. Імовірність того,
що при виконанні першої операції робітник не припуститься дефекту,
дорівнює 0,95; для другої, третьої і четвертої операцій ця ймовір-
ність становить відповідно 0,9; 0,85; 0,8. Побудувати закон розподі-
лу дискретної випадкової величини Х — числа операції, під час ви-
конання
яких робітник не припуститься браку.
Відповідь.
х
і
0 1 2 3 4
р
і
0,00015 0,00565 0,06965 0,34315 0,5814
7. На шляху руху автомобіля стоять п’ять світлофорів, кожний із
яких з імовірністю 0,5 дозволяє або забороняє рух. Побудувати за-
кон розподілу ймовірностей дискретної випадкової Х — числа світ-
лофорів, що їх автомобіль промине без затримки.
Відповідь.
х
і
0 1 2 3 4 5
р
і
32
1
32
5
32
10
32
10
32
5
32
1

96
8. Імовірність того, що футболіст реалізує одинадцятиметровий
штрафний удар дорівнює 0,9. Футболіст виконав три такі удари.
Побудувати закон розподілу ймовірностей дискретної випадкової
величини Х — числа реалізованих штрафних.
Відповідь.
х
і
0 1 2 3
р
і
0,001 0,027 0,243 0,729
9. П’ять приладів потрібно перевірити на надійність. Кожний
наступний прилад підлягає перeвірці лише в тому разі, якщо пе-
ревірений прилад перед цим виявляється надійним. Імовірність
того, що прилад витримає перевірку на надійність, для кожного
з них дорівнює 0,8. Побудувати закон розподілу дискретної ви-
падкової величини Х — числа приладів, які пройшли
випро-
бування.
Відповідь.
х
і
1 2 3 4 5
р
і
0,2 0,16 0,128 0,1024 0,4096
10. У лотереї розігруються мотоцикл, велосипед і годинник.
Усього є 100 лотерейних білетів. Навмання покупець придбав один з
них. Побудувати закон розподілу ймовірностей Х — поява виграш-
ного білета.
Відповідь.
х
і
0 1 1 1
р
і
0,97 0,01 0,01 0,01
11. За заданою функцією розподілу ймовірностей неперервної
випадкової величини Х
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
+
−≤
=
1,1
;13,
2
3
;3,0
)(
x
x
x
x
xF
побудувати її графік і обчислити P(–2 < X < 0).
Відповідь. Шуканий графік наведено на рис. 37.
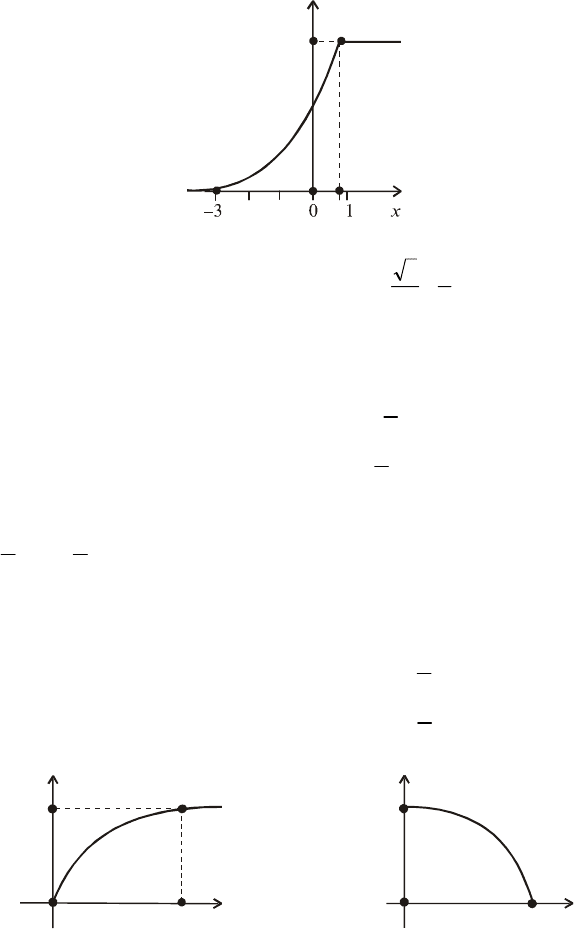
97
Fx
()
1
Рис. 37
.
2
1
2
3
)2()0()02( −=−−+<<− FFXP
12. Задано функцію розподілу ймовірностей
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
π
>
π
≤<
≤
=
.
2
,1
;
2
0,sin
;0,0
)(
x
xx
x
xF
Знайти f (x). Побудувати графіки F(x), f(x) і обчислити
⎟
⎠
⎞
⎜
⎝
⎛
π
<<
π
36
XP
.
Відповідь.
2
π
Fx
()
0
x
2
π
1
–
2
π
2
π
f
x
()
0
x
–
Рис. 38 Рис. 39
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
π
>
π
≤<
≤
=
′
=
.
2
,0
;
2
0,cos
;0,0
)()(
x
xx
x
xFxf
