Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

58
Згідно з (35) для досить великого числа спроб n маємо наближе-
ну рівність:
m
x
xx
mjіn
xxmmmP
i
im
∆ϕ≈≤≤
∑
=
)()( ,
де
npqnpq
npm
npq
npm
xxx
mmm
11
1
=
−
−
−+
=−=∆
+
;
2
2
2
1
)(
m
x
m
ex
−
π
=ϕ
.
Отже, можна записати:
∑
=
ϕ
π
≈≤≤
j
im
x
xx
m
jin
npq
x
mmmP
)(
2
1
)(
. (46)
Тут (46) є інтегральною сумою, а тому
=
π
=
ϕ
π
=≤≤
∫
∑
−
=
∞→∞→
dxe
npq
x
mmmP
j
i
j
іm
x
x
x
x
xx
m
n
jіn
n
2
2
2
1
)(
2
1
)(
limlim
()
()
.ФФ
2
1
2
1
2
1
2
1
0
2
0
2
0
2
0
2
2222
ij
x
x
x
x
x
x
x
x
xх
dxedxedxedxe
i
j
i
і
−=
=
π
−
π
=
π
+
π
=
∫∫∫∫
−−−−
Для великих, але обмежених значень n дістанемо:
)(Ф)(Ф)(
іjjіn
xхmmmP
−
≈≤
≤
, що й потрібно було довести.
Властивості функції Лапласа
1. Ф(x) визначена на всій осі абсцис.
2. Ф(–x) = – Ф(x), отже, Ф(x) є непарною функцією.
3. Ф(0) = 0.
4.
()
5,0
2
1
Ф
0
2
2
=
π
=∞
∫
∞
−
dxe
x
, оскільки π=
∫
∞
∞−
−
2
2
2
dxe
x
є інтегралом
Пуассона.
5. Ф(–
5,0)Ф( −=−∞ , як непарна функція.
6.
()
0
2
1
Ф
2
2
>
π
=
′
−
x
eх , отже, Ф (х) є функцією неспадною.
7. Ф"(0) = 0;
.x;xФ
xx
0)(Ф0)(
00
<
′′
>
′′
<<
Таким чином, x = 0 є точкою перегину.
Графік функції Ф(х) зображено на рис. 17
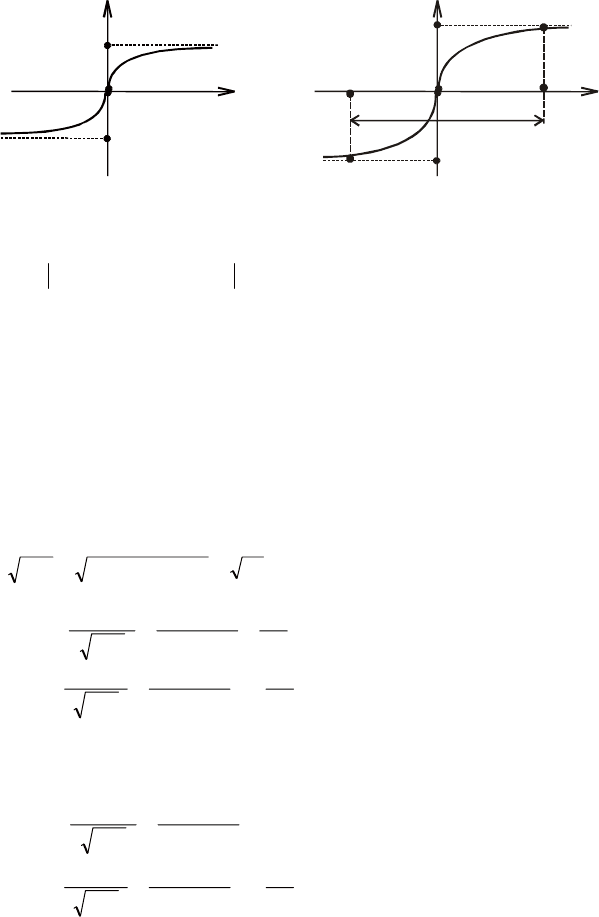
59
0,5
0
х
–0,5
Ф ()
х
0,5
4–4
0 –4 4
≤≤
хх
–0,5
Ф ()
х
Рис. 17 Рис. 18
Розв’язуючи задачі, додержують такого правила:
5,0)Ф(
4
≈
≥х
x , 5,0)Ф(
4
≈
−≤х
x .
Отже, практично функція Лапласа застосовується для значень
[]
4;4−∈x , що ілюструє рис. 18.
Приклад 1. Верстат-автомат виготовляє однотипні деталі.
Імовірність того, що виготовлена одна деталь виявиться ста-
ндартною, є величиною сталою і дорівнює 0,95. За зміну вер-
статом було виготовлено 800 деталей. Яка ймовірність того,
що стандартних деталей серед них буде: 1) від 720 до 780
шт.; 2) від 740 до 790 шт.?
Розв’язання. За умовою задачі:
800=n ;
95,0=p
;
05,0
=
q
; 780720
≤
≤
m ; 780740
≤
≤
m ;
76095,0800,2,63805,095,0800 =⋅=≈=⋅⋅= npnpq .
1)
23,3
2,6
20
2,6
760780
≈=
−
=
−
=
npq
npm
x
j
j
;
5,6
2,6
40
2,6
760720
−≈−=
−
=
−
=
npq
npm
x
і
і
;
;99931,05,049931,0
)5,6Ф()23,3Ф()5,6Ф()23,3Ф()780720(
800
=+=
=+=−−≈≤≤ mP
2)
84,4
2,6
760790
≈
−
=
−
=
npq
npm
x
j
j
;
23,3
2,6
20
2,6
760740
−≈−=
−
=
−
=
npq
npm
x
i
i
;
.99931,031499,05,0
)23,3Ф()84,4Ф()23,3Ф()84,4Ф()790740(
800
=⋅+=
=+=−−≈≤≤= mP
60
Приклад 2. В електромережу ввімкнено незалежно одну від
одної 500 електролампочок, які освітлюють у вечірній час
виробничий цех заводу. Імовірність того, що електролампо-
чка в електромережі не перегорить, є величиною сталою і
дорівнює 0,8. Яка ймовірність того, що з 500 електролампо-
чок не перегорить:
1) не більш як 380 шт.;
2) не менш як 390 шт.
Розв’
язання. За умовою задачі:
500=n ; 8,0=p ; 2,0=q ; 3800
≤
≤
m ; 500390
≤
≤
m ;
.4008,0500,9,8802,08,0500 =⋅=≈=⋅⋅= npnpq
1)
;25,2
9,8
20
9,8
400380
9,8
4003809
−≈−=
−
−=
−
=
−
=
npq
npm
x
j
j
45
9,8
4000
−≈
−
=
−
=
npq
npm
x
i
i
;
.0119,04881,05,0
)25,2Ф()5,4Ф()45Ф()25,2Ф()3800(
500
=−=
=
−
=
−
−
−
≈
≤≤= mP
2)
12,1
9,8
10
9,8
400390
−≈−=
−
=
−
=
npq
npm
x
i
i
;
23,11
9,8
100
9,8
400500
≈=
−
=
−
=
npq
npm
x
j
j
;
.8686,03686,05,0
)12,1Ф()23,11Ф()12,1;1Ф()23,11Ф()400390(
500
=+=
=+=−−≈≤≤ mP
5. Використання інтегральної теореми
За допомогою (45) можна оцінити близькість відносної частоти
W(А) до ймовірності p випадкової події А. Нехай p — імовірність
появи випадкової події А в кожному експерименті за схемою Бернул-
лі й W(А) — відносна частота появи цієї події при n експериментах.
Необхідно оцінити ймовірність події ⎮W(A) – р
⎮< ε (ε > 0 і є ма-
лою величиною). Якщо n набуває великих значень, то можна за фо-
рмулою (45) дістати:
Р(|W(A) – p| < ε) =
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε<
−
<ε−=
⎟
⎠
⎞
⎜
⎝
⎛
ε<
−
<ε−=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε<−=
hq
n
npq
npm
pq
n
P
n
npm
Pp
n
m
P

61
=
π
−
π
=
π
=
∫∫∫
ε−
−
ε
−
ε
ε−
−
dxedxedxe
pq
n
x
рq
т
x
pq
n
pq
n
x
0
2
0
22
2
1
2
1
2
1
222
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε
pq
n
pq
n
pq
n
nq
n
ФФФФ
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε=
pq
n
pq
n
Ф2Ф2
.
Отже,
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε=ε<−
pq
n
pAWP Ф2)|)((|
. (46а)
Приклад 1. Імовірність виходу з ладу виробу під час прове-
дення експерименту, який має на меті виявити надійність
виробу в роботі, дорівнює 0,2. Було перевірено 400 виробів.
Чому дорівнює ймовірність такої події: абсолютна величина
відхилення відносної частоти виходу із ладу виробів від
імовірності p = 0,2 становить ε = 0,01?
Розв’язання. За умовою задачі: n = 400; p
= 0,2; q = 0,8; ε = 0,01. Пі-
дставивши ці значення в (46), дістанемо:
.383,01915,02)5,0Ф(2
8,02,0
400
01,0Ф2)01,0|2,0)((| =⋅==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
⋅
≈<−AWP
Приклад 2. У разі автоматичного виготовлення втулок брак
становить у середньому 10%. Скільки втулок має взяти кон-
тролер, аби ймовірність того, що абсолютна величина від-
хилення відносної частоти появи стандартної втулки W(A)
(А — випадкова подія, що полягає в появі стандартної втул-
ки) від імовірності p виготовлення такої втулки не переви-
щує ε = 0,001, дорівнювала 0,999:
999,0)|)((|
≈
ε
<
−
pAWP .
Розв’язання. За умовою задачі: q = 0,1, ε = 0,001, p = 1 – q = 1 – 0,1 =
= 0,9;
999,0)001,0|9,0)((|
≈
<
−
AWP .
Далі маємо:
,999,0)Ф(2Ф2)|)((| ==
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε=ε<− x
pq
n
pAWP
62
.де
2
pq
x
n
pq
n
x
⎟
⎠
⎞
⎜
⎝
⎛
ε
=→ε=
Оскільки 2Ф(x) = 0,999, то Ф(x) = 0,4995 → x ≈ 3,4 (див. дод. 2).
Отже,
104040009,0)3400(1,09,0
001,0
4,3
2
2
==⋅
⎟
⎠
⎞
⎜
⎝
⎛
=n
.
Тобто контролер має перевірити 1 040 400 втулок.
Приклад 3. Імовірність появи випадкової події в кожному з
900 незалежних експериментів є величиною сталою і дорівнює
0,75. Яким має бути значення ε > 0, щоб P(|W(A) – p| < ε) =
= 0,99?
Розв’язання. За умовою задачі: n = 900; p = 0,75; q = 0,25;
2Ф(x) = 0,99.
Далі маємо Ф(x) = 0,495; x = 2,74 і
x = ε
04,0
30
25,075,074,2
25,075,0
900
74,2
≈
⋅
=
⋅
==ε→
pq
n
x
pq
n
.
Отже, умову задачі задовольняє значення ε ≈ 0,04.
6. Формула Пуассона для малоймовірних
випадкових подій
Точність асимптотичних формул для великих значень n — числа
повторних незалежних експериментів за схемою Бернуллі — знижу-
ється з наближенням p до нуля. Тому при
,
∞
→n
0→p
за умови
np = a = const імовірність появи випадкової події m раз
)0( nm ≤≤
обчислюється за такою асимптотичною формулою:
a
m
n
m
a
mP
−
≈ e
!
)(
, (47)
яка називається формулою Пуассона.
Доведення. Оскільки а = np, то
n
a
pq
n
a
p −=−== 11,
.
Запишемо формулу Бернуллі у такому вигляді:
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
==
−
−
mnm
m
m
n
mnmm
nn
n
a
n
a
P
A
qpCmP 1)(
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
+−−−
=
−mm
n
a
n
a
m
mnnnn
1
!
)1(...)2()1(
!
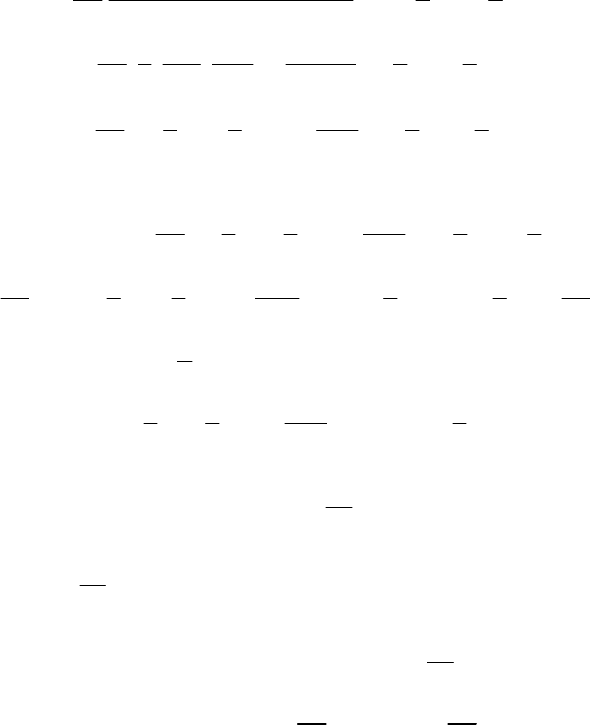
63
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
+−−−
=
−mn
m
m
n
a
n
a
n
mnnnn
m
a
11
)1(...)2()1(
!
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
+−−−
=
−mn
m
n
a
n
a
n
mn
n
n
n
n
n
n
m
a
11
1
...
21
!
.11
1
1...
2
1
1
1
!
mn
m
n
a
n
a
n
m
nnm
a
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−=
Коли
∞→n , дістаємо:
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−=
−
∞→∞
mn
m
n
n
n
n
a
n
a
n
m
nnm
a
mP 11
1
1...
2
1
1
1
!
lim)(lim
a
m
m
n
n
nn
m
e
m
a
n
a
n
a
n
m
nnm
a
−
−
∞→∞→∞→
=
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−=
!
1lim1lim
1
1...
2
1
1
1lim
!
.
Оскільки
a
n
n
e
n
a
−
∞→
=
⎟
⎠
⎞
⎜
⎝
⎛
−1lim
,
11lim;1
1
1...
2
1
1
1lim =
⎟
⎠
⎞
⎜
⎝
⎛
−=
⎟
⎠
⎞
⎜
⎝
⎛
−
−
⎟
⎠
⎞
⎜
⎝
⎛
−
⎟
⎠
⎞
⎜
⎝
⎛
−
−
∞→∞→
m
nn
n
a
n
m
nn
.
Отже,
a
m
n
n
e
m
a
mP
−
→∞
=
!
)(lim
,
а для великих, але обмежених значень n маємо:
a
m
n
e
m
a
mP
−
≈
!
)( , що й потрібно було довести.
Із (47) випливає:
a
m
m
mm
m
mm
njіn
e
m
a
mPmmmP
j
s
j
і
−
==
∑∑
==≤≤
!
)()( ; (48)
1
!!
)()0(
000
=====≤≤
−
=
−−
==
∑∑∑
aa
m
n
m
aa
m
n
m
n
m
nn
ee
m
a
ee
m
a
mPnmP .
І справді, це підтверджується ще й тим, що події
nm
≤
≤
0 утворю-
ють повну групу.
Функція Р
n
(m) визначається за таблицею, наведеною в дод. 3, за
заданим m і обчисленим значенням а = np.
Приклад 1. Радіоприлад містить 1000 мікроелементів, які
працюють незалежно один від одного, причому кожний мо-
же вийти з ладу під час роботи приладу з імовірністю р =
= 0,002. Обчислити ймовірності таких випадкових подій:

64
1) під час роботи приладу з ладу вийдуть 3 мікроелементи;
2) від трьох до шести.
Розв’язання. За умовою задачі маємо n = 1000; p = 0,002; m = 3;
3
6≤≤ m . Оскільки n велике, а р мале число, то для обчислення ймовір-
ностей застосуємо формули (47) і (48). Для цього обчислимо значення
параметра а = np = 1000 · 0,002 = 2.
1)
18044,0)3(
1000
≈P .
2)
=
+
+
+
=≤≤ )6()5()4()3()63(
10001000100010001000
PPPPmP
=
.,,,,,, 52131002160400504090100819016803101804470
=
+
+
+
+
Приклад 2. Імовірність того, що під час епідемії грипу ме-
шканець міста захворіє на цю хворобу, становить у серед-
ньому 0,03%. Яка ймовірність того, що серед навмання виб-
раних 300 мешканців міста хворих на грип виявиться:
1) 5 осіб; 2) не більш як 3 особи.
Розв’язання. За умовою: p = 0,003; n = 300; m = 5;
.30
≤
≤
m
Обчислюємо значення параметра а = np = 300 ⋅ 0,003 = 0,9.
1) P
800
(5)
≈
0,002001.
2)
=
+
+
+
=≤≤ )3()2()1()0()30(
300300300300300
PPPPmP
.,,,,, 9965420049398016466103659130406570
=
+
+
+=
Теоретичні запитання до теми
?
1. Які експерименти називають експериментами за схемою
Бернуллі?
2. За якої умови формула Бернуллі застосовується для обчи-
слення ймовірностей?
3. Що називають найімовірнішим числом (модою)?
4. Довести, що
pnpmqnp
+
≤
≤
−
0
.
5. Чому дорівнює
mnmm
n
n
m
qpC
−
=
∑
0
?
6. Сформулювати локальну теорему Муавра—Лапласа.
7. Сформулювати інтегральну теорему Муавра—Лапласа.
8. Чому дорівнює
)|)((|
ε
<
−
pAWP ?
9. Функція Гаусса та її властивості.
10. Функція Лапласа та її властивості.
11. За якої умови використовується формула Пуассона?
12. Чому дорівнює
a
m
n
m
e
m
a
−
=
∑
!
0
?
65
13. Записати формулу Пуассона для малоймовірних випад-
кових подій.
14. Асимптотичні формули для обчислення ймовірностей
випадкових подій для n незалежних експериментів за схе-
мою Бернуллі.
15. Чому дорівнює
)Ф(lim х
x +∞→
?
16. Чому дорівнює
)Ф(lim х
x −∞→
?
17. Чому дорівнює
∫
∞
∞−
−
π
dxe
x
2
2
2
1
?
18. Застосовуючи формулу Стірлінга, записати, чому дорів-
нює k!.
19. Чому дорівнює
)(lim x
x
ϕ
±∞→
?
20. Довести, що
()
()
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
ε=ε<−
pq
n
pAWP Ф2
.
21. Довести, що
a
m
n
e
m
a
mP
−
=
!
)( .
22. Довести, що ).Ф()Ф()(
іjJіn
хxmmmP
−
≈
≤
≤
Приклади до теми
1. Під час тестування з математики студент має дати правильні
відповіді на 5 запитань. Імовірність того, що він на позитивну оцін-
ку відповість на одне запитання, у середньому дорівнює 0,8. Щоб
скласти тест, студентові необхідно дати відповідь не менш ніж на
три питання. Знайти ймовірність того, що студент складе тест.
Відповідь. 0,84208.
2. Садівником восени було посаджено сім саджанців яблуні. Імо-
вірність того, що будь-який із саджанців навесні проросте, у серед-
ньому складає 0,7. Обчислити ймовірність того, що із семи саджан-
ців яблуні навесні проростуть: 1) три саджанці; 2) не менш як три.
Знайти найімовірніше число саджанців, які навесні проростуть, і об-
числити відповідну
ймовірність.
Відповідь. 1) 0,0416745; 2) 0,0693983; m
0
= 5; Р
7
(5) = 0,3176523.
3. Імовірність виготовлення робітником деталі відмінної якості
становить 0,75. Яка ймовірність того, що серед 6 виготовлених дета-
лей робітником хоча б одна буде відмінної якості? Знайти найімовір-
ніше число виготовлених робітником деталей відмінної якості й об-
числити ймовірність цього числа.
Відповідь. 0,9997559; m
0
= 5; Р
6
(5)
≈
0,3559569.

66
4. Робітник обслуговує 10 верстатів-автоматів. Імовірність того,
що верстат потребує уваги робітника протягом однієї години в серед-
ньому складає 0,6. Знайти ймовірність того, що за 1 годину уваги
робітника потребують: 1) 4 верстати; 2) від 4 до 6 верстатів (урахо-
вуючи межі). Знайти найімовірніше число m
0
верстатів, які потре-
бують уваги робітника за 1 год і обчислити ймовірність цього числа.
Відповідь. 1) 0,1114767; 2) 0,5619574; m
0
= 6; Р
10
(6)
≈
0,2508226.
5. На автобазі є 12 пасажирських автобусів. Імовірність того, що
на маршрутну лінію вийде автобус, у середньому дорівнює 0,85.
Знайти ймовірність того, що автобаза працюватиме в нормальному
режимі, якщо для цього потрібно, аби на маршрутну лінію виїхало
не менш як 9 автобусів.
Відповідь. 0,6871141.
6. У разі ввімкнення запалювання мотор автомобіля почне пра-
цювати з
імовірністю 0,99. Яка ймовірність того, що: 1) мотор почне
працювати при двох увімкненнях запалювання; 2) не більш як двох.
Відповідь. 1) 0,9801; 2) 0,9999.
7. По військовому кораблю здійснюють три постріли з ракетної
батареї системи «земля—земля». Імовірність влучити в корабель до-
рівнює 0,95, а ймовірність того, що військовий корабель буде знеш-
коджений, дорівнює 1 – q
k
, де k — число влучень ракет у корабель.
Обчислити ймовірність того, що корабель буде знешкоджений.
Відповідь.
=−+−+−+−= )1()1()1()1(
030
3
21
3
222
3
333
3
qqCqpqCqqpCqpCP
.9991799,0=
8. Завод виготовляє однотипні телевізори, з яких 85% вищої якос-
ті. Із партії виготовлених заводом телевізорів навмання вибирають
сім. Яка ймовірність того, що серед них телевізорів вищої якості бу-
де: 1) 4; 2) не менш як 4.
Відповідь. 1) 0,0178821; 2) 0,8509384.
9. У партії однотипних деталей кількості стандартних і бракова-
них деталей відносяться, як 5 : 2. Навмання з партії беруть 8 дета
-
лей. Яка ймовірність того, що серед них стандартних виявиться 6?
Знайти найімовірніше число появи стандартних деталей серед семи
навмання взятих і обчислити відповідну ймовірність.
Відповідь.
823543
500000
)6(;6;
823543
500000
80
≈= Pm .
10. У кожному із семи ящиків міститься по 6 стандартних і 4
браковані однотипні деталі. Навмання з кожного ящика беруть по
одній деталі. Обчислити ймовірність того, що серед семи взятих де-
талей стандартних буде: 1) 3; 2) не менш як 3; 3) не більш як 3.
Відповідь. 1) 0,193536; 2) 0,9811584; 3) 0,096256.

67
11. Імовірність виходу з ладу конденсатора дорівнює
11
3
. На-
вмання беруть 10 конденсаторів і вмикають паралельно в електрич-
ну мережу. Знайти найімовірніше число m
0
конденсаторів, які вий-
дуть із ладу, і обчислити відповідну ймовірність.
Відповідь.
3019897,0)2(;2
100
≈
= Pm .
12. Відомо, що серед виробів заводу стандартні деталі становлять
у середньому 85%. Скільки необхідно взяти цих деталей, щоб
m
0
= 65?
Відповідь.
76
00
=
+
≤≤
−
n
p
qm
n
n
pm
.
13. Імовірність того, що покупець, який завітав до взуттєвого ма-
газину, здійснить покупку, дорівнює в середньому 0,1. Яка ймовір-
ність того, що із 900 покупців, що завітали до магазину, здійснять
покупку: 1) 90 покупців; 2) від 100 до 180 покупців?
Відповідь. 1) 0,0443222, 2) 0,1335.
14. В яких межах має перебувати ймовірність появи випадкової
події в одному експерименті, коли відомо, що в
результаті проведен-
ня n = 600 незалежних експериментів за схемою Бернуллі m
0
= 60?
Відповідь.
601
61
601
60
1
1
1
00
≤≤→
+
+
≤≤
+
P
n
m
P
n
m
.
15. У партії однотипних деталей стандартні становить 82%. На-
вмання з партії беруть 400 деталей. Яка ймовірність того, що серед
них стандартних буде: 1) 355; 2) від 355 до 300. Знайти найімовір-
ніше число появи стандартних деталей m
0
і обчислити відповідну
ймовірність.
Відповідь.
052,0)328(;328;000071,0)2;0001041,0)1
4000
≈
=
≈
≈ Pm .
16. Імовірність виходу із ладу виробу під час його випробування
на надійність дорівнює 0,05. Яка ймовірність того, що під час ви-
пробувань 900 виробів із ладу вийдуть: 1) 30; 2) не більш як 30.
Відповідь. 1) 0,0044; 2) 0,0113.
17. Імовірність появи випадкової події в кожному з n незалежних
експериментів за схемою Бернуллі є величиною сталою і дорівнює
р = 0,8. Скільки
необхідно провести таких експериментів, щоб імо-
вірність появи випадкової події
900≥m дорівнювала 0,99?
Відповідь.
99,0
900
ФФ484416 =
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
→≈
npq
np
npq
npn
n
.
18. Телефонна станція обслуговує 1000 абонентів. Імовірність то-
го, що протягом години абонент розмовлятиме по телефону, дорівнює
