Жлуктенко В. І., Наконечний С. І. Теорія ймовірностей і математична статистика: У 2 ч. - Ч. І. Теорія ймовірностей
Подождите немного. Документ загружается.

108
Побудувати закон розподілу ймовірностей дискретної випа-
дкової величини Х — числа верстатів, які потребують уваги
робітника за певний проміжок часу. Знайти Мо.
Розв’язання.
Можливі значення випадкової величини:
Х = 0, 1, 2, 3.
Імовірності цих можливих значень такі:
p
1
= (0,2)
3
= 0,008;
p
2
= 3р q
2
= 3 ⋅ 0,8 ⋅ 0,04 = 0,096;
p
3
= 3p
2
q = 3 ⋅ 0,64 ⋅ 0,2 = 0,384;
p
4
= p
3
= (0,8)
3
= 0,512.
Запишемо закон таблицею:
х
і
0 1 2 3
р
і
0,008 0,096 0,384 0,512
Із таблиці визначаємо Мo = 3.
Отже, дістаємо одномодальний розподіл.
Приклад 6. За заданою щільністю ймовірностей
⎪
⎩
⎪
⎨
⎧
>
≤<−−+
−≤
=
.4,0
;42),4)(2(
;2,0
)(
x
xxxa
x
xf
Знайти а і F(x), Mo.
Розв’язання.
За умовою нормування маємо:
.
36
1
36481224)24(8)416(
3
864
8
3
82
)4)(2(
1
4
2
4
2
2
4
2
4
2
3
4
2
4
2
2
4
2
−=→−=−−=+−−−
+
=
=−−=−−→
−+
=
−
−
−
−
−−
−
∫∫∫
∫
a
xx
x
dxxdxdxx
dxxx
a
Щільність імовірностей зі знайденим а матиме вигляд
⎪
⎪
⎩
⎪
⎪
⎨
⎧
≥
<<−
+−
−≤
=
.4,0
;42,
36
)2)(4(
;2,0
)(
x
x
xx
x
xf
Графік f(x) зображено на рис. 53.
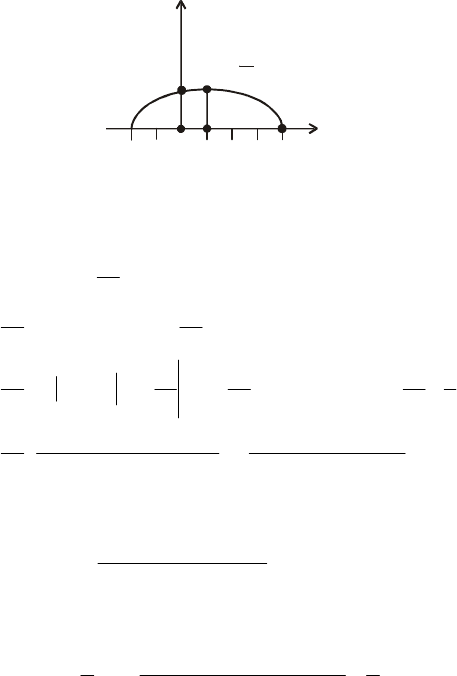
109
4
1
fx
()
–
2 0 1 4
x
А
(1, )
4
1
Рис. 53
Згідно з рис. 53 маємо f (1) = max. Отже, Мo = 1.
Визначаємо Мe:
.
108
32428
3
833624
36
1
3
8
3
4168
36
1
3
8
36
1
28
36
1
)28(
36
1
)2)(4(
36
1
)()(
3232
3
2
2
3
2
2
2
22 2
2
2
2
22
xxxxxx
x
xx
x
xx
dxxxdxdxdxxx
dxxxdxxfxF
x
x
x
xx xx
xx
−++
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−++
=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−−−++=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
−+=
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−+=−+=
=+−==
−
−
−
−− −−
−−
∫∫ ∫∫
∫∫
Отже,
⎪
⎪
⎩
⎪
⎪
⎨
⎧
>
≤<−
−++
−≤
=
.4,1
;42,
108
32428
;2,0
)(
32
x
x
xxx
x
xF
Для визначення Ме застосовуємо рівняння (83):
.1026243
2
1
108
32428
2
1
)(
23
32
=→=+−−→
→=
−++
→=
MeMeMeMe
MeMeMe
MeF
Ме можна знайти, скориставшись щільністю ймовірностей:
∫∫
∞−
∞
=
Me
Me
,)()( dxxfdxxf
(84)
або при Х ∈ [а; b]:
∫∫
=
Me
Me
)()(
a
e
dxxfdxxf
. (85)
Отже, Ме — можливе значення випадкової величини Х, причому та-
ке, що пряма, проведена перпендикулярно до відповідної точки на
площині Х = Ме, поділяє площу фігури, яка обмежена функцією f (x), на
дві рівні частини.

110
4. Дисперсія та середнє
квадратичне відхилення
Математичне сподівання не дає достатньо повної інформації про
випадкову величину, оскільки одному й тому самому значенню
М (Х) може відповідати безліч випадкових величин, які будуть різ-
нитися не лише можливими значеннями, а й характером розподілу і
самою природою можливих значень.
Приклад 7. Закони розподілу випадкових величин Х і Y за-
дані таблицями:
х
і
– 0,5 – 0,1 0,1 0,5
р
і
0,4 0,1 0,1 0,4
у
j
– 100 – 80 – 10 10 10 80
p
j
0,1 0,2 0,2 0,2 0,1 0,2
Обчислити М (Х) і М (Y).
Розв’язання.
.01016221610
1,01002,0802,0102,0102,0801,0100)(
;02,001,001,02,0
4,05,01,01,01,01,04,05,0)(
6
1
4
1
=+++−−−=
=⋅+⋅+⋅+⋅−⋅−⋅−==
=++−−=
=⋅+⋅+⋅−⋅−==
∑
∑
=
=
j
jj
s
іі
pyYМ
рxXM
Отже, два закони розподілу мають однакові математичні споді-
вання, хоча можливі значення для випадкових величин Х і Y істотно
різні. Із наведеного прикладу бачимо, що в разі рівності математич-
них сподівань (М (X) = М (Y) = 0) випадкові величини Х і Y мають
тенденцію до коливань відносно М (X) та М (Y),
причому Y має бі-
льший розмах розсіювання відносно М (Y), ніж випадкова величина
Х відносно М (Х). Тому математичне сподівання називають центром
розсіювання. Для вимірювання розсіювання вводиться числова ха-
рактеристика, яку називають дисперсією.
Для визначення дисперсії розглядається відхилення випадкової
величини Х від свого математичного сподівання (Х – М (Х))
Математичне сподівання такого
відхилення випадкової величини
Х завжди дорівнює нулю. Справді,
0)()())(()())((
=
−
=
−
=
− XMXMXMMXMXMXM
.
111
Отже, відхилення не може бути мірою розсіювання випадкової
величини.
Дисперсією випадкової величини Х називається математичне
сподівання квадрата відхилення цієї величини
2
))(()( XMXMXD −=
. (86)
Для дискретної випадкової величини Х дисперсія
і
n
і
і
рХМхXD
2
1
))(()( −=
∑
=
; (87)
для неперервної
dxxfXMxXD )())(()(
2
∫
∞
∞−
−=
. (88)
Якщо Х
∈
[а; b],
то
dxxfХМхXD
ъ
а
)())(()(
2
∫
−=
. (89)
5. Властивості дисперсії
1. Якщо С — стала величина, то
0)(
=
CD
. (90)
Справді
0)0()())(()(
22
==−=−= MCCMCMCMCD
.
2.
)()(
2
XDCCXD =
. (91)
Маємо:
)())((
))((())(())(()(
222
222
XDCXMXMC
XMXCMXCMCXMCXMCXMCXD
=−=
=−=−=−=
3. Якщо А і В — сталі величини, то
(
)
XDABAXD
2
)( =+ . (92)
Адже
).())(())((
))(())(()(
2222
22
XDAXMXMAXAMAXM
BXAMBAXMBAXMBAXMBAXD
=−=−=
=−−+=+−+=+
Дисперсію можна обчислити і за такою формулою:
).()()(
22
XMXMXD −= (93)

112
Доведення. Згідно з (86) дістаємо:
).()()()(2)(
))(()()(2)(
))()(2())(()(
22222
22
222
XMXMXMXMXM
XMMXMXMXM
XMXXMXMXMXMXD
−=+−=
=+−=
=+−=−=
Для дискретної випадкової величини Х
)()(
2
1
2
ХМрхXD
n
і
іі
−=
∑
=
; (94)
для неперервної
∫
∞
∞−
−= )()()(
22
XMdxxfxXD . (95)
Якщо Х
∈
[а; b], то
).()()(
22
XMdxxfхXD
b
а
−=
∫
Слід пам’ятати, що дисперсія не може бути від’ємною величи-
ною
(
)()
0≥XD .
Отже, дисперсія характеризує розсіювання випадкової величини
відносно свого математичного сподівання. Якщо випадкова величи-
на виміряна в деяких одиницях, то дисперсія вимірюватиметься в
цих самих одиницях, але в квадраті.
Тому доцільно мати числову характеристику такої самої вимір-
ності, як і випадкова величина. Такою числовою характеристикою є
середнє квадратичне відхилення.
Середнім квадратичним
відхиленням випадкової величини Х на-
зивають корінь квадратний із дисперсії:
(
)
)(XDX =σ
. (97)
Приклад 8. Закон розподілу дискретної випадкової величи-
ни Х задано таблицею:
х
і
– 4 – 2 1 2 4 6
р
і
0,1 0,2 0,3 0,2 0,1 0,1
Обчислити D (X), σ (X).
Розв’язання. Згідно з (94) маємо:
;)()()(
2
6
1
6
1
222
⎟
⎠
⎞
⎜
⎝
⎛
−=−=
∑∑
== і
іі
і
і
і
рхрхXMXMXD
!
113
;9,06,04,04,03,04,04,0
1,061,042,023,012,021,04)(
6
1
=++++−−=
=⋅+⋅+⋅+⋅+⋅−⋅−==
∑
=і
іі
рхХМ
()
.8,289,7)(
;89,781,07,8)9,0(7,8)(
;7,86,36,18,03,08,06,1
1,0361,0162,043,012,041,016)(
2
6
1
2
2
≈==σ
=−=−=
=+++++=
=⋅+⋅+⋅+⋅+⋅+⋅==
∑
=
XDX
XD
рхXM
і
іі
Приклад 9. Маємо чотири електролампочки, кожна з яких
має дефект з імовірністю q = 0,1 (p = 1 – q = 0,9 — імовір-
ність того, що в лампочці дефект відсутній). Послідовно бе-
руть по одній лампочці, вгвинчують у патрон і вмикають
електричний струм. Під час вмикання струму лампочка з
дефектом перегорить, і її замінять на іншу. Побудувати за
-
кон розподілу дискретної випадкової величини Х — число
лампочок, які будуть випробувані. Обчислити σ (X).
Розв’язання. Дискретна випадкова величина Х — число лампочок,
які будуть випробувані — набуває таких можливих значень:
.4;3;2;1
4321
=
=
=
=
хххx
Обчислимо відповідні ймовірності:
.001,00001,00009,0)4(
;009,0)3(;09,0)2(;9,0)1(
43
4
2
321
=+=+===
===========
qpqpXP
pqpXPpqpXPpXP
Адже четверта лампочка буде випробувана, коли третя перегорить, а
четверта — ні, або коли й четверта перегорить.
У табличній формі закон розподілу Х матиме такий вигляд:
х
і
1 2 3 4
р
і
0,9 0,09 0,009 0,001
Далі виконуємо такі обчислення:
;111,1004,0027,018,09,0
001,04009,0309,029,01)(
4
1
=+++=
=⋅+⋅+⋅+⋅==
∑
=
і
і
і
рхXM
;357,1016,0081,036,09,0
001,016009,0909,049,01)(
4
1
2
2
=+++=
=⋅+⋅+⋅+⋅==
∑
=
і
і
і
рхХМ
114
.35,0122679,0)()(
;122679,0234321,1357,1)111,1(357,1)()()(
2
2
2
≈==σ
=−=−=−=
XDX
XMXMXD
Приклад 10. Закон розподілу ймовірностей дискретної ви-
падкової величини Х задано функцією
⎪
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎪
⎨
⎧
>
≤<
≤<
≤<
≤<−
−≤<−
−≤
=
.8,1
;85,8,0
;53,6,0
;31,4,0
;14,3,0
;46,1,0
;6,0
)(
x
x
x
x
x
x
x
xF
Обчислити D (X); σ (X).
Розв’язання. За заданою функцією розподілу ймовірностей подамо
закон розподілу таблицею
х
і
– 6 – 4 1 3 5 8
р
і
0,1 0,2 0,1 0,2 0,2 0,2
.78,489,22)()(
;89,2261,35,26)9,1(5,26)()()(
;25,268,1258,11,02,36,3
2,0642,0252,091,012,0161,036)(
;9,16,116,01,08,06,0
2,082,052,031,012,041,06)(
222
6
1
2
2
6
1
≈==σ
=−=−=−=
=+++++=
=⋅+⋅+⋅+⋅+⋅+⋅==
=++++−−=
=⋅+⋅+⋅+⋅+⋅−⋅−==
∑
∑
=
=
XDX
XMXMXD
рхХМ
рхXM
і
і
і
і
іі
Приклад 11. Задано щільність імовірностей:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
π>
π≤<
≤
=
.,0
;0,sin
2
1
;0,0
)(
x
xx
x
xf
Обчислити D (X); σ (X). Знайти Мо; Ме.
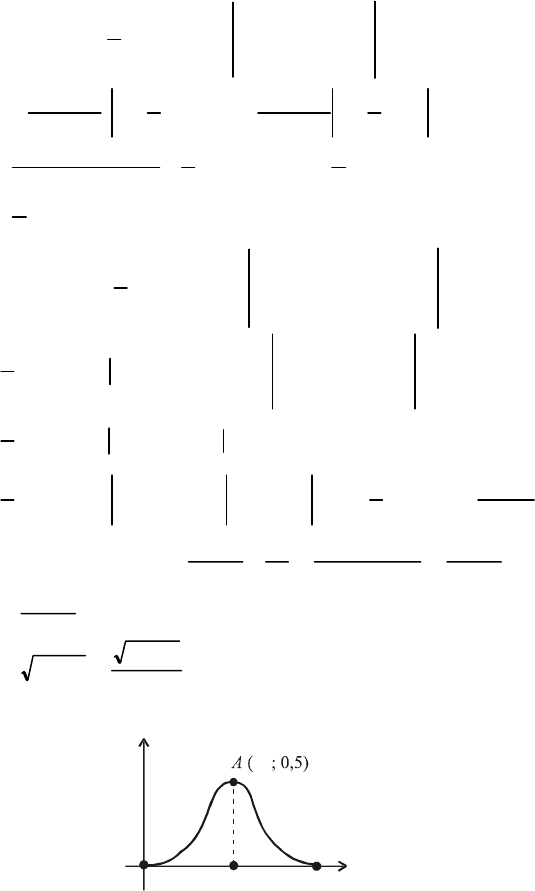
115
Розв’язання.
;
2
)(
;
2
)0sin(sin
2
1
2
0cos0cos
sin
2
1
2
cos
cos
2
1
2
cos
cos
sin
,
sin
2
1
)()(
00
0
0
00
π
=
π
=−π+
+ππ−
=
=+
−
=+
−
−=
=
−=→
→=
==
===
ππ
π
π
ππ
∫
∫∫
XM
x
xx
xdx
xx
xv
dvdx
dxduxu
xdxxdxxxfXM
;
2
2
)2(
2
1
cossin2cos
2
1
sinsin2cos
2
1
sin
cos
,
cos2cos
2
1
cos
sin
2,
sin
2
1
)()(
2
2
000
2
0
0
0
2
0
0
2
2
0
2
0
22
−π
=−π=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
++−=
=
⎥
⎦
⎤
⎢
⎣
⎡
⎟
⎠
⎞
⎜
⎝
⎛
−+−=
=
=
=
==
=
⎟
⎠
⎞
⎜
⎝
⎛
+−=
=
−=→
→=
==
===
πππ
π
π
π
π
π
ππ
∫
∫
∫∫
xxxxx
xdxxxxx
xv
dvdx
dxduxu
xdxxxx
xv
dvxdx
xdxduxu
dxxxdxxfxXM
.
2
4
)()(
;
4
4
)(
;
4
4
4
42
42
2
)()()(
2
2
22222
22
−π
==σ
−π
=
−π
=
π−−π
=
π
−
−π
=−=
XDX
XD
XMXMXD
Графік f (x) зображено на рис. 54.
2
π
2
π
f
x
()
0
x
π
2
π
2
π
–
–
Рис. 54
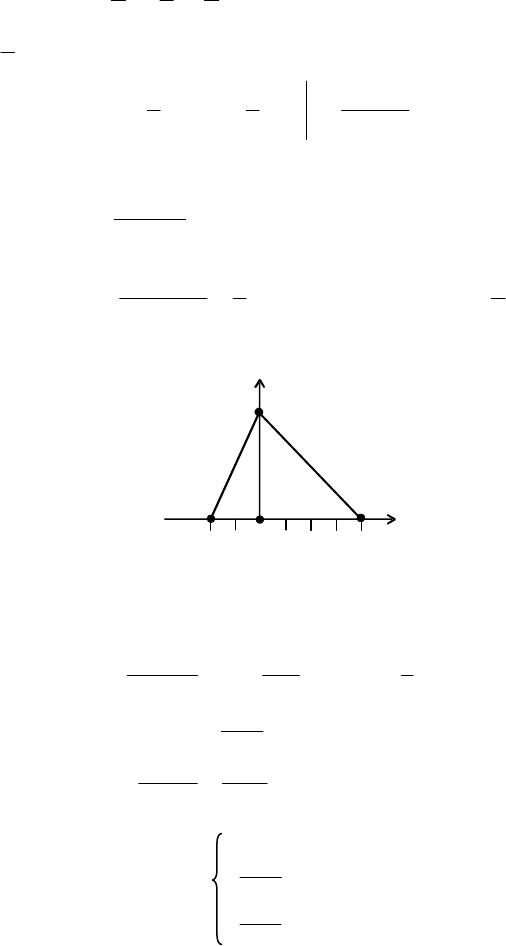
116
Оскільки 5,0
2
sin
2
1
2
=
π
=
⎟
⎠
⎞
⎜
⎝
⎛
π
f
є максимальним значенням, то
.
2
Mo
π
=
Знаходимо F(x) =
.
2
cos1
cos
2
1
sin
2
1
0
0
x
xdx
х
x
−
=−=
∫
Отже,
2
0
2
1
2
1
)(
.,1
;0,
2
cos1
;0,0
)(
π
=→=→=
−
=
⎪
⎪
⎩
⎪
⎪
⎨
⎧
π>
π≥<
−
≤
=
МеMесоs
Mе
MеF
x
x
x
x
xF
сos
Приклад 12. Задано щільність імовірностей (рис 55).
3
1
f
x
()
–
2 0 2 4
x
А
C
(–2; 0)
B
(0; )
3
1
–
Рис. 55
Обчислити D (X); σ (X); Mе. Знайти Мо.
Розв’язання. За умовою нормування знайти ординату точки В:
3
1
1
2
76
1
2
=→=
⋅
→=
⋅
y
OBAB
.
На проміжку [–2; 0]
()
6
2+
=
x
xf
.
На [0; 4]
()
12
4
12
)4( xx
xf
−
=
−
−=
.
Отже, щільність імовірностей
=
)(xf
.4,0,
12
4
;02,
6
2
;2,0
>
−
≤<−
+
−≤
x
x
x
x
x
117
Знаходимо функцію розподілу ймовірностей:
На проміжку [–2; 0]
.
12
)2(
6
2
)(
2
2
+
=
+
=
∫
−
xx
xF
x
На [–2; 4]
=
−
−=
−
+=
∫
0
2
0
24
)4(
12
4
12
4
)0()(
х
x
x
dx
x
FxF
=
24
16
24
)4(
12
4
2
+
−
−
x
.
24
)4(
1
24
)4(
3
2
3
1
22
−
−=
−
−+=
xx
Отже, функцію розподілу ймовірностей можна подати у вигляді
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
>
≤<
−
−
≤<−
+
−≤
=
.4,1
;40,
24
)4(
1
;02,
12
)2(
;2,0
)(
2
2
x
x
x
x
x
x
xF
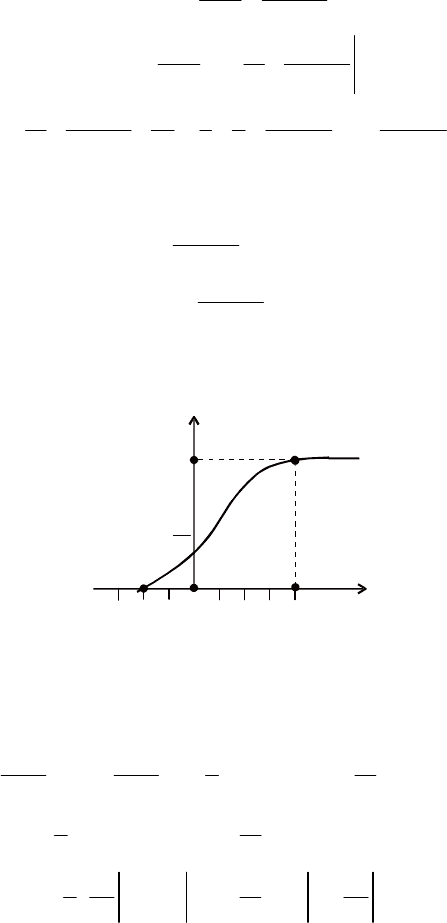
Графік F(x) зображено на рис. 56.
3
1
Fx
()
–
2 0 4
x
1
3
1
Рис. 56
Далі обчислюємо D (X):
∫∫
−
=+=
0
2
4
0
)()()( dxxxfdxxxfXM
∫∫∫∫
=−++=
−
+
+
=
−−
4
0
2
0
2
2
4
0
0
2
)4(
12
1
)2(
6
1
12
4
6
2
dxxxdxxxdx
x
xdx
x
x
=
⎟
⎠
⎞
⎜
⎝
⎛
−+
⎟
⎠
⎞
⎜
⎝
⎛
+=
∫∫∫∫
−−
4
0
4
0
2
0
2
0
2
2
4
12
1
2
6
1
dxxхdxxdxdxx
=
⎟
⎠
⎞
⎜
⎝
⎛
−+
⎟
⎠
⎞
⎜
⎝
⎛
+=
−− 0
4
3
0
4
2
2
0
2
2
0
3
3
2
12
1
36
1 x
xx
x
