Zdunkowski W., Trautmann T., Bott A. Radiation in the atmosphere: A course in Theoretical Meteorology

Подождите немного. Документ загружается.

11.4 Perturbation theory and ozone proﬁle retrieval 435

Next we have to consider the adjoint radiance ﬁeld I

, which is given by the

solution of the adjoint radiative transfer equation

(z, Ω) = Q

(z, Ω) (11.103)

where Q

is the source of adjoint photons, and the adjoint operator L

is deﬁned

=−µ

∂

∂z

ext

(z) −

sca

(z)

4π



4π



P(z, Ω



→ Ω) −

δ(z)U(−µ)|µ|U (µ



)|µ





◦ d



(11.104)

Note that in (11.104) as compared to (11.98) the direction µ is inverted. Similarly

to this reversion of the zenith angle the meaning of the boundary conditions for the

adjoint radiance ﬁeld has to be changed from the incoming forward radiation ﬁeld

to the outgoing radiance, cf. (5.23)

top of the atmosphere: I

,µ,ϕ) = 0, 0 ≤ ϕ ≤ 2π,0<µ≤ 1

Earth’s surface: I

(0,µ,ϕ) = 0, 0 ≤ ϕ ≤ 2π, −1 ≤ µ<0

(11.105)

We repeat from Chapter 5 the meaning of the pseudo-radiance

(z, Ω) = I

(z, −Ω) (11.106)

by pointing out that (z,µ,ϕ) is the solution to the usual forward radiative transfer

equation possessing a particular source

L(z, Ω) = Q

(z, −Ω) (11.107)

Again it is noteworthy that for the pseudo-radiance ﬁeld  the direction of the

propagating adjoint photons has to be inverted in the adjoint source Q

with respect

to the upper and lower 2π hemisphere. Therefore, the transformation (11.106)

allows us to use the same standard method of ﬁnding the solution for the adjoint

radiance ﬁeld as it is applied for the forward radiance ﬁeld I (z,µ,ϕ).

Next we wish to illustrate how the ﬁrst derivative of the reﬂectance with respect

to the state vector x is related to the perturbation integral. Let us suppose that we

have found the solutions I

and I

for an atmospheric base state (subscript 0)

characterized by the state vector x

. Following the procedure outlined in Chapter 5

and resulting in (5.66), the reﬂectance for a perturbed atmosphere to ﬁrst-order

accuracy may be approximated by the linear expansion

r(x) ≈ r(x

) −



k=1

I

,L

 (11.108)

436 Remote sensing applications of radiative transfer

Here L

is the change of the differential operator L if we only perturb the k-th

component of the state vector x

by x

. By comparing this equation with (11.96)

we ﬁnd for the ﬁrst derivative of the reﬂectance r with respect to the physical

parameters x

∂r

∂x

=−

x

I

,L



(11.109)

Our particular interest lies in perturbing either the ozone molecule concentration

in units of molecules per m

of air in the k-th homogeneous atmospheric

sublayer or the Lambertian albedo A

of the ground. For this we derive the ﬁrst

derivatives of the reﬂectance with respect to the ozone proﬁle and the surface albedo.

If ρ

is the mean ozone molecule concentration in the sublayer k and ρ

,k,0

the corresponding unperturbed value, then the perturbation x

is given by

x

= ρ

= ρ

− ρ

,k,0

(11.110)

Because we only perturb ρ

, the change in the absorption optical depth τ

of sublayer k may be written as

τ



k−1

(ρ

− ρ

,k,0

)σ

dz =−σ

ρ

− z

k−1

) (11.111)

where σ

is the absorption cross-section of an ozone molecule and (z

, z

k−1

) refer

to the lower and upper boundary of the k-th homogeneous sublayer of the model

atmosphere. Furthermore, we easily see that, for this particular perturbation, L

in the perturbation integral (11.108) is

L



ρ

, z

< z < z

k−1

0, else

(11.112)

Therefore, we directly ﬁnd the ﬁrst derivative of r with respect to the mean ozone

molecule concentration in sublayer k

∂r

∂ρ

=−

ρ

I

,L

=−σ



k−1



4π



(z, −Ω)I

(z, Ω)ddz

(11.113)

where we have replaced I

by means of (11.106).

For the perturbation of the surface albedo, A

= A

− A

g,0

, where A

g,0

is the

Lambertian albedo for the unperturbed ground, we similarly ﬁnd from (11.98)

L =−



4π

A

δ(z)U(µ)|µ|U (−µ



)|µ



|◦d



(11.114)

11.4 Perturbation theory and ozone proﬁle retrieval 437

Due to the appearance of the delta function δ(z), the integration over z simpli-

ﬁes to the evaluation of the radiances 

and I

at ground level z = 0. Thus the

corresponding ﬁrst derivative of r with respect to the surface albedo A

is given by

∂r

∂ A

=−

A

I

,LI

=

−

(

−

)

(11.115)

Here the quantities E

−

(

) and E

−

) represent downward ﬂux densities at ground

level of the base atmosphere’s pseudo-radiance ﬁeld 

(0,) and the forward

radiance ﬁeld I

(0,), respectively, i.e.

−

(

) =



4π

U (−µ)|µ|

(0, Ω)d

−

) =



4π

U (−µ)|µ|I

(0, Ω)d

(11.116)

Note that in these expressions the Heaviside step function U (−µ) just selects all

radiation coming from the upper 2π hemisphere.

Substituting (11.113) and (11.115) into (11.96) yields the reﬂectance r (x) of the

actual atmosphere as function of the reﬂectance r(x

) of a given base atmosphere.

Landgraf et al. (2001) applied the forward–adjoint perturbation theory to calcu-

late the derivatives of the reﬂectance with respect to the ozone concentration and

the surface albedo. They also compared the results with benchmark calculations

which have been performed with the DISORT programme package as provided

by Stamnes et al., (1988), see also Section 4. Since in the DISORT calculations

expressions for the partial derivatives of r with respect to ρ

and A

, such as

(11.113) and (11.115), are not available, the following discretizations are used in

these benchmark calculations

∂r

∂ρ

≈

r(ρ

+ ρ

) − r (ρ

)

ρ

∂r

∂ A

≈

r(A

+  A

) − r (A

)

A

(11.117)

Figure 11.12a shows the derivatives of r with respect to the ozone concentration.

In the left panel of the ﬁgure the vertical proﬁle of ∂r/∂ρ

has been computed on

the basis of the perturbation theory. These computations have been carried out for

the three wavelengths of 299 (solid), 312 (dotted), and 323 nm (dashed). The ﬁgure

has to be interpreted as follows: in regions where the curves attain large values, the

sensitivity of the reﬂected radiation with respect to a unit ozone perturbation in the

associated altitude range is signiﬁcant. This is the case for all altitudes above 12 km.

A negative value for ∂r/∂ρ

means that r decreases if the molecule concentration

of ozone is increased in the particular model layer. For similar perturbations of the

ozone proﬁle in the middle and lower troposphere this sensitivity decreases with

438 Remote sensing applications of radiative transfer

299 nm

312 nm

323 nm

−4 −3 −2 −1 −4 −20024

∂r/∂p (10

−16

)

δ (10

−2

% )

z (km)

Fig. 11.12 Derivatives ∂r/∂ρ (ρ = ρ

) as computed with the forward-adjoint

linear perturbation theory. Results are shown for three selected wavelengths λ =

299, 312, 323 nm. The right part of the ﬁgure shows the relative difference δ

between the linear perturbation theory and ﬁnite difference results obtained with

DISORT. After Landgraf et al. (2001).

decreasing altitude. For the shorter UV wavelengths the clear-sky atmosphere is

optically so thick that photons scattered in the lower part of the atmosphere do not

make any signiﬁcant contribution to the backscattered light observed by the satellite

instrument. Hence, we conclude that it is rather difﬁcult to retrieve the ozone proﬁle

in the troposphere with satisfactory accuracy.

The right panel of Figure 11.12 depicts the relative difference δ (in 10

−2

between the forward–adjoint approach (11.113) and the ﬁnite difference approach

(11.117) based on DISORT calculations. Again the computations have been per-

formed for clear sky conditions involving only Rayleigh scattering and ozone

absorption. The results shown apply to a solar zenith angle of ϑ

= 45

◦

and a view-

ing zenith angle of ϑ

= 10

◦

. It can be seen that the linear perturbation approach

nearly perfectly reproduces the partial derivatives with relative errors smaller than

about 0.03%.

The upper part of Figure 11.13 shows the sensitivity of the reﬂectance with

respect to the surface albedo. The solid curve denotes results with a clear sky

11.4 Perturbation theory and ozone proﬁle retrieval 439

λ (nm)

1.5

1.0

0.5

0.0

−5

−10

300 310 320 330

δ (10

−2

∂r /∂A (1)

Fig. 11.13 Derivatives ∂r/∂ A

(upper part with A = A

) and relative differ-

ences between the linear perturbation results and the DISORT approach employ-

ing ﬁnite differencing (lower part). The parameters for these computations were

= 45

◦

, ϑ

= 10

◦

, and A

= 0.1. Solid curves: atmosphere without aerosol

particles, dotted curves: atmosphere containing aerosol particles. After Landgraf

et al. (2001).

atmosphere containing no aerosol particles while for the dotted line a typical rural

aerosol scenario has been adopted. The optical parameters of the aerosol particles

were taken from Shettle and Fenn (1979). For the wavelength of 330 nm the total

aerosol optical depth attained a value of 0.85.

As can be seen from the ﬁgure, for the smaller wavelengths ∂r/∂ A

converges

to zero. This can be explained by the fact that solar photons do not reach the

surface because they are already absorbed by the stratospheric ozone. This result

has an important consequence: Any ozone data retrieved with a particular inversion

method will turn out to be insensitive to a possibly unknown value of the Lambertian

surface albedo. Thus, regarding the surface properties it would make no difference

if the retrieval is made over the ocean or over a surface covered by snow or ice.

Figure 11.13 also shows that for increasing wavelength ∂r/∂ A

increases with λ.

For larger values of λ the wavelength dependence of the sensitivity decreases again.

The lower part of Figure 11.13, depicting the difference between the perturbation

theory and the DISORT approach, reveals that the derivatives of r with respect to

can be accurately computed with the linear radiative perturbation theory. The

relative errors are always smaller than about 0.05%.

440 Remote sensing applications of radiative transfer

11.5 Appendix

11.5.1 Example for an ill-posed inversion problem

In Section 11.3.1 we have pointed out that due to the quasi-singular matrix A the

solution to (11.61) may become unstable. Now we will illustrate this feature by

virtue of a simple example. Experience with inversion methods tells us that small

perturbations in the observations g may lead to extreme perturbations in the physical

solution f. This is the typical situation in case of ill-posedness. Let us brieﬂy discuss

the deﬁnition of a well-posed mathematical problem, see Hansen (1994).

(1) For each g there exists a solution f for which Af = g.

(2) The solution f is unique.

(3) Small perturbations in g cause only small perturbations for the solution f.

If, for a particular problem, one of these conditions is not fulﬁlled, the problem

is said to be ill-posed. Let us illustrate this with a simple example as discussed by

Craig and Brown (1986). As weighting function or kernel K(x, y) of the integral

equation we use the Heaviside step function

U (y) =



0, y ≤ 0

1, y > 0

(11.118)

The problem to be solved is the Volterra integral equation of the ﬁrst kind for f (y)

g(x) =



f (y)dy =



U (x − y) f (y)dy, x ∈ [a, b] (11.119)

The solution to the inversion problem for (11.119) is simply the ﬁrst derivative of

the function g

f (y) =



x=y

(11.120)

This can be easily veriﬁed by inserting (11.120) into (11.119).

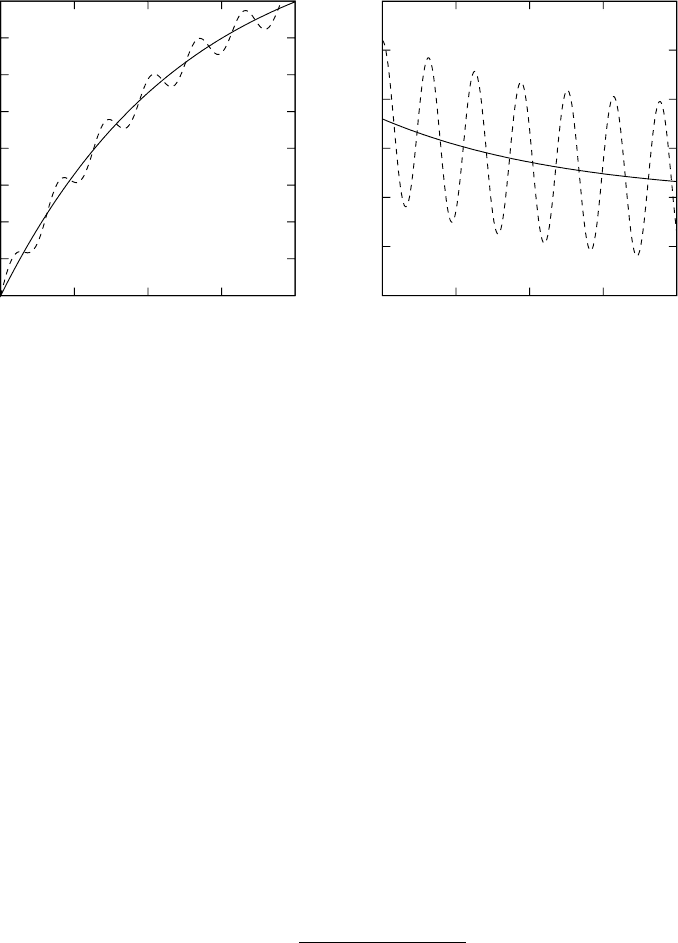
Figure 11.14 depicts the solutions f

and f

which correspond to the two

‘measurements’

(x) = 1 − exp

(

−αx

)

(x) = g

(x) +β sin(ωx)

(11.121)

with α = 0.8, β = 0.04 and ω = 20. Note that the term sin(ωx) can be understood

as a small perturbation of the measurement g

having an amplitude β. From (11.120)

we ﬁnd for the solutions of the inversion problem

(y) = α exp

(

−αy

)

(y) = f

(y) +ωβ cos(ωy)

(11.122)

11.6 Problems 441

−1

0 0.5 1 1.5 2 0 0.5 1 1.5 2

−0.5

0.5

1.5

0.8

0.7

0.6

0.5

0.4

0.3

0.2

0.1

Fig. 11.14 Example for an ill-posed inversion problem. The left panel shows the

measurements (solid curve: exact measurement g

, dashed curve: measurement

with perturbations g

). The right panel depicts the corresponding inversions f

and f

It is clear that the perturbations in g

due to the sine term are in the range of a few

percent with respect to the measured unperturbed signal g

. Nevertheless, for y > 1

the perturbations in the solution f

can amount to several 100% of the true solution

, see Figure 11.12. Therefore, the solution of the inversion problem (11.119)

becomes already unstable for small changes in the observation g.

The typical situation in inverse remote sensing problems is that, unlike to the

simple case above, it is not possible to ﬁnd full analytical solutions of the Fredholm

integral equation by virtue of complete function systems (e.g. orthogonal polyno-

mials). Therefore, one formulates the inverse problem in its discretized form and

searches for a solution employing methods of linear algebra.

11.6 Problems

11.1: Show that in the Bouguer–Langley method the slope of the regression line

is given by

ln(E

λ,2

) − ln(E

λ,1

)

− m

11.2: Suppose that the absorption coefﬁcient decreases with height according

to k(z) = k(z = 0) exp(−z/H) where H is a positive constant. Find the

height where the weighting function has its maximum. Assume that the

transmission function follows an exponential law.

442 Remote sensing applications of radiative transfer

11.3: By carrying out the matrix multiplications, show that (11.70) is equivalent

to (11.67).

11.4: Verify (11.80).

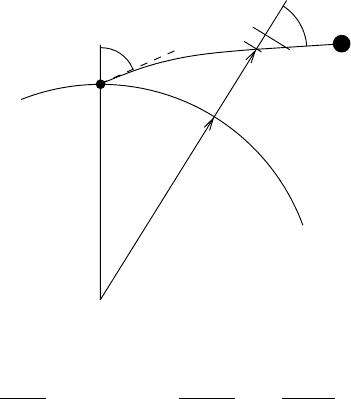
11.5: Formula (11.7) is purely empirical. A suitable air mass formula for dry air

scattering can be derived with the help of the ﬁgure below, the deﬁnition

m = (



∞

ρds)/(



∞

ρdz) and the basic astronomic formula (1 + δ)(R +

z) sin ζ = con s t, see the ﬁgure.

Sun

Observer

Show that

m =



∞



1 −



1 + δ





R + z



sin

−1/2

with H

= p

/(gρ

) and N = 1 + δ is the index of refraction of the air.

The sufﬁx 0 refers to the ground. Usually one assumes that δ/δ

= ρ/ρ

Inﬂuence of clouds on the climate of the Earth

In the ﬁnal chapter of this book we will brieﬂy treat the radiative inﬂuence of

clouds on the climate of the Earth. A brief introduction to this topic has already

been presented in the ﬁrst chapter where we have discussed the radiation budget of

the Earth. In the chapters that followed we have studied the radiative transfer theory

in some detail and have learned how to calculate the radiances and ﬂux densities in

the solar and long-wave spectrum.

We have omitted any discussion of measurement programs such as the satellite

experiments ERB and ERBE which were speciﬁcally devised to study the global

radiation budget. A brief description of some of the sophisticated instrumentation

used to measure the reﬂected solar energy and the outgoing long-wave radiation is

given by Lenoble (1993) where many references to this topic can be found.

Globally the planet Earth is in radiative equilibrium implying that the reﬂected

solar radiation and the outgoing long-wave radiation are in balance with the incom-

ing solar radiation. If this balance is disturbed by natural or by anthropogenic pro-

cesses the global climate will be changed. A detailed study of the radiative impact

of clouds on the climate is very difﬁcult and can be carried out only with the help

of sophisticated climate models. The reason for this is that many different variables

that are responsible for the evolution of the climate interact in a highly nonlinear

way. Here we will give a very simple discussion only following the arguments

presented by Arking (1991).

12.1 Cloud forcing

The outgoing long-wave radiation E

l,t

at the top of the atmosphere can be calculated

with the help of one of the radiative transfer methods which we have previously

discussed. Accepting the insufﬁciency of any empirical formula, we use the Budyko

443

444 Inﬂuence of clouds on the climate of the Earth

expression

l,t

= 223.0 + 2.2T

− (48.0 + 1.6T

)C (12.1)

to calculate E

l,t

where T

is the air temperature near the ground and C the cloud

fraction ranging from 0 to 1. In order to obtain E

l,t

in units of (W m

−2

), the tem-

perature T

must be expressed in degrees Celsius. The variation of E

l,t

with cloud

fraction C results in the so-called sensitivity coefﬁcient for long-wave radiation δ

as deﬁned by

∂ E

l,t

∂C

=−(48.0 + 1.6T

) (12.2)

For a constant mean global surface temperature T

= 15

◦

C, δ

assumes the value

of −72 W m

−2

Analogously, the sensitivity coefﬁcient for solar radiation δ

can be deﬁned by

considering the solar ﬂux density E

s,t

at the top of the atmosphere. If A

stands

for the average albedo of the overcast sky, A

for the albedo of the cloud-free

atmosphere then E

s,t

is expressed by

s,t

(1 − A) =

[

1 − A

C − A

(1 − C)

]

(12.3)

where A = A

C + A

(1 − C) is a weighted average global albedo with the cloud

fraction as weighting factor. In analogy to (12.2) the sensitivity coefﬁcient for solar

radiation δ

is deﬁned by

∂ E

s,t

∂C

=−

− A

) (12.4)

Assuming S

=1368 W m

−2

, A

= 0.5 and A

= 0.12 which appear to be reason-

able values, the sensitivity coefﬁcient is δ

=−130Wm

−2

Let us now brieﬂy discuss the effect of clouds on the radiation budget at the top

of the atmosphere. As follows from (12.3) and simple reasoning, an increase in

cloud fraction C increases the reﬂectance at the top of the atmosphere level thus

reducing the energy gain for the system Earth–atmosphere. However, an increase

in cloud fraction also reduces the outgoing long-wave radiation at the top of the

atmosphere because clouds are colder than the Earth’s surface. This fact is also

stated by the minus sign of the last term of (12.1).

We will now introduce the net sensitivity coefﬁcient which is the difference

between the solar and long-wave radiation sensitivity coefﬁcients as expressed by

δ = δ

− δ

∂ E

s,t

∂C

−

∂ E

l,t

∂C

=−

− A

)



1 −

∂ E

l,t

∂C

∂ E

s,t

∂C



(12.5)

Thus, δ amounts to −58 W m

−2

. Certainly, this number is no more than a crude

estimate, but it gives us an impression of the order of magnitudes which are involved.