Зайцевский А.В. Релятивистская теория электронного строения молекул
Подождите немного. Документ загружается.


Ω
Ω
†
= Ω
−1
Ω
†
HΩ = P
L
Ω
†
HΩP
L
+ P
R
Ω
†
HΩP
R
= (Ω
†
HΩ)
LL
+ (Ω
†
HΩ)
RR
,
(Ω
†
HΩ)
LR
= 0 (Ω
†
HΩ)
RL
= 0,
Ω
H
eff
= P
L
Ω
†
HΩP
L
E
H
RR
−c
2
H
eff
(E)
E
E
{0}
H
eff
(E
{0}
)
E
{1}
H
eff
(E
{1}
)
ψ
L
= ψ
L
, ψ
R
= ψ
S
,
H
LL
= V, H
LR
= c(σ, p), H
RR
= V −2c
2
H
eff
(E) = V + c
2
(σ, p)(E − V + 2c
2
)
−1
(σ, p)
= V +
1
2
(σ, p)
1 −
V − E
2c
2
!
−1
(σ, p)

ψ
R
ψ
S
ψ
L
ψ
R
Ψ
†
Ψ = ψ
†
L
ψ
L
+ ψ
†
R
ψ
R
,
ψ
†
L
ψ
L
ψ
R
= ψ
S
= (2c
2
− V + E)
−1
(σ, p)ψ
L
Ψ
†
Ψ = ρ = ψ
†
L
(1 + N) ψ
L
,
N = c
2
(σ, p)(2c
2
+ E − V )
−2
(σ, p).
ψ
L
→ ψ
′′
L
= Uψ
L
, U = (1 + N)
1/2
,
H
′′
eff
= (1 + N)
1/2
H
eff
(1 + N)
−1/2
.
ρ = ψ
′′ †
L
ψ
′′
L
V
V
V
H
eff

H
eff
H
eff
H
RA
eff
= V +
1
2
(σ, p)
1 −
V
2c
2
!
−1
(σ, p).
c
−2
b
S ≈
1 0
0 0
,
V ψ
L
+
p
2
2
ψ
b
L
= Eψ
L
p
2
2
ψ
L
−
p
2
2
−
(σ, p)V (σ, p)
4c
2
ψ
b
L
= 0.
V +
p
2
2
p
2
2
−
(σ, p)V (σ, p)
4c
2
−1
p
2
2
= V +
1
2
p
2
(σ, p)
1 −
V
2c
2
!
(σ, p)
!
−1
p
2
= V +
1
2
(σ, p)
1 −
V
2c
2
!
−1
(σ, p).

1/c
c
−2
1 −
V − E
2c
2
!
−1
≈ 1 +
V − E
2c
2
≈ 1 +
V − E
0
2c
2
,
E
0
1 + N ≈ 1 +
p
2
4c
2
, U = (1 + N)
1/2
≈ 1 +
p
2
8c
2
, U
−1
≈ 1 −
p
2
8c
2
,
H
′′
eff
≈
1 +
p
2
8c
2
V +
p
2
2
+
(σ, p)V (σ, p) − E
0
p
2
4c
2
1 −
p
2
8c
2
.
c
−4
H
′′
eff
≈ V +
p
2
2
+
1
4c
2
(σ, p)V (σ, p) − E
0
p
2
+
p
2
V − V p
2
2
.
(σ, p)V (σ, p) H
′′
eff
H
′′
eff
≈ V +
p
2
2
+
1
4c
2
1
2
(∆V ) + p
2
(V − E
0
) + (σ, (∇V ) × p)
!
.

E
0
−V
p
2
(V − E
0
) −→ −p
4
/2.
H
′′
eff
= V +
p
2
2
+
1
c
2
(G
MV
+ G
D
+ G
SO
)
G
MV
= −
p
4
8
, G
D
=
(∆V )
8
,
G
SO
=
1
4
(σ, (∇V ) × p) ,
G
SO
G
MV
G
D
E
MV
E
D
E
SO
Q
1/c
2

1s e
−ζr
E
var
(ζ) =
ζ
2
2
− Qζ −
5ζ
4
8c
2
+
Qζ
3
4c
2
ζ
1/c
1 −
V − E
2c
2
!
−1
1/c
|V −E| ≪ 2c
2
|V − E| ≥ 2c
2
1/c
Ω = Ω
0
Ω
1
.
Ω
0
Ω
1
Ω
†
1
=
1 + X
2
1
1/2
+ X
1
,
X
1
X
†
1
= −X
1

Ω
1
X
1
Ω
†
H
D
Ω
X
1
X
1
(Ω
†
H
D
Ω)
LS
(Ω
†
H
D
Ω)
LL
Ω
†
H
D
Ω
n

n
v
H
P P
=
n
v
X
i=1
p
2
2
− W (i)
+
n
v
X
i>j
1
r
ij
W
W
γ
W =
X
γ
W
γ
W
γ
φ
v
f
fφ
v
= ǫ
v
φ
v
f =
p
2
2
−
Q
r
+ J − K
J K
W
γ
4s
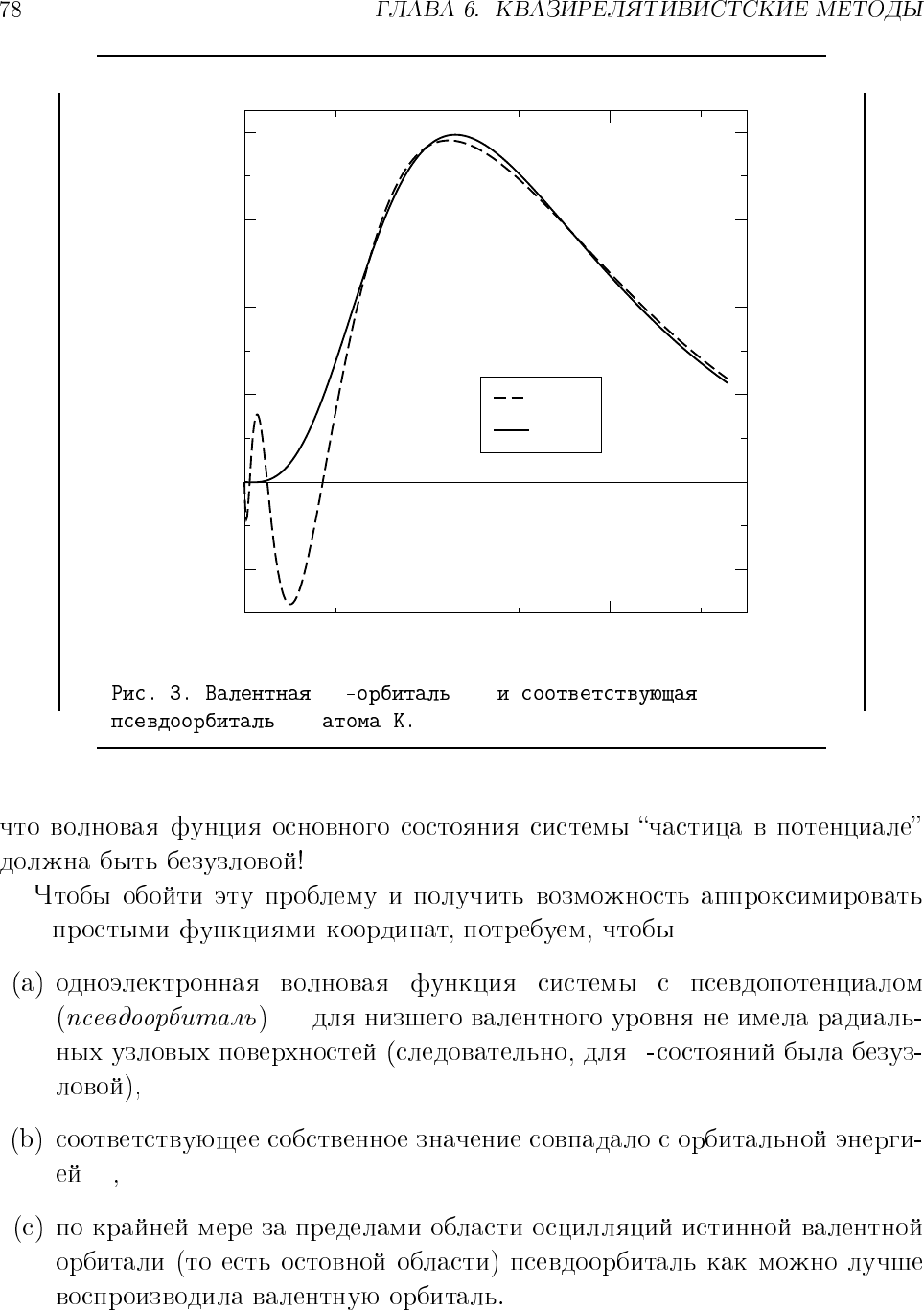
'
&
$
%
0 2
4
r, A
-0.02 0 0.02 0.04 0.06 0.08
r φ(r)
r
~
φ(r)
4s φ
v
e
φ
v
W
γ
e
φ
v
s
ǫ
v

e
φ
v
W
γ
W
γ
= W
γ
(r) =
ǫ
v
− p
2
/2
e
φ
v
(r)
e
φ
v
(r)
W
γ
(r)
ns
n > 4
3d
4f 5g 4p
