Зайцевский А.В. Релятивистская теория электронного строения молекул
Подождите немного. Документ загружается.


α
g
G
12
= −
(α
1
, α
2
)
r
12
.
D
Ψ
+
i
(1)Ψ
+
j
(2) |g
12
|Ψ
+
k
(1)Ψ
−
l
(2)
E
,
D
Ψ
+
i
(1)Ψ
+
j
(2) |g
12
|Ψ
−
l
(1)Ψ
+
k
(2)
E
,
Λ
+

{Ψ
+
i
}
Λ
+
=
X
i
Z
|Ψ
+
i
ihΨ
+
i
|
Λ
+
= Λ
+
(1)Λ
+
(2)
Λ
+
Ψ
+
i
(1)Ψ
−
j
(2) = Λ
+
Ψ
−
j
(1)Ψ
+
i
(2) = 0
g
np
12
= Λ
+
g
12
Λ
+
g
12
g
np
12
n
H
DC
H
DCB
H
np
DC
=
X
j
H
D
(j) +
X
j>k
g
C,np
jk
, H
np
DCB
= H
DC
+
X
j>k
(g
B,np
jk
)

Ψ =⇒ Ψ
′
=
ψ
LL
cψ
LS
cψ
SL
c
2
ψ
SS
.
H
′
=
V (σ
2
, p
2
) (σ
1
, p
1
) 0
λV − 2 0 λ(σ
1
, p
1
)
λV − 2 λ(σ
2
, p
2
)
··· λ
2
V − 4λ
S =
1
λ
λ
λ
2
λ = c
−2
H
′
S
λ
H
′
= H
′
0
+ λ H
′
1
+ λ
2
H
′
2
H
′
0
=
V (σ
2
, p
2
) (σ
1
, p
1
) 0
−2 0 0
−2 0
··· 0
, H
′
1
=
0 0 0 0
V 0 (σ
1
, p
1
)
V (σ
2
, p
2
)
··· −4
,
H
′
2
=
0 0 0 0
0 0 0
0 0
··· V

S = S
0
+ λS
1
+ λ
2
S
2
=
1
0
0
0
+ λ
0
1
1
0
+ λ
2
0
0
0
1
λ
(H
′
0
+ λH
′
1
+ λH
′
2
) (Ψ
′
0
+ λΨ
′
1
+ . . .)
= (E
0
+ λE
1
+ . . .)
S
0
+ λS
1
+ λ
2
S
2
(Ψ
′
0
+ λΨ
′
1
+ . . .)
λ = 0
V ψ
′
0LL
+ (σ
2
, p
2
)ψ
′
0LS
+ (σ
1
, p
1
)ψ
′
0SL
= E
0
ψ
′
0LL
(σ
2
, p
2
)ψ
′
0LL
− 2ψ
′
0LS
= 0
(σ
1
, p
1
)ψ
′
0LL
− 2ψ
′
0SL
= 0
ψ
′
0LS
ψ
′
0SL
ψ
′
0LL
ψ
′
0SS
E
1
= hΨ
′
0
|H
1
− E
0
S
1
|Ψ
′
0
i
=
*
Ψ
′
0
0 0 0 0
0 V − E
0
0 (σ
1
, p
1
)
0 0 V −E
0
(σ
2
, p
2
)
0 (σ
1
, p
1
) (σ
2
, p
2
) −4
Ψ
′
0
+
= hψ
′
0LS
|V − E
0
|ψ
′
0LS
i + hψ
′
0SL
|V − E
0
|ψ
′
0SL
i
+ hψ
′
0LS
|(σ
1
, p
1
)|ψ
′
0SS
i + hψ
′
0SS
|(σ
1
, p
1
)|ψ
′
0LS
i
+ hψ
′
0SL
|(σ
2
, p
2
)|ψ
′
0SS
i + hψ
′
0SS
|(σ
2
, p
2
)|ψ
′
0SL
i − 4 hψ
′
0SS
|ψ
′
0SS
i
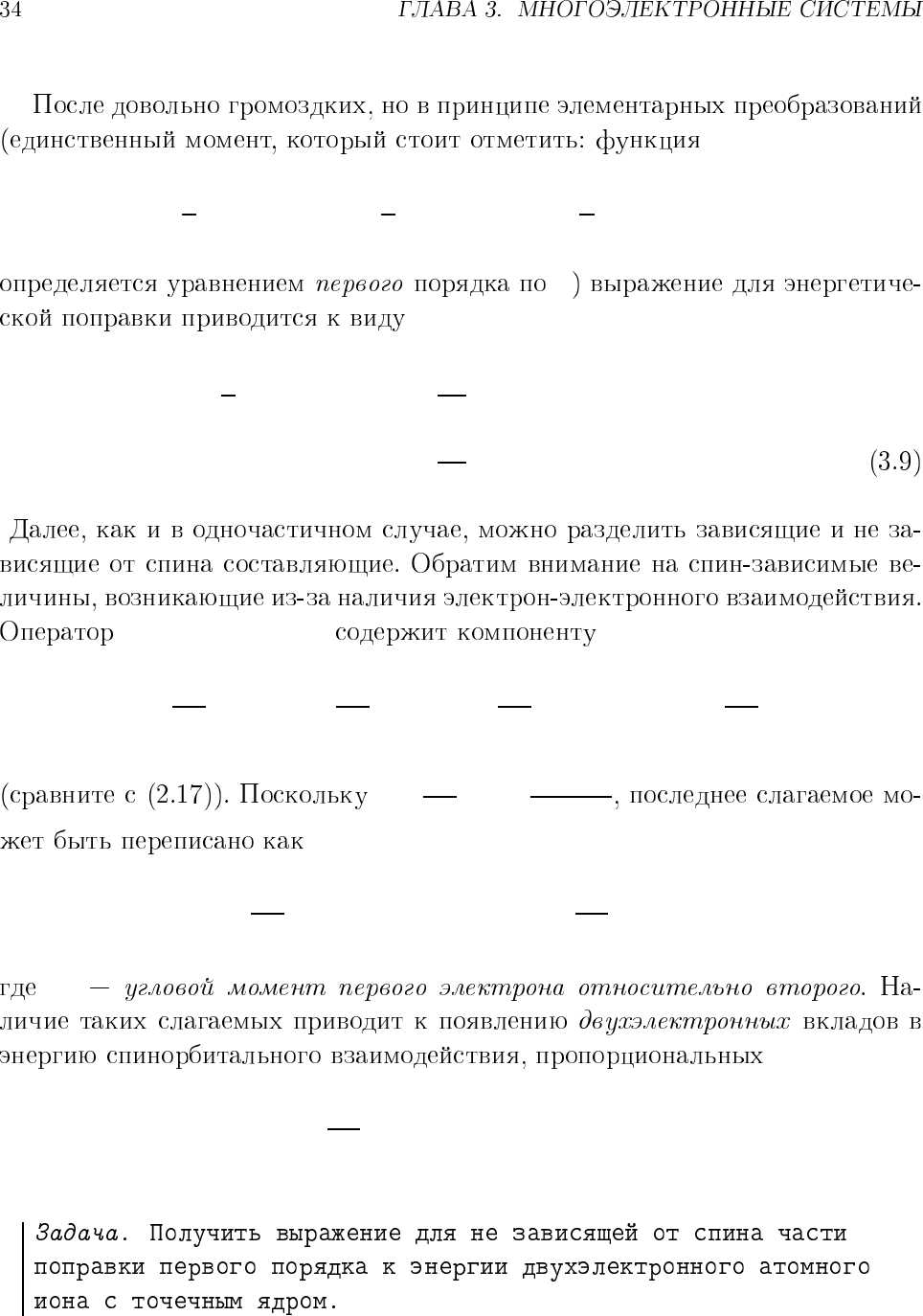
ψ
′
0SS
ψ
′
0SS
=
1
2
(σ
2
, p
2
)ψ
′
0SL
=
1
2
(σ
1
, p
1
)ψ
′
0LS
=
1
4
(σ
1
, p
1
)(σ
2
, p
2
)ψ
′
0LL
λ
E
1
=
1
4
hψ
′
0LL
| (σ
2
, p
2
) (
p
2
1
2
+ V − E
0
)(σ
2
, p
2
)
+ (σ
1
, p
1
) (
p
2
2
2
+ V − E
0
)(σ
1
, p
1
) |ψ
′
0LL
i
(σ
1
, p
1
)V (σ
1
, p
1
)
(σ
1
, p
1
)
1
r
12
(σ
1
, p
1
) =
1
r
12
p
2
1
− i((∇
1
1
r
12
), p
1
) + (σ
1
, (∇
1
1
r
12
) × p
1
)
(∇
1
1
r
12
) = −
r
1
− r
2
r
3
12
−
1
r
3
12
(σ
1
, (r
1
− r
2
) × p
1
) = −
2
r
3
12
(s
1
, l
12
)
l
12
*
ψ
0LL
1
r
3
12
((s
1
, l
12
) + (s
2
, l
21
))
ψ
0LL
+
.

g
G
12
λ
0 0 0 b
0 0 b 0
0 b 0 0
b 0 0 0
, b = −
(σ
1
, σ
2
)
r
12
E
1

r =⇒ r
p =⇒ −p
l =⇒ −l
s =⇒ −s
σ/2
K
tr

−i∇
−ir × ∇
σ
y
= 2s
y
σ
x
σ
z
K : KΨ = Ψ
∗
p
−p l −l s
y
−s
y
s
x
s
z
K s
x
s
z
σ
y
σ
y
σ
x
σ
−1
y
= σ
y
σ
x
σ
y
= iσ
y
σ
z
= −σ
x
σ
z
σ
y
K i
iσ
y
=
0 1
−1 0
s
x
s
z
K
tr
= iσ
y
K.
K
tr
iσ
y
K
tr
=
iσ
y
0
0 iσ
y
K.
K K
tr
c
µ
c
ν
K(c
µ
Ψ
µ
+ c
ν
Ψ
ν
) = c
∗
µ
KΨ
µ
+ c
∗
ν
KΨ
ν
; K
tr
(c
µ
Ψ
µ
+ c
ν
Ψ
ν
) = c
∗
µ
K
tr
Ψ
µ
+ c
∗
ν
K
tr
Ψ
ν
K
hKΨ
µ
|KΨ
ν
i = hΨ
µ
|Ψ
ν
i
∗
−→ |hKΨ
µ
|KΨ
ν
i| = |hΨ
µ
|Ψ
ν
i|
K
tr
iσ
y

K
tr
K
2
tr
= iσ
y
K(iσ
y
)K = (iσ
y
)
2
K
2
= −1
iσ
y
Φ
K
tr
Φ = kΦ,
k
K
2
tr
Φ = K
tr
kΦ = k
∗
K
tr
Φ = k
∗
kΦ
Φ K
2
tr
k
∗
k = |k|
2
K
2
tr
Ψ = −Ψ
Ψ H
D
K
tr
Ψ H
D
Ψ K
tr
H
D
Ψ K
tr
Ψ
n K
tr
n
x z iσ
yj
, j = 1, ..., n
α
j
σ
j
K
tr
iσ
yj
(−1)
K
2
tr
=
1 n
−1
n.

K
P
0
r =⇒ −r
p =⇒ −p
l =⇒ l
s =⇒ s
V (r) = V (−r)
P
0
P
0
P
0
ψ =
ψ
P
0
ψ = −ψ
V ψ
L
+ (σ, p) ψ
S
= Eψ
L
(σ, p) ψ
L
+ (V − 2c
2
)ψ
S
= Eψ
S
ψ
L
ψ
S
H
D
P
P = P
0
β
