Зайцевский А.В. Релятивистская теория электронного строения молекул
Подождите немного. Документ загружается.


i
ii
p × A =
1
i
(∇× A) −
1
i
A × ∇ =
1
i
H − A × p
s
1
2c
(σ, H ) =
1
c
(s, H)
s/c
H
λ λ
H
′
S
E = E
0
+ λE
1
+ λ
2
E
2
+ ...
Ψ
′
= Ψ
′
0
+ λΨ
′
1
+ λ
2
Ψ
′
2
+ ...
λ
E
k
Ψ
′
k
(H
′
0
+ λH
′
1
) (Ψ
′
0
+ λΨ
′
1
+ . . .)
= (E
0
+ λE
1
+ . . .) (S
0
+ λS
1
) (Ψ
′
0
+ λΨ
′
1
+ . . .)
λ
k
k = 0, 1, 2...
λ k = 0
F
F
(∇F ) F ∇F
F

λ
H
′
1
Ψ
′
0
+ H
′
0
Ψ
′
1
= E
1
S
0
Ψ
′
0
+ E
0
S
1
Ψ
′
0
+ E
0
S
0
Ψ
′
1
Ψ
′
0
H
′
0
S
0
hΨ
′
0
|(H
′
0
− E
0
S
0
) = 0,
hΨ
′
0
|H
′
0
− E
0
S
0
|Ψ
′
1
i = 0,
hΨ
′
0
|H
′
1
|Ψ
′
0
i = E
1
hΨ
′
0
|S
0
|Ψ
′
0
i
+ E
0
hΨ
′
0
|S
1
|Ψ
′
0
i
ψ
′
0L
E
1
= hΨ
′
0
|H
′
1
− E
0
S
1
|Ψ
′
0
i =
*
ψ
′
0L
ψ
′
0S
0 0
0 V −E
0
ψ
′
0L
ψ
′
0S
+
= hψ
′
0S
|V −E
0
|ψ
′
0S
i,
E
1
=
1
4
hψ
′
0L
|(σ, p)( V −E
0
)(σ, p)|ψ
′
0L
i
ψ
′
0L
σ
(σ, p)V = V (σ, p) − i (σ, (∇V ))
(σ, p)V (σ, p) = V p
2
− i (σ, (∇V )) (σ, p)
= V p
2
− i ((∇V ), p)
+ (σ, (∇V ) × p)

∆V = V ∆ + 2 ((∇V ), ∇) + (∆V ),
∇ = ip
−p
2
V = −V p
2
+ 2i ((∇V ), p) + (∆V ),
−i ((∇V ), p) =
1
2
(∆V ) +
1
2
(p
2
V −V p
2
)
(σ, p)V (σ, p) =
1
2
(∆V ) + p
2
V + V p
2
+ (σ, (∇V ) × p) .
E
1
= E
SC
+ E
SO
,
E
SC
=
1
8
D
ψ
′
0L
(∆V ) + p
2
V + V p
2
− 2E
0
p
2
ψ
′
0L
E
E
SO
=
1
4
hψ
′
0L
|(σ, (∇V ) × p)|ψ
′
0L
i
E
SC
E
SO
V = V (r)
∂V
∂z
=
∂V
∂r
∂r
∂z
=
z
r
∂V
∂r
, (∇V ) =
r
r
∂V
∂r
E
SO
G
SO
G
SO
=
1
4
(σ, (∇V ) × p) =
1
4r
∂V
∂r
(σ, r × p) =
1
2r
∂V
∂r
(s, l)
l

ψ
′
0L
(V − E
0
)ψ
′
0L
= −
1
2
p
2
ψ
′
0L
D
ψ
′
0L
(p
2
V + V p
2
− 2E
0
p
2
ψ
′
0L
E
= −
D
ψ
′
0L
p
4
ψ
′
0L
E
.
E
SC
E
SC
= E
MV
+ E
D
,
E
MV
= −
*
ψ
′
0L
p
4
8
ψ
′
0L
+
E
D
=
*
ψ
′
0L
(∆V )
8
ψ
′
0L
+
.
E
MV
c
−2
E = (c
2
p
2
+ c
4
)
1/2
= c
2
1 +
p
2
c
2
1/2
= c
2
+
p
2
2
−
p
4
8c
2
+ . . .
c
−2
E
MV
E
D
̺
(∆V ) = −( ∆ϕ) = 4π̺
E
D
Q
̺(r) = Qδ(r)
r = 0 E
D
=
πQ
2
ψ
′
0L
(0)
†
ψ
′
0L
(0)

E
1
ψ
′
1L
ψ
′
1S
ψ
′
1
λ
c
−1
1s
Q
e
−Qr
1
0
ψ
′
0L
= ψ
0L
=
e
−Qr
0
ψ
′
0S
= cψ
0S
=
1
2
(σ, p)ψ
0L
=
1
2i
∂
∂z
∂
∂x
− i
∂
∂y
∂
∂x
+ i
∂
∂y
−
∂
∂z
e
−Qr
0

∂r/∂η = η/r η = x, y z
ψ
′
0S
= −
Q
2i
z
r
e
−Qr
x + iy
r
e
−Qr
p
1p
ψ
′
0S
∼
Q
2
Y
10
√
2Y
11
e
−Qr
,
ψ
′
0S
=
const
1
· 1p
0
const
2
·1p
+
•
ψ
S
≈ c
−1
ψ
′
0S
•
α, β
•
λE
1
Y
10
= i
v
u
u
t
3
4π
z
r
, Y
11
= −i
v
u
u
t
3
8π
x + iy
r
, Y
1,−1
= Y
∗
11
.

c
−1
Ψ
i
=
ψ
iL
ψ
iS
= ψ
iL
1
0
+ ψ
iS
0
1
= ψ
iL
u
L
+ ψ
iS
u
S
.
Ψ
i
(1)Ψ
j
(2) Ψ
u
L
u
S
u
L
(1)u
L
(2)=
1
0
0
0
, u
L
(1)u
S
(2)=
0
1
0
0
, u
S
(1)u
L
(2)=
0
0
1
0
, u
S
(1)u
S
(2)=
0
0
0
1
.

Ψ(1, 2) = ψ
LL
1
0
0
0
+ ψ
LS
0
1
0
0
+ ψ
SL
0
0
1
0
+ ψ
SS
0
0
0
1
=
ψ
LL
ψ
LS
ψ
SL
ψ
SS
.
H = H
D
(1) + H
D
(2), H
D
(1) = c(α
1
, p
1
) + V (1) + c
2
(β − 1)
1
,
H
D
(2) = c(α
2
, p
2
) + V (2) + c
2
(β − 1)
2
.
α (β − 1)
α
1
=
0 0 σ
1
0
0 0 0 σ
1
σ
1
0 0 0
0 σ
1
0 0
α
2
=
0 σ
2
0 0
σ
2
0 0 0
0 0 0 σ
2
0 0 σ
2
0
(β − 1)
1
=
0 0 0 0
0 0 0 0
0 0 −2 0
0 0 0 −2
, (β − 1)
2
=
0 0 0 0
0 −2 0 0
0 0 0 0
0 0 0 −2
H=
V (1)+V (2) c(σ
2
, p
2
) c(σ
1
, p
1
) 0
V (1)+V (2)−2c
2
0 c(σ
1
, p
1
)
V (1)+V (2)−2c
2
c(σ
2
, p
2
)
··· V (1)+V (2)−4c
2
H
{Ψ
i
} {ǫ
i
}
{Ψ
i
(1)Ψ
j
(2); ǫ
i
+ ǫ
j
}

i 6= j
Ψ
d+
j
(1)Ψ
d+
k
(2)
{ǫ
d+
j
+ ǫ
d+
k
} ǫ
d+
j
, ǫ
d+
k
E
E = ǫ
c+
q
+ ǫ
c−
p
n
2
n
Ψ =
ψ
LL...L
ψ
LL...S
···
ψ
SS...S
3n
n
c
−1
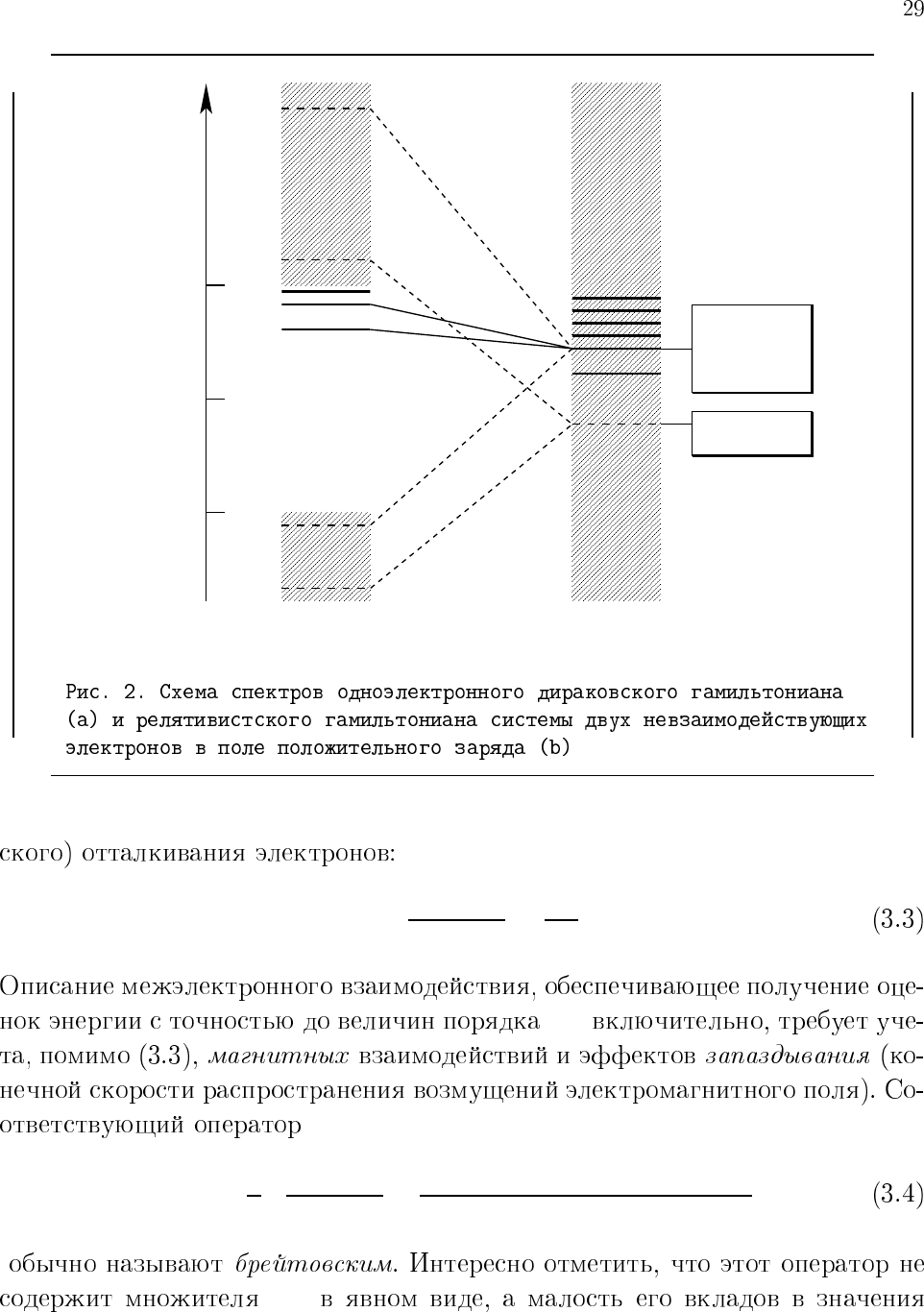
'
&
$
%
2
−2c
2
−c
0
E
(a) (b)
ε
c−
d+
j
ε
d+
k
ε
q
c+
ε
p
ε
d+
k
ε
q
c+
+
+
d+
c−
p
ε
j
ε
=
ε
c+
ε
c−
r
s
. . .
ε
c−
+
ε
s
c+
r
. . .
g
C
12
=
1
|r
1
− r
2
|
=
1
r
12
.
c
−2
g
B
12
= −
1
2
(α
1
, α
2
)
r
12
+
(α
1
, (r
1
− r
2
))(α
2
, (r
1
− r
2
))
r
3
12
c
−2
