Заяц В.Г. Теория механизмов, машин и манипуляторов
Подождите немного. Документ загружается.


21
3.3 Определение приведенного момента
сил сопротивления и приведенного момента
движущихся сил, работы сил сопротивления
3.3.1 Определение сил полезного
(технологического) сопротивления
В рассматриваемой рабочей машине приведенный момент движу-
щих сил принимается постоянным (
Д
П
Μ = const ), а приведенный мо-
мент сил сопротивления
С
П
Μ определяется в результате приведения си-
лы полезного сопротивления
рез
F и сил тяжести звеньев (см. рис. А.1 ).
Сила
рез
F , действующая на рабочий орган, определяется из механиче-
ской характеристики технологического процесса, заданной в виде гра-
фической зависимости
(
)
c
SF
рез
. Для решения динамических задач необ-
ходимо получить зависимости
рез
F от обобщенной координаты
1
ϕ . Для
этого механическую характеристику
(
)
c
SF
рез
привязываем к крайним
положениям механизма. Учитываем, что рабочий ход происходит при
движении ползуна слева направо.
Усилие резания 5005
рез
=F Н.
Усилие холостого хода 55050051,01,0
резхх.
=⋅== FF Н.
Используя разметку хода ползуна (точки C), находим значения силы
рез
F во всех положениях механизма:
,
5ПС FF
уFF µ==
где
F
у — ордината графика
(
)
c
SF
рез
;
F
µ — масштабный коэффициент сил,
мм
Н
, равный
100
55
5005
max
рез
===µ
F
F
у
F
.
Примечание. Результаты определения
5
F
желательно привести в таблице.
PDF created with pdfFactory Pro trial version www.pdffactory.com

22
3.3.2 Определение приведенного момента сопротивления
Величину
С
П
М определяем из равенства мгновенных мощностей,
развиваемых моментом
С
П
М на звене приведения и силами F
5
, G
2
, С
3
,
G
4
, G
s
:
.
5534435ПС1
С
П C
y
S
y
SС
VGVGVGVFМ ±±±=ω
По исходным данным определяем массы звеньев:
7,41877,025
1
=⋅==
ОА
lqm ;
7,208275,025
23
=⋅==
ВО
lqm ;
8,315,025
4
=⋅==
bc
lqm ;
4,417,2022
35
=⋅== mm .
Центральными моментами инерции звеньев являются:
1) момент инерции
1S
I , кг ∙ м
2
,
звена 1, равный
0281,01877,07,417,017,0
22
11
=⋅⋅==
ОАS
lmI ;
2) момент инерции
3S
I , кг ∙ м
2
, звена 3, определяемый следующим
образом
41,28275,07,2017,017,0
22
33
2
=⋅⋅==
ВОS
lmI ;
3) момент инерции
4S
Й , кг ∙ м
2
, звена 4 равный:
0145,015,08,317,017,0
22
44
=⋅⋅==
ВСS
lmЙ .
Силы тяжести звеньев определяются следующим образом:
4681,97,4
11
=⋅== gmG ;
20381,97,20
33
=⋅== gmG ;
PDF created with pdfFactory Pro trial version www.pdffactory.com
23
3781,98,3
44
=⋅== gmG ;
40681,94,41
55
=⋅== gmG .
Учитывая, что сила тяжести
4
G значительно меньше
ПС
F (значение
4
G меньше
ПС
F приблизительно в 149 раз), ее влиянием на
С
П
М пре-
небрегаем. Поскольку силы тяжести
5
G действует перпендикулярно
скорости движения суппорта, то она также не будет влиять на величину
приведенного момента сил сопротивления.
Тогда
.
3351ПС
1
3
3
1
5
ПС
С
П
y
S
y
SC
iGiF
V
G
V
FМ ±=
ω
±
ω
=
Используя таблицу 2.2, вычисляем
С
П
М , Н ∙ м, (например, для поло-
жения 3):
4,12010084,02032034,05005
С
П
=⋅+⋅=М .
Приняв масштабный коэффициент моментов
М
µ ,
мм
мН ⋅
, из условия
10
112
4,1201
max
C
maxП
С
П
===µ
М
М
y
M
,
вычисляем ординаты графика по формуле
М
M
М
y
м
С
П
С
П
= .
Результаты вычислений приведены в таблице 3.1, на основании их
построен график
(
)
1
С
П
ϕМ .
Масштабный коэффициент углов
ϕ
µ , рад / мм, равен
[ ]
0349,0
180
2
120
2
=
π
=
−
π
=µ
ϕ
PDF created with pdfFactory Pro trial version www.pdffactory.com

24
Таблица 3.1 — Определение
приведенного момента сил сопротивления
Номер
положения
С
П
M , Н · м
Д
П
M
y , мм
0 0 0
1 62,1 6,2
2 955,1 95,5
3 1120,4 112
4 1118,8 111,9
5 990,1 99
6 70,0 7
7 21,2 2,1
7’ 0 0
8 74,1 7,4
9 191,5 19,2
10 213,5 21,4
11 95,2 9,5
Отрезок (0 – 12) = 180 соответствует одному циклу установившего-
ся движения (
π
=
°
=
ϕ
2360
ц
рад ).
Приведенный момент движущих сил
Д
П
М принимается постоянным, а
его величина определяется из условия, что за цикл установившегося движе-
ния изменение кинетической энергии машины 0
СД
=
−
=
∆
ААТ Следова-
тельно, работы движущих сил и сил сопротивления равны
(
)
СЦДЦ
АА
=
.
3.3.3 Определение работы сил сопротивления
и работы движущих сил
Так как работа сил сопротивления
∫
ϕ
ϕ
ϕ=
1
0
1
С
П
dМА
С
, то график
(
)
1С
ϕ
А
можно построить путем либо численного, либо графического интегри-
рования зависимости
(
)
1
С
П
ϕМ .
PDF created with pdfFactory Pro trial version www.pdffactory.com

25
Используем численное интегрирование по методу трапеций, соглас-
но которому
,)(5,0
С
Пз
1
С
П1
ϕ∆++=
−
−
ММАА
i
СiСi
(3.2)
где
ϕ
∆
— шаг интегрирования, равный
12
2
1
π
=ϕ∆
= 0,5236.
Формула (3.2) применяется последовательно от интервала к интервалу:
0
0
=
С
А ;
(
)
(
)
3,165236,01,6205,005,0
1
С
1П
С
0П0С1С
=++=ϕ∆++= ММАА ;
(
)
(
)
;6,2825236,01,9551,625,03,165,0
1
С
П2
С
П11С2С
=++=ϕ∆++= ММАА
(
)
(
)
;9,8255236,04,11201,9555,06,2825,0
1
С
П3
С
П2С2С3
=++=ϕ∆++= ММАА
(
)
(
)
;1,41215236,08,11184,11205,09,8255,0
1
С
П4
С
П3С3С4
=++=ϕ∆++= ММАА
(
)
(
)
;4,96415236,01,9904,11185,01,14125,0
1
С
П5
С
П4С4С5
=++=ϕ∆++= ММАА
(
)
(
)
;8,24125236,0701,9905,03,19645,0
1
С
П6
С
П556
=++=ϕ∆++= ММАА
СС
(
)
(
)
;7,26525236,02,21705,08,22415,0
1
С
П7
С
П6С6С7
=++=ϕ∆++= ММАА
(
)
(
)
;6,29025236,01,742,215,07,22655,0
1
С
П8
С
П7С7С8
=++=ϕ∆++= ММАА
(
)
(
)
;2,36025236,05,1911,745,06,22905,0
1
С
П9
С
П8С8С9
=++=ϕ∆++= ММАА
(
)
(
)
;2,46625236,05,2135,1915,02,23605,0
1
С
П10
С
П9С9С10
=++=ϕ∆++= ММАА
(
)
(
)
;54725236,02,955,2135,02,24665,0
1
С
П11
С
П10С10С11
=++=ϕ∆++= ММАА
(
)
(
)
.57225236,002,955,025475,0
1
С
П12
С
П11С11С12
=++=ϕ∆++= ММАА
PDF created with pdfFactory Pro trial version www.pdffactory.com

26
Таким образом, работа сил сопротивления за цикл
СЦ
А , Дж, равна
2572
СЦ12СЦ
== АА Дж.
Принимаем масштабный коэффициент 30=µ
А
Дж / мм, вычисляем
и откладываем ординаты графика
(
)
1
ϕ
С
А
А
С
Ас
А
У
µ
= .
Строим график
(
)
1
ϕ
С
А (рис. А.3). Результаты вычислений заносим в
таблицу 3.2.
Таблица 3.2 — Определение работы сил сопротивления
Номер положения
С
А , Дж
АС
у , мм
0 0 0
1 16,3 0,54
2 282,6 9,4
3 825,9 27,5
4 1412,2 47,1
5 1964,3 65,5
6 2241,8 74,7
7 2265,7 75,5
8 2290,6 76,4
9 2360,2 78,7
10 2466,2 82,2
11 2547 84,9
12 2571,9 85,7
Примечание. Метод графического дифференцирования подробно изложен в источ-
никах [1], [8], [9].
3.3.4 Определение приведенного момента движущих сил
Так как работа движущих сил за цикл
π= 2
Д
ПДС
МА
, то приведенный
момент движущих сил
Д
П
М равен
6,409
14,32
5722
22
СЦДЦ
Д
П
=
⋅
=
π
=
π
=
АА
М .
PDF created with pdfFactory Pro trial version www.pdffactory.com

27
Ордината графика
Д
П
М = const и равна
41
10
6,409
М
Д
П
Д
П
==
µ
=
М
М .
3.4 Определение переменной составляющей
приведенного момента инерции
Величина
II
П
I определяется из равенства кинетической энергии звена
приведения с моментом инерции
II
П
I и суммы кинетических энергий
звеньев с переменными передаточными функциями. Такими звеньями яв-
ляются звенья 3, 4 и 5 исполнительного рычажного механизма. Тогда име-
ем равенство
.
2
2
2
2
2
2
5
2
44
2
44
2
3
2
1
II
П
2
СSS
О
VmVmI
I
I
++
ω
+
ω
=
ω
Откуда
dcва
V
m
V
mIII
СS
SО
+++=
ω
+
ω
+
ω
ω
+
ω
ω
=
2
1
5
2
1
4
4
2
1
4
4
2
1
3
II
П
2
,
где
2
31
2
iа
О
Ι= ;
2
41
4
iIb
S
=
;
2
4
41
S
imc =
2
515
imd = .
Момент инерции
2
О
Ι
,
2
м
кг
⋅
, звена 3 относительно оси вращения
О
2
равен
954,54138,07,2041,2
22
33
322
=⋅+=+=
SОSО
lmII
.
Масштабный коэффициент
1
µ ,
мм
мкг
2
⋅
, равен
1,0
1,84
411,8
max
II
maxП
1
===µ
ι
y
I
.
PDF created with pdfFactory Pro trial version www.pdffactory.com
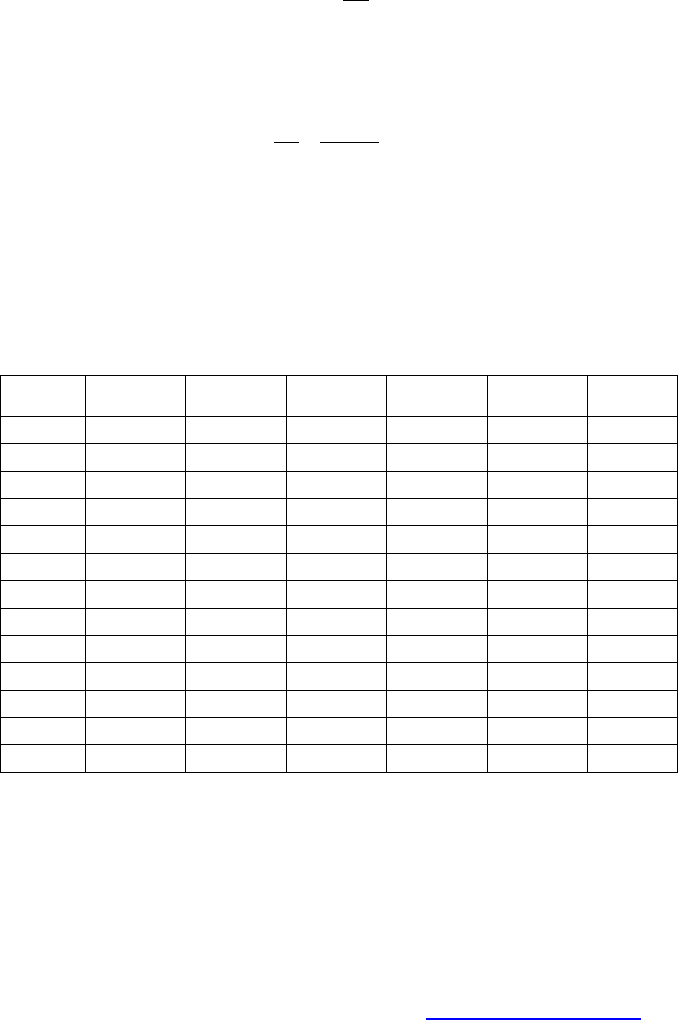
28
Вычисляем ординаты графика:
Ι
Ι
µ
=
II
П
I
у
.
Для положения 3 имеем
4,22
1,0
2354,2
II
П
==
µ
=
Ι
Ι
I
у
.
Результаты определения
II
П
I приведены в таблице 3.3, на основании
их построен график
(
)
1
II
П
ϕI (см. рис. А.3).
Таблица 3.3 — Определение переменной составляющей приведенного момента
инерции
Номер
положения
а
,
⋅
2
кгм
b,
⋅
2
кгм
с
,
⋅
2
кгм
d ,
⋅
2
кгм
II
П
I ,
⋅
2
кгм
1
y ,
мм
0 0 0 0 0 0 0
1 0,11516 0,00074 0,04581 0,47386 0,63558 6,4
2 0,2671 0,00082 0,11399 1,24804 1,62995 16,3
3 0,35435 0,00019 0,15567 1,72519 2,2354 22,4
4 0,36619 5,9E-05 0,15876 1,72859 2,2536 22,5
5 0,30028 0,00065 0,1267 1,3601 1,78774 17,9
6 0,16407 0,0009 0,06864 0,751 0,98462 9,8
7 0,0148 0,00012 0,00626 0,0701 0,09128 0,9
7’ 0 0 0 0 0 0
8 0,14514 0,00102 0,0611 0,67682 0,88408 8,8
9 1,04805 0,00198 0,44342 4,76397 6,25742 62,5
10 1,33221 0,00082 0,58571 6,49307 8,41181 84,1
11 0,32686 0,00188 0,13231 1,39649 1,85755 18,6
PDF created with pdfFactory Pro trial version www.pdffactory.com

29
3.5 Определение постоянной составляющей
приведенного момента инерции
и момента инерции маховика
Путем графического вычитания ординат работ А
Д
и А
С
строим
график изменения кинетической энергии машины
СД
ААТ −=∆
(см. рис. А.3).
Масштабный коэффициент 30=µ=µ
ΑΤ
Дж / мм.
Определение
I
П
I производим методом Виттенбауэра, так как
δ
>
04
0
,
.
Примечание. Метод Мерцалова представлен в [3; 5; 8].
По методу Виттенбауэра на основании ранее построенных графиков
(
)
ϕ∆Τ и
(
)
ϕ
ΙΙ
П
I
необходимо построить диаграмму энергомасс
(
)
.I
ΙΙ
∆Τ
П
(см. рис. А.3).
Диаграмма энергомасс (диаграмма Виттенбауэра) строится путем
графического исключения параметра
ϕ
(угла поворота кривошипа) из
графиков изменения кинетической энергии механизма и приведенного
момента инерции.
Для определения момента инерции маховика по заданному коэффици-
енту неравномерности движения
δ
следует провести касательные к гра-
фику энергомасс под углами
max
ψ и
min
ψ к оси абсцисс (оси приведенного
момента инерции), тангенсы которых определяются по формулам
( ) ( )
;203576,0055,0176,10
302
1,0
1
2
tg
22
1max
=+
⋅
=δ+ω
µ
µ
=ψ
Τ
I
( ) ( )
22
min1
0,1
tg110,7610,0550,18235.
2230
I
Τ
µ
ψ=ω−δ=−=
µ⋅
Производя необходимые вычисления, получим
maxmin
11,507;10,33.
ψ=ψ=
oo
PDF created with pdfFactory Pro trial version www.pdffactory.com

30
Постоянную составляющую приведенного момента инерции
I
П
I на-
ходим из выражения
(
)
(
)
δωµ=
Τ
2
1
I
П
/abI ,
где ab — отрезок, отсекаемый проведенными касательными на оси ор-
динат диаграммы энергомасс, равный 39,6 мм.
Тогда
I
П
I , кг ∙ м
2
,
равна
(
)
( )
I
П
2
2
1
39,630
186,6.
(10,760,055)
ab
I
Τ
µ
⋅
===
⋅
ωδ
Вычисляем приведенный момент инерции
I
П
I всех вращающихся
звеньев (без маховика) и сравниваем с
I
П
I . Из условия равенства кине-
тических энергий имеем
.4,00281,02,250281,02,20281,02,252,2
000
0
П
=⋅⋅+⋅+=⋅++= IIII
Так как
I
П
I >
0
П
I , то требуется установка дополнительной вра-
щающейся массы в виде маховика, момент инерции
М
I ,
2
м
кг
⋅
,
которогo при установке на кривошипном валу равен
2,1864,06,186
0I
М
=−=−=
ΠΠ
III .
3.6 Определение закона движения звена приведения
Угловую скорость
ω
, рад / с, для любого положения механизма мож-
но найти по формуле
i
I
Т
ψ
µ
µ
=ω tg2 ,
где
i
ψ
— угол наклона прямой, соединяющей точку начала координат с
точкой для соответствующего положения на диаграмме энер-
гомасс относительно оси абсцисс.
PDF created with pdfFactory Pro trial version www.pdffactory.com
