Засєкіна Т.М. Фізика. 10 клас. Профільний рівень
Подождите немного. Документ загружается.

51
ʳíåìàòèêà ïîñòóïàëüíîãî òà îáåðòàëüíîãî ðóõ³â ìàòåð³àëüíî¿ òî÷êè
Îäèíèöÿ ïðèñêîðåííÿ – ìåòð çà ñåêóíäó â êâàäðàò³, [a] = 1 ì/ñ
2
.
Îñê³ëüêè ïðèñêîðåííÿ õàðàêòåðèçóº ñòð³ìê³ñòü çì³íè øâèäêîñò³ ò³ëà ï³ä
÷àñ éîãî íåð³âíîì³ðíîãî ðóõó, à ñàìà øâèäê³ñòü õàðàêòåðèçóº ñòð³ìê³ñòü çì³íè
ïîëîæåííÿ (êîîðäèíàòè) ò³ëà, òî ö³ âåëè÷èíè ïåâíèì ÷èíîì ïîâ’ÿçàí³ îäíà ç
îäíîþ.
Âèðàç
∆υ
∆
r
t
õàðàêòåðèçóº ñåðåäíþ çà ÷àñ ∆t ñòð³ìê³ñòü çì³íè øâèäêîñò³
ðóõó ìàòåð³àëüíî¿ òî÷êè. Öå íàçèâàþòü ñåðåäí³ì ïðèñêîðåííÿì.
ßêùî çìåíøóâàòè ³íòåðâàë ÷àñó, çà ÿêèé çì³íþºòüñÿ øâèäê³ñòü, òî, ÷èì
ìåíøèì áóäå öåé ³íòåðâàë
∆→0t , òèì ìåíøîþ áóäå çì³íà øâèäêîñò³ ∆υ→
r
0 ,
à äð³á
∆υ
∆
r
t
ïðÿìóº äî äåÿêîãî ãðàíè÷íîãî çíà÷åííÿ. Öþ ãðàíèöþ íàçèâàþòü
ìèòòºâèì ïðèñêîðåííÿì òî÷êè ó ïåâíèé ìîìåíò ÷àñó:
∆→
∆υ
′
==υ
∆
r
r
v
0
lim
t
a
t
.
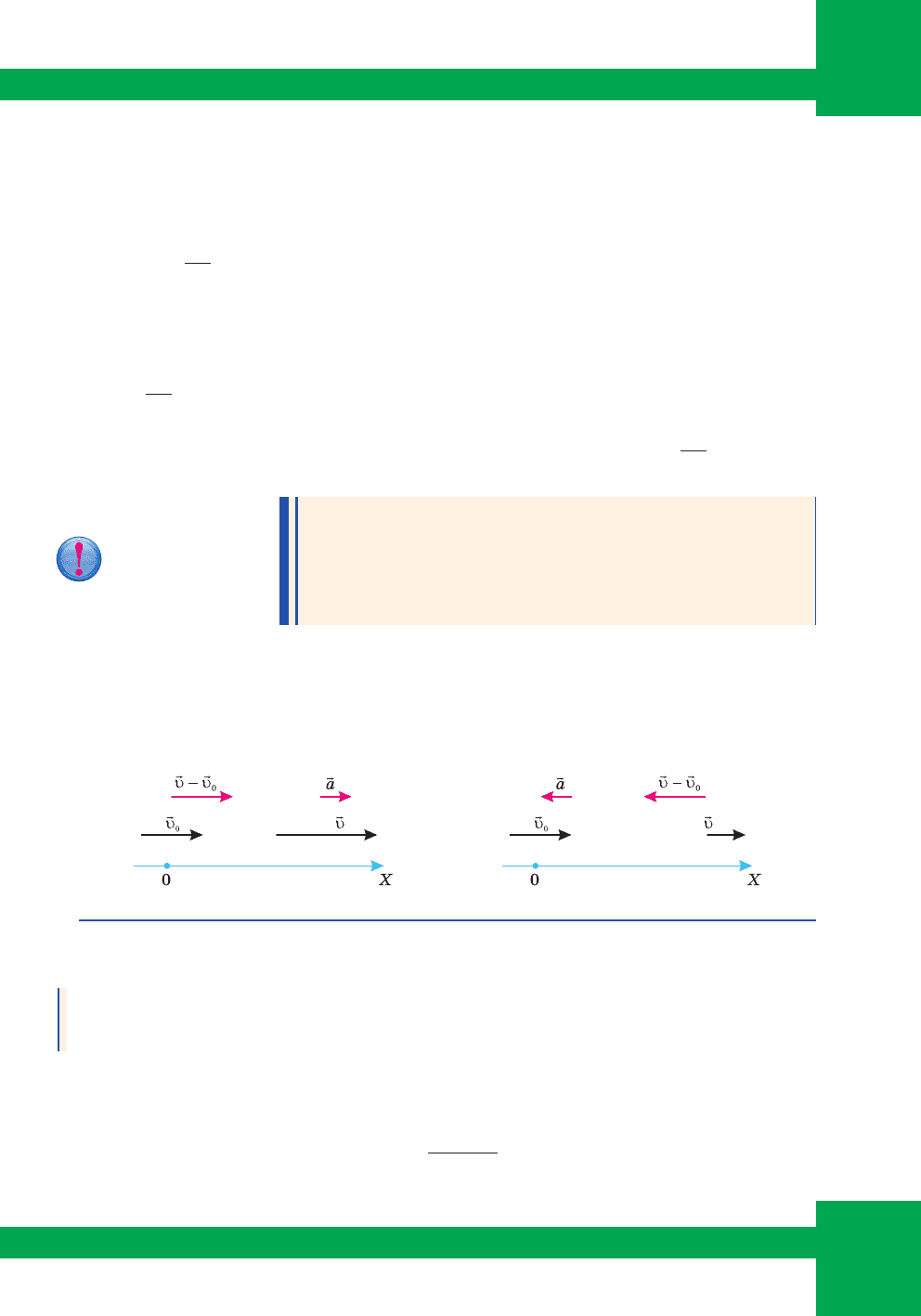
Ðóõ ò³ëà, ïðè ÿêîìó çà áóäü-ÿê³ îäíàêîâ³ ³íòåðâà-
ëè ÷àñó øâèäê³ñòü ðóõó ò³ëà çì³íþºòüñÿ îäíàêîâî,
òîáòî ïðèñêîðåííÿ ï³ä ÷àñ ðóõó ò³ëà çàëèøàºòüñÿ
âåñü ÷àñ ñòàëèì çà íàïðÿìîì ³ ÷èñëîâèì çíà÷åí-
íÿì:
r
a
= const, íàçèâàºòüñÿ ð³âíîïðèñêîðåíèì.
гâíîïðèñêîðåíèé ïðÿìîë³í³éíèé ðóõ.
гâíîïðèñêîðåíèé ïðÿìîë³í³é-
íèé ðóõ ìîæå áóòè âëàñíå ïðèñêîðåíèì, ÿêùî øâèäê³ñòü ò³ëà ç ÷àñîì çðîñòàº
(ìàë. 44) ³ âåêòîðè
υυ
rr
r
0
,,a íàïðàâëåí³ â îäèí á³ê, ³ ñïîâ³ëüíåíèì, ÿêùî øâèä-
ê³ñòü ñïàäຠ(ìàë. 45) ³ âåêòîð
r
a
íàïðàâëåíèé ïðîòèëåæíî äî âåêòîð³â
υυ
rr
0
, .
Çâåðí³òü óâàãó! Ó ïîñ³áíèêàõ ç ô³çèêè ³ â çàäà÷àõ âæèâàþòü ò³ëüêè òåðì³í
«ð³âíîïðèñêîðåíèé ðóõ», çâàæàþ÷è íà òå, ùî ð³âíîñïîâ³ëüíåíèé ðóõ â³äð³çíÿ-
ºòüñÿ çíàêîì ïðîåêö³¿ âåêòîðà ïðèñêîðåííÿ.
Çíà÷åííÿ ïðèñêîðåííÿ ðóõó âèçíà÷àºòüñÿ, âèõîäÿ÷è ç âåêòîðíèõ âëàñòè-
âîñòåé ö³º¿ ô³çè÷íî¿ âåëè÷èíè. Çîêðåìà, ó ïðîåêö³ÿõ íà â³ñü Õ ìàòèìåìî âèðàç
äëÿ ïðèñêîðåííÿ:
υ−υ
=
0xx
x
a
t
.
Ìàë. 44. Ïðèñêîðåíèé ðóõ Ìàë. 45. Ñïîâ³ëüíåíèé ðóõ
52
Ð Î Ç Ä ² Ë 1
Ó âèïàäêó ïðèñêîðåíîãî ðóõó a
x
> 0, îñê³ëüêè øâèäê³ñòü ðóõó çá³ëüøóºòü-
ñÿ, îòæå, υ
x
− υ
0x
> 0 ³ âåêòîð ïðèñêîðåííÿ çá³ãàºòüñÿ ç íàïðÿìîì ðóõó.
ßêùî ðóõ ñïîâ³ëüíåíèé ³ øâèäê³ñòü ç ÷àñîì çìåíøóºòüñÿ (υ
x
− υ
0x
< 0, a
x
< 0),
òî é âåêòîð ïðèñêîðåííÿ íàïðàâëåíèé ïðîòèëåæíî äî íàïðÿìó ðóõó.
Ïðîòå ñë³ä ïàì’ÿòà-
òè, ùî çíàê ïðîåêö³¿ ïðè-
ñêîðåííÿ ùå çàëåæèòü â³ä
âèáîðó ñèñòåìè â³äë³êó.
Ó öüîìó ëåãêî ïåðåêî-
íàòèñü, ÿêùî ðîçãëÿíóòè
âèïàäîê, êîëè îáèäâà ò³ëà
ðóõàþòüñÿ, íàïðèêëàä,
ð³âíîïðèñêîðåíî, àëå ó
ïðîòèëåæíèõ íàïðÿìàõ
(ìàë. 46).
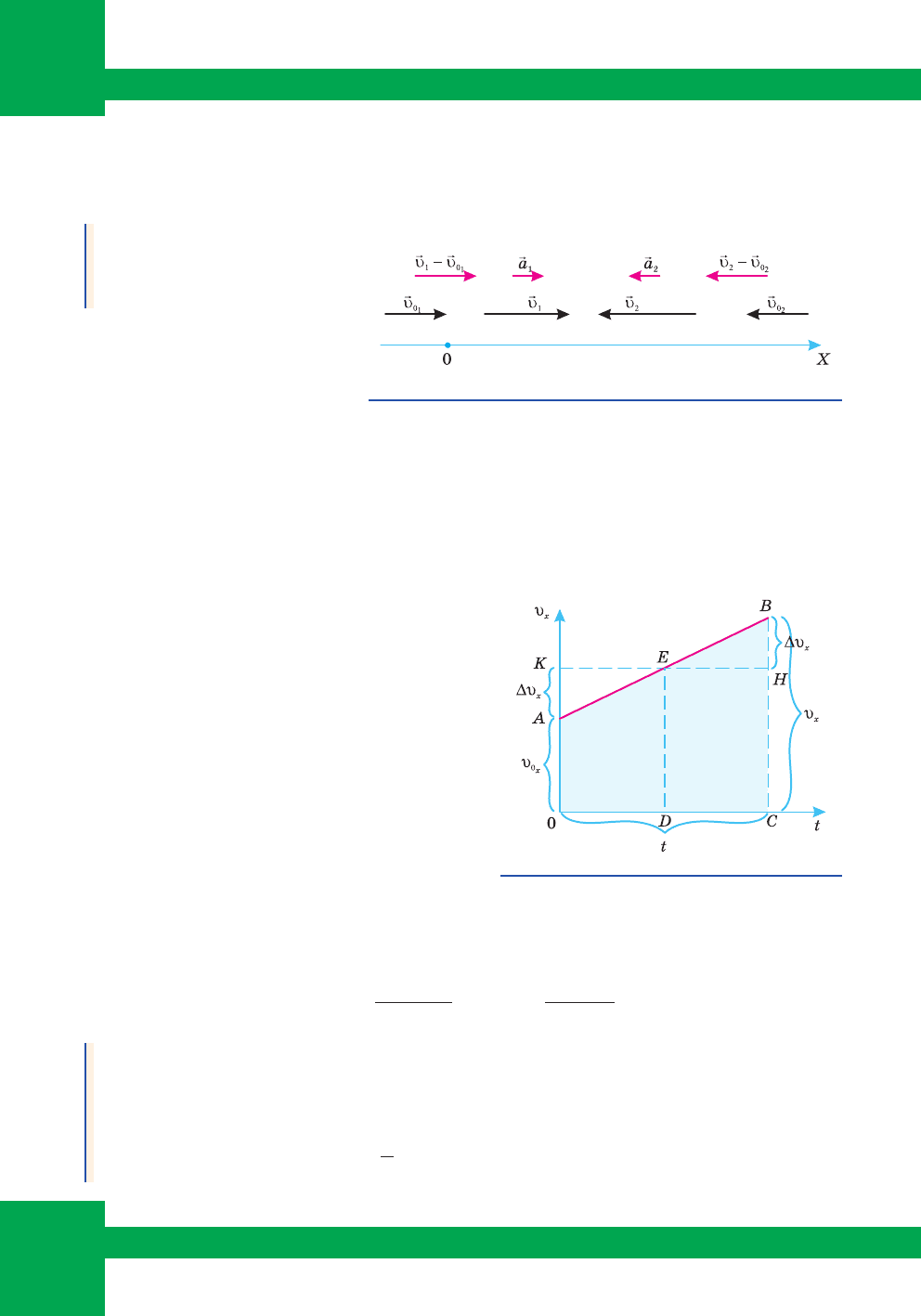
Øâèäê³ñòü ³ ïåðåì³ùåííÿ ð³âíîïðèñêîðåíîãî ðóõó. ²ç ôîðìóë äëÿ ïðèñêî-
ðåííÿ ëåãêî îòðèìàòè ê³íåìàòè÷íå ð³âíÿííÿ øâèäêîñò³ äëÿ ð³âíîïðèñêîðå-
íîãî ðóõó:
υ=υ +
rr
r
0
at àáî â ïðîåêö³ÿõ íà îáðàíó â³ñü Õ: υ=υ +
xoxx
at.
Ïîáóäóºìî ãðàô³ê ð³âíîïðèñêî-
ðåíîãî ðóõó (ìàë. 47), ð³âíÿííÿ ÿêîãî
υ=υ +
xoxx
at.
Ãðàô³ê øâèäêîñò³ ðóõó – ïðÿìà ÀÂ,
â³äð³çêè êîîðäèíàò ÎÀ ³ ÎÑ ðàçîì ç îð-
äèíàòîþ ê³íöåâî¿ øâèäêîñò³ óòâîðþþòü
òðàïåö³þ ÎÀÂÑ. Ïðîâåäåìî â ö³é òðà-
ïåö³¿ ñåðåäíþ ë³í³þ DÅ. ×åðåç òî÷êó Å
ïðîâåäåìî â³äð³çîê ÊÍ, ïàðàëåëüíèé îñ³
÷àñó. Ç ìàëþíêà âèäíî, ùî øâèäê³ñòü ó
òî÷ö³ Å á³ëüøà â³ä ïî÷àòêîâî¿ øâèäêîñò³
υ
0x
íà ∆υ
x
³ íà ∆υ
x
ìåíøà â³ä ê³íöåâî¿
øâèäêîñò³
υ
x
.
Îòæå, ó òî÷ö³ Å ñåðåäíÿ øâèäê³ñòü υ
c
çà ÷àñ ðóõó t.
Ç êóðñó ãåîìåò𳿠â³äîìî, ùî ñåðåäíÿ
ë³í³ÿ òðàïåö³¿ äîð³âíþº ï³âñóì³ îñíîâ:
+
=
2
OA BC
ED
, àáî
υ+υ
υ=
0
2
xx
c
.
Òîáòî äëÿ ð³âíîïðèñêîðåíîãî ðóõó ñåðåäíÿ øâèäê³ñòü âèçíà÷àºòüñÿ ÿê
ñåðåäíº àðèôìåòè÷íå.
ϳäêðåñëèìî, öÿ ôîðìóëà ñïðàâåäëèâà ò³ëüêè äëÿ âèïàäêó ð³âíîïðèñêî-
ðåíîãî ðóõó, ó âèïàäêó äîâ³ëüíîãî íåð³âíîì³ðíîãî ðóõó ñåðåäíÿ øâèäê³ñòü âè-
çíà÷àºòüñÿ çà ôîðìóëîþ
υ=
r
r
c
s
t
.
Ìàë. 46. гâíîïðèñêîðåíèé ðóõ ò³ë,
ùî ðóõàþòüñÿ íàçóñòð³÷ îäèí îäíîìó
Ìàë. 47. Ãðàô³ê ïðîåêö³¿ øâèäêîñò³
ð³âíîïðèñêîðåíîãî ðóõó

53
ʳíåìàòèêà ïîñòóïàëüíîãî òà îáåðòàëüíîãî ðóõ³â ìàòåð³àëüíî¿ òî÷êè
Ìîæíà ïåðåêîíàòèñü ó òîìó, ùî ïåðåì³ùåííÿ ïðè ð³âíîïðèñêîðåíîìó ðóñ³
âèðàæàºòüñÿ ïëîùåþ òðàïåö³¿ ÎÀÂÑ (ìàë. 47). Ç êóðñó ãåîìåò𳿠â³äîìî, ùî
ïëîùà òðàïåö³¿ äîð³âíþº äîáóòêó ï³âñóìè îñíîâ íà âèñîòó. Ó íàøîìó âèïàäêó
äîâæèíà îäí³º¿ îñíîâè
υ
0x
, ³íøî¿
υ
x
, âèñîòà òðàïåö³¿ – t . ϳâñóìà îñíîâ – öå
ñåðåäíÿ ë³í³ÿ òðàïåö³¿, òîáòî, ÿê ìè äîâåëè, ñåðåäíÿ øâèäê³ñòü ð³âíîïðèñêîðå-
íîãî ðóõó.
ʳíåìàòè÷íå ð³âíÿííÿ ïåðåì³ùåííÿ ïðè ð³âíîïðèñêîðåíîìó ðóñ³ â ïðîåê-
ö³ÿõ íà âèáðàíó â³ñü:
=υ +
2
0
2
x
xx
at
st
.
ßêùî ïî÷àòêîâà øâèäê³ñòü äîð³âíþº íóëþ, òî υ
0õ
= 0, òî s
x
= a
x
t
2
/2.
Äëÿ ïðÿìîë³í³éíîãî ðóõó ïðîåêö³ÿ âåêòîðà ïåðåì³ùåííÿ âèçíà÷àºòüñÿ ÿê
=−
0x
sxx, òîä³
=+υ+
2
0
2
x
ox
at
xx t
.
Ìîæíà âèâåñòè é ³íøó ôîðìóëó äëÿ ïåðåì³ùåííÿ.
²ç
υ=υ +
xoxx
at âèðàçèìî ÷àñ
υ−υ
=
0xx
x
t
a
³ ï³äñòàâèìî éîãî ó ê³íåìàòè÷íå
ð³âíÿííÿ ïåðåì³ùåííÿ
⎛⎞
υ−υ υ−υ
=υ +
⎜⎟
⎝⎠
2
00
0
2
xxxxx
xx
xx
a
s
aa
.
ϳñëÿ ñïðîùåíü:
υ−υ
=
22
0
2
xx
x
x
s
a
, àáî
υ−υ =
22
0
2
xx xx
as.
Ö³ ôîðìóëè äàþòü çìîãó çíàéòè ïåðåì³ùåííÿ ò³ëà, ÿêùî â³äîìèìè º ïðè-
ñêîðåííÿ, ïî÷àòêîâà ³ ê³íöåâà øâèäêîñò³ ðóõó ò³ëà.
Ó âåêòîðí³é ôîðì³ ê³íåìàòè÷í³ ð³âíÿííÿ ð³âíîïðèñêîðåíîãî ðóõó ìàþòü
âèãëÿä:
=υ +
2
0
2
at
st
rr
r
;
22
0
2.asυ−υ=
rr
rr
Дайте відповіді на запитання
Çà áóäü-ÿêîãî íåð³âíîì³ðíîãî ðóõó çì³íþºòüñÿ øâèäê³ñòü. ßê ïðèñêî-1.
ðåííÿ õàðàêòåðèçóº öþ çì³íó?
ßê ñïðÿìîâàíî âåêòîð ïðèñêîðåííÿ ïðè ïðÿìîë³í³éíîìó ð³âíîïðèñêî-2.
ðåíîìó ðóñ³?  ÿêîìó âèïàäêó ïðîåêö³ÿ ïðèñêîðåííÿ ìຠäîäàòíå, à â ÿêîìó
â³ä’ºìíå çíà÷åííÿ?
3. Øâèäê³ñòü ïðÿìîë³í³éíîãî ðóõó ò³ëà ùîñåêóíäè çá³ëüøóºòüñÿ íà 2 %:
à) â³ä ïî÷àòêîâîãî çíà÷åííÿ; á) â³ä çíà÷åííÿ øâèäêîñò³ íà ïî÷àòêó êîæíî¿ ñå-
êóíäè. ×è ñòàëå ïðèñêîðåííÿ ò³ëà â îáîõ âèïàäêàõ?

54
Ð Î Ç Ä ² Ë 1
4. Ò³ëî ïî÷èíຠðóõàòèñü ³ç ñòàíó ñïîêîþ ïðÿìîë³í³éíî, ïðîõîäÿ÷è ùîñå-
êóíäè øëÿõ, íà 1 ì á³ëüøèé, í³æ çà ïîïåðåäíþ ñåêóíäó. ×è ñòàëå ïðèñêîðåííÿ
ò³ëà?
5. ×è ìîæóòü äâà ò³ëà, ÿê³ ðóõàþòüñÿ ïî îäí³é ïðÿì³é â ïðîòèëåæíèõ íà-
ïðÿìàõ, ìàòè îäíàêîâ³ âåêòîðè ïðèñêîðåíü?
Приклад розв’язування задач
Óðàõîâóþ÷è, ùî âñ³ òðè âåêòîðè
υ
r
,
υ
r
0
,
r
a
ñïðÿìîâàí³ âçäîâæ îäí³º¿ ïðÿìî¿,
òî ìîäóë³ ¿õ ïðîåêö³é äîð³âíþþòü ìîäóëþ ñàìèõ âåêòîð³â, à çíàêè ïðîåêö³é
âèçíà÷àþòüñÿ òèì, ÿê íàïðàâëåí³ âåêòîðè â³äíîñíî âèáðàíî¿ êîîðäèíàò-
íî¿ îñ³. ßêùî çíàêè ïðîåêö³é âåêòîð³â
υ
r
0
³
r
a
ñï³âïàäàþòü, òî ìîäóëü øâèäêîñò³
υ çðîñòຠç ÷àñîì – ò³ëî ðîçãàíÿºòüñÿ ³ âñ³ âåêòîðè
υ
r
,
υ
r
0
,
r
a
íàïðàâëåí³ â îäèí
á³ê. ßêùî
υ
r
0
³
r
a
ïðîòèëåæí³, òî ò³ëî – ãàëüìóº, ³ âåêòîð
r
a
íàïðàâëåíèé ïðî-
òèëåæíî äî âåêòîð³â
υυ
rr
0
, .
Çàäà÷à. гâíÿííÿ ðóõó ò³ëà çàäàíî ó âèãëÿä³
=+
2
15 0,4xt t
, äå âñ³ âåëè÷èíè
çàäàíî â Ѳ. Âèçíà÷èòè ïî÷àòêîâó øâèäê³ñòü ³ ïðèñêîðåííÿ ðóõó ò³ëà, à òàêîæ
êîîðäèíàòó ³ øâèäê³ñòü ðóõó ò³ëà ÷åðåç 5 ñ.
Äàíî:
=+
2
15 0,4xt t
;
= 5ct
Ðîçâ’ÿçàííÿ:
Ïîð³âíÿºìî öå ð³âíÿííÿ ðóõó
=+
2
15 0,4xt t
³ç çàãàëüíèì:
=+υ+
2
0
2
x
ox
at
xx t
.
Î÷åâèäíî, ùî x
0
= 0, êîåô³ö³ºíò ïðè t äîð³âíþº υ
0
= 15 ì/ñ,
à ïðè t
2
â³äïîâ³äíî a/2 = 0,4, çâ³äêè a = 0,8 ì/ñ
2
.
υ−
0
?
−?a
−?x
υ−?
Êîîðäèíàòó ÷åðåç 5 ñ âèçíà÷èìî ç ð³âíÿííÿ ïðè t = 5 c:
2
22
ì
0,8
ì
ñ
15 5 c 5 c 85 ì
ñ2
x =⋅+ ⋅=
.
Øâèäê³ñòü ðóõó ò³ëà âèçíà÷èìî çà ôîðìóëîþ υ = υ
0
+ at ïðè t = 5 c:
2
ìì
15 0,8 5 ñ 19 ì ñ
ññ
υ= + ⋅ =
.
Âèçíà÷èòè çíà÷åííÿ øâèäêîñò³ ³ ïðèñêîðåííÿ ìîæíà, ñêîðèñòàâøèñü òà-
êîæ âèçíà÷åííÿì ïîõ³äíî¿.
υ= = + = +
′′
2
(15 0,4 ) 15 0,8xtt t
, ïðè t = 5 c:
2
ìì
15 0,8 5 ñ 19 ì ñ
ññ
υ= + ⋅ =
.
=υ = + =
′′
2
(15 0,8 ) 0,8ì ñat.
³äïîâ³äü: υ=
0
15ì ñ ; =
2
0,8 ì ña ; = 85ìx ; υ=19ì ñ .

55
ʳíåìàòèêà ïîñòóïàëüíîãî òà îáåðòàëüíîãî ðóõ³â ìàòåð³àëüíî¿ òî÷êè
Вправа 6
1. Ðóõ ìàòåð³àëüíî¿ òî÷êè çàäàíî ð³âíÿííÿìè: x = 8t
2
+ 4; y = 6t
2
− 3; z = 0.
Âñ³ âåëè÷èíè çàïèñàíî â Ѳ. Âèçíà÷èòè ìîäóë³ øâèäêîñò³ òà ïðèñêîðåííÿ ó ìî-
ìåíò ÷àñó t = 10 c.
2. ßêèé øëÿõ ïðîéäå ò³ëî çà ÷àñ t = 10 c â³ä ïî÷àòêó ðóõó, ÿêùî ð³âíÿííÿ
éîãî ðóõó x = 2t
2
+ 3t + 4, y = 3t
2
+ 4t − 2, z = 0? (Âñ³ âåëè÷èíè çàïèñàíî â Ѳ).
3. Ïî ñõèëó çàâäîâæêè 100 ì ëèæíèê ç’¿õàâ çà 20 ñ, ðóõàþ÷èñü ³ç ïðèñêî-
ðåííÿì 0,3 ì/ñ
2
. ßêó øâèäê³ñòü ìàâ ëèæíèê íà ïî÷àòêó ³ â ê³íö³ ñõèëó?
4. Êóëüêà, ùî êîòèòüñÿ ïîõèëèì æîëîáîì ç³ ñòàíó ñïîêîþ, çà ïåðøó ñåêóí-
äó ïðîéøëà 10 ñì. ßêèé øëÿõ êóëüêà ïðîéäå çà òðè ñåêóíäè?
5. Ó ñê³ëüêè ðàç³â øâèäê³ñòü ðóõó êóë³ óñåðåäèí³ ñòâîëà ðóøíèö³ ìåíøà,
í³æ ï³ä ÷àñ ïîñòð³ëó?
6. Ò³ëî, ðóõàþ÷èñü ð³âíîïðèñêîðåíî, ïðîòÿãîì ÷åòâåðòî¿ ñåêóíäè ïðîéøëî
35 ì. Ç ÿêèì ïðèñêîðåííÿì ðóõàëîñü ò³ëî? ßêà éîãî øâèäê³ñòü íàïðèê³íö³ ÷åòâåð-
òî¿, à òàêîæ äåñÿòî¿ ñåêóíäè ðóõó? ßêèé øëÿõ ïðîéøëî ò³ëî çà äðóãó, à òàêîæ çà
ï’ÿòó ñåêóíäó? ßêèé øëÿõ ïðîéøëî ò³ëî çà äðóãó ³ òðåòþ ñåêóíäè, ðàçîì óçÿò³?
7. Çà ÷àñ t = 10 c ò³ëî ïðîéøëî s = 18 ì, ïðè öüîìó éîãî øâèäê³ñòü çá³ëüøèëàñü
ó n = 5 ðàç³â. Ââàæàþ÷è ðóõ ð³âíîïðèñêîðåíèì, âèçíà÷èòè ïðèñêîðåííÿ ò³ëà.
8. Ò³ëî, ÿêå ðóõàëîñü ð³âíîì³ðíî ç øâèäê³ñòþ 2 ì/ñ, ç äåÿêî¿ òî÷êè À ïî÷è-
íຠðóõàòèñü ç ïðèñêîðåííÿì 0,5 ì/ñ
2
. ×åðåç 30 ñ ³ç ö³º¿ ñàìî¿ òî÷êè ñë³äîì çà
ïåðøèì ò³ëîì ïî÷èíຠðóõàòèñü ³ç ïî÷àòêîâîþ øâèäê³ñòþ 5 ì/ñ ³ ïðèñêîðåííÿì
2 ì/ñ
2
äðóãå ò³ëî. ×åðåç ñê³ëüêè ÷àñó äðóãå ò³ëî íàçäîæåíå ïåðøå?
9. Ò³ëî ïî÷èíຠðóõ ç òî÷êè À ³ ðóõàºòüñÿ ñïåðøó ð³âíîïðèñêîðåíî ïðîòÿ-
ãîì ÷àñó t
0
, à ïîò³ì ç òèì ñàìèì çà ìîäóëåì ïðèñêîðåííÿì – ñïîâ³ëüíåíî. ×åðåç
ÿêèé ÷àñ â³ä ïî÷àòêó ðóõó ò³ëî ïîâåðíåòüñÿ ó òî÷êó À?
10. Äîâåä³òü, ùî ï³ä ÷àñ ïðÿìîë³í³éíîãî ð³âíîïðèñêîðåíîãî ðóõó áåç ïî-
÷àòêîâî¿ øâèäêîñò³ ñïðàâäæóºòüñÿ ð³âí³ñòü s
1
: s
2
: ... s
n
= 1 : 3 : ...(2n − 1) – â³ä-
ñòàí³, ÿê³ ïðîõîäèòü ò³ëî çà ïîñë³äîâí³ îäíàêîâ³ ³íòåðâàëè ÷àñó, â³äíîñÿòüñÿ ÿê
ïîñë³äîâí³ íåïàðí³ ÷èñëà.
§ 11 Графічне зображення рівноприскореного руху
Ãðàô³ê ïðîåêö³¿ ïðèñêîðåííÿ 3 a
x
= a
x
(t).
Ãðàô³ê ïðîåêö³¿ øâèäêîñò³
3 υ
x
= υ
x
(t).
Ãðàô³ê ïðîåêö³¿ ïåðåì³ùåííÿ s
3
x
= s
x
(t) ³ êîîðäèíàòè x = x (t).
Ãðàô³ê ïðîåêö³¿ ïðèñêîðåííÿ a
x
= a
x
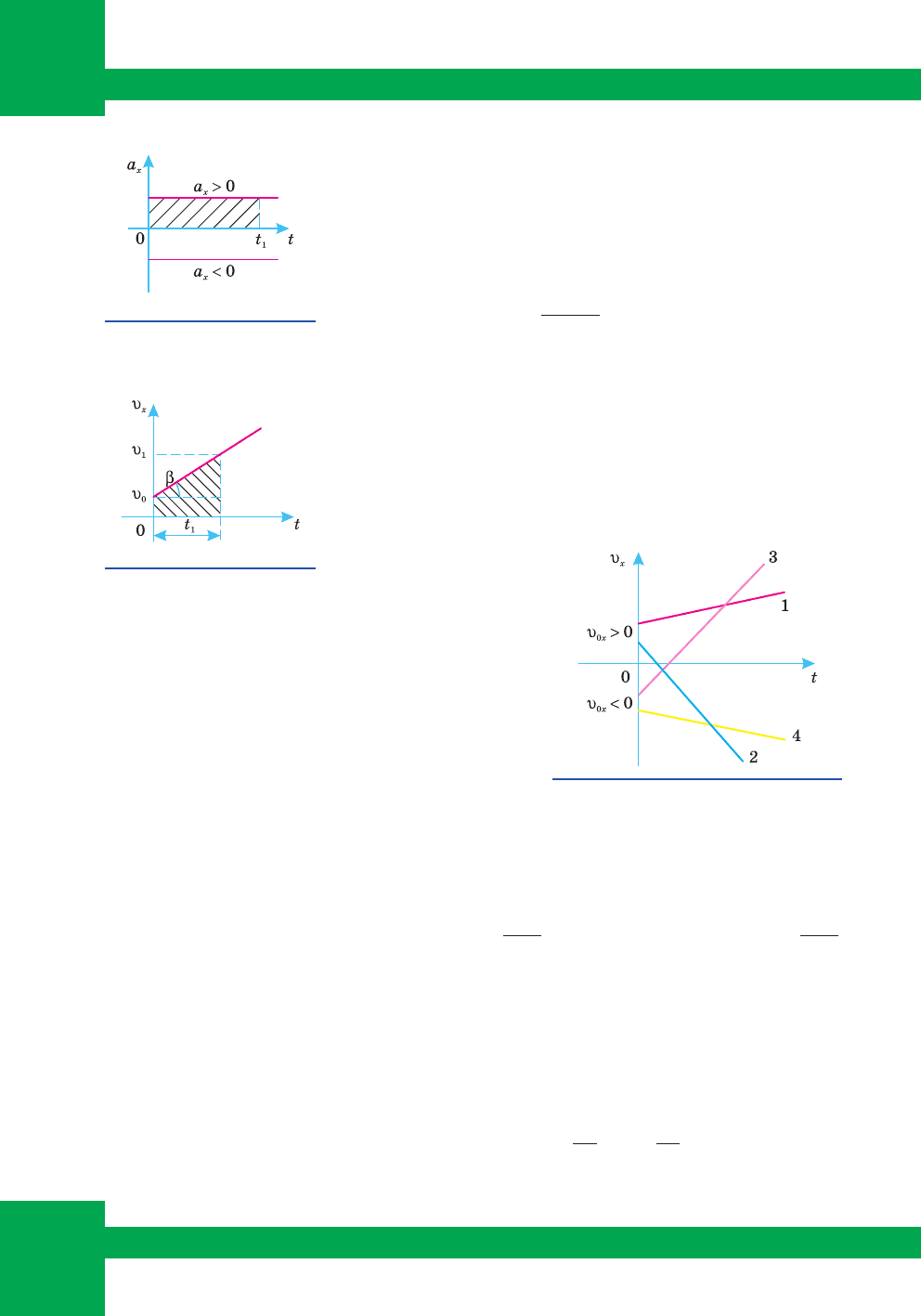
(t). Îñê³ëüêè ï³ä ÷àñ ð³âíîïðèñêîðå-
íîãî ðóõó ïðèñêîðåííÿ º âåëè÷èíîþ ñòàëîþ, òî ãðàô³êîì çàëåæíîñò³ ïðîåêö³¿
ïðèñêîðåííÿ â³ä ÷àñó º ïðÿìà, ïàðàëåëüíà îñ³ ÷àñó (ìàë. 48).
Çà ïëîùåþ ô³ãóðè, îáìåæåíî¿ ãðàô³êîì òà ïåðïåíäèêóëÿðîì, îïóùåíèì
íà â³ñü ÷àñó, ìîæíà âèçíà÷èòè øâèäê³ñòü ðóõó ò³ëà ó ïåâíèé ìîìåíò ÷àñó t
1
.
56
Ð Î Ç Ä ² Ë 1
Ãðàô³ê ïðîåêö³¿ øâèäêîñò³ υ
x
= υ
x
(t). ßê âèäíî ç ð³â-
íÿííÿ
υ=υ +
xoxx
at, çàëåæí³ñòü ïðîåêö³¿ øâèäêîñò³ â³ä
÷àñó ë³í³éíà, òîìó ãðàô³êîì º ïðÿìà (ìàë. 49) (ïîð³âíÿé-
òå ç â³äîìèì âàì ãðàô³êîì ôóíêö³¿ y = ax + b,
§4).
Êóò íàõèëó ãðàô³êó çàëåæíîñò³ ïðîåêö³¿ øâèäêî-
ñò³ â³ä ÷àñó âèçíà÷àºòüñÿ ÷èñëîâèì çíà÷åííÿì ïðèñêî-
ðåííÿ, ÿêå ãðàô³÷íî ìîæíà âèçíà÷èòè òàê:
10
1
tga
t
υ−υ
==β
.
Çà ïëîùåþ ô³ãóðè îáìåæåíî¿ ãðàô³êîì øâèäêîñò³
òà ïåðïåíäèêóëÿðîì, îïóùåíèì íà â³ñü ÷àñó ìîæíà âè ç-
íà÷èòè äîâæèíó ïðî éäåíîãî øëÿõó íà äàíèé ìîìåíò ÷àñó
t
1
. Òàêîæ çà öèì ãðàô³êîì ìîæíà çàïèñàòè çàêîí ðóõó.
Çàëåæíî â³ä ïðîåêö³¿ ïðèñêîðåííÿ ³ ïî÷àòêîâî¿
øâèäêîñò³ ðóõó ò³ëà ãðàô³ê ìàòèìå ð³çíèé âèãëÿä.
Òàê, äëÿ çîáðàæåíèõ íà ìàë. 50 ãðàô³êàõ âèêîíóþòüñÿ
òàê³ óìîâè:
1) υ
x0
> 0, a
x
> 0;
2) υ
x0
> 0, a
x
< 0;
3) υ
x0
< 0, a
x
> 0;
4) υ
x0
< 0, a
x
< 0.
ßêùî υ
x0
= 0, òî ïðÿìà âèõîäèòèìå ç ïî-
÷àòêó êîîðäèíàò ³, çàëåæíî â³ä çíà÷åííÿ ïðî-
åêö³¿ ïðèñêîðåííÿ, áóäå íàïðàâëåíà âãîðó àáî
âíèç. Íàïðÿì ïðÿìèõ çàëåæèòü â³ä çíà÷åííÿ
ïðèñêîðåííÿ: ÷èì á³ëüøå éîãî çíà÷åííÿ, òèì
êðóò³øå çä³éìàºòüñÿ ÷è ñïàäຠãðàô³ê. Çâåð-
í³òü óâàãó íà òå, ùî ãðàô³êè 2 ³ 3 ïåðåòèíàþòü
â³ñü ÷àñó. Öå îçíà÷àº, ùî ó äåÿêèé ìîìåíò
÷àñó ¿õ øâèäê³ñòü äîð³âíþâàëà íóëþ (ò³ëî çó-
ïèíÿëîñü) ³ ïðîäîâæóâàëî ðóõ ó çâîðîòíîìó
íàïðÿì³.
Ãðàô³ê ïðîåêö³¿ ïåðåì³ùåííÿ s
x
= s
x
(t) ³ êîîðäèíàòè x = x (t). ʳíåìàòè÷í³
ð³âíÿííÿ ïðîåêö³¿ ïåðåì³ùåííÿ
=υ +
2
0
2
x
xx
at
st
³ êîîðäèíàòè =+υ+
2
0
2
x
ox
at
xx t
º êâàäðàòíèìè ð³âíÿííÿìè âèãëÿäó y = c + bx + ax
2
, òîìó ãðàô³êàìè çàëåæ-
íîñò³ ïðîåêö³¿ ïåðåì³ùåííÿ ³ êîîðäèíàòè â³ä ÷àñó º ïàðàáîëè (äèâ. §4).
óëêè öèõ ïàðàáîë çã³äíî ç ïàðàìåòðàìè ðóõó ìàþòü ð³çíèé âèãëÿä.
ßêùî υ
0x
= 0 ³ a
x
> 0, òî ãðàô³êè ìàþòü âèãëÿä, ÿê íà ìàë. 51.
ßêùî υ
0x
= 0 ³ a
x
< 0, òî ã³ëêè ïàðàáîëè çîð³ºíòîâàí³ âíèç (ìàë. 52).
ßêùî
υ≠
0
0
x
³ ≠
0
0x , òî âåðøèíà ïàðàáîëè çì³ùóºòüñÿ â òî÷êó, êîîðäèíà-
òè ÿêî¿ âèçíà÷àþòüñÿ ñï³ââ³äíîøåííÿìè:
υ
=−
2
0
0
2
xx
a
,
υ
=−
0
t
a
(ìàë. 53).
Ìàë. 48. Ãðàô³ê
ïðîåêö³¿ ïðèñêîðåííÿ
Ìàë. 49. Ãðàô³ê
ïðîåêö³¿ øâèäêîñò³
Ìàë. 50. Âèãëÿä ãðàô³êà υ
x
= υ
x
(t)
ïðè â³äïîâ³äíèõ çíà÷åííÿõ
υ
x0
³ a
x
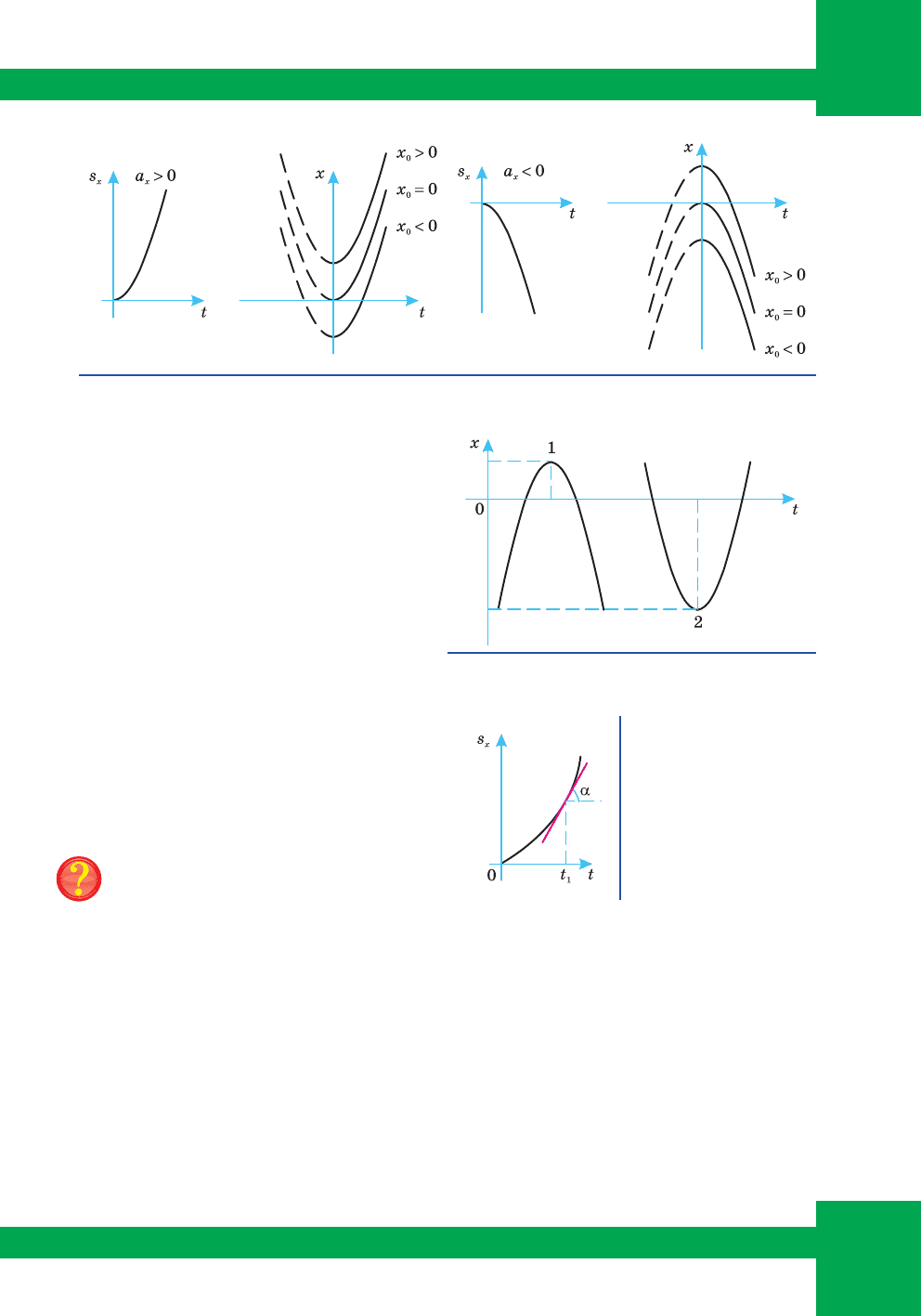
57
ʳíåìàòèêà ïîñòóïàëüíîãî òà îáåðòàëüíîãî ðóõ³â ìàòåð³àëüíî¿ òî÷êè
Çà ô³çè÷íèì çì³ñòîì øâèäê³ñòü
º ïîõ³äíîþ â³ä ïåðåì³ùåííÿ, âîä-
íî÷àñ çà ãåîìåòðè÷íèì çì³ñòîì ïî-
õ³äíà âèçíà÷àºòüñÿ êóòîì íàõèëó
äîòè÷íî¿ äî êðèâî¿, òîìó øâèäê³ñòü
ðóõó ò³ëà ó ïåâíèé ìîìåíò ÷àñó t
1
âèçíà÷àºòüñÿ òàíãåíñîì êóòà íà-
õèëó äîòè÷íî¿ äî ãðàô³êà ïðîåêö³¿
ïåðåì³ùåííÿ ³ â³ññþ ÷àñó (ìàë. 54)
υ = tgα.
Çà çì³íîþ êóòà íàõèëó äîòè÷íèõ
äî ãðàô³êà ìîæíà ïðîñë³äêóâàòè çà
çì³íîþ øâèäêîñò³ ðóõó ò³ëà.
Îñîáëèâîñò³ ïîáóäîâè ãðàô³êà øëÿ-
õó ð³âíîïðèñêîðåíîãî ðóõó l = l(t)
ïîëÿ-
ãàþòü ó òîìó, ùî â³í ðîçòàøîâàíèé âè-
êëþ÷íî íàä â³ññþ ÷àñó, îñê³ëüêè øëÿõ
íå ìîæå íàáóâàòè â³ä’ºìíèõ çíà÷åíü.
Дайте відповіді на запитання
Ó ÿêèõ âèïàäêàõ ãðàô³ê ïðî-1.
åêö³¿ øâèäêîñò³ ð³âíîïðèñêîðåíîãî ðóõó íàïðÿìëåíèé âãîðó, à â ÿêèõ – âíèç?
Ùî îçíà÷ຠïåðåòèí ãðàô³êîì ïðîåêö³¿ øâèäêîñò³ îñ³ ÷àñó?
ßêó ôîðìó ìຠãðàô³ê ïðîåêö³¿ ïåðåì³ùåííÿ? ×èì â³äð³çíÿþòüñÿ ãðà-2.
ô³êè ïðîåêö³¿ ïåðåì³ùåííÿ ³ êîîðäèíàòè?
Ðîçêàæ³òü, ÿê çà ãðàô³êàìè ïðèñêîðåííÿ, øâèäêîñò³ òà ïåðåì³ùåííÿ 3.
âèçíà÷èòè:
à) øâèäêîñò³ äëÿ áóäü-ÿêîãî ìîìåíòó ÷àñó çà ãðàô³êîì ïðèñêîðåííÿ;
á) çàêîí ðóõó çà ãðàô³êîì øâèäêîñò³;
â) çì³íó øâèäêîñò³ çà ãðàô³êîì ïåðåì³ùåííÿ;
ã) ïðèñêîðåííÿ çà ãðàô³êîì øâèäêîñò³.
Ìàë. 51. Ãðàô³ê ïðîåêö³¿ ïåðåì³ùåííÿ
³ êîîðäèíàòè ïðè υ
0x
= 0 ³ a
x
> 0
Ìàë. 52. Ãðàô³ê ïðîåêö³¿ ïåðåì³ùåííÿ
³ êîîðäèíàòè ïðè υ
0x
= 0 ³ a
x
> 0
Ìàë. 53. Ãðàô³ê ðóõó ïðè:
1. υ
0x
> 0, a
x
< 0; 2. υ
0x
< 0, a
x
> 0
Ìàë. 54.
Çà òàíãåíñîì êóòà
íàõèëó äîòè÷íî¿ äî
ãðàô³êà ïðîåêö³¿
ïåðåì³ùåííÿ ìîæíà
âèçíà÷èòè øâèäê³ñòü
ó ïåâíèé ìîìåíò
÷àñó
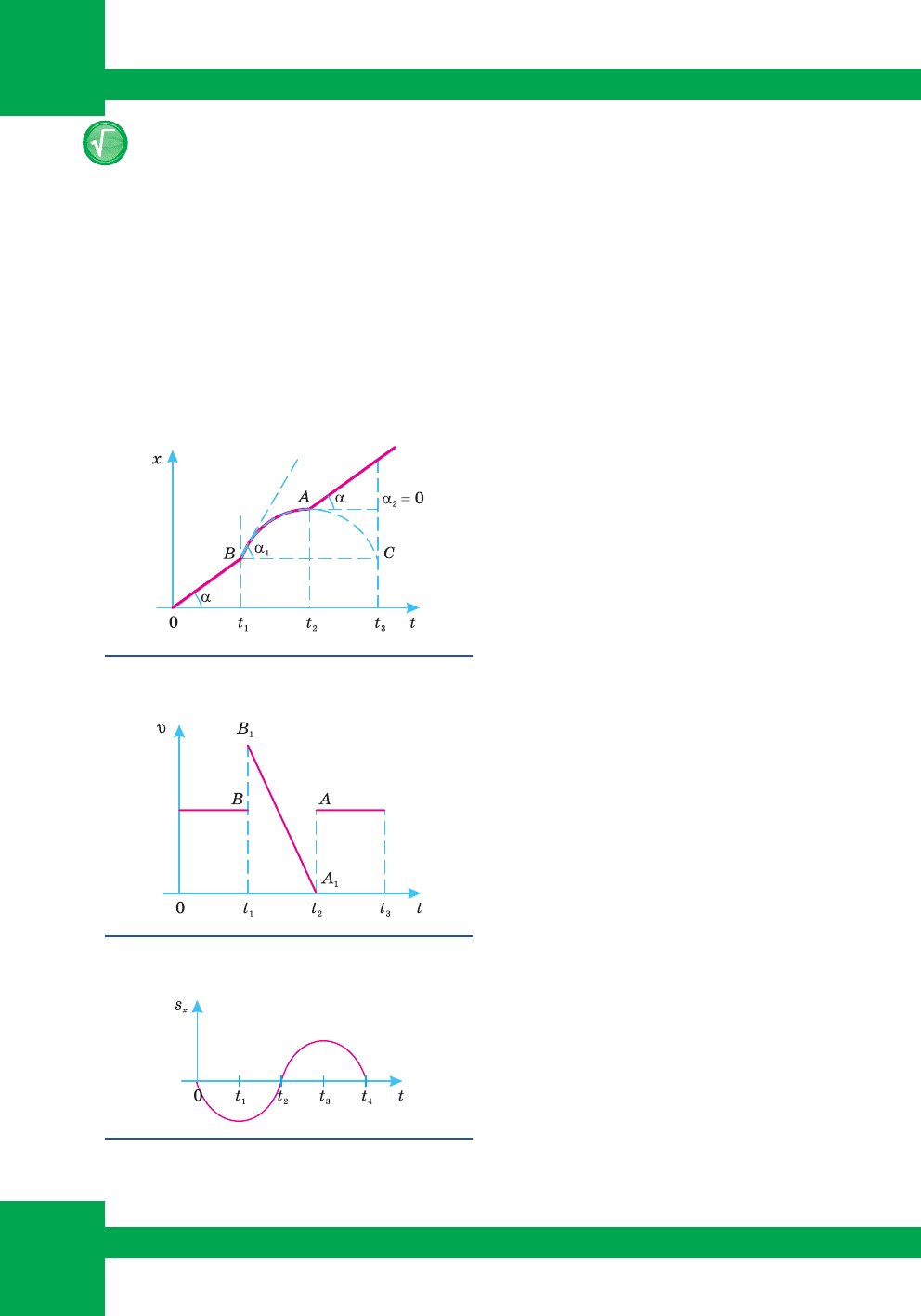
58
Ð Î Ç Ä ² Ë 1
Приклади розв’язування задач
Çàäà÷à 1. Çà ãðàô³êîì, ùî ìຠçëàìè (ìàë. 55), íàêðåñëèòè ãðàô³ê çàëåæ-
íîñò³ øâèäêîñò³ ðóõó ò³ëà â³ä ÷àñó òà îõàðàêòåðèçóâàòè éîãî.
Ðîçâ’ÿçàííÿ:
Ðîçãëÿíåìî ãðàô³ê çàëåæíîñò³ êîîðäèíàòè â³ä ÷àñó: ïðîòÿãîì ÷àñó t
1
ò³ëî ðóõà-
ëîñÿ ð³âíîì³ðíî ³ ïðÿìîë³í³éíî (tgα = υ).
Ïðîòÿãîì ÷àñó â³ä t
1
äî t
2
– ð³âíîñïîâ³ëüíåíî, ïðè÷îìó, îñê³ëüêè â òî÷êàõ
 ³ À ñïî ñòåð³ãàþòüñÿ çëàìè, òî öå îçíà÷àº, ùî øâèäê³ñòü ðóõó ò³ëà ð³çêî çì³íè-
ëàñÿ: ó òî÷ö³  â³ä υ = tgα äî υ
1
= tgα
1
, ó òî÷ö³ À â³ä υ
2
= 0, îñê³ëüêè α
2
= 0 äî υ =
tgα.
Ïðîòÿãîì ÷àñó â³ä t
2
äî t
3
ò³ëî ðóõàëîñü ð³âíîì³ðíî ç òàêîþ ñàìîþ øâèäê³ñ-
òþ, ùî áóëà ³ íà ïî÷àòêó ðóõó.
Îñê³ëüêè ãðàô³ê çàëåæíîñò³ êîîð-
äèíàòè â³ä ÷àñó ìຠçëàìè, òî ãðàô³ê
çàëåæíîñò³ øâèäêîñò³ ðóõó â³ä ÷àñó
ìàòèìå ðîçðèâè ó ìîìåíòè ÷àñó t
1
òà
t
2
(ìàë. 56).
Çàäà÷à 2. Çà ãðàô³êîì ïðîåêö³¿ ïå-
ðåì³ùåííÿ (ìàë. 57) ïîáóäóâàòè ãðà-
ô³ê øâèäêîñò³ òà ïðèñêîðåííÿ.
Ðîçâ’ÿçàííÿ:
Çà ãðàô³êîì çàëåæíîñò³ ïðîåêö³¿
ïåðåì³ùåííÿ â³ä ÷àñó ïðîàíàë³çóºìî
õàðàêòåð ðóõó ò³ëà.
Íà ïî÷àòêó ðóõó äî ìîìåíòó t
1
ò³-
ëî ðóõàºòüñÿ ó íàïðÿì³ ïðîòèëåæíî-
ìó äî â³ñ³ Õ, ïðîåêö³ÿ øâèäêîñò³ ðóõó
â³ä’ºìíà.
Ç ìîìåíòó ÷àñó t
1
ò³ëî çì³íþº íà-
ïðÿì ðóõó ³ äî ìîìåíòó t
2
ðóõàºòüñÿ
ó íàïðÿì³ îñ³ Õ. Ïðîåêö³ÿ øâèäêîñò³
ïðè öüîìó äîäàòíà.
Îñê³ëüêè íà ³íòåðâàë³ â³ä 0 äî t
2
ã³ëêè ïàðàáîëè ñïðÿìîâàí³ âãîðó, òî
ïðîòÿãîì öüîãî ïåð³îäó ïðèñêîðåííÿ
ò³ëà çàëèøàºòüñÿ äîäàòíèì.
Äî ìîìåíòó ÷àñó t
3
ò³ëî ïðîäîâæóº
ðóõàòèñü ó òîìó ñàìîìó íàïðÿì³, ïðî-
åêö³ÿ øâèäêîñò³ äîäàòíà, àëå çìåíøó-
ºòüñÿ çà ìîäóëåì, òîìó ïðèñêîðåííÿ –
â³ä’ºìíå.
Ç ìîìåíòó t
3
ò³ëî çì³íþº íàïðÿì
ðóõó ³ äî ìîìåíòó t
4
çíîâó ðóõàºòüñÿ
ó íàïðÿì³, ïðîòèëåæíîìó â³ñ³ Õ, òîìó
ïðîåêö³ÿ øâèäêîñò³ â³ä’ºìíà ³ çðîñòàº
Ìàë. 56.
Ãðàô³ê çàëåæíîñò³ øâèäêîñò³ â³ä ÷àñó
Ìàë. 57.
Ãðàô³ê ïðîåêö³¿ ïåðåì³ùåííÿ
Ìàë. 55.
Ãðàô³ê ðóõó ò³ëà
59
ʳíåìàòèêà ïîñòóïàëüíîãî òà îáåðòàëüíîãî ðóõ³â ìàòåð³àëüíî¿ òî÷êè
çà ìîäóëåì, îñê³ëüêè ïðîòÿãîì óñüîãî ³íòåðâà-
ëó â³ä t
3
äî t
4
ïðèñêîðåííÿ â³ä’ºìíå (ã³ëêè ïà-
ðàáîëè íàïðàâëåí³ âíèç).
Ãðàô³êè ïðîåêö³¿ øâèäêîñò³ òà ïðîåêö³¿
ïðèñêîðåííÿ óêàçàíî íà ìàë. 58.
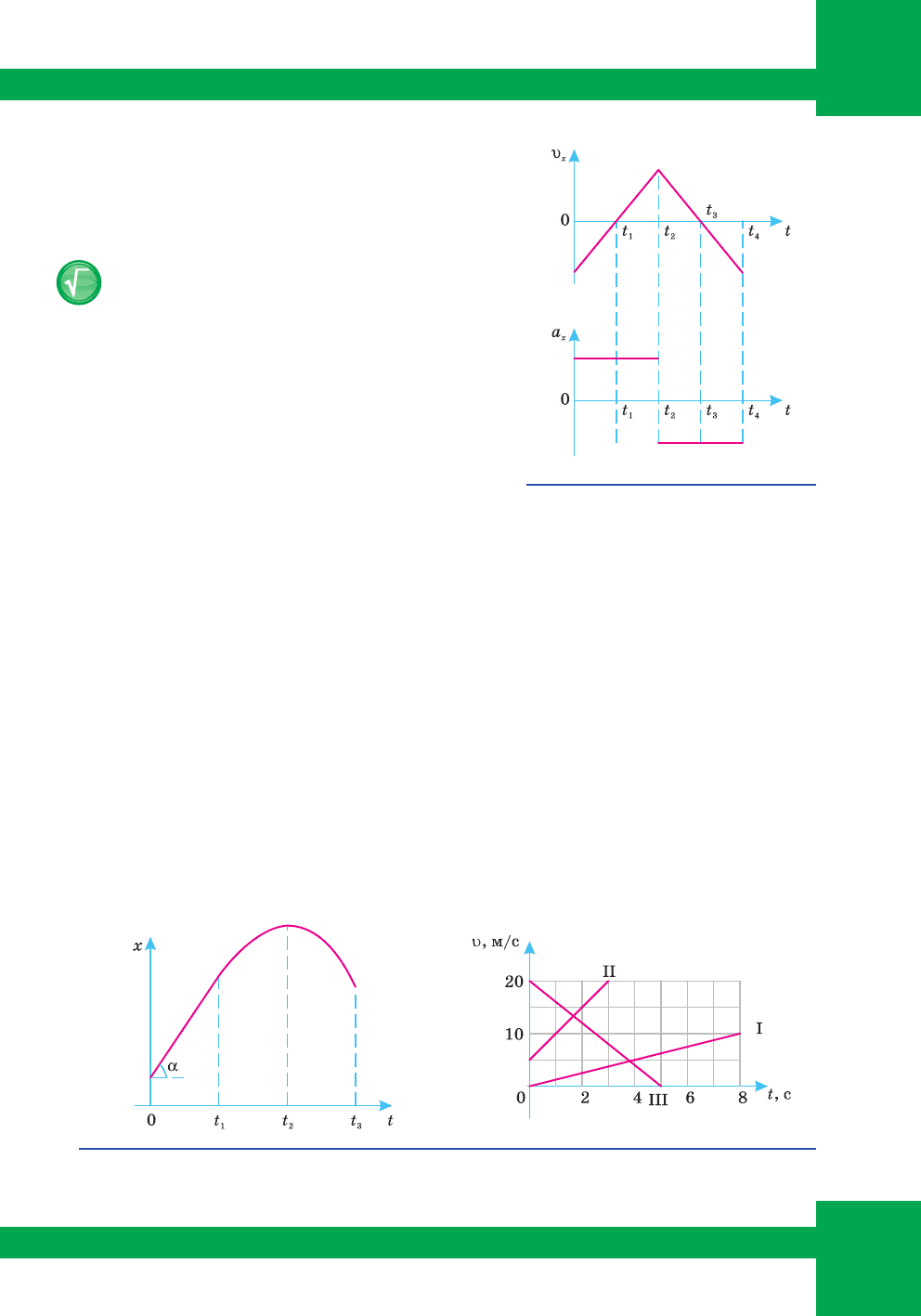
Вправа 7
1. Ðóõè ìàòåð³àëüíèõ òî÷îê çàäà-
íî òàêèìè ð³âíÿííÿìè: à)
=+
2
1
10 0,4xtt;
á)
=−
2
2
2xtt; â) =− +
2
3
42xtt; ã) =− −
2
4
6xtt.
Âñ³ âåëè÷èíè çàïèñàíî â Ѳ. Íàïèñàòè çàëåæ-
í³ñòü υ = υ(t) äëÿ êîæíîãî âèïàäêó; ïîáóäóâàòè
ãðàô³êè öèõ çàëåæíîñòåé; âèçíà÷èòè âèä ðóõó
ó êîæíîìó âèïàäêó.
2. Õëîï÷èê ç’¿õàâ íà ñàí÷àòàõ ç ãîðè, ùî
ìຠñõèë 40 ì, çà 10 ñ, à ïîò³ì ïðî¿õàâ ïî ãî-
ðèçîíòàëüí³é ä³ëÿíö³ ùå 20 ì ³ çóïèíèâñÿ.
Îá÷èñëèòè øâèäê³ñòü ó ê³íö³ ñõèëó, ïðèñêî-
ðåííÿ íà êîæí³é ä³ëÿíö³, çàãàëüíèé ÷àñ ðóõó ³ ñåðåäíþ øâèäê³ñòü íà âñüîìó
øëÿõó. Íàêðåñëèòè ãðàô³ê øâèäêîñò³.
3. Âåëîñèïåäèñò ïåðø³ 4 ñ ðóõàâñÿ ç³ ñòàíó ñïîêîþ ç ïðèñêîðåííÿì 1 ì/ñ
2
, à
ïîò³ì 0,1 õâ ¿õàâ ð³âíîì³ðíî, à îñòàíí³ 20 ì, ïîêè íå çóïèíèâñÿ, ð³âíîñïîâ³ëü-
íåíî. Îá÷èñëèòè ñåðåäíþ øâèäê³ñòü çà âåñü ÷àñ ðóõó. Ïîáóäóâàòè ãðàô³ê υ
õ
(t).
4. Íà ìàë. 59 ïîäàíî ãðàô³ê çàëåæíîñò³ êîîðäèíàòè ò³ëà â³ä ÷àñó. ϳñëÿ
ìîìåíòó ÷àñó t
1
êðèâà ãðàô³êà – ïàðàáîëà. ßêèé ðóõ çîáðàæåíî íà öüîìó ãðà-
ô³êó? Ïîáóäóâàòè ãðàô³ê çàëåæíîñò³ øâèäêîñò³ ò³ëà â³ä ÷àñó.
5. Çà íàâåäåíèìè íà ìàë. 60 ãðàô³êàìè íàïèñàòè ð³âíÿííÿ çàëåæíîñò³ υ
x
(t) ³
ð³âíÿííÿ õ = õ(t). Ââàæàòè, ùî ó ïî÷àòêîâèé ìîìåíò (t = 0) ò³ëî ïåðåáóâຠó ïî÷àò-
êó êîîðäèíàò (x = 0). Ïîáóäóâàòè ãðàô³êè çàëåæíîñò³ õ = õ(t) äëÿ êîæíîãî ç ò³ë.
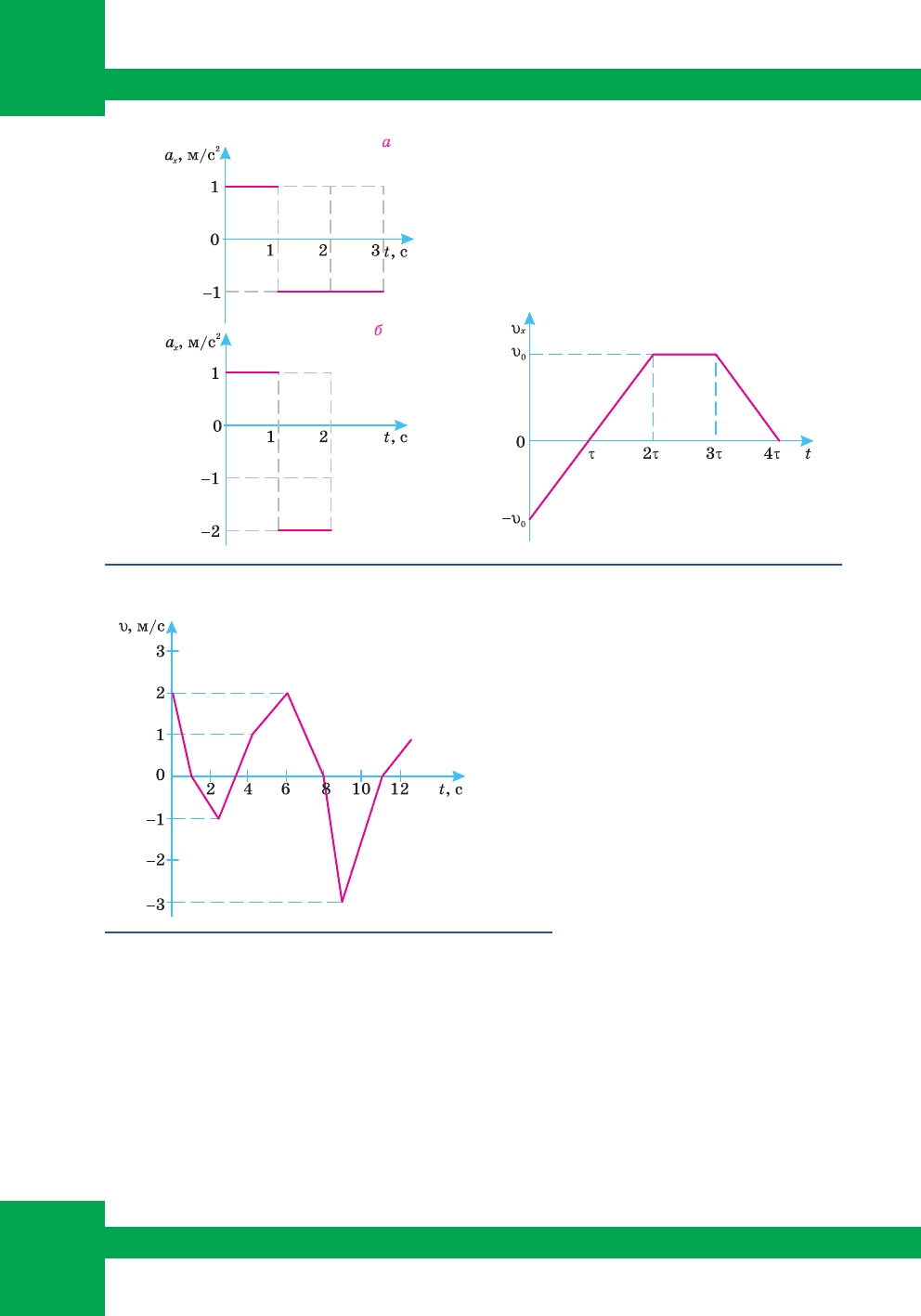
6. Çà ãðàô³êàìè çàëåæíîñò³ a
x
(t), íàâåäåíèìè íà ìàë. 61, à ³ 61, á, ïîáóäó-
âàòè ãðàô³êè υ
x
(t), ââàæàþ÷è, ùî ó ïî÷àòêîâèé ìîìåíò ÷àñó (t = 0) øâèäê³ñòü
ðóõó ìàòåð³àëüíî¿ òî÷êè äîð³âíþº íóëþ.
7. Ðóõè äâîõ àâòîìîá³ë³â ïî øîñå îïèñóþòüñÿ ð³âíÿííÿìè: x
1
= 2t + 0,2t
2
i
Ìàë. 58. Ãðàô³êè ïðîåêö³¿
øâèäêîñò³ òà ïðèñêîðåííÿ
Ìàë. 59. Äî çàäà÷³ 4 Ìàë. 60. Äî çàäà÷³ 5
60
Ð Î Ç Ä ² Ë 1
x
2
= 80 − 4t. Âñ³ âåëè÷èíè çàïèñàíî â Ѳ.
Îïèñàòè êàðòèíó ðóõó; âèçíà÷èòè ÷àñ
³ ì³ñöå çóñòð³÷³ àâòîìîá³ë³â; â³äñòàíü
ì³æ íèìè ÷åðåç 5 ñ; êîîðäèíàòó ïåðøî-
ãî àâòîìîá³ëÿ ó òîé ìîìåíò ÷àñó, êîëè
äðóãèé ïåðåáóâàâ íà ïî÷àòêó â³äë³êó.
Ðîçâ’ÿçàòè çàäà÷ó àíàë³òè÷íî ³ ãðàô³÷íî.
8. Ìàòåð³àëüíà òî÷êà
ðóõàºòüñÿ âçäîâæ â³ñ³ Õ ç³
øâèäê³ñòþ
υ
r
(ìàë. 62). Îäèí
ï³ä îäíèì íàêðåñëèòè ãðà-
ô³êè ïðîåêö³é ïðèñêîðåííÿ
a
x
(t), ïåðåì³ùåííÿ s
õ
(t) òà ïðî-
éäåíîãî øëÿõó l(t). Âèçíà÷è-
òè ñåðåäíº çíà÷åííÿ ìîäóëÿ
øâèäêîñò³ çà ÷àñ ðóõó â³ä t =
0 äî t = 2τ.
9. Íà ìàë. 63 íàâåäåíî
ãðàô³ê øâèäêîñò³ ò³ëà, ÿêå
ðóõàºòüñÿ ïðÿìîë³í³éíî. Íà
ÿêó ìàêñèìàëüíó â³äñòàíü â³ä
ïî÷àòêîâîãî ïîëîæåííÿ â³ä-
õîäèòü ò³ëî çà ÷àñ ðóõó?
10. Íàêðåñë³òü ãðàô³ê çàëåæíîñò³ êîîðäèíàòè â³ä ÷àñó äëÿ ïðÿìîë³í³éíîãî
ðóõó, ùî îäíî÷àñíî çàäîâîëüíÿº äâ³ âèìîãè: à) ïðîòÿãîì ³íòåðâàëó ÷àñó â³ä 2
äî 6 ñ ñåðåäíÿ øâèäê³ñòü ðóõó äîð³âíþº 5 ì/c; á) ìàêñèìàëüíà øâèäê³ñòü ïðî-
òÿãîì òîãî ñàìîãî ³íòåðâàëó ÷àñó äîð³âíþº 15 ì/c.
Ìàë. 61. Äî çàäà÷³ 6 Ìàë. 62. Äî çàäà÷³ 8
Ìàë. 63. Äî çàäà÷³ 9
