Yang X.-S. Introductory Mathematics for Earth Scientists

Подождите немного. Документ загружается.

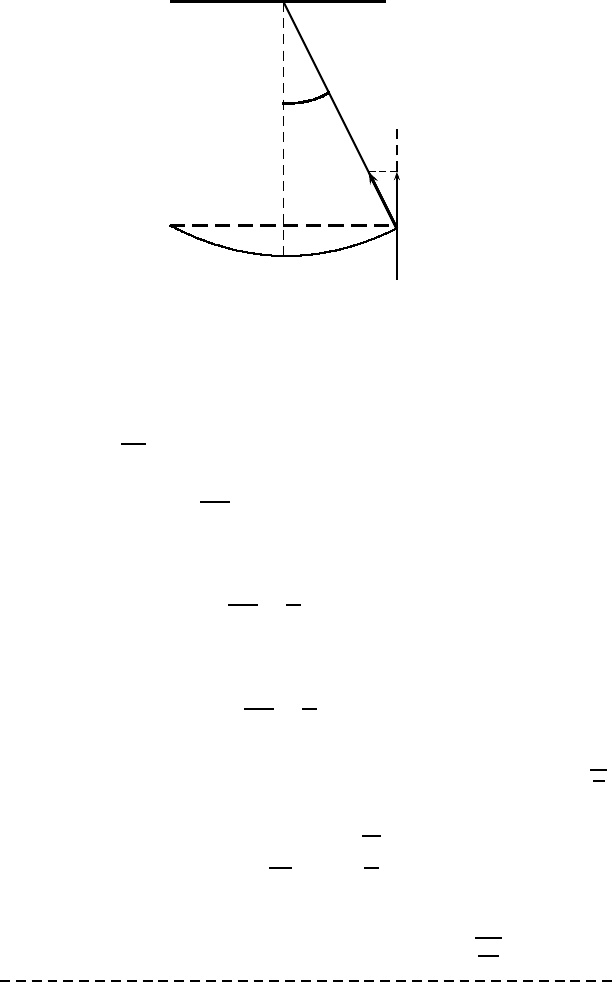
160 Chapter 11. Ordinary Differential Equations



Figure 11.1: A simple pendulum and its harmonic motion.

In th e horizontal direction, Newton’s second law F = ma implies that

the horizontal force −T sin θ must be equal to the mass m times the

acceleration L

. Now we have

m(L

) = −T sin θ ≈ −mg sin θ.

Dividing both sides by mL, we have

sin θ = 0.

Since θ is small, we have sin θ ≈ θ. Therefore, we ﬁnally have

θ = 0.

This is the equation of motion for a simple pendulum. From equation

(11.44), we know that the angular frequency is ω

= g/L or ω =

Thus the period of the pendulum is

T =

2π

= 2π

. (11.45)

We can see that the period is independent of the bob mass. For L = 1 m

and g = 9.8 m/s

, the period is approximately T = 2π

9.8

≈ 2 s.

Now we will try to ﬁnd the particular integral y

∗

(x) for the non-

homogeneous equation. For pa rticular integrals, we do not intend to

11.4 Higher-Order ODEs 161

ﬁnd the general fo rm; any sp e c iﬁc function or integral that satisﬁes the

original eq uation (11.29) will do. Befo re we can determine the partic-

ular integral, we have to use some trial functions, and such functions

will have strong similarity with the function f(x). For example, if

f(x) is a polynomial such as x

+ αx + β, we will try a similar form

∗

(x) = ax

+ bx + c and try to determine the coeﬃcients. Let us

demonstrate this by an example.

Example 11.6: In order to solve the diﬀerential equation

+ 5

− 6y = x − 2,

we ﬁrst ﬁnd its complementary function. From the earlier example, we

know that the complementary function can be written as

(x) = Ae

+ Be

−3x

For the particular integral, we know that f(x) = x −2, so we try the form

∗

= ax + b. Substituti n g it into the original equation

0 + 5a − 6(ax + b) = x − 2,

(−6a)x + (5a − 6b) = x − 2.

As this equality must be true for any x, so the coeﬃcients of the same

power of x on both sides of the equation s h ould be equ a l. That is

−6a = 1, (5a − 6b) = −2,

which gives a = −

, and b =

. So the general solution becomes

y(x) = Ae

+ Be

−3x

−

Similarly, if f(x) = e

αx

, we will try to y

∗

(x) = ae

αx

so as to deter-

mine a. In addition, we f(x) = sin αx or cos αx, we will attempt the

general form y

∗

(x) = a cos αx + b sin αx.

11.4 Higher-Order ODEs

Higher-order ODEs are more complicated to solve even when they a re

linear. In the special case o f higher-order ODEs where all the coeﬃ-

cients a

, ..., a

, a

are constants,

(n)

+ ... + a

+ a

y = f(x), (11.46)

162 Chapter 11. Ordinary Differential Equations

the solution procedure is identical to that for the s e c ond-order diﬀer-

ential equation we just discussed in the previous section. The general

solution y(x) a gain consists of two parts: the complementary function

(x) and the particular integral or particular solution y

∗

(x). We have

y(x) = y

(x) + y

∗

(x). (11.47)

The complementary function which is the solution of the linear

homogeneous equation with consta nt coeﬃcients can be written in a

generic form

(n)

+ a

n−1

(n−1)

+ ... + a

+ a

= 0. (11.48)

Assuming y = Ae

λx

where A is a constant, we get the characteristic

equation as a polynomial

+ a

n−1

(n−1)

+ ... + a

λ + a

= 0, (11.49)

which has n roots in the general case. Then, the solution can be ex-

pressed as the summation of various terms y

(x) =

k=1

if the

polynomial has n distinct zeros λ

, ...λ

. For complex roots, and com-

plex roots always occur in pairs λ = r ±iω, the corresponding linea rly

independent terms can then be replaced by e

[A cos(ωx) + B sin(ωx)].

The particular s olution y

∗

(x) is any y(x) that satisﬁes the original

inhomogeneous equation (11.46). Depending on the form o f the func-

tion f (x), the particular solutions can take various forms. For most of

the combinations of basic functions such as sin x, cos x, e

, a nd x

, the

method of undetermined coeﬃcients is widely use d. For f(x) = sin(αx)

or cos(αx), then we can try y

∗

= A sin αx + B sin αx. We then substi-

tute it into the original equation (11.46) so that the coe ﬃcients A a nd

B can be determined. For a polynomial f(x) = x

(n = 0, 1, 2, ...., N ),

we then try y

∗

= A + Bx + ... + Qx

(po ly nomial). For f (x) = e

∗

= (A + Bx + ...Qx

. Similarly, f(x) = e

sin αx or f (x) =

cos αx, we can use y

∗

= e

(A sin αx + B cos αx). Mor e general

cases and their particular solutions can be found in various textbooks.

A very useful technique is to use the method of diﬀerential operator

D. A diﬀerential operator D is deﬁned as

D ≡

. (11.50)

Since we know that De

λx

= λe

λx

and D

λx

= λ

λx

, so they a re

equivalent to D 7→ λ, and D

7→ λ

. Thus, any polynomial P (D) will

map to P (λ). On the other hand, the integral operator D

−1

is just the inverse of the diﬀerentiation. The beauty of the diﬀerential

operator form is that it can be factorised in the same way as for a poly-

nomial, then it can s olved us ing each factor separately. The diﬀerential

11.5 Applications 1 63

operator is very useful in ﬁnding out both the complementary functions

and particular integra l.

Example 11.7: To ﬁnd the particular integral for the equatio n

0000000

+ 22y = 15e

, (11.51)

we get

+ 22)y

∗

= 15e

, (11.52)

∗

+ 22)

. (11.53)

Since D

) = 2

or D

7→ λ

= 2

, we have

∗

15e

+ 22

15e

150

. (11.54)

This method also works for sin x, cos x, sinh x and others, and this is

because they are related to e

λx

via sin θ =

iθ

− e

−iθ

) and cosh x =

+ e

−x

)/2.

Higher-order diﬀerential equations can conveniently be written as a

system of diﬀerential equations. In fact, an nth-order linear equation

can always be written as a linear system of n ﬁrst-order diﬀerential

equations. A linear sys tem of ODEs is more suitable for mathematical

analysis and numerical integration.

11.5 Applications

We have studied the solution of ordinary diﬀerential equations. Let us

see how they are applied in modelling real-world problems.

11.5.1 Climate Changes

A simple CO

model with a constant rate w of emission is governed by

+ p

+ qA = rw, (11.55)

where A(t) = C−A

is the exce ss CO

concentration in the atmosphere.

That is the diﬀerence between the a c tual CO

concentration C ab ove

the pre-industrial CO

concentration A

with an average value of A

280 ppm. p and q are the combined reservoir transfer coeﬃcients, and

r is a constant. This simple model is based on the models by Holter et

al and Keeling’s three-reservoir model for carbon dioxide cycle.

164 Chapter 11. Ordinary Differential Equations

By assuming that A = e

λt

and substituting into the homogeneous

equation

+ p

+ qA = 0, (11.56)

we have

+ pλ + q = 0, (11.57)

whose solution is

= −

(1 +

1 −

), λ

= −

(1 −

1 −

). (11.58)

For typical values of p = 1.007/year, q = 0.0123/year

, we have

≈ −0.995, λ

≈ −0.0124. (11.59)

Therefore, the homogeneous solution can be written as

A = ae

+ be

. (11.60)

Since |λ

|  |λ

|, the ﬁrst term with e

−λ

will become very small if t

is large. In climate dynamics, we are often dealing with the timescale

of hundreds of years, so we can essentially use the approximate solution

A ≈ be

. (11.61)

The particular integral A

∗

can be obtained by assuming the form

A = K where K is the undetermined coeﬃcient, we have dA/dt = 0,

A/dt

= 0, and

qK = rw, (11.62)

K =

. (11.63)

Therefore, the general solution becomes

A = be

. (11.64)

The typical timescale τ for this system can be deﬁned as τ = 1/|λ

| =

1/0.0124 ≈ 80 years, so that the solution becomes

A = be

−t/τ

. (11.65)

Using the typical value of r = 0.884/year, and initial value A(0) = 0

ppm at t = 0, and w ≈ 0.014/year ×A

≈ 3.92 ppm/year (the e sti-

mated level of emission in year 2000, equivalent to about 8.4 giga-

tons/year ), we have

b × e

αr

= 0, (11.66)

11.5 Applications 1 65

b = −

The solution now becomes

A(t) =

(1 − e

−t/τ

), (11.67)

or after plugging the numbers, we have

A(t) ≈ 281.7(1 − e

−t/80

). (11.68)

So the long-term excess of CO

will be 281.7 ppm, thus the actual

will be 281.7 + A

≈ 561.7 ppm, which is about twice the pre-

industrial concentration. Even with this constant rate, we can r e ach

the maximum in 2 00 years. If the emission is increased to a higher

level at 20 giga tons/year (in the year 2100), then the eq uilibrium CO

concentration will approach 670 + A

= 950 ppm, and we can expec t to

reach to twice the pre-industria l level more quickly. This simple model

shows that we have to reduce the CO

signiﬁcantly over a long pe riod.

11.5.2 Flexural Deﬂection of Lithosphere

The governing equation for the lithosphere deﬂection u under a load

P (x) can be written as

+ g(ρ

− ρ

)u = P (x), (11 .69)

where ρ

, and ρ

are the densities of the mantle and water, respec-

tively. g is the acceleration due to gravity, and D is the ﬂexural rigidity

deﬁned as

D =

12(1 − ν

)

, (11.70)

where E and ν are Young’s modulus and Poisson’s ratio of the litho-

sphere, respectively. H is the thicknes s of the lithosphere (see Fig.

11.2). A spec ial case of the lo ad variation is periodic, that is

P (x) = ρ

sin

2πx

, (11.71)

where λ and h

are the typical wavelength and amplitude of the topo-

logical variations , respectively. ρ

is the density of the load.

Now let us solve this equation and also provide the appropriate

boundary conditions. The homogeneous equation becomes

0000

+ g(ρ

− ρ

)u = 0, (11.72)

166 Chapter 11. Ordinary Differential Equations

Figure 11.2: Deﬂection of the lithosphere as a thin shell.

whose characteristic equation (using u = e

ωx

) becomes

Dω

+ g(ρ

− ρ

) = 0, (11.73)

whose solution is

ω =



−g(ρ

− ρ

)



√

−1

ρ(ρ

− ρ

)

. (11.74)

Since

√

−1 = i and

√

−1 =

√

i =

√

(±1 ± i), (11.75)

and they correspond to four solutions

1,2

= −(1±i)β, ω

3,4

= (1±i)β, β =

(ρ

− ρ

, (11.76)

where we have absorbed the factor 1/

√

2 =

1/4 into β. We have the

complementary function

u = Ae

(−β+iβ)x

+ Be

(−β−iβ)x

+ Ce

(β+iβ)x

+ De

(β−iβ)x

= Ae

−βx

[cos βx + i sin βx] + Be

−βx

[cos(−βx) + i sin(−βx)]

+Ce

βx

[cos βx + i sin βx] + De

βx

[cos(−βx) + i sin(−βx)]

= e

−βx

[(A + B) cos(βx) + i(A −B) sin(βx)]

βx

[(C + D) cos(βx) + i(C − D) sin(βx)] (11.77)

where A and B are arbitrary constants. Here we have used sin(−βx) =

−sin(βx). This expression can be r e written more compactly as

u = e

−βx

[P cos(βx)+ Q s in(βx)]+ e

βx

[U cos(βx)+V sin(βx)], (11.78)

where P = A + B, Q = i(A − B), U = C + D and V = i(C − D) are

the new constants.

11.5 Applications 1 67

Since the amplitude of the deﬂection must b e ﬁnite, the solutions

3,4

are not poss ible because e

βx

→ ∞ will grow exponential as x → ∞.

Therefore, U = V = 0. Only solutions ω

1,2

are acceptable.

For the particular integral, let us try the form

∗

= u

sin(

2πx

). (11.79)

After substituting into the original equation, we have

(

2π

)

sin(

2πx

) + g(ρ

− ρ

sin(

2πx

) = ρ

sin(

2πx

After dividing both sides by sin(2πx/λ), we have

[D(

2π

)

+ g(ρ

− ρ

)] = ρ

, (11.80)

[D(

2π

)

+ g(ρ

− ρ

)]

(

2π

)

(ρ

−ρ

)

, (11.81)

which is the well-known Turcotte-Schubert solution.

So the general solution now becomes

u = e

−βx

[A cos(βx) + B sin(βx)]

[

(

2π

)

(ρ

−ρ

)

]

sin

2πx

. (11.82)

The constants A and B should be determined by boundary conditions.

If we are mor e interested in the deformation over a la rge scale, then x

is large. So β > 0 implies that e

−βx

→ 0 as x → ∞. This means that

the particular integral is more important in this case.

Here we can discuss two asymptotic cases even without determining

A and B. Fro m the above solution, we know that

(

2π

)

= 1, (11.83)

deﬁnes a critical wave length λ

∗

, called the ﬂexural wavelength

∗

= 2π

. (11.84)

If λ  1, we have

(

∗

)

(ρ

−ρ

)

≈

(ρ

− ρ

)

, (11.85)

168 Chapter 11. Ordinary Differential Equations

which is essentially the solution at the isostatic equilibrium.

On the other hand, if λ  λ

∗

, we have

(

∗

)

(ρ

−ρ

)

≈ h

(

∗

)

→ 0. (1 1.86)

This means that the lithosphere is extremely rigid and the deﬂection

on the short wavelength is neg ligible.

11.5.3 Glacial Isostatic Adjustment

The behaviour of solid and/or molten rocks will be very diﬀerent if we

look at them on diﬀerent timescales. On a geological timescale, they

are highly viscous. In fact, viscosity is important for many phenomena

in earth sciences, including the mantle convection, post-glacier rebound

and isostasy. The last glacial period ended about 10,000 to 1 5,000 years

ago. During the ice age, thick glacier s caused the deformation of the

surface of the crust, thus depleting the mantle materials or causing it

to ﬂow away. When the ice age ended, the retreat of the glacier would

lead to the rebound or uplift of the depre ssed crust, accompanied by

the ﬂow back of the mantle materials. This process is similar to the

process of dipping a ﬁnger brieﬂy in soft or liquid chocolate. As the

mantle is highly viscous with a viscosity o f about 10

Pa s, the rebound

is a very slow process lasting several thousands to tens of thousands of

years. This process is called pos t- glacial rebound, or glacial isostatic

adjustment.

The uplift is typically a few millimetres a year with a relaxation time

of a few thousand years fo r the post-glacial rebounds in north Europe

and north America. Under the assumptions that the uplift process is

similar to a viscoelastic relaxatio n process, the governing equation in

the simplest case c an be written as

∂h

∂t

= −

(h − h

)

, (11.87)

where h is the uplift, and h

is the total amount of uplift which will

eventually be achieved as t → ∞. τ is the characteristic timescale of

relaxation or response timescale

τ =

4πη

gλ

, (11.88)

where η a nd ρ

are the viscos ity (or dynamic viscosity) and density of

the mantle, respectively. g is the acceleration due to gravity, a nd λ is

the typical wavelength of the uplift.

Equation (11.87) is a simple ﬁrst-order diﬀerential equation, its so -

lution can be obtained by direct integration if we use

z = h − h

, (11.89)

11.5 Applications 1 69

which is the remaining uplift to be achieved. Since

, the gov-

erning equation (11.87) beco mes

= −

, (11.90 )

which leads to

dz = −

dt, or ln z = −

+ A, (11.91)

where A is the constant of integration. This gives

z = Be

−t/τ

, (11.92)

where B = e

. At t = 0, we have h(0) = 0 so that z(0) = B = −h

The solution now becomes

z = −h

−t/τ

, (11.93)

and the uplift is

h(t) = z + h

= h

(1 − e

−t/τ

). (11 .94)

Therefore, we have h → h

as t → ∞ as expected.

From ﬁeld observations , we now know that the relaxation time for

the Fennoscandian uplift in north Europe is about 4 900 to 6750 years.

Let us see how equation (11.88) ﬁts. From the typical values of η = 10

Pa s, ρ

= 3 300 kg/m

, λ = 2000 km= 2 × 10

meters, and g = 9.8

m/s

, we have

τ =

4πη

ρgλ

4π × 10

3300 × 9.8 × 2 × 10

≈ 1.94 × 10

seconds ≈ 6160 years, (11.95)

where we have used 1 year= 3.15 × 10

seconds. This is about right.

Conversely, if we know the relaxation time τ, we can estimate the

viscosity of the mantle. If we us e the average ¯τ ≈ 5500 years= 1.73 ×

seconds, we have

η =

¯τρgλ

4π

≈

1.73 × 10

× 3300 × 9.8 × 2 × 10

4π

≈ 0.9 × 10

Pa s, (11.96)

which is a better estimate than 10

Pa s.

In addition, we could measure the uplifts h

and h

at two diﬀerent

times t

and t

, respectively, we can calculate the ultimate uplift h

From a ny two observations

= h

(1 − e

−t

/τ

), (11.97)