Yang X.-S. Introductory Mathematics for Earth Scientists

Подождите немного. Документ загружается.

180 Chapter 13. Geostatistics

variable. Other continuous random variables are the temperature vari-

ations in a year, the stress variations in an earthquake zone, and the

velocity of a drifting plate.

The set of all the possible outcomes forms the sample space, and

the elements of a sample space are called outcomes. Each subset of

a sample s pace is called an event. For example, rolling a die has 6

possible outcomes, so the sample s pace is simply the set of all the

possible outcomes: Ω = {1, 2, 3, 4, 5, 6}. An event such as A = {2, 3, 5}

is the event that correspo nds to the case when the face values of the

die are prime numbers.

Probability P is a number or a n expected freq uency assigned to an

event A that indicates how likely it is that the event will occur when a

random experiment is performed. In order to show the probability P

is associated with event A, we usually write this proba bility as P (A).

If we conduct a large number of fair trials such as tossing a coin 5,000

times, the probability of an event such as heads can be calculated by

P (A) =

(number of outcomes in the event A)

Ω

(total number of outcomes)

. (13.2 )

The total sum of all the probabilities of all the possible outcomes must

be 1. For example, if we toss a coin 5000 times, the heads appear

2507 times. The probability of heads is P (H) = 2507/5000 = 0.5014.

As there must be (5000 − 2 507) = 2493 tails appear, the probability

of tails is P (T ) = 2493/500 0 = 0.4986. The total pro babilities are

P (H) + P (T ) = 0.5014 + 0.4986 = 1.0.

Two events are said to be independent if one event is not aﬀected

by whether or not the other event occurs. In this case, the probability

P of both events occ urring is the product of individual pr obabilities

P = P (A)P (B), (13.3)

where P (A) and P (B) are the probabilities for events A and B, re-

sp e c tively. For example, if we toss a coin and roll a die a t the same

time, what is the probability that both a head and the numb e r 5 oc-

cur? Let A be the event of a head, and B be the event of numbe r 5 as

the outcome of ro lling a die. We have P (A) = 1/2 and P (B) = 1/6,

therefore we have the pr obability of both events occurring at the same

time P = P (A)P (B) = (1/2) × (1/6) = 1/12.

Each value or outcome of a random variable may occur with certain

probability, and the probability may vary. In this case, we use a proba-

bility density function p(x) to represent how the probability var ies with

x. If there are n possible outcomes x

for a discrete random variable,

we have

i=1

p(x

) = 1. (13.4)

13.1 Random Variables 181

The function p(x) is also known a s the distribution function. When

the variable is discrete, the distribution is called discrete distribution.

If a random variable is continuous, the probability function f (x) is

usually deﬁned for a range of values x ∈ [a, b]. The probability is often

associated with an interval (rather tha n a distinct value) (x, x + dx]

or the random variable takes the value x < X ≤ x + dx where dx is a

small increment. The convention we used here is that we use the Roman

capital letter to denote the random variable and its corresponding small

lower case to denote its values.

The probability function for a continuous random variable is also

called the probability density function (pdf). In this case, all the prob-

abilities should be added to unity. That is

p(x)dx = 1. (13.5)

A good example of disc rete distribution functions is the Poisson distri-

bution

p(k; λ) =

−λ

, (λ > 0), (13.6)

where k = 0, 1, 2, 3, ... a nd λ is the parameter of the distribution. An

excellent example of continuous distribution functions is the Gaussian

or normal distribution

p(x) =

√

2π

−

(x−µ)

2σ

, −∞ < x < ∞ (13.7)

where x is continuous. µ and σ are two parameters. The normal distri-

bution with µ = 0 and σ = 1 is called the standard normal distribution.

13.1.2 Mean and Variance

Two main measures for a random variable X with a given probability

distribution function p(x) are its mean and variance.

The mean µ is also called the expected value of the distribution,

denoted by E[X] and is deﬁned by

µ ≡ E(X) =

xp(x)dx, (13.8)

for a continuous distr ibution and the integration is within the integra-

tion limits. Other notations such as <X >≡

X are also interchangeable

with µ. If the random variable is discrete, then the integration becomes

the summation

µ =

p(x

). (13.9)

182 Chapter 13. Geostatistics

The variance, denoted by σ

≡ var[X] is the mean of the deviation

squared (X − µ)

. That is

≡ var[X] = E[(X − µ)

] =

Ω

(x − µ)

p(x)dx, (13.10)

where Ω is the sample space. The sq uare root of the variance σ =

var[X] is called the standard deviation, which is denoted by the

symbol σ. Obviously, for a discrete distribution, the variance simply

becomes a sum

(x − µ)

p(x

). (13.11)

The mean and variance of the Poisson distribution are both λ.

Example 13.1: Let us now try to calculate the mean and variance of

the normal distribution

p(x) =

√

2π

−

(x−µ)

2σ

, −∞ < x < +∞.

The mean is given by

E[X] =

∞

−∞

xp(x)dx.

By se tting u = x − µ, we ha ve x = u + µ a n d du = dx. In addition,

the inﬁnite limits of the integration remain the same by shifting any ﬁnite

amount µ. T h e above equation becomes

E[X] =

√

2π

∞

−∞

(u + µ)e

−u

/2σ

du =

√

2π

+ µI

where

∞

−∞

−u

/2σ

du, I

∞

−∞

−u

/2σ

du.

Using

erf(x) =

√

−u

du,

and letting v = u/

√

2σ, we have

= σ

√

∞

−∞

−v

dv = σ

π/2 erf(v)



∞

−∞

= σ

√

2π,

where we have used erf(∞) = 1 and e rf(−∞) = −1.

Similarly, from udu =

d(u

), we have

∞

−∞

−u

/2σ

du =

∞

−∞

−u

/2σ

d(u

)

13.2 Sample Mean and Variance 183

= σ

∞

−∞

−v

= σe

−v



∞

−∞

= 0.

Therefore, the mean becomes

E[X] =

µI

√

2π

= µ.

The variance is given by var[X] or

E[(x − µ)

∞

−∞

(x − µ)

p(x)dx=

√

2π

∞

−∞

(x − µ)

−(x−µ)

/2σ

dx.

Setting w = (x − µ)/

√

2σ, we have dx = σ

√

2dw, a n d we have

var[X] =

√

2σ2σ

√

2π

∞

−∞

−w

dw =

2σ

√

∞

−∞

−w

dw.

Using the result given in an earlier example in the chapter on integration

∞

−∞

−w

dw =

√

we have

var[X] =

2σ

√

= σ

This proves that the mean of th e normal distribution is µ and the variance

is σ

so that the standard deviation is σ.

If we know the distribution function, it is always possible to calcu-

late its mean and variance, though the integration is not an easy task.

In earth sciences, we have often collected a lot of data, but we do not

know exactly what the distribution is. In this case, we have to dea l

with sample mean and sample variance.

13.2 Sample Mean and Variance

If a sample consists of n independent obs e rvations x

, x

, ..., x

a random variable X such as the noise level, the sample mean can be

calculated by

¯x =

i=1

+ x

+ ... + x

), (13.12)

which is the arithmetic average of the values of the data x

184 Chapter 13. Geostatistics

The sample variance is deﬁned by

n − 1

i=1

− ¯x)

. (13.13)

It is worth pointing out that the factor is 1/(n−1) not 1/n because only

1/(n − 1) will give the correct and unbiased estimate of the variance.

The other way to think about this factor is that we need at least one

value to estimate the sample mean, and we need at least two values

to estimate the varia nce . Therefore, for n observations, only (n − 1)

diﬀerent values of variance can be obtained to estimate the total sample

variance.

Example 13.2: The average drifting velocity of the tectonic plate can

be estimated using the data from Hawaiian Islands, formed as a result of

a series of volcanic eruptions by a giant hot spot. The distance data are

as follows: Kauai to Oahu is about 180 km with an age diﬀerence of 1.9

Ma (million years); Oahu to Molakai is 120 km with an age diﬀerence of

1.27 Ma; Molakai to Maui is 80 km with an age diﬀerence of 0.7 Ma; and

Maui to Hawaii is 125 km with an age diﬀerence of 1 Ma. So th e velocity

of the plate movement from Kauai to Oahu is

v =

180 × 100 0

1.9 × 10

m/year ≈ 0.095 m/ year = 9.5 cm/year.

Similarly, o th e r velocities are 9.4, 11.4 , 12.5 cm/year.

The mean velocity of this plate movement is

¯v =

(9.5 + 9.4 + 11.4 + 12.5) = 10.7cm/year.

The variance of the velo c ity (for n = 4) is

= var[v] =

4 − 1

[(9.5 − 10.7)

+ (9.4 − 10.7)

+(11.4 − 10.7)

+ (12.5 − 10.7)

] ≈

× 6.86 ≈ 2.3.

Therefore, the standard deviation is σ =

√

2.3 ≈ 1.5 c m/year.

13.3 Propagation of Errors

Any experiment will have measurement er rors or uncertainty. There

are two main type of errors: system errors, and random errors. System

errors are errors that are systematic, either known or unknown, which

will aﬀect the measur e ment or observations in a systematic way. System

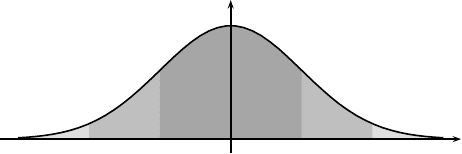
13.3 Propagation of Errors 185

+σ−σ +2σ−2σ

34.15%34.15%

Figure 13.1: Standard deviation and conﬁd ence interval.

errors can b e reduced by good design of exper iments and analysis of

contributing factors. Random err ors are undeterministic, which are

unavoidable but can be minimised by us ing higher-precision equipment.

The words ‘errors’ and ‘uncertainty’ are almost synonymic and thus

interchangeable. However, we often use uncertainty to chacterise the

variations of errors, while we use erro rs to measure the diﬀerence be-

tween the measured and the true value. Since the true value is rarely

known, the e rrors are not easy to estimate. There are two ways to

deﬁne errors: absolute error and relative error.

The absolute error is simply the diﬀerence between the observed

and the true value or expected value. For example, we know that

density of water is 1000 kg/m

(expected value) at room temperature.

If we get a value of 990 k g/m

in an experiment, then the error of this

exp e riment is 990 −1000 = −10 kg/m

. The relative error is the ratio

of the diﬀerence divided by the expected value. Therefore, the relative

error in this experiment is | − 10|/1000 = 1%. The percentage error is

the relative e rror times 100%. The advantage of relative errors is that

they have no units.

In statistics, we often use the sta ndard deviation σ

to characterise

the uncertainties or errors of the quantity y. The standard way to write

the results of measurements is

y = µ

± σ

, (13.14)

where µ

is the mean. For example, if we measured the acceleration of

gravity at the Earth’s surface at a particular location is 9.80m/s

with

an uncertainty or standard deviation of 0.05 m/s

, we write

g = 9.80 ± 0.05 m/s

. (13.15)

It is worth pointing out that the form should contain the meaningful

signiﬁcant ﬁgures. In this case, we should not write it as g = 9.800 ±

0.050 or 10 ± 0.05.

The standa rd expression µ

± σ

is associated with the conﬁdence

interval (see Fig. 13.1). This expression suggests that there is about

68.3% of chance that the observations will be in this range. The reason

186 Chapter 13. Geostatistics

is that the total a rea under the normal distribution curve is 1, and the

area under the curve between −σ to +σ is

A =

−σ

√

2π

−x

/2σ

dx =

√

2π

−x

/2σ

dx, (13.16 )

where we have used the fact that e

−x/2σ

is an even function. Using

u = x/

√

2σ, we have dx =

√

2σdu so that

√

2π

√

2σe

−u

du=

√

−u

du= erf(1/

√

2), (13.17)

which is about 0.6827. This means that there is 0.6827 ≈ 68.3% chance

that the data will fall in the range of [µ

−σ

, µ

+ σ

]. In other words,

there is about 34.1 5% chance tha t it will be in the range from µ

+ σ

, and the same chance in the range from µ

−σ

to µ

. Another

way of saying this is that the conﬁdence level is 68.3%. If we write

the results as µ

+ 2σ

, then the conﬁdence level now becomes 95.4%

due that the fac t that the area under the cur ve between −2σ to 2σ is

erf(

√

2) ≈ 0.954.

For a given va riance σ

of x for n data points

n − 1

i=1

− ¯x)

, (13.18)

where ¯x =

i=1

is the sample mean of x

(i = 1, 2, ..., n), we can

calculate the va riance of a function y = f (x). We know from the basic

deﬁnition that

n − 1

i=1

−

, (13.19)

where

f is the mean and f

= f(x

). Using ∆f =

∆x = f

∆x and

setting ∆f = f

−

f, we have

−

f) = (x

− ¯x)

. (13.20)

The variance now becomes

n − 1

i=1

− ¯x)

n − 1

i=1

− ¯x)

(

)

. (13.21)

In the case of

is independent of x

or if we evaluate the derivative

at x = µ

≈ ¯x, we have

= (

)

n − 1

i=1

− ¯x)

= σ

(



¯x

)

, (13.22)

13.3 Propagation of Errors 187

where |

¯x

means that derivative is evaluated using x = ¯x. This is the

formula for error propagation.

If there are measurements of two independent variables x and y,

we can derive similar formulae for the propagation of erro rs for any

function z = f(x, y). From the to tal derivatives, we k now that

∆f =

∂f

∂x

∆x +

∂f

∂y

∆y. (13.23)

Setting ∆f = (f

−

f), ∆x = x

− ¯x and ∆y = y

− ¯y where ¯y is the

mean, we have

−

f) = (x

− ¯x)

∂f

∂x

+ (y

− ¯y)

∂f

∂y

. (13.24)

Taking the squares and sums, we have

n − 1

i=1

−

n − 1

i=1

− ¯x)

∂f

∂x

+ (y

− ¯y)

∂f

∂y

n − 1

i=1

− ¯x)

(

∂f

∂x

)

n − 1

i=1

− ¯y)

(

∂f

∂y

)

n − 1

i=1

− ¯x)(y

− ¯y)

∂f

∂x

∂f

∂y

. (13.25)

By deﬁning the covariance of x and y as

n − 1

i=1

− ¯x)(y

− ¯y), (13.26)

and evaluating the derivatives at x = ¯x and y = ¯y, we then have

n − 1

i=1

−

= σ

(

∂f

∂x

)

+ σ

(

∂f

∂y

)

+ 2σ

∂f

∂x

∂f

∂y

. (13.27)

In the case when x and y are independent so that σ

= 0, we have

= σ

(

∂f

∂x

)

+ σ

(

∂f

∂y

)

. (13.28)

For example, if z = kx

where k, α and β are constants, we have

= σ

(kαx

α−1

)

+ σ

(kβx

β−1

)

. (13.29)

Dividing both sides by z

= (kx

)

and evaluating the derivatives

at x = µ

, y = µ

and z = µ

, we have the relative errors

(

)

= (

ασ

)

+ (

βσ

)

. (13.30)

188 Chapter 13. Geostatistics

Example 13.3: An experiment gi ves the following empirical equation

z = f(x, y) = x − y,

with σ

= 0 .3 and σ

= 0 .4. That is x = 2.5 ± 0.3 and y = 1.0 ± 0.4.

What is the standard deviation σ

of z = f (x, y)? We know that

∂z

∂x

= 1,

and

∂z

∂y

= −1. From (13 .28), we have

= σ

(

∂z

∂x

)

+ σ

(

∂z

∂y

)

= 0.3

× 1

+ 0.4

× (−1)

= 0.25.

Therefore, the standard derivation σ

is σ

√

0.25 = 0.5. As the mean

= 2.5 − 1.0 = 1.5, we have z = 1.5 ± 0.5.

As a further example, let us estimate the speed of sound using v = s/t.

From (13.30), we have α = 1 and β = −1. If the measu red distance is

s = 500 ± 25 m, and the time taken is 1.50 ± 0.10, we then have

(

1 × 25

500

)

+ (

−1 × 0.10

1.5

)

≈

√

0.0069 ≈ 0.08.

As µ

= 50 0/1.5 ≈ 333, we now get σ

= µ

×0.08 ≈ 27. Therefore, we

have v = 333 ± 27 m/s.

If we have N observations for the same quantity x each with the

same uncertainty σ

, we have

µ =

+ x

+ ... + x

. (13.31)

Since

∂µ

∂x

= 1/N, we get

=σ

(

∂µ

∂x

)

+ ... + σ

(

∂µ

∂x

)

=σ

(

)

+ ... + σ

(

)

, (13.32)

which implies that σ

= σ

√

N. That is to say, more measurements

will reduce the error in the mean, though the standard derivation σ

remains the same.

13.4 Linear Regression

For experiments and observations, we usually plot one variable such as

pressure or price y against another va riable x such as time or spatial

coordinates. We try to present the data in such a way that we can see

some trend in the data. For a set of n data points (x

, y

), the usual

practice is to try to draw a straight line y = a+ bx s o that it represents

13.4 Linear Regression 189

, y

)

y = a + bx

Figure 13.2: Least square and th e best ﬁt line.

the major trend. Such a line is often called the r e gression line or the

best-ﬁt line as shown in Figure 13.2.

The method of least squares is to try to determine the two param-

eters a (intercept) and b (slope) for the regression line from n data

points. Assuming that x

are known more precisely and y

values obey

a normal distribution p(y

) ∝ exp{−[y

− f(x

)]

/2σ

} around the po-

tential best ﬁt line with a variance σ

, the best ﬁt can be obtained by

maximising the likelihood P deﬁned as

P = p(y

) × p(y

) × ... × p(y

)

≡

i=1

p(y

) = A exp

−

2σ

i=1

− f(x

)]

, (13.3 3)

where A is a c onstant, and f(x) is the function for the regression

[f(x) = a + bx for a simple linear regression].

The essence of the method o f least squares is to maximise the prob-

ability P by choosing the appropriate a and b. The maximisatio n of P

is equivalent to the minimisation of the exponent ψ

ψ =

i=1

− f(x

)]

. (13.34)

We see that ψ is the s um of the squares of the dev iations 

= (y

−

f(x

))

where f(x

) = a + bx

. The minimisation means the least sum

of the squares, thus the name of the method of least squares.

In order to minimise ψ as a function of a and b, its derivatives s hould

be zero. That is

∂ψ

∂a

= −2

i=1

[y − (a + bx

)] = 0, (13.35)

and

∂ψ

∂b

= −2

i=1

− (a + bx

)] = 0. (13.36)