Янчуковская Е.В., Ушакова Н.И. Математическое моделирование химических реакторов

11

II.

выхвх

ТТТ 

– лабораторные реакторы с малым объемом или специально

организованным тепловым режимом,

выхвх

VV 

– реакция с изменением

числа молекул в газовой фазе. В этом случае тепловой баланс исключается,

материальный баланс – уравнения (1.2). Примеры решения: 3 и 4.

III.

выхвх

ТТТ 

– адиабатические (или политропические) реакторы,

VVV

выхвх



– например, реакция в жидкой фазе. В этом случае тепловой

баланс составляется по уравнению (1.8), материальный баланс – уравнение

(1.4). Пример решения: 5.

IV.

ТТТ

выхвх



– адиабатические (или политропические) реакторы,

выхвх

VV 

– реакция с изменением числа молекул в газовой фазе. В этом

случае тепловой баланс – уравнение (1.6), материальный баланс – уравне-

ние (1.2). Пример решения: 6.

Алгоритмы «Прямая задача» используют результаты предшествующих

этапов анализа химико-технологического процесса (ХТП) (например, входные

сопряжения модуля для примера 5) и, в свою очередь, служат основой для ре-

шения более сложных обратных и оптимизационных задач.

Таким образом, постановка и решение прямой задачи для стационарного

режима работы реактора идеального перемешивания (гомогенные реакции) –

это формирование и решение систем алгебраических уравнений различной

сложности. Метод решения выбирается в зависимости от сложности уравнений.

Пример 1. В лабораторном реакторе идеального перемешивания в стацио-

нарном режиме проводится газофазная гомогенная мономолекулярная реакция из-

вестного механизма:

C

k



2

BА

k



1

выхвх

ТТТ 

D

k



3

VVV

выхвх



12

Заданы:

 

321 ,,jk

j



– константы скорости стадий (результат кинетического анализа), с

-1

,

 

D,C,B,AiC

i

вх



– концентрации компонентов смеси на входе в реактор, моль/м

3

,

вх

V

– объемная скорость входного потока, м

3

/с.

Определить состав смеси на выходе из реактора

 

D,C,B,AiC

i

вых



.

Решение. Тепловой баланс из рассмотрения исключается. Основа покомпо-

нентного материального баланса – уравнение (1.4)

0

1



ii

i

вх

R)СС(

τ

Скорости стадий реакции:

A

Ckr 

11

B

Ckr 

22

B

Ckr 

33

Скорость реакций по компонентам:

1

rR

A



321

rrrR

B



2

rR

C



3

rR

D



Математическое описание реактора (формула (1.4)):

 

0

1



AA

A

вх

CkСС

τ

 

0

1

321



BAB

B

вх

CkkCkСС

τ

 

0

1

2



BC

C

вх

CkСС

τ

(1.9)

 

0

1

3



BD

D

вх

CkСС

τ

Система (1.9) представляет собой простые алгебраические уравнения, реше-

нием которых являются концентрации компонентов реакционной смеси на выходе

τk

С

A

вх

A





1

13

 

32

1

1 kkτ

τCkC

C

A

В

вх

B







τCkCC

В

С

вхC



2

(1.10)

τCkCC

В

D

вхD



3

TR

E

jj

j

ekk







0

,

j

= 1, 2, 3

V

Vr

τ 

На основе полученного решения составляется расчетный модуль прямой за-

дачи. Модуль позволяет получить зависимости состава выходного потока от време-

ни пребывания (или объемной скорости входного потока) и от температуры реакции,

а также подобрать условия

 

Т,τ

для достижения заданной степени превращения

исходного вещества или максимального выхода целевых продуктов. Этот модуль

можно использовать в обратных задачах, при подборе

0

j

k

,

j

E

, а также в оптимиза-

ционных задачах при определении оптимальных условий проведения реакции

 

опт

i

вх

C,T,V

.

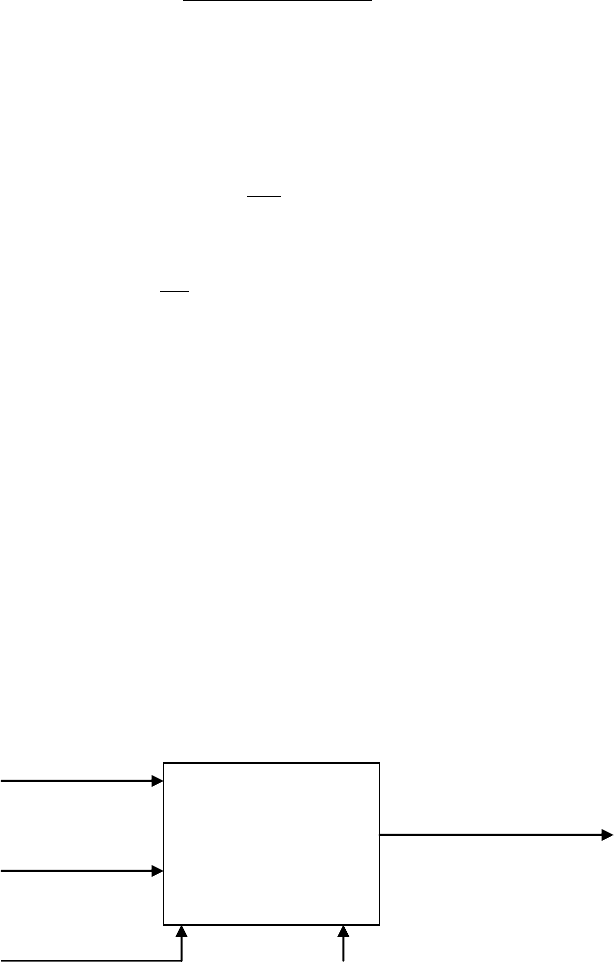
Рис. 2. Расчетный модуль компьютерного решения прямой задачи для примера 1

Пример 2. В лабораторном реакторе идеального перемешивания в стацио-

нарном режиме проводится газофазная гомогенная мономолекулярная обратимая

реакция известного механизма:

СВА 

21

выхвх

ТТТ 

-2

VVV

выхвх



Модуль

Прямая задача

для примера 1

Vr

D,C,B,Ai,CC

i

вых



выхвх

VVV 

321

0

,,j,E,k

jj



D,C,B,AiC

,iвх



выхвх

TTT 

14

Заданы:

 

21,jk

j



– константы скорости стадий (результат кинетического анализа), с

-1

,

2





k

K

P

– константа равновесия как функция температуры и давления (резуль-

тат термодинамического анализа),

 

C,B,AiС

i

вх



– концентрации компонентов смеси на входе в реактор, моль/м

3

,

вх

V

– объемная скорость входного потока, м

3

/с.

Определить состав смеси на выходе из реактора

 

C,B,AiС

i

вых



.

Решение. Основа покомпонентного материального баланса – уравнение (1.4).

Скорости стадий реакции:

A

Ckr 

11

B

Ckr 

22

С

Ckr 

 22

или

С

P

C

K

k

r 



2

Скорость реакции по компонентам:

1

rR

A



221 

 rrrR

B

22 

 rrR

C

Математическое описание реактора (формула (1.4)):

 

0

1



AA

A

вх

CkСС

τ

 

0

1

2

21

















P

C

BAB

B

вх

K

C

CkCkСС

τ

(1.11)

 

0

1

2

















P

C

BC

C

вх

K

C

CkСС

τ

Решение математического описания:

τk

С

А

вх

А





1

Из третьего уравнения системы (1.11) следует выражение:

2

1

P

B

С

вх

С

K

τk

τCkС

С









После подстановки его значения во второе уравнение системы (1.11) и преоб-

разований получим:

15

 

     

2

2222

1222

1 τkτkKτk

τCkCτkKτCk

С

P

A

B

вхP

C

вх

B







TR

E

jj

j

ekk







0

(1.12)

V

Vr

τ 

На основе полученного решения (1.12) составляется расчетный модуль пря-

мой задачи:

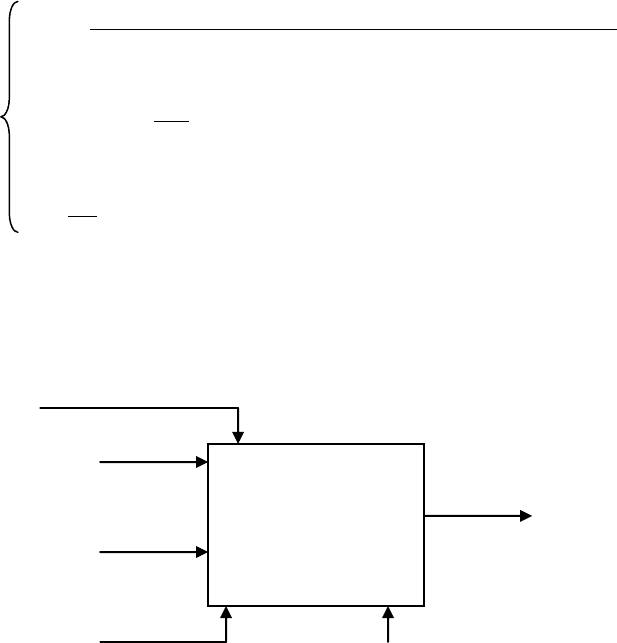
Рис. 3. Расчетный модуль компьютерного решения прямой задачи для примера 2

Пример 3. В лабораторном реакторе идеального перемешивания в стацио-

нарном режиме проводится газофазная гомогенная реакция известного механизма:

ВА

k

2

выхвх

ТТТ 

выхвх

VV 

В смеси присутствует вещество С, не участвующее в реакции.

Заданы:

k

– константа скорости стадии (результат кинетического анализа), с

-1

,

 

C,B,AiС

i

вх



– концентрации компонентов смеси на входе в реактор, моль/м

3

,

вх

V

– объемная скорость входного потока, м

3

/с.

Определить состав смеси на выходе из реактора

 

C,B,AiС

i

вых



и объем-

ную скорость на выходе реактора

вых

V

.

Решение. Тепловой баланс исключается. Основа покомпонентного матери-

ального баланса – уравнение (1.2).

Скорость стадии реакции:

A

Ckr 

1

Модуль

Прямая задача

для примера 2

выхвх

VVV 

321

0

,,j,E,k

jj



C,B,AiC

,iвх



выхвх

TTT 

Vr

C,B,Ai,CC

i

вых



2

Р

К

16

Скорость реакции по компонентам:

1

rR

A



1

2 rR

B



0

C

R

Математическое описание реактора:

0



A

Aвых

A

вхвх

Ck

Vr

СVСV

02 



A

Bвых

B

вхвх

Ck

Vr

СVСV

(1.13)

0



Vr

СVСV

Cвых

C

вхвх

Данная система из трех алгебраических уравнений связывает четыре неиз-

вестные величины

А

С

,

В

С

,

С

,

вых

V

. Уравнение, связывающее

вх

V

и

вых

V

, для

смеси идеальных газов можно вывести из уравнения Менделеева-Клайперона:

TRnVP 

,

где

V

– объем, м

3

;

P

– давление, Па;

n

– количество молей вещества;

T

– темпе-

ратура, К;

R

= 8,314 Дж/(моль · К) – универсальная газовая постоянная.

При

выхвх

ТТТ 

и

constP 

вход в реактор:

вхвхвх

TRsmPV 

выход из реактора:

выхвыхвых

TRsmPV 

TRsm

PV

вх

вых

вх

вых







, (1.14)

где

 

вх

С

вх

В

вх

А

вх

С

вх

В

вх

А

вхвх

VCCCmmmsm 

– входной мольный поток;

 

выхСВА

С

вых

В

вых

А

выхвых

VCCCmmmsm 

– выходной мольный поток.

Математическое описание реактора представлено системой из четырех ал-

гебраических уравнений (1.13) и (1.14), содержащих четыре искомые переменные

А

С

,

В

С

,

С

,

вых

V

. Решение математического описания:

VrkV

VС

С

вых

вх

А

вх

А







вых

Aвх

В

вх

B

V

VrCkVC

C





2

вых

вх

С

вх

С

V

VC

C





(1.15)

17

вх

выхвх

вых

sm

smV

V





Решение уравнений подстановкой невозможно, так как

вых

V

, входящая в пер-

вые три уравнения, зависит от величины

вых

sm

, которая, в свою очередь, определя-

ется концентрациями

А

С

,

В

С

,

С

. Подобные системы можно решать итерацион-

ными методами, идея которых заключается в следующем.

Если алгебраическое уравнение

F(x) = 0 (1.16)

не поддаѐтся прямому решению, то оно преобразуется к виду

x = f(x) (1.17)

так, чтобы производная

 

.x'f 1

Затем задаѐтся начальное приближение

*х

,

оно подставляется в правую часть уравнения (1.17) и рассчитывается новое значе-

ние

**х

. Оно, в свою очередь, подставляется в правую часть уравнения (1.17)

(

**х*х 

) и вновь рассчитывается новое значение

**х

Расчѐты заканчиваются

при их практическом совпадении:

ε

*х

*х**х





.

18

Х*

Х

1

*

Х

2

*

Х

1

**

Х**

0

Х*

Х

1

*

Х

2

*

Х

1

**

Х**

0

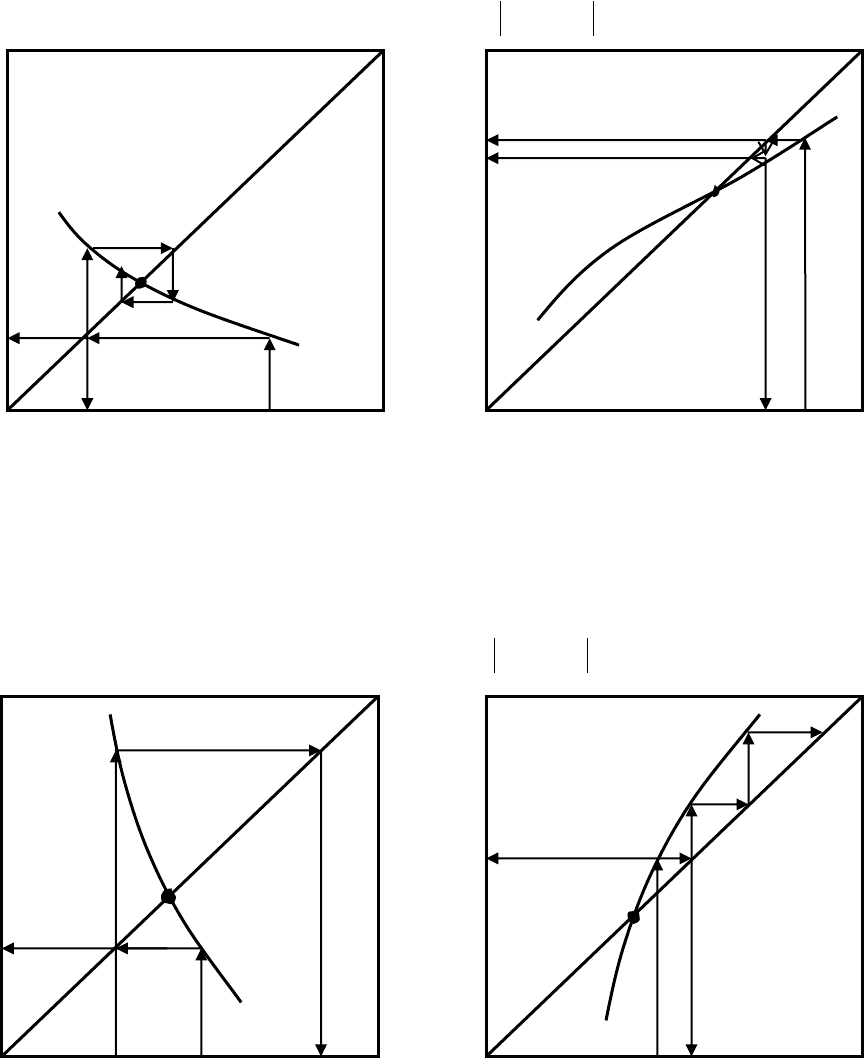
Сходящиеся итерации

 

1*' xf

(*) – точка х

*

=х

**

– решение уравнения F(x)=0

Несходящиеся итерации

 

1*' xf

Рис. 4. Графическая иллюстрация итерационного метода решения

*

Х*

Х

1

*

Х

2

*

Х

1

**

Х**

*

0

Х*

Х

1

*

Х

2

*

Х

1

**

Х**

Х

2

**

*

0

19

1 Преобразование

 

0xF

к форме

 

*xf**x 

2

Да Производная Нет

 

1



*xf

4 3

Задание начальной

*Х

, Преобразование

 

0xF

ε

,

0n

к новой форме

 

*xf**x 

5 Расчет

 

*xf**x 

6

Да

ε

*х

*х**х





Нет

7 Окончание вычисления

х

8

*x**x 

1 nn

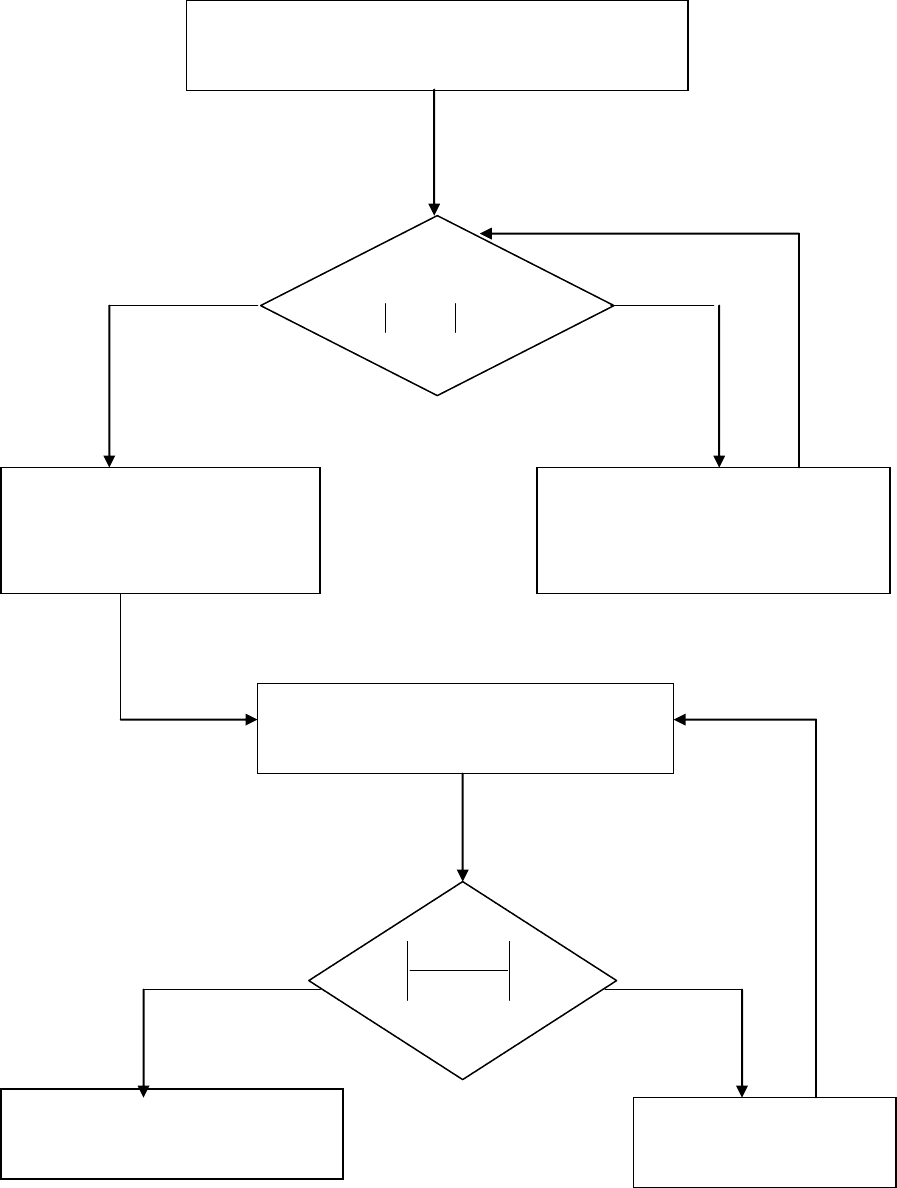
Рис. 5. Итерационное вычисление алгебраического уравнения

 

0xF

:

ε

– малая величина,

n

– счетчик итераций

20

Блоки 1, 2, 3 предназначены для подготовки прямой задачи к компьютерному

решению. Блоки 4, 5, 6, 7, 8 – компьютерное решение алгебраического уравнения

 

0xF

итерационным методом.

Методом итераций можно решать и системы алгебраических уравнений. На-

пример, система из двух алгебраических уравнений

 

0y,xF

 

0y,xG

(1.18)

приводится к виду

 

y,xfx 

 

y,xfy 

(1.19)

так, чтобы производные

 

1



xf

и

 

1



xg

.

Далее задаются начальные приближения

*x

,

*y

. Они подставляются в пра-

вые части уравнений системы (1.19) и рассчитываются новые значения

**x

,

**y

.

Они, в свою очередь, вновь подставляются в правые части (1.19) (

**x*x 

,

**y*y 

) и рассчитываются новые значения

**x

,

**y

. Расчеты продолжаются

до практического совпадения

**x

и

*x

,

**y

и

*y

:

x

εxΔ 

и

y

εyΔ 

. Алгоритм

расчета аналогичен приведенному на рис. 5.

Если задать начальное приближение по

вых

V

, то по уравнениям системы

(1.15) легко определяются

А

С

,

В

С

,

С

и вновь

вых

V

. Следовательно, достаточно

организовать только итерационную процедуру расчета только

вых

V

. Для этого тре-

буется преобразовать

 

0

вых

VF

в

 

выхвых

VfV 

, то есть фактически использо-

вать форму последнего уравнения системы (1.15).

Алгоритм итерационного решения систем алгебраических уравнений (1.15):

1. Исходные данные (условия примера 3 и заданное значение

ε

)

2. Расчет

вх

sm

– пояснение к уравнению (1.14)

3. Начальное приближение

*V

вых

=

вх

V

, число итераций n = 0

4. Расчет

А

С

– уравнение 1 системы (1.15)

5. Расчет

В

С

– уравнение 2 системы (1.15)

Янчуковская Е.В., Ушакова Н.И. Математическое моделирование химических реакторов

Подождите немного. Документ загружается.