Яковлев В.В. Экологическая безопасность, оценка риска

Подождите немного. Документ загружается.

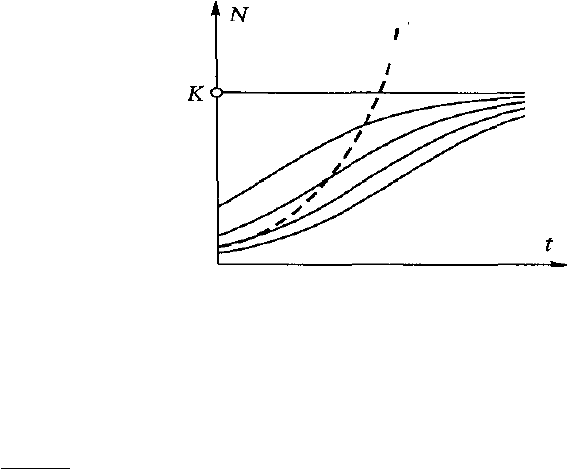
Рис. 5.2.1. Изменение численности логистической популяции.

Различие между этими случаями хорошо видно из рис. 5.2.1. Отме-

тим, что соотношение (5.2.4) описывает, в частности, популяции фрукто-

вых вредителей и некоторых видов бактерий. Пример роста биомассы

дрожжевых клеток в культуре и кривая роста, предсказанная логистиче-

ским уравнением, показан на рис. 5.2.2 .

Отношение (5.2.5) характеризует чувствительность вида к

нехватке

пищи: если дробь

мала, то вид очень чувствителен к нехватке пищи.

Во-вторых, из (5.2.4) следует, что при малых N

и конечном t имеем:

)exp()(

tNtN ⋅⋅=

т. е. в популяции малой численности (когда отсутствует заметное влияние

лимитирующих факторов) кривая изменения численности сходна с кривой

динамики роста (5.1.3) в отсутствие лимитирующих факторов среды.

N(t)

время, ч.

Рис. 5.2.2. Кривая роста биомассы дрожжевых клеток.

Чтобы описать процесс роста населения США, в 20-х годах логисти-

ческую модель предложил Е. Перл (совместно с Ридом). Когда логисти-

ческая формула была опубликована, выяснилось, что ещё в 1838 г. она

предлагалась бельгийским математиком Пьером Франсуа Ферхюльстом

(1804 - 1849) для описания роста народонаселения. Эта простая и на-

глядная модель достаточно хорошо описывает динамику

роста многих

природных популяций. Широкое использование уравнения (5.2.3) связано

с тем, что оно хорошо отражает начальный экспоненциальный рост попу-

ляции и асимптотическое приближение её численности к некоторому ко-

нечному значению, т. е. оно является простейшим дифференциальным

уравнением, которое обладает следующими свойствами (рис. 5.2.3):

- при малых значениях N, пока популяция не исчерпала свои ресурсы

(пищу или пространство), логистическое уравнение (5.2.3) сводится к

уравнению (5.1.1) и возрастание N носит экспоненциальный характер;

- с возрастанием t растет N, ресурсы популяции уменьшаются, рост

постепенно замедляется (фаза отрицательного ускорения), а N постепенно

приближается к постоянному значению К = ε/γ.

Рис. 5.2.3. Логистическая модель с емкостью среды К= ε/γ.

Будем называть обобщенной логистической популяцией

любую по-

пуляцию, локальный закон роста которой описывается уравнением:

))((

)(

tNF

tdN

(5.2.6)

где F(N(t)) удовлетворяет следующим условиям:

а)

,0)())0(( =

KFNF

б)

0))0(( >

′

;

в)

0)(,0))(())0(( >>

′

tNtдляtNFNF

Для многих видов животных, способных мигрировать достаточно

свободно и просторно заселяющих пространство обитания, предположе-

ние, что естественная рождаемость В(N(t)) = сопst не совсем верно, ибо

при малых плотностях размножение определяется скорее вероятностью

встречи брачных партнёров, а не физиологической плодовитостью.

Замечание.

В этом пункте при исследовании динамики численности изолирован-

ных популяций предполагалось, что все особи в популяции одинаковы и на

внешние воздействия они реагируют мгновенно. Однако природные попу-

ляции не могут мгновенно реагировать на внешние воздействия, реакция

на эти воздействия может происходить с некоторым запаздыванием.

Например, у рыб это запаздывание соответствует интервалу между от-

кладыванием икры и достижением потомством репродуктивной зрело-

сти, а рождаемость травоядных даже в идеальных климатических усло-

виях будет зависеть (из-за оскудения пастбищ) не только от текущей

численности, но и от численности в

прошлом, на интервале времени, при-

ближенно равном периоду восстановления пастбища. Запаздывание мо-

жет быть также обусловлено длительным достижением репродуктив-

ного возраста и дискретностью сезонов размножения. Репродуктивные и

другие запаздывания могут существовать одновременно.

Одна из первых математических моделей в биологии, учитывающих

временные запаздывания, была предложена Дж. Эвелином Хатчинсоном

(1903 - 1991), который первым среди

экологов обратил внимание на важ-

ную роль запаздываний для динамики экосистем. Он рассмотрел уравне-

ние:

⎥

⎦

⎤

⎢

⎣

⎡

−⋅

−⋅⋅=

TttN

tdN )()(

1)(

)(

, для Т>0, (5.2.7)

где К — максимально возможная стационарная численность популя-

ции (ёмкость среды).

Популяционная модель (5.2.7) основана на следующих соображе-

ниях: по мере увеличения плотности какого-либо вида доступные ему ре-

сурсы сокращаются; эта ситуация описывается логистическим уравнением

(5.2.3). Однако в реальной экосистеме ресурсы способны к самовозобнов-

лению, поэтому действительный уровень ресурсов,

доступных в любой

момент времени, будет зависеть от плотности ресурсного вида в некото-

рый момент времени (t –Т) в прошлом, где Т - «время развития» вида, слу-

жащего ресурсом. Таким образом, обычное (без запаздывания) логистиче-

ское уравнение (5.2.3) следует заменить уравнением (5.2.7). При наличии

запаздываний численность популяции может колебаться: если Т велико

относительно 1/ε, то

уравнение (5.2.7) приводит к расходящимся колеба-

ниям. Вместе с тем логистические уравнение с Т= 0 всегда даёт устойчивое

неколебательное равновесие.

5.3. Динамика численности популяции в периодической среде.

В п.5.1 решение (5.1.3) уравнения (5.1.1) получено в предположении,

что относительная скорость роста численности N(t) популяции зависит

только от величины ε, характеризующей биологические особенности по-

пуляции, и не зависит от типа среды обитания, т. е.

const

tdN

==⋅

)(

Однако в общем случае относительная скорость роста

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

tdN

)(

характеризующая приспособленность популяции к среде обитания, будет

зависеть не только от биологических особенностей самой популяции, но и

от факторов среды обитания. В экологии принято разделять факторы сре-

ды обитания на факторы, интенсивность действия которых зависит от чис-

ленности популяции, и факторы, не зависящие от этой численности. К

факторам среды, не

зависящим от численности популяции, относятся, на-

пример, метеорологические факторы: температура, химический состав сре-

ды, влажность и т. д.

К факторам, интенсивность действия которых зависит от численно-

сти, относят, например, обеспеченность популяции пищей, светом, водой и

т. д.

Таким образом, количественной мерой относительной скорости рос-

та численности популяции (мерой её приспособленности к

среде обитания)

будет функция вида

),( tNw

и, следовательно, уравнение динамики этого роста будет иметь вид

),(

)(

tNw

tdN

=⋅

(5.3.1)

Рассматривая величину приспособленности популяции

),( tNw как

функцию от её численности N, можно построить классификацию типов за-

висимости приспособленности популяции от её численности. Пусть чис-

ленность популяции, развивающейся в некоторой среде, увеличена в «с»

раз. Что произойдёт с приспособленностью популяции

),( tNw ? Разумеется,

это будет зависеть от целого ряда обстоятельств: от обеспеченности попу-

ляции территорией, пищей и т. п.

Если все компоненты среды присутствуют в достаточном количе-

стве, то увеличение численности не изменит величины приспособлен-

ности, т. е. в этом случае:

),(),( tNwtNcw =⋅

(5.3.2)

Такой тип зависимости приспособленности от численности назы-

вают нейтральным, а популяцию соответственно — нейтральной.

Если в среде отсутствует в достаточном количестве хотя бы одна

компонента, необходимая для жизнедеятельности популяции, то её недос-

таток будет лимитировать рост численности популяции, и тогда для функ-

ции

),( tNw

при с >1 справедливо неравенство:

),(),( tNwtNcw <⋅

(5.3.3)

Такой тип зависимости называют лимитирующим, а популяцию -

лимитированной.

Помимо рассмотренных вариантов, возможна ситуация, когда уве-

личение численности в какие-то промежутки времени повышает при-

способленность популяции. Явления такого рода имеют место, когда всту-

пают в действие так называемые факторы «сотрудничества» особей, со-

ставляющих популяцию при освоении среды обитания. То,

что это прин-

ципиально возможно, доказано экспериментально. В этом случае при с > 1

справедливо неравенство:

),(),( tNwtNcw >⋅

(5.3.4)

Среда с такой величиной приспособленности называется стимули-

рующей.

Для получения дальнейших результатов следует установить явный

вид функции приспособленности

),( tNw , стараясь, чтобы это было по воз-

можности простое выражение, включающее минимальное число парамет-

ров.

Сначала рассмотрим динамику численности популяции в нелими-

тированной нейтральной периодической среде. В этой среде величина при-

способленности

),( tNw от N не зависит и является периодической функци-

ей времени t. Периодический характер изменения условий обитания необ-

ходимо учитывать при описании динамики численности популяций самых

различных видов. Так, в динамике популяций млекопитающих большое

значение имеют сезонные изменения погодных условий, для популяции

насекомых — суточные колебания температуры и освещенности, для по-

пуляций

прибрежных видов это могут быть изменения уровня воды, вы-

званные сменой приливов и отливов.

Пусть Т - период колебаний нелимитированной нейтральной пе-

риодической среды; в такой среде функция приспособленности

),( tNw

имеет вид

)(),,(),( TtTtNwtNw

(5.3.5)

где

)()( tTt

для любых значений t.

Уравнение динамики численности популяции (5.3.1) запишется те-

перь следующим образом:

)(

tdN

=⋅

(5.3.6)

Чтобы исследовать свойства решения уравнения (5.3.6), введём ве-

личину

∫

ττεε

)(

, (5.3.7)

имеющую смысл средней скорости изменения численности популяции за

период Т, и вспомогательную функцию ϕ(t), определив её равенством:

[]

⎟

⎠

⎞

⎜

⎝

⎛

−=

∫

τετεϕ

)(exp)(

(5.3.8)

Покажем, что в силу (5.3.7) функция ϕ(t) периодична и имеет тот же

период Т, что и функция ε(t). Действительно, учитывая, что

cons

[] [] []

()

[]

()

)(exp)(exp)(

exp)(exp)(

)(exp)(exp)(exp)(

tTTttTtTt

dTtdTt

dddTt

tTt

ϕεεϕεεϕ

τεεϕτεεϕ

τετετετετετεϕ

=⋅−⋅⋅=−+⋅−⋅⋅=

⎥

⎦

⎤

⎢

⎣

⎡

⋅−⋅⋅=

⎥

⎦

⎤

⎢

⎣

⎡

−⋅⋅=

⎟

⎠

⎞

⎜

⎝

⎛

−⋅

⎟

⎠

⎞

⎜

⎝

⎛

−=

⎟

⎠

⎞

⎜

⎝

⎛

−=+

∫∫

∫∫∫

Найдём теперь решение уравнения (5.3.6). Проинтегрировав его при

N(0)=N

с последующим потенцированием, получим:

⎥

⎦

⎤

⎢

⎣

⎡

⋅=

∫

dNtN

)(exp)(

ττε

(5.3.9)

где N

- численность популяции в начальный момент времени t = 0.

Из (5.3.9) в силу определения (5.3.8) функции ϕ(t) следует:

[]

()

)(exp)(exp)(

ttNdNtN

ϕετετεε

⋅⋅⋅=

⎭

⎬

⎫

⎩

⎨

⎧

−+⋅=

∫

Т.е. изменение численности популяции в нейтральной периодиче-

ской среде запишется в виде произведения экспоненты с показателем роста

и некоторой положительной периодической функции ϕ(t):

)()exp()(

ttNtN

⋅⋅⋅=

Если

>0, т.е. положительна средняя скорость изменения чис-

ленности (средний показатель роста), то численность популяции растёт

бесконечно, колеблясь около экспоненты с показателем

Если

=0, то численность популяции периодически меняется около

некоторого постоянного уровня.

Если

< 0, то численность популяции стремится к нулю с ростом

времени, колеблясь около убывающей экспоненты.

Отметим, что при

= 0 среднее значение численности популяции N

за рассматриваемый период времени, вообще говоря, не равно N

∫∫

⋅=⋅⋅=

+ TTt

)()(

ττϕττϕ

Отсюда следует, что периодичность изменения среды обитания по-

пуляции приводит не только к колебаниям численности, но в зависимости

от формы этой периодичности может сдвигать средний уровень численно-

сти как в меньшую, так и в большую сторону от её начального значения.

При этом, как уже отмечалось ранее, бесконечный рост численности попу-

ляции не имеет непосредственного биологического смысла, это является

лишь идеализированной моделью реальных процессов, протекающих в по-

пуляции на фазе нелимитируемого роста.

Исследуем популяцию, динамика роста которой описывается логи-

стическим уравнением в нестационарной среде. В этом случае удельная

скорость роста ε и коэффициент лимитирования γ в уравнении (5.2.2) бу-

дут уже не параметрами

, а функциями от t, и уравнение принимает вид:

)()()(

)(

tNtt

tdN

⋅−=⋅

γε

Это уравнение (известное как уравнение Бернулли) относительно

неизвестной функции N(t) может быть записано в виде:

)(

γε

=⋅+

⎟

⎠

⎞

⎜

⎝

⎛

(5.3.10)

Уравнение (5.3.10) будет линейным уравнением относительно неиз-

вестной функции

)(

, и его решение может быть записано в форме:

⎥

⎦

⎤

⎢

⎣

⎡

⎟

⎠

⎞

⎜

⎝

⎛

⋅+⋅

⎥

⎦

⎤

⎢

⎣

⎡

−=

∫∫∫

)(exp)(

)(exp

)(

τθθετγττε

откуда:

∫∫

∫

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅+

⎟

⎠

⎞

⎜

⎝

⎛

⋅=

ddN

NtN

)(exp)(1

)(exp

)(

τθθετγ

ττε

(5.3.11)

Пусть нестационарная среда обитания логистической популяции бу-

дет периодической и Т - период колебаний этой среды, тогда

)()(

),()(

tTt

γγ

при всех значениях t.

В этом случае формула (5.3.11) может быть записана следующим образом:

(

)

()

∫

⋅⋅⋅⋅+

⋅

⋅=

NtN

)(exp)(1

)(exp

)(

ττϕτετγ

(5.3.12)

где ⎯ε - средняя относительная скорость изменения роста популяции

за период T в отсутствие лимитирования, определяемая по формуле (5.3.7),

а ϕ(t) - положительная периодическая функция периода T, определяемая

формулой (5.3.8). Если

> 0, то в нестационарной периодической среде

обитания закон изменения численности логистической популяции с тече-

нием времени стремится к периодической кривой с периодом Т.

Следует заметить, что рассмотренная простая логистическая модель,

описывающая динамику развития не только экологической системы, опас-

на при планировании развития системы в рациональном варианте, т.е. при

оптимизации параметров

системы. Такая «оптимизация» может приводить

к полному уничтожению системы вследствие возникающей из-за оптими-

зации неустойчивости решений.

6. Методы оценки экологического риска [12, 13, 14, 21, 23, 30, 31].

Определение экологического риска дано в разделе 1.

Настоящий раздел посвящен методам, предназначенным для прове-

дения анализа риска объектов, использующих или хранящих пожароопас-

ные, взрывоопасные вещества, а также аварийно опасные химические ве-

щества.

Основное требование к результатам анализа риска связано с необхо-

димостью представления объективной информации о выявлении

и иссле-

довании наиболее опасных аварийных ситуаций, а также разработке реко-

мендаций по предотвращению или снижению опасности для людей и ок-

ружающей природной среды.

Под опасностью понимается ситуация, при которой возможно нане-

сение ущерба здоровью людей или вреда окружающей природной среде.

6.1. Общие положения.

Анализ риска является частью системного

подхода к принятию ре-

шений, процедур, практических мер в решении задач предупреждения про-

мышленной опасности или снижения результатов ее реализации.

Анализ риска – центральное звено в обеспечении безопасности. Оно

определяет меры по контролю возможной промышленной опасности и

снижению ожидаемого ущерба.

Процедура анализа риска – составная часть декларирования безопас-

ности промышленных объектов, экспертизы безопасности

Основная задача анализа риска заключается в том, чтобы дать ответы

на три основных вопроса:

• что плохого может произойти? (Идентификация опасностей);

• как часто это может случаться? (Интенсивность возникновения);

• каковы возможные последствия? (Масштабы ущерба).

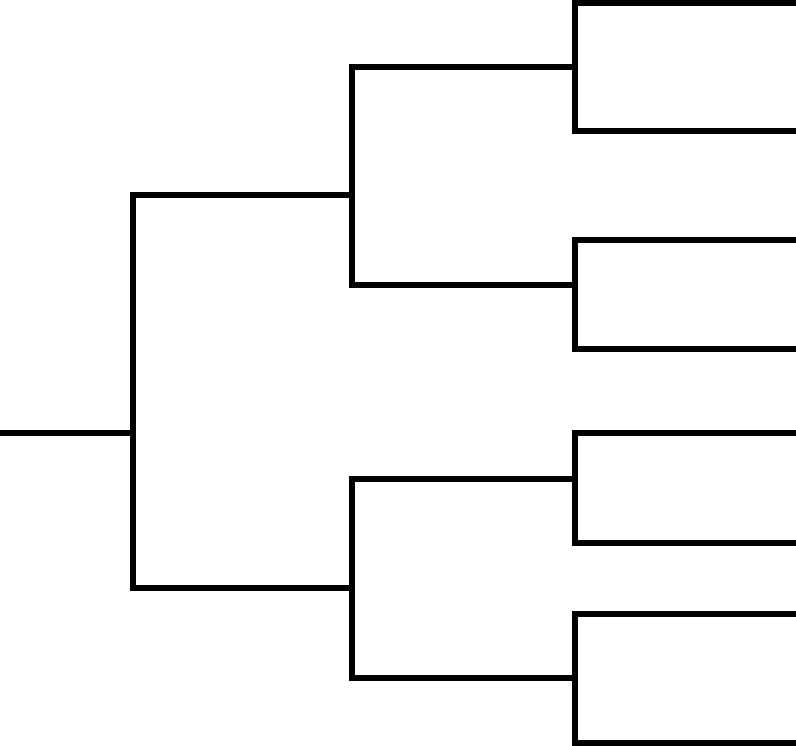
Идентификация опасностей производится, как правило, на основе

анализа «дерева событий», демонстрирующего возможные пути развития

аварийных

процессов.

Пример дерева событий для количественного анализа различных сце-

нариев аварий на установке переработки нефти представлен на рис. 6.1.1.

Цифры рядом с наименованием события показывают условную вероят-

ность возникновения этого события. При этом вероятность возникновения

инициирующего события (выброс нефти из резервуара) принята равной Q.

Значение частоты возникновения отдельного события или сценария пере

считывается путем умножения частоты возникновения инициирующего

события на условную вероятность развития аварии по конкретному сцена-

рию.

ПРЕКРАЩЕНИЕ ГОРЕНИЯ

ИЛИ ЛИКВИДАЦИЯ АВАРИИ

Q⋅0,02

ФАКЕЛЬНОЕ ГОРЕНИЕ

СТРУИ

Q⋅0,04

РАЗРУШЕНИЕ СОСЕДНЕГО

ОБОРУДОВАНИЯ

Q⋅0,02

С МГНОВЕННЫМ

ВОСПЛАМЕНЕНИЕМ

Q⋅0,05

ЭФФЕКТА «ДОМИНО» НЕТ

Q⋅0,001

«ОГНЕННЫЙ ШАР»

Q⋅0,01

РАЗРУШЕНИЕ СОСЕДНЕГО

ОБОРУДОВАНИЯ

Q⋅0,009

ВЫБРОС НЕФТИ

ЛИКВИДАЦИЯ АВАРИИ

Q⋅0,35

НЕТ ВОСПЛАМЕНЕНИЯ

Q⋅0,45

ЗАГРЯЗНЕНИЕ ЗЕМЕЛЬ

БЕЗ МГНОВЕННОГО

ВОСПЛАМЕНЕНИЯ

Q⋅0,10

Q⋅0,95

ПОЖАР ПРОЛИВА

Q⋅0,10

ВОСПЛАМЕНЕНИЕ

НЕФТИ С ЗАДЕРЖКОЙ

Q⋅0,50

ГОРЕНИЕ ИЛИ ВЗРЫВ

ОБЛАКА

Q⋅0,40

Рис. 6.1.1. «Дерево событий» при аварийной ситуацией с разрушени-

ем резервуара хранения нефти.

Результатом идентификации опасностей должен быть перечень со-

бытий, способных привести к аварии, и вероятности их реализации.

Вводятся следующие определения рисков:

• индивидуальный риск – частота поражения отдельного элемента

системы (индивидуума) в результате воздействия исследуемых

факторов опасности;

• коллективный риск

– ожидаемое количество смертельно травми-

рованных в результате возможного воздействия поражающих фак-

торов аварийных ситуаций;

• потенциальный территориальный риск – пространственное рас-

пределение частоты реализации негативного воздействия опреде-

ленного уровня;