Яковлев В.В. Экологическая безопасность, оценка риска
Подождите немного. Документ загружается.

41
Все изменения, внесенные вышеперечисленными законами, направ-
лены на восстановление перечня полномочий субъектов РФ, в том числе
исключенных федеральным законом №122-ФЗ, как за счет собственных
бюджетов, так и за счет субвенций из Федерального бюджета.
Особую роль в вопросах обеспечения экологической безопасности
федеральный закон №199-ФЗ отводит городам федерального значения Мо-
скве
и Санкт-Петербургу. Например, предусматривается, исходя из необ-
ходимости сохранения единства городского хозяйства, полномочия орга-
нов местного самоуправления по вопросам охраны окружающей природ-
ной среды и природопользования определять законами Москвы и Санкт-
Петербурга.
3.3. Законодательство Санкт-Петербурга в области природополь-
зования, охраны окружающей среды и обеспечения экологической
безопасности.
В соответствии
с уставом Санкт-Петербурга нормативно-правовая
база в области природопользования, охраны окружающей среды и обеспе-
чения экологической безопасности включает:
• законы Санкт-Петербурга;
• постановления Законодательного Собрания Санкт-Петербурга;
• постановления губернатора Санкт-Петербурга;
• постановления Правительства Санкт-Петербурга;
• распоряжения исполнительных органов государственной власти.
В Санкт-Петербурге приняты и действуют
следующие законы в об-
ласти охраны окружающей среды и обеспечения экологической безопасно-
сти:
• О защите населения и территорий от чрезвычайных ситуаций при-
родного и техногенного характера, 1996;
• Об экологическом фонде Санкт-Петербурга (с изменениями на 26
июля 2002 года), 1996;
На рассмотрение Законодательного Собрания Санкт-Петербурга в
2004 году представлены проекты законов:
•
О государственных заказниках и памятниках природы Санкт-
Петербурга;
• О разработке месторождений общераспространенных полезных
ископаемых на территории Санкт-Петербурга.
В 2005 году должны быть разработаны проекты законов:
• Об экологическом контроле на территории Санкт-Петербурга и
административной ответственности за экологические правонару-
шения;
• О государственном экологическом мониторинге на территории
Санкт-Петербурга;
42
• Об охране и рациональном использовании недр на территории
Санкт-Петербурга.
3.4. Организация государственного управления в сфере обеспе-
чения экологической безопасности.
Согласно ст. 42 Конституции РФ каждый гражданин имеет право на
благоприятную окружающую среду, достоверную информацию о ее со-
стоянии и на возмещение ущерба, причиненного его здоровью или имуще-
ству экологическим правонарушением
.
Государственные органы в области охраны окружающей природной
среды и регулирования природопользования охватывают три основные на-
правления:
• государственный экологический мониторинг;
• государственная экологическая экспертиза, как форма предупре-
дительного контроля;
• экологический контроль (государственный экологический кон-
троль, муниципальный контроль, производственный экологиче-
ский контроль, общественный экологический контроль).
Государственный экологический мониторинг осуществляется в
соот-
ветствии с законодательством Российской Федерации в целях наблюдения
за состоянием окружающей природной среды, в том числе в районах рас-
положения источников антропогенного воздействия, а также в целях обес-
печения потребностей государства, юридических и физических лиц в дос-
товерной информации, необходимой для предотвращения или уменьшения
неблагоприятных последствий изменения состояния окружающей среды
.
Государственная экологическая экспертиза проводится в целях про-
верки соответствия намечаемой хозяйственной или иной деятельности тре-
бованиям экологического права. Она состоит в проверке содержания пред-
ставляемой на экспертизу проектной документации силами специально
создаваемых экспертных комиссий, состоящих из компетентных специали-
стов, ученых, практиков. Выводом экспертной экологической комиссии
является заключение о допустимости или
недопустимости с позиций эко-
логических требований реализации намечаемой деятельности. Государст-
венной экологической экспертизе подлежат все предплановые, предпро-
ектные и проектные материалы по объектам и мероприятиям, намеченным
к реализации на территории Российской Федерации, независимо от их
стоимости и принадлежности. Финансирование и осуществление работ по
всем проектам должно производиться только при наличии положительного
заключения государственной экологической экспертизы.
Государственный экологический контроль осуществляется инспек-
торским персоналом уполномоченных государственных органов в области
охраны окружающей среды и регулирования природопользования. Долж-
ностные лица (инспектора) органов государственного экологического кон-
43
троля проверяют выполнение планов и мероприятий по обеспечению ох-
раны окружающей среды и рационального использования природных ре-
сурсов, контролируют соблюдение экологического законодательства и
подзаконных нормативных актов, принимаю меры к поддержанию долж-
ного экологического правопорядка, и привлекают нарушителей к ответст-
венности.
3.4.1. Федеральные органы исполнительной власти в области
обеспечения экологической безопасности.
Система
органов, имеющих полномочия в сфере природопользова-
ния, охраны окружающей среды и обеспечения экологической безопасно-
сти на уровне Российской Федерации была реорганизована в 2004 году
Указом Президента РФ от 09.03.04 №314 «О системе и структуре феде-
ральных органов исполнительной власти». Этим Указом установлено, что
в систему федеральных органов исполнительной власти входят федераль-
ные
министерства, федеральные службы и федеральные агентства.
Тем же Указом Президента РФ в сфере природопользования, охраны
окружающей среды и обеспечения экологической безопасности образова-
ны:
• Министерство природных ресурсов Российской Федерации;
• Федеральная служба по экологическому, технологическому и
атомному надзору (Ростехнадзор);
• Федеральная служба по надзору в сфере природопользования (Рос-
природнадзор);
• Федеральное
агентство водных ресурсов;
• Федеральное агентство по недропользованию;
• Федеральное агентство лесного хозяйства.
Федеральная служба по экологическому, технологическому и атом-
ному надзору:
• является компетентным огранном Российской Федерации по Ба-
зельской конвенции о контроле за трансграничной перевозкой опасных от-
ходов и их удалением;
• осуществляет нормативное правовое регулирование по вопросам
взимания платы за негативное воздействие на окружающую среду.
Федеральная служба по экологическому, технологическому и атом-
ному надзору осуществляет свои функции непосредственно и через свои
территориальные органы во взаимодействии с органами исполнительной
власти субъектов Российской Федерации, органами местного самоуправ-
ления и общественными объединениями.
44
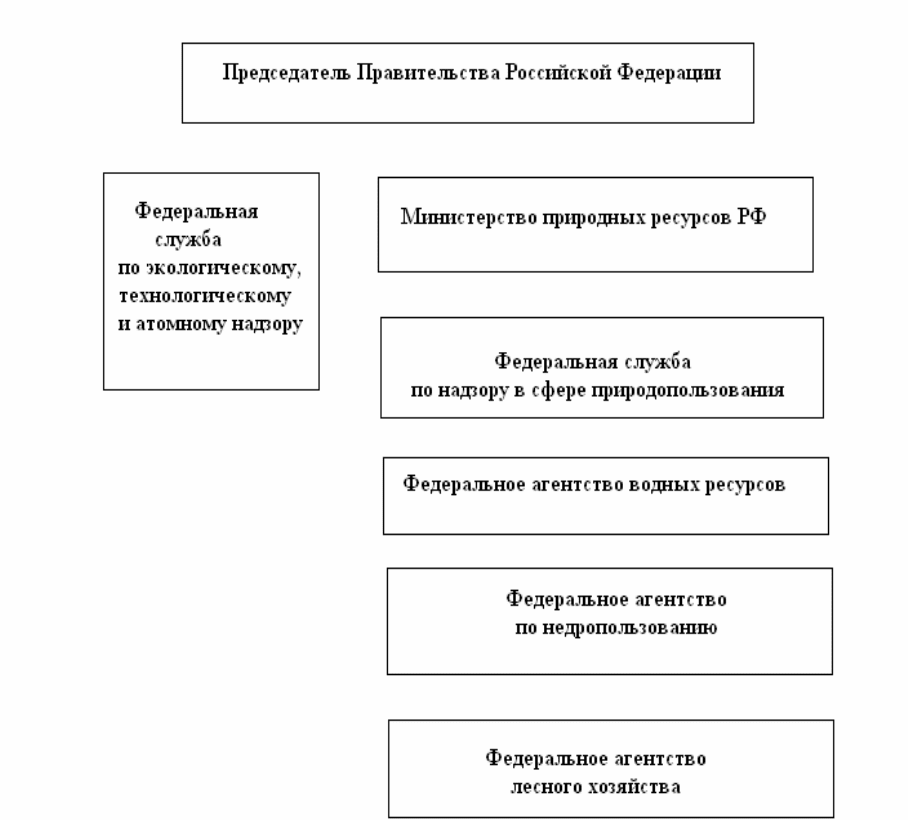
Рис. 3.4.1. Иерархическая система федеральных органов исполни-
тельной власти в сфере природопользования, охраны окружающей среды и
обеспечения экологической безопасности.
Министерство природных ресурсов России (МПР России) осуществ-
ляет функции по выработке государственной политики и нормативно-
правовому регулированию в сфере природопользования, охраны окру-
жающей среды и обеспечения экологической безопасности.
МПР России осуществляет координацию
и контроль деятельности
находящихся в его ведении:
• Федеральной службы по надзору в сфере природопользования
(Росприроднадзор);
• Федерального агентства водных ресурсов;
• Федерального агентства по недропользованию;
• Федерального агентства лесного хозяйства.
45
МПР России вносит в Правительство РФ проекты федеральных за-
конов, нормативных правовых актов Президента Российской Федерации и
Правительства РФ по вопросам, относящимся к сфере ведения Министер-
ства и к сферам ведения подведомственных ему федеральной службы и
федеральных агентств.
Федеральная служба по надзору в сфере природопользования (Рос-
природнадзор) является уполномоченным государственным органом
в об-
ласти экологической экспертизы, федеральным органом исполнительной
власти, осуществляющим государственный контроль в области охраны ок-
ружающей среды (государственный экологический контроль).
Распоряжением Правительства РФ от 30.07.04 №1024-р Федеральной
службе по надзору в сфере природопользования подчинены департаменты
государственного контроля и перспективного развития в сфере природо-
пользования и охраны окружающей среды по
федеральным округам, глав-
ные управления (управления) природных ресурсов и охраны окружающей
среды по субъектам Российской Федерации.
Федеральное агентство водных ресурсов (Росводресурс) является
федеральным органом исполнительной власти, осуществляющим функции
по оказанию государственных услуг и управлению федеральным имущест-
вом в сфере водных ресурсов. Оно, в частности, осуществляет выдачу и
регистрацию лицензий на водопользование
, разработку схем комплексного
использования и охраны водных ресурсов, организацию государственного
мониторинга водных объектов, ведение учета поверхностных и подземных
вод, планирование и утверждение нормативов предельно допустимых
вредных воздействий на водные объекты, согласование нормативов пре-
дельно допустимых сбросов вредных веществ в водные объекты.
Федеральное агентство по недропользованию является федеральным
органом исполнительной власти,
осуществляющим функции по оказанию
государственных услуг и управлению государственным имуществом в сфе-
ре недропользования.
Федеральное агентство по недропользованию осуществляет полно-
мочия собственника в отношении федерального имущества, в том числе
имущества, переданного федеральным унитарным предприятиям, феде-
ральным государственным учреждениям и казенным предприятиям, под-
ведомственным Агентству.
3.4.2. Организация охраны окружающей среды и обеспечения
экологической безопасности в Санкт-Петербурге.
В соответствии с Уставом Санкт-Петербурга Правительство города
составляет систему исполнительных органов государственной власти
Санкт-Петербурга – Администрацию города, структурные подразделения
которой несут ответственность за охрану окружающей природной среды и
обеспечение экологической безопасности.
46
Комитет по природопользованию, охране окружающей среды и обеспече-
нию экологической безопасности:
• осуществляет государственное управление в области охраны ок-
ружающей среды, а также в сфере использования и охраны при-
родных ресурсов;
• осуществляет государственный контроль в области охраны окру-
жающей среды за объектами хозяйственной и иной деятельности,
находящихся на территории
Санкт-Петербурга за исключением
объектов, подлежащих федеральному государственному экологи-
ческому контролю;
• координирует деятельность исполнительных органов государст-
венной власти Санкт-Петербурга, а также подведомственных Ко-
митету государственных унитарных предприятий и учреждений в
сфере природопользования, охраны окружающей среды и обеспе-
чения экологической безопасности.
Комитет по благоустройству и дорожному хозяйству:
• разрабатывает в
установленном порядке концепции развития садо-
во-паркового хозяйства, осуществляет мероприятия по охране и
защите зеленого фонда Санкт-Петербурга;
• осуществляет государственный контроль за состоянием, использо-
ванием, охраной и воспроизводством лесов пригородной лесопар-
ковой зоны Санкт-Петербурга.
Комитет по градостроительству и архитектуре:
• организует разработку и согласование градостроительной доку-
ментации, определяющей
стратегию развития Санкт-Петербурга,
функциональное зонирование города;
• подготавливает предложения по выбору земельных участков для
всех видов градостроительной деятельности.
Комитет по образованию:
• разрабатывает и реализует программы развития дошкольного, об-
щего, начального и среднего профессионального образования, с
учетом социально-экономических, экологических, культурных,
демографических особенностей региона.
Комитет по жилищной политике:
• участвует
в разработке мероприятий по уменьшению количества
твердых коммунальных отходов, их использованию, обезврежива-
нию и размещению;
• контролирует выполнение мероприятий по уменьшению количе-
ства твердых коммунальных отходов и вовлечению их в оборот
как дополнительные источники сырья.
Комитет экономического развития, промышленной политики и торговли:
47
• участвует в разработке мероприятий по организации транспорти-
ровки, обезвреживания и захоронения опасных отходов производ-
ства и потребления.
Комитет по энергетике и инженерному обеспечению:
• обеспечивает устойчивое функционирование и развитие инженер-
но-энергетического комплекса и объектов инженерной инфра-
структуры Санкт-Петербурга;
• осуществляет реализацию государственной политики в сфере
энергетики на территории
Санкт-Петербурга;
• формирует топливно-энергетический запас города, а также лими-
ты потребления топливно-энергетических запасов и воды органи-
зациями бюджетной сферы.
Комитет по земельным ресурсам и землеустройству Санкт-Петербурга:
• осуществляет ведение объектов недвижимости и ведение Государ-
ственного земельного кадастра;
• контролирует использование и охрану земель города, соблюдение
земельного
законодательства;
• производит инвентаризацию и мониторинг земель Санкт-
Петербурга;
• разрабатывает предложения по экономическому зонированию тер-
риторий города и по размерам платы за землю.
Главное Управление по делам гражданской обороны и чрезвычайным си-
туациям Санкт-Петербурга:
• подготавливает и содержит в готовности необходимые силы и
средства для защиты населения и территорий
Санкт-Петербурга от
чрезвычайных ситуаций, обучает и подготавливает население для
защиты и действиям в чрезвычайных ситуациях;
• осуществляет сбор и обмен информацией в области защиты насе-
ления и территорий от чрезвычайных ситуаций, обеспечивает
своевременное оповещение и информирование населения об угро-
зе возникновения чрезвычайной ситуации;
• организует и проводит аварийно-спасательные
и другие виды не-
отложных работ;
• осуществляет контроль и надзор за выполнением мероприятий по
предупреждению чрезвычайных ситуаций и готовностью к дейст-
виям при их возникновении.
В целях повышения эффективности реализации городских экологи-
ческих программ Распоряжением губернатора от 16.02.98 №163-р создан
Координационный совет по проблемам охраны окружающей среды при
Правительстве Санкт
-Петербурга. Председателем Совета назначен вице-
губернатор Санкт-Петербурга Л.А. Косткина.
Решения совета носят рекомендательный характер.

48
4. Простейшие аналитические модели популяционной динамики.
В экологии значение термина «популяция», первоначально обозна-
чавшего группу людей, в настоящее время расширено и обозначает любую
совокупность особей, которые могут скрещиваться между собой и произ-
водить жизнеспособное потомство.
Математические модели развития популяций рассматриваются при
допущении, что основным показателем является численность или плот-
ность
особей. Плотность популяции - это величина популяции, отнесенная
к единице пространства. Её обычно измеряют и выражают числом особей
или биомассой популяции на единицу площади или объема. Например, 300
деревьев на 1 га или 200 кг рыбы на 1 га поверхности водоема [4].
В дальнейшем рассматриваются простейшие модели, описывающие
изменения во времени только общей численности популяции. При по
-
строении этих моделей все особи, составляющие популяцию, считаются
совершенно идентичными, а величина численности принимается исчерпы-
вающей характеристикой популяции как динамической системы. Оказыва-
ется, что даже при таком сравнительно простом описании популяции мож-
но построить модели, хорошо отражающие ряд экспериментальных фак-
тов, касающихся роста или гибели популяций.
Основу решения подобных задач
составляют методы, основанные на
моделях динамики средних и методы исследования логистических моде-
лей.
4.1. Динамика средних [8]
Если в системе, состоящей из N однородных элементов, происходит
марковский случайный процесс, причем известен размеченный граф со-
стояний системы (известны интенсивности λ
ij
всех потоков изменения со-
стояний системы), то для средних численностей состояний можно соста-
вить дифференциальные уравнения, пользуясь следующим мнемониче-
ским правилом (мнемоника, мнемотехника – совокупность приемов,
имеющих целью облегчить запоминание возможно большего числа сведе-
ний, фактов; основана главным образом на законах ассоциации идей; ас-
социация – объединение, союз):
• производная средней численности
состояния равна сумме стольких
слагаемых, сколько стрелок связано с данным состоянием;
• если стрелка направлена из состояния, то слагаемое имеет знак
«минус», если стрелка направлена в состояние, - то знак «плюс»;
• каждое слагаемое равно произведению интенсивности потока со-
бытий, переводящего элемент
по данной стрелке, на среднюю чис-
ленность того состояния, из которого исходит стрелка.
49
Составленные по этому правилу дифференциальные уравнения, в ко-
торых неизвестными функциями являются средние численности элемен-
тов, мы будем называть уравнениями динамики средних.
Пример 4.1.1.
Пусть система состоит из N=100 однородных элементов (техниче-
ских или биологических), каждый из которых
в данный момент времени
может находиться в одном из двух состояний:
S
1
– исправное состояние (трудоспособное, живое);
S
2
– неисправное (больное, ремонтируемое, на излечении).
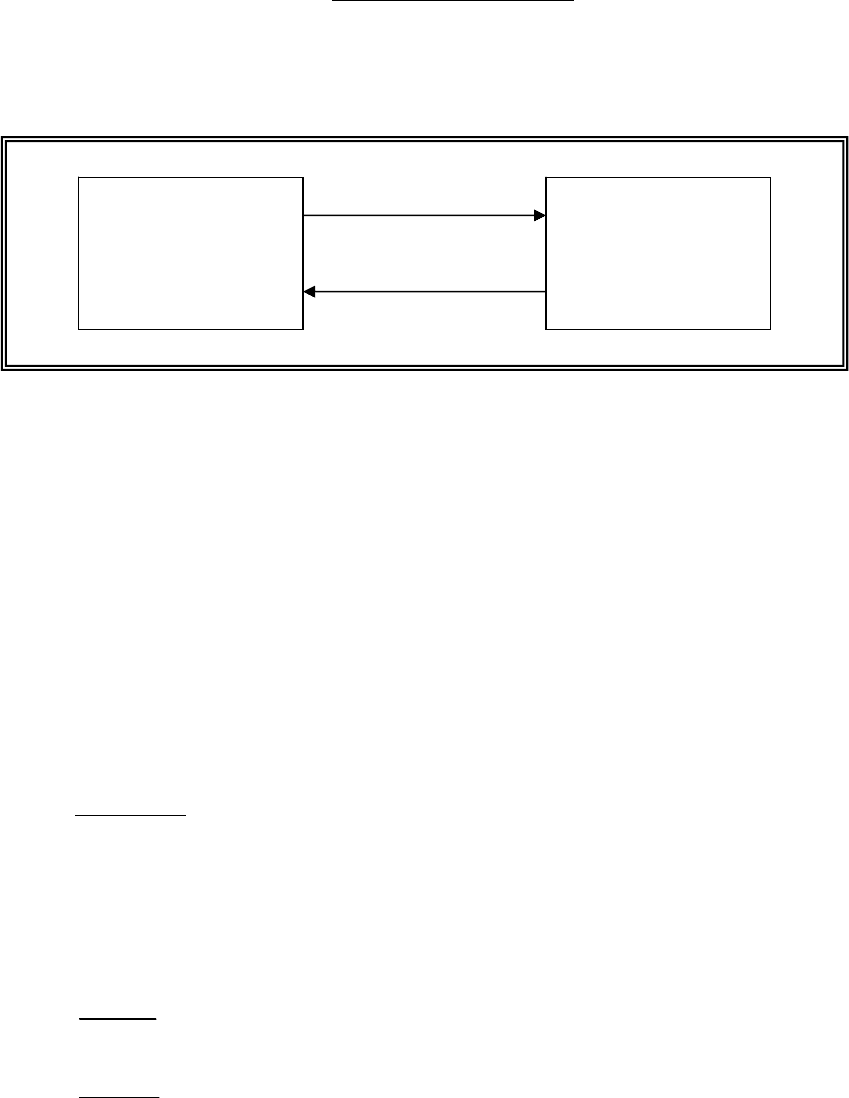
λ
µ
Рис. 4.1.1. Размеченный граф состояний системы.
Переход элемента из состояния S
1
в состояние S
2
происходит под
действием потока отказов λ. Пусть λ = 1.5 (1/год), т.е. в течение трех лет
два элемента перейдут в состояние S
2
.
Среднее время восстановления элемента равно t
P
= 1/µ = 1/3 года (т.е.
четыре месяца), откуда интенсивность восстановления µ = 3.
Необходимо составить уравнения динамики средних для нормально
функционирующей системы и решить ее при условии, что в момент t = 0
все элементы находятся в состоянии S
1
.
В дальнейшем для краткости будем считать элементы в состоянии S
1
– исправные (особи здоровые), а в состоянии S
2
– неисправные (больные).
Решение.
Введем обозначения:
m
1
(t) – среднее значение исправных элементов в момент t;
m
2
(t) – среднее значение неисправных элементов в момент t.
Уравнения для средних численностей состояния элементов будут
иметь вид:
)()(
)(
)()(
)(
tmtm
dt
tdm
tmtm
dt
tdm
12
2
21
1
⋅λ+⋅µ−=
⋅µ+⋅λ−=
(4.1.1)
Вместо двух уравнений можно ограничиться одним, если учесть, что
в любой момент времени t выполняется условие:
S
1
S
2

50
)()( tmNtm
12
−=
(4.1.2)
Подставим уравнение (4.1.2) в первое уравнение системы (4.1.1):
Ntmtm
d
t
tdm
⋅µ+⋅µ−⋅λ−= )()(
)(
11
1
(4.1.3)
или
Ntm
d
t
tdm
⋅µ=⋅µ+λ+ )()(
)(
1
1
(4.1.4)
Уравнение (4.1.4) представляет собой линейное неоднородное диф-
ференциальное уравнение, решение которого построено на методе вариа-
ции произвольной постоянной по алгоритму:
1. Вначале находится общее решение соответствующего одно-
родного уравнения,
2. Предполагается, что произвольная постоянная – это функция
от переменной t, т.е. C=C(t);
3. После подстановки в исходное уравнение
dt
tdm )(
1
и m
1
(t) из по-
лученного дифференциального уравнения определяется иско-
мая функция m
1
(t) при заданных начальных условиях:
m
1
(t) = N при t = 0 (4.1.5)
Составим однородное уравнение для (4.1.4):
0
1
1
=⋅µ+λ+ )()(
)(
tm
d
t
tdm
или, учитывая, что m
1
(t)>0 (в противном случае система не работает):
0
1
1
=⋅µ+λ+ dt
tm
tdm
)(
)(
)(
После интегрирования, получим:
()
0
1
=+⋅µ+
λ
+ Cttm )()(ln
Откуда получаем общее решение исходного дифференциального
уравнения:
[]
tCtm ⋅µ+λ−⋅= )(exp)(
1
(4.1.6)
Полагаем согласно п. 2 алгоритма C = C(t) и дифференцируем (4.1.6):
[] []
ttCt
d
t
tdC
d
t
tdm
⋅µ+λ−⋅µ+λ⋅−⋅µ+λ−⋅= )(exp)()()(exp
)()(
1
(4.1.7)
Подставляем (4.1.6) и (4.1.7) в (4.1.4):
[] [] []
NttCttCt
dt
tdC
⋅=⋅+−⋅⋅++⋅+−⋅+⋅−⋅+−⋅
µµλµλµλµλµλ
)(exp)()()(exp)()()(exp
)(
Или
[]
tN
dt
tdC
⋅µ+λ+⋅⋅µ= )(exp
)(
(4.1.8)
Заметим, что экспонента поменяла знак.
